🍀引言

在当今数据驱动的时代，数据的质量和准确性成为决策的关键因素。然而，由于不同特征之间的度量单位和尺度不同，数据的分布可能会出现偏差，从而影响建模和分析的结果。为了解决这个问题，数据归一化成为优化数据处理的重要技巧。本文将介绍数据归一化的概念、常用方法以及它在机器学习和数据分析中的应用

---

🍀数据归一化的概念

数据归一化（Normalization）是一种常见的数据预处理技术，通过对数据进行数学变换，将其映射到特定的范围内，使得不同特征之间具有可比性。数据归一化的目标是消除数据中的量纲差异，使得数据更容易进行比较和分析。

数据归一化可以分为以下几种常见的方法：

• 最小-最大归一化（Min-Max Normalization）：将数据线性映射到[0, 1]区间，公式如下：
  X_normalized = (X - X_min) / (X_max - X_min)，其中X_min和X_max分别表示数据的最小值和最大值。

• Z-Score归一化（Standardization）：基于数据的均值和标准差进行归一化，公式如下：
  X_normalized = (X - X_mean) / X_std，其中X_mean和X_std分别表示数据的均值和标准差。

• 小数定标归一化（Decimal Scaling）：通过移动小数点的位置进行归一化，公式如下：
  X_normalized = X / (10 ^ j)，其中j是使得数据的绝对值最大的位数。

---

🍀数据归一化的应用

机器学习中的特征缩放
在机器学习算法中，特征缩放是一个重要的预处理步骤。通过对输入特征进行归一化，可以防止某些特征对模型的训练结果产生过大的影响，从而提高模型的性能和稳定性。常见的机器学习算法，如线性回归、逻辑回归和支持向量机等，都受益于数据归一化的应用。

数据可视化和分析
在数据可视化和分析过程中，数据归一化可以帮助我们更好地理解数据的分布和趋势。通过将数据映射到相同的尺度范围内，不同特征之间的关系和变化将更容易观察和解释。例如，在绘制折线图或散点图时，归一化的数据可以更清晰地展示特征之间的关系。

数据聚类和分类
在聚类和分类算法中，数据归一化可以改善模型的收敛速度和准确性。通过使特征之间具有可比性，聚类算法可以更好地识别数据的簇结构，而分类算法则可以更准确地判别样本的类别。

---

🍀数据归一化的注意事项与实践建议

• 选择适当的归一化方法
  在选择数据归一化方法时，需要根据数据类型和具体任务来决定。最小-最大归一化适合处理受限范围的数据，而Z-Score归一化适用于具有正态分布的数据。此外，小数定标归一化对于非常大或非常小的数值范围也很有效。了解数据的特点和需求，选择合适的归一化方法是关键。

• 注意异常值的处理
  在进行数据归一化时，需要注意异常值的存在。异常值可能对归一化后的数据产生较大的影响，因此需要先对异常值进行处理。可以采用删除异常值、替换为均值或使用离群值检测算法进行处理，确保归一化的稳定性和准确性。

• 归一化的顺序和范围
  在多个特征需要进行归一化时，需要考虑归一化的顺序和范围。一般情况下，可以先对连续型的特征进行归一化，再对离散型的特征进行处理。另外，确保所有特征都在相同的范围内（如[0, 1]或[-1, 1]），以避免某个特征对结果的影响过大。

• 考虑归一化的影响
  数据归一化可能改变原始数据的分布，因此需要在使用归一化数据前后进行比较和分析。特别是在进行数据可视化和解释模型结果时，需要注意归一化的影响，并将其纳入考量。

🍀代码演示

本节主要介绍最值归一化和均值方差归一化

首先是最值归一化，在进行代码演示前，我们需要了解一下基本公式

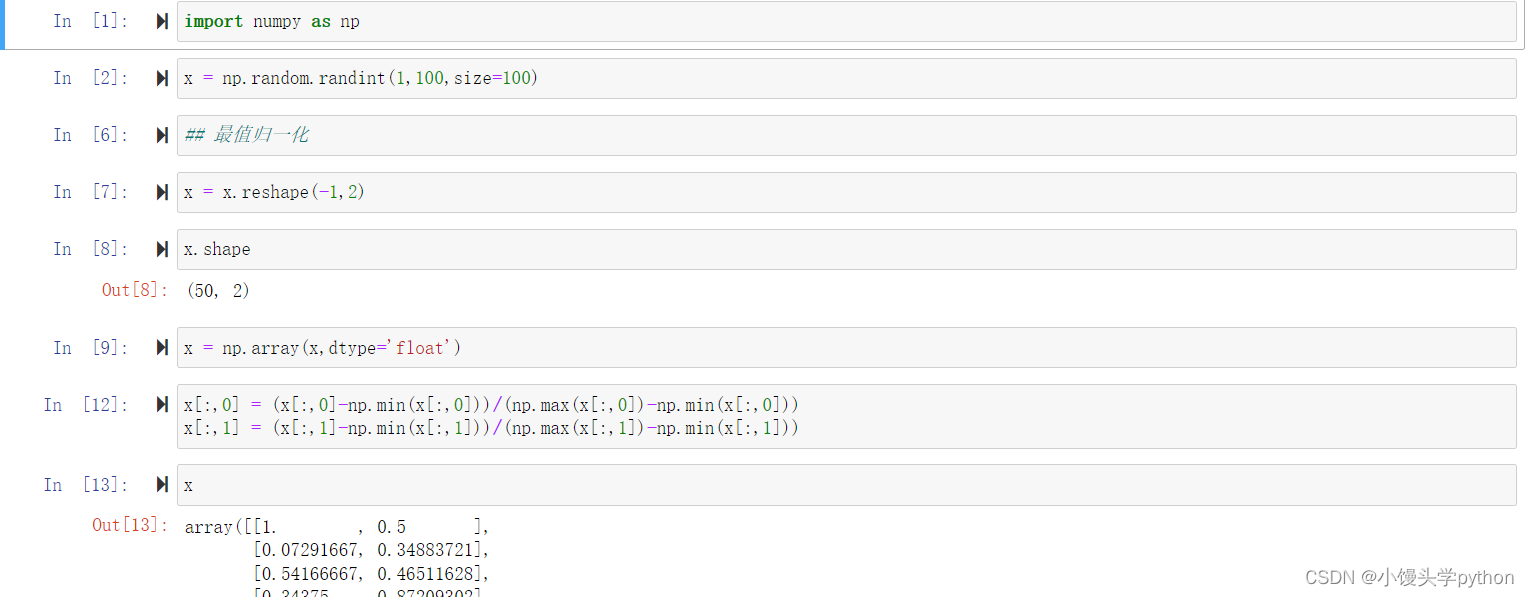
完整代码如下

import numpy as np
x = np.random.randint(1,100,size=100)
x = x.reshape(-1,2)
x = np.array(x,dtype='float')
x[:,0] = (x[:,0]-np.min(x[:,0]))/(np.max(x[:,0])-np.min(x[:,0]))
x[:,1] = (x[:,1]-np.min(x[:,1]))/(np.max(x[:,1])-np.min(x[:,1]))

均值归一化公式如下图

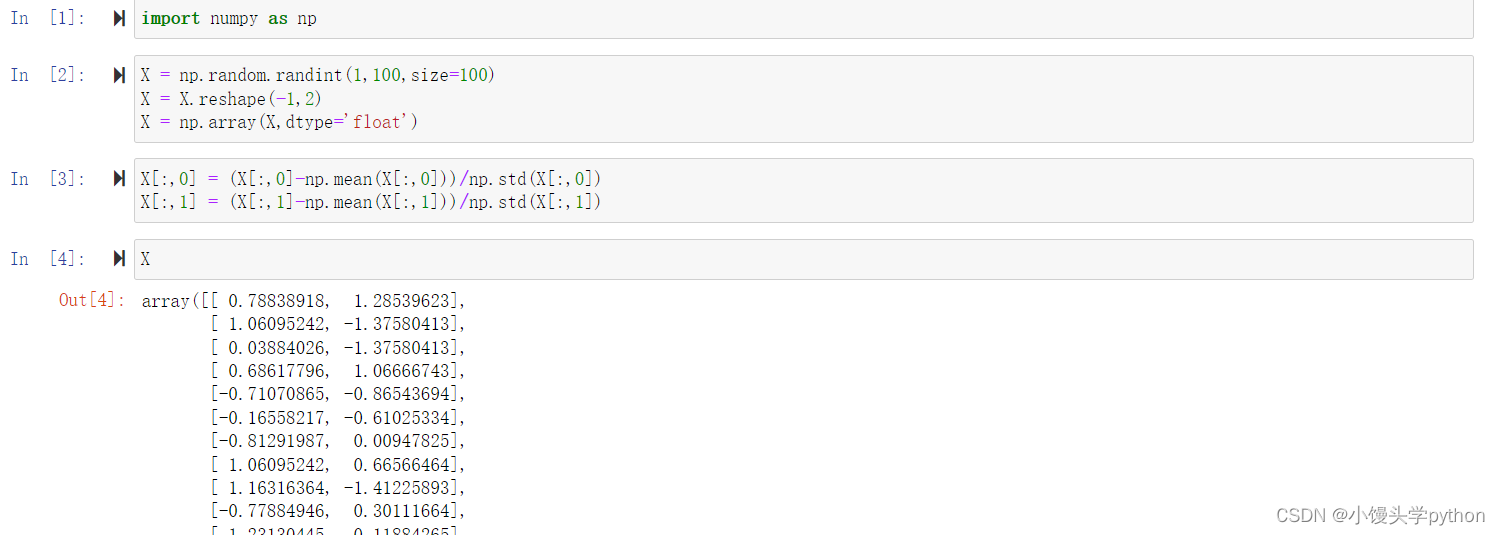
完整代码如下

import numpy as np
X = np.random.randint(1,100,size=100)
X = X.reshape(-1,2)
X = np.array(X,dtype='float')
X[:,0] = (X[:,0]-np.mean(X[:,0]))/np.std(X[:,0])
X[:,1] = (X[:,1]-np.mean(X[:,1]))/np.std(X[:,1])

🍀在sklearn中使用归一化

StandardScaler是用于特征标准化的scikit-learn库中的一个类。通过该类可以对数据进行标准化处理，使得数据的均值为0，方差为1。

在给定的代码中，X1是输入的数据集。fit方法用于计算数据集的均值和标准差，并将其保存为StandardScaler对象的属性。这些统计信息将用于之后的数据转换。

fit方法将根据数据集X1计算并保存均值和方差。之后，你可以使用transform方法将其他数据集进行标准化，使其具有与X1相同的标准化规则。

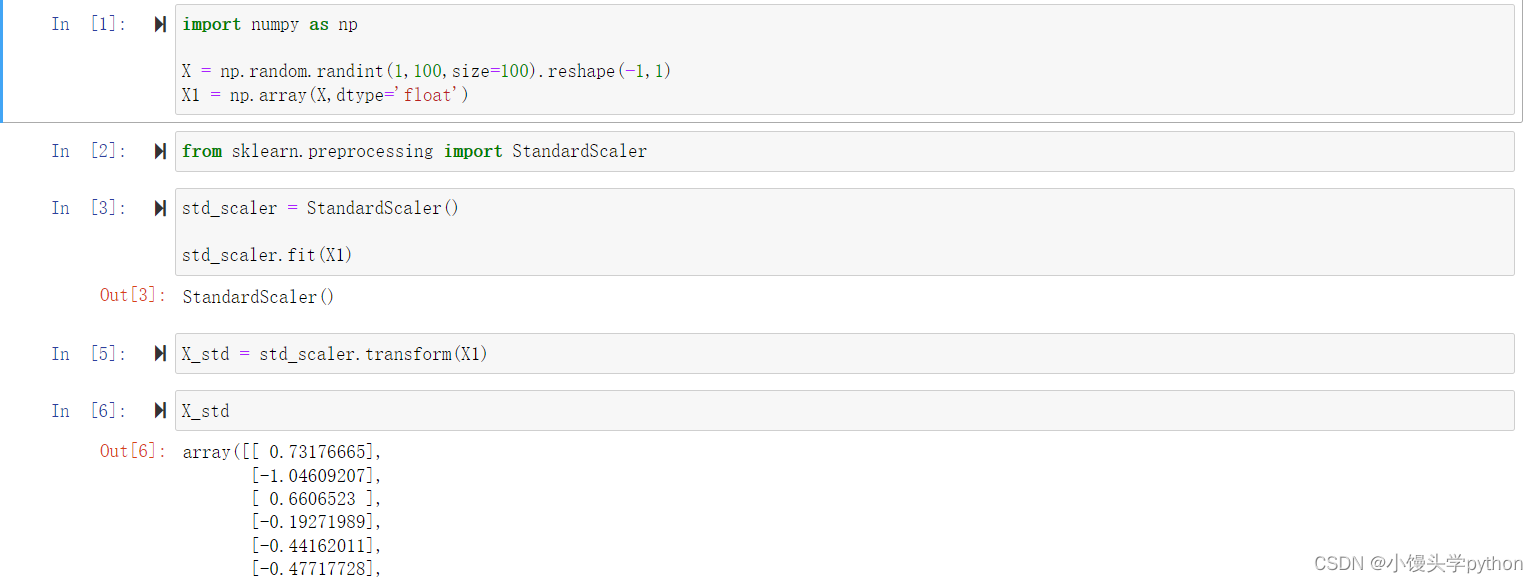
完整代码如下

import numpy as np
X = np.random.randint(1,100,size=100).reshape(-1,1)
X1 = np.array(X,dtype='float')
from sklearn.preprocessing import StandardScaler
std_scaler = StandardScaler()
std_scaler.fit(X1) 
X_std = std_scaler.transform(X1)  

🍀结语

数据归一化是优化数据处理的必备技巧，它使得不同特征之间具有可比性，提高模型的性能和稳定性。在实践中，我们应根据数据类型和任务需求选择合适的归一化方法，并注意处理异常值、归一化顺序和范围，以及考虑归一化的影响。通过合理和正确地应用数据归一化，我们能够充分挖掘数据的潜力，做出更准确和可靠的决策。

挑战与创造都是很痛苦的，但是很充实。