注意：本文只针对离散随机变量做出探讨，连续随机变量的情况不适用于本文探讨的内容！

（一）自信息

1. 自信息

$I(x)=-lo{g}_{n}P(x)$
注意：
若n = 2，叫做bit
若n = 3，叫做tet
若n = e，叫做nat
若n = 10，叫做hat
一般来讲，在信息论中，以2为底数比较普遍。
$$\begin{gathered} 从公式的含义来看， \\ 由于P(x)代表的是概率的大小，其值介于区间(0,1)之间， \\ 当p(x)趋于0时代表信息量是无穷大的；而当p(x)趋于1时，它代表的信息量是0。 \end{gathered}$$

自信息还包括条件自信息和联合自信息。其中条件自信息定义如下：
$$I(xy)=-\log P(x|y)=-\log \frac{p(xy)}{p(y)}$$

联合自信息的定义如下：
$I(xy)=-lo{g}_{n}P(xy)$

联合自信息的特点：
$I(xy)=I(y|x)+I(x)=I(x|y)+I(y)$

当x 与y 相互独立时有：
$I(xy)=I(x)+I(y)$

2. 条件熵
条件熵是平均条件自信息的另一种解释，是条件自信息的期望值。
$$I(x|y)=-\sum _{x\in X}P(x_i|y_i)\sum _{y\in Y}P(y_i)logP(x_i|y_i)=-\sum _{x\in X}\sum _{y\in Y}P(xy)LogP(x|y)$$

要注意：此处log符号前的概率是$p(xy)$而不是$p(x|y)$
另外，从上面的公式可知，必须要计算整个y的条件概率，而不是$y_i$的条件概率，故log符号前面是p(xy)而不是p(x|y)

3. 互信息

$$\begin{gathered} I(x;y)=\sum _{x\in X}\sum _{y\in Y}log\frac{p(xy)}{p(x)p(y)}= \\ \sum _{x\in X}\sum _{y\in Y}log\frac{p(x|y)}{p(x)}=\sum _{x\in X}\sum _{y\in Y}log\frac{p(y|x)}{p(y)}=I(y;x) \end{gathered}$$

互信息的重要性质：

$$I(x;y)=H(x)-H(x|y)=H(y)-H(y|x)$$

证明：
$$\begin{gathered} H(x)-H(x|y)=-\sum _{x\in X}P(x)logP(x)+\sum _{x\in X}\sum _{y\in Y}p(xy)logP(x|y) \\ =-\sum _{x\in X}p(x)logp(x)\sum _{y\in Y}p(y|x)+\sum _{x\in X}\sum _{y\in Y}p(xy)logP(x|y) \\ =-\sum _{x\in X}\sum _{y\in Y}p(xy)logp(x)+\sum _{x\in X}\sum _{y\in Y}p(xy)logP(x|y) \\ =\sum _{x\in X}\sum _{y\in Y}p(xy)log\frac{P(xy)}{P(x)P(y)}=I(x;y) \end{gathered}$$

此处要注意的是一个知识点就是，${\sum }_{y\in Y}p(y_i|x)={\sum }_{y\in Y}\frac{p(x|y_i)p(y_i)}{p(x)}=1$

4.平均互信息

注意平均互信息和互信息的区别。平均互信息即为互信息的期望值，其定义为：
$$\begin{gathered} I(x;y)=\sum _{x\in X}\sum _{y\in Y}P(xy)log\frac{p(xy)}{p(x)p(y)}= \\ \sum _{x\in X}\sum _{y\in Y}P(xy)log\frac{p(x|y)}{p(x)}=\sum _{x\in X}\sum _{y\in Y}P(xy)log\frac{p(y|x)}{p(y)}=I(y;x) \end{gathered}$$

5. 条件互信息
联合集XYZ中，给定条件Z下，X与Y的互信息定义如下：

$$I(x;y|z)=I(x|z)-I(x|yz)=-\log P(x|z)+\log P(x|yz)=\log \frac{p(x|yz)}{p(x|z)}$$

（二）熵

熵的定义比较重要，重点讲述，但是其含义跟上一个标题中的平均互信息、条件熵类似，都是一种期望值。

$$\begin{gathered} 熵的定义：自信息的数学期望为信源的平均自信息量（信息熵）。 \\ 用数学期望值的原因是因为，自信息是一个随机事件的概率,不能用作整个信源的信息测度。 \\ 由此可见，熵是自信息概念的进一步扩展，是自信息的期望值 \end{gathered}$$

二元熵

二元熵是熵的一个特例，也就是一件事情有两种情况发生，这两种情况的概率已知，那么这件事情的熵计算公式如下：
$$H(x)=-plogp-(1-p)log(1-p)$$

离散熵：

$$H(x)=E_x[I(x)]=-\sum _{i=1}^n[P(x_i)lo{g}_{n}P(x_i)]$$

连续熵：

$H(x)=E_x[I(x)]=-{\int }_{+\infty }^{-\infty }P(x)lo{g}_{n}P(x)dx$

注意：积分中是对x微分而不是P(x)

熵的一些重要知识点：
根据极限相关知识，可得：

$$\underset{P(x)\to 0}{\lim }-P(x)lo{g}_{n}P(x)=\underset{x\to 0}{\lim }\frac{lo{g}_{n}P(x)}{\frac{1}{-P(x)}}=\frac{1}{P(x)}P(x{)}^2=P(x)=0$$

同时，当P(x)= 1时，H(x) = 0。

连续熵的导数为0时，$H^{\prime }(x)=-P(x)lo{g}_{n}P(x)=0$，可得：
（1）当熵的导数为0时，可得P(x) = 1( $P(x)=0不在定义域中，不符合条件$），因此熵在该点处取得极值。
（2）再考察P(x) = 1 左右处的值，左侧导数大于0，右侧导数小于0，因此在P(x) = 1处连续熵函数取得最小值0。（$此处似乎有错误,问题在于离散熵和连续熵函数具有很大的区别，其细节问题，留待勘查$）
（3）熵的值总是大于0。由于P(x)的含义是x的概率，概率总是大于0小于1的，又 $-P(x)lo{g}_{n}P(x)=P(x)lo{g}_n\frac{1}{P(x)}$，根据log函数的性质，$lo{g}_n\frac{1}{P(x)}$也大于0，故熵的值必然大于0。
（4）H(xy) = H(x) + H(y|x)
证明：
$$\begin{gathered} H(x)+H(y|x)=-\sum _{i=1}^{n}P(xy)log\frac{P(xy)}{P(x)}-\sum _{i=1}^{n}P(x)logP(x)= \\ -\sum _{i=1}^{n}P(xy)logP(xy)=H(xy) \end{gathered}$$
同理，H(xy) = H(y) + H(x|y)

另外，还有几个重要的结论：
（1）当已知分布上下限时均匀分布的熵最大，当知道均值和方差时正态分布的熵最大。
（2）给定一串数据，其中数据元 x 出现的概率为p(x)，则最佳编码长度为$-lo{g}_{2}P(x)$，整段文本的平均编码长度为$-{\sum }_{i=1}^{n}P(x_i)lo{g}_{2}P(x_i)$，即底为2的熵。
（3）最大离散熵定理：
具有n个符号的离散信源，只有在n个信源等概率的情况下熵才能取得最大值，即等概率的熵最大，这叫做最大离散熵定理。
此定理是熵的判定中一个重要定理。

最大离散熵定理的证明：

$$\begin{gathered} 已知条件： \\ \sum _{i=1}^n{p}_i=1, \\ H(x)=-\sum _{i=1}^n{p}_{i}log{p}_i, \\ {p}_1=p_2=..=p_i=p_n, \\ 根据拉格朗日乘数法则得： \\ H(x)=-\sum _{i=1}^n{p}_{i}log{p}_i+\lambda (\sum _{i=1}^n{p}_i-1)， \\ \frac{\partial H(x)}{\partial p_i}=-nlog{p}_i-n+n\lambda =0,p_i=\frac{1}{n}，由此得知： \\ {p}_i=e^{\lambda -1}，即p_i服从指数分布 \end{gathered}$$

（4）已知均值和方差时，正态分布下熵的值最大，该证明的参考链接如下：
https://zhuanlan.zhihu.com/p/309831227

（5）任何概率分布下的信息熵一定不会大于它对其它概率分布下自信息的数学期望（交叉熵有极小值）
证明：
$$\begin{gathered} \because lnx\le x-1 \\ \therefore \sum _{i=1}^n{p}_i\times ln\frac{q_i}{p_i}\le \sum _{i=n}^n{p}_i\times (\frac{q_i}{p_i}-1)=\sum _{i=1}^n{q}_i-\sum _{i=1}^n{p}_i=0 \\ \therefore \sum _{i=1}^n{p}_i\times ln\frac{q_i}{p_i}=\sum _{i=1}^n{p}_{i}ln{q}_i-\sum _{i=1}^n{p}_{i}ln{p}_i\le 0 \\ \therefore \sum _{i=1}^n{p}_{i}ln{q}_i\le \sum _{i=1}^n{p}_{i}ln{p}_i \end{gathered}$$

交叉熵有极小值也是机器学习的基础理论之一。

（6）熵函数具有上凸性，熵函数必有最大值。（此结论只针对离散随机变量）

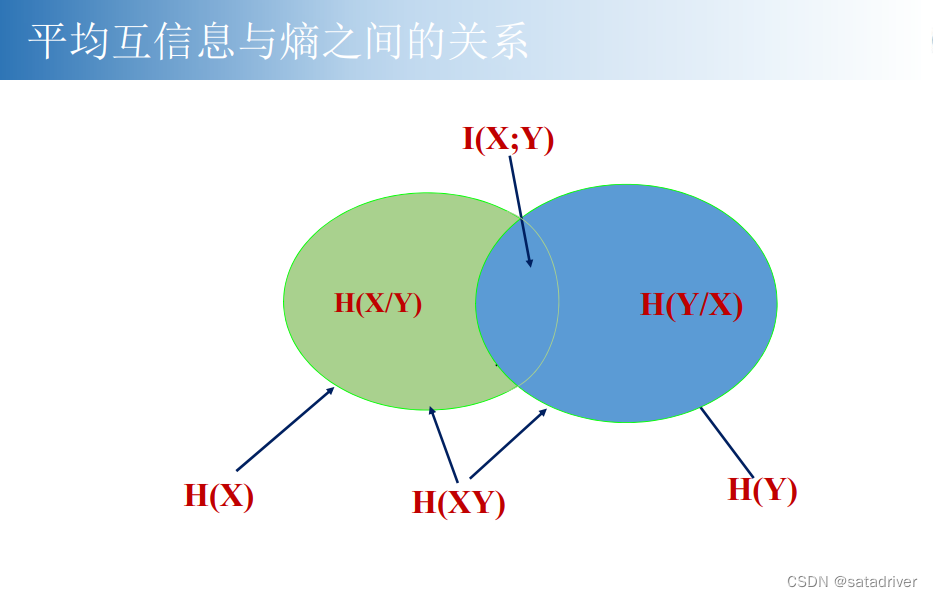
（三）熵几个概念之间的图形化关系

最后，关于信息论中各个部分的关系如下，其中：

图中H(X)与H(Y)是X，Y两个部分的熵，I(XY)是两者熵的重合部分。

H(X|Y)是H(X) 去掉I(XY)部分，H(Y|X)是H(Y) 去掉I(XY)部分，H(XY)是两者的面积去掉I(xy)的部分。