地理测绘基础知识(1) 坐标系经纬度与ECEF直角坐标的基本换算

news2024/11/25 21:34:58

经纬度与ECEF直角坐标的基本换算

我们目前最常用的全球坐标系是WGS-84坐标系，各种手机、地图基本用经纬度来标记位置。然而，经纬度对于空间的计算是很复杂的，需要很多三角函数操作。平面直角坐标系利用向量的运算，可以非常方便的计算角度、距离等参数，在实际应用中往往作为中间计算的工具。

目前用到的很多GIS、遥感与测绘工具里都有这种功能，比如利用 libproj、RTK等工具，直接进行转换。

文章目录

  • 经纬度与ECEF直角坐标的基本换算
    • 1. WGS-84 坐标系
    • 2 从经纬度转换到ECEF
    • 3 从 ECEF 到经纬度
      • (1) 求取经度
      • (2) 纬度、海拔计算
    • 4 代码与工程

1. WGS-84 坐标系

WGS-84 坐标系是目前使用最为广泛的全球坐标系统。其示意图如下：

84
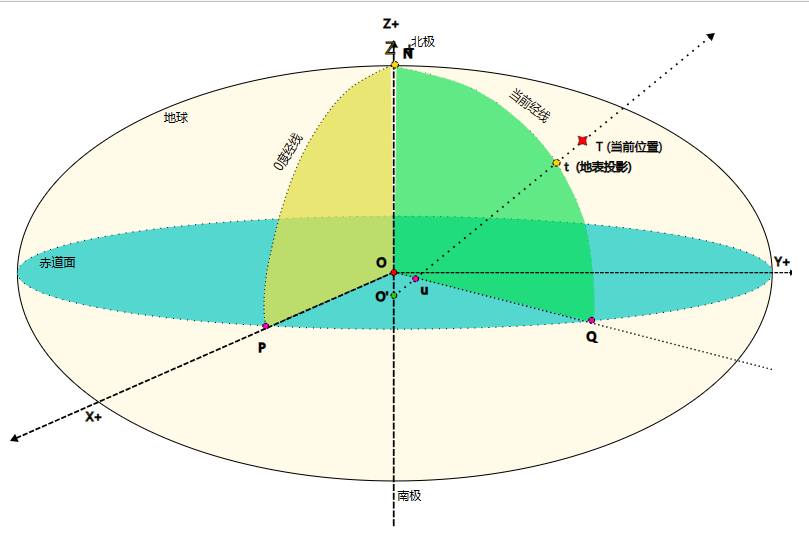
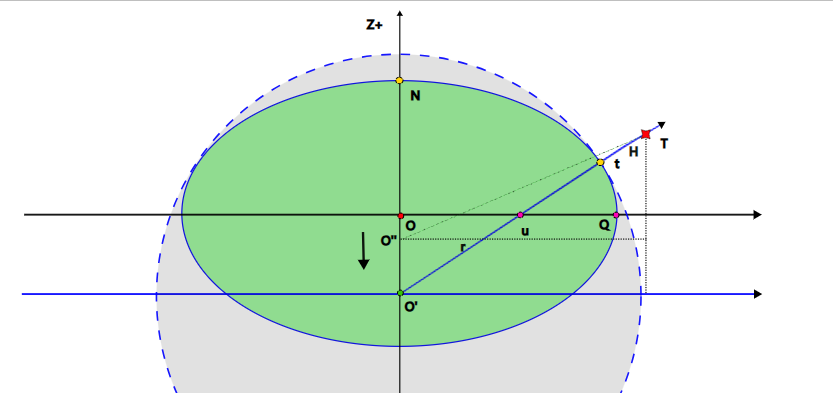
WGS-84坐标系里，地球等效为一个椭圆，直角坐标系原点O位于地球的中心。

  • 坐标轴 Z ⃗ = O N ⃗ \vec{Z} =\vec{ON} Z =ON 指向北极点。
  • 坐标轴 X ⃗ = O P ⃗ \vec{X} =\vec{OP} X =OP 指向格林威治0度经线与赤道面的交点P。
  • 坐标轴 Y ⃗ = X ⃗ ⊗ Z ⃗ \vec Y=\vec X\otimes \vec Z Y =X ⊗Z 呈右手螺旋关系。

当前位置 T 的经纬度定义：

从高度 H 开始定义：

  • T是一个距离参考海平面（椭球面）高度为 H ⃗ = t T ⃗ \vec{H} =\vec{tT} H =tT 的点。
  • t是点T在椭球面上的正射投影，矢量 t T ⃗ \vec{tT} tT 是椭球面上t点切面的法向量。
  • 需要注意的是，和正球面不同，法向量 t T ⃗ \vec{tT} tT 的反向延长线与Z轴的交点是 O’，和原点O并不重合。

对于经度 θ \theta θ 的定义，是这样的：

  • 0度经度大圆 N O P ⌢ \stackrel\frown{NOP} NOP⌢​是由北极点 N, 地心 O, 格林威治经线与赤道面的交点 P 组成的平面。
  • 当前经度大圆 N O ′ T ⌢ \stackrel\frown{NO'T} NO′T⌢是由北极点 N, 交点O’, 当前位置T组成的平面。
  • O、 O’ 、t、 T 都在当前经度面上，直线 O’T 与赤道面的交点为u，矢量 O u ⃗ \vec{Ou} Ou 与赤道的交点是Q。
  • O’、u、t、T四点共线。
  • 经度 θ = ∡ P O Q \theta=\measuredangle {POQ} θ=∡POQ

对于纬度 φ \varphi φ 的定义，是这样的：

  • 椭球的切平面的法线与Z的交点 O’ 和原点并不重合。
  • 纬度定义为法向量 u T ⃗ \vec{uT} uT 与赤道面的夹角。在北半球为正，南半球为负
  • 纬度 φ = ∡ T u Q = ∡ O u O ′ \varphi=\measuredangle {TuQ}=\measuredangle {OuO'} φ=∡TuQ=∡OuO′

2 从经纬度转换到ECEF

  • ECEF 坐标系有利于利用矢量计算简化角度、距离的求取。

已知:

  • 赤道半径 a = 6378137 米，对应上图 O P ⃗ \vec{OP} OP 的长度;
  • 椭球扁率 f = ( a − b ) / a f = (a-b)/a f=(a−b)/a= 1.0/298.257223563。扁率就是衡量椭球是不是很“扁”，正球的扁率为0.
  • 椭球偏心率 e = a 2 − b 2 / a e={\sqrt {a^2-b^2} }/{a} e=a2−b2 ​/a= 0.0818191908426
  • e和f的关系为 e 2 = f ( 2 − f ) e^2=f(2-f) e2=f(2−f)
  • 极地半径 b = 6356752.3142 米，对应上图 O N ⃗ \vec{ON} ON 的长度;

设：经度 θ \theta θ， 纬度 φ \varphi φ， 海拔 H，则有：

r = ∣ R ⃗ ∣ = ∣ O ′ t ⃗ ∣ = a 1 − e 2 sin ⁡ 2 φ = a 1 − f ( 2 − f ) sin ⁡ 2 φ r = \left | \vec R\right |=\left | \vec{O't} \right | = \frac{ a}{\sqrt{1-e^2 \sin^2\varphi }} =\frac{ a}{\sqrt{1-f(2-f) \sin^2\varphi }} r= ​R ​= ​O′t ​=1−e2sin2φ ​a​=1−f(2−f)sin2φ ​a​

经纬度极坐标可以利用矢量 R ⃗ \vec R R 构造一个Z轴平移了的正球，进行极坐标运算。这个正球的球心是 O’。由于x,y没有平移，故而两个坐标系的x、y是重合的。Z坐标z’与z的关系是平移，平移量为OO’的长度：

∣ O O ′ ⃗ ∣ = r e 2 sin ⁡ φ \left | \vec {OO'} \right | = re^2\sin \varphi ​OO′ ​=re2sinφ

下图是把经度大圆 N O Q ⌢ \stackrel\frown {NOQ} NOQ⌢​切割出来，观察：

SP

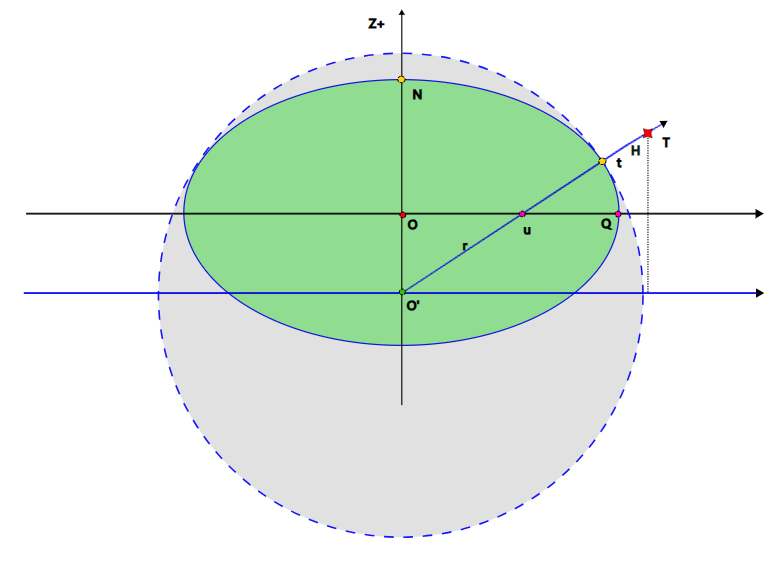
在正球模型下，根据极坐标的基本定义，可以直接计算x,y:

x = ( r + H ) ⋅ cos ⁡ φ ⋅ c o s θ x=\left ( r + H \right ) \cdot \cos \varphi \cdot cos \theta x=(r+H)⋅cosφ⋅cosθ

y = ( r + H ) ⋅ cos ⁡ φ ⋅ s i n θ y=\left ( r + H \right ) \cdot \cos \varphi \cdot sin \theta y=(r+H)⋅cosφ⋅sinθ

Z的坐标，要先计算后，再平移即可得到:

z ′ = ( r + H ) ⋅ s i n φ z'=\left ( r + H \right ) \cdot sin \varphi z′=(r+H)⋅sinφ
z = z ′ − r e 2 sin ⁡ φ z=z' - re^2\sin \varphi z=z′−re2sinφ

带入后，可写成如下等效形式：

z = ( r ( 1 − e 2 ) + H ) sin ⁡ φ z=(r(1-e^2)+H) \sin \varphi z=(r(1−e2)+H)sinφ
z = ( r ( 1 − f ( 2 − f ) ) + H ) sin ⁡ φ = ( r ( 1 − f ) 2 + H ) sin ⁡ φ z=(r(1-f(2-f))+H) \sin \varphi =(r(1-f)^2+H) \sin \varphi z=(r(1−f(2−f))+H)sinφ=(r(1−f)2+H)sinφ

含有扁率的化简，是基于扁率 f = ( a − b ) / a = 1 − b / a f = (a-b)/a = 1 - b/a f=(a−b)/a=1−b/a 计算得到的。

通过上面的处理，极坐标的 T ( θ , φ , H ) T(\theta, \varphi,H) T(θ,φ,H) 便转换为平面直角坐标 T ( x , y , z ) T(x,y,z) T(x,y,z) 。

3 从 ECEF 到经纬度

对上述计算过程而言，逆向运算可以立刻得到经度，却不能解析得到纬度。纬度需要进行迭代。

主要原因是：

∣ O O ′ ⃗ ∣ = r e 2 sin ⁡ φ \left | \vec {OO'} \right | = re^2\sin \varphi ​OO′ ​=re2sinφ

的具体取值不知道导致的。

(1) 求取经度

由于

x / y = tan ⁡ θ x/y=\tan \theta x/y=tanθ

故而

θ = tan ⁡ − 1 ( x / y ) \theta=\tan^{-1} (x/y) θ=tan−1(x/y)

注意处理好象限问题，即可得到经度。

(2) 纬度、海拔计算

对于纬度，则比较复杂。求解三角方程

( r + H ) sin ⁡ φ = z + ∣ O O ′ ⃗ ∣ (r + H) \sin \varphi = z + \left | \vec {OO'} \right | (r+H)sinφ=z+ ​OO′ ​

由于 H 不知道，r 也不知道，加入第二条件（相切，H向量与r共线）后，得到的是二元四次三角方程，很难解析求取。

可以首先假设 ∣ O O ′ ⃗ ∣ = 0 \left | \vec {OO'} \right | =0 ​OO′ ​=0, 求取一个粗略的纬度，并得到 d，利用d反过来更新其他数值，进行迭代。这种迭代收敛的前提，是因为每次计算出的纬度一定小于真实的纬度，这是由三角关系决定的。

CALC迭代的效果是不断地把原点向真实的原点移动，直到z达到一个很小的误差。迭代方法：

设起始偏移 d = ∣ O O ′ ⃗ ∣ = 0 d = \left | \vec {OO'} \right | =0 d= ​OO′ ​=0，迭代开始：

R ′ = r + H = x 2 + y 2 + ( z + d ) 2 R'=r+H = \sqrt{x^2+y^2+(z+d)^2} R′=r+H=x2+y2+(z+d)2 ​

φ ′ = sin ⁡ − 1 z + d R ′ \varphi' = \sin^{-1} {\frac {z+d}{R'}} φ′=sin−1R′z+d​

r ′ = a 1 − e 2 sin ⁡ 2 φ ′ r' = \frac{ a}{\sqrt{1-e^2 \sin^2\varphi' }} r′=1−e2sin2φ′ ​a​

d ′ = r ′ e 2 sin ⁡ φ ′ d'= r'e^2\sin \varphi' d′=r′e2sinφ′

z ′ = R ′ s i n φ ′ − d ′ z'=R'sin \varphi'-d' z′=R′sinφ′−d′

d = d ′ d = d' d=d′

当
e r r = ∣ z − z ′ ∣ < ε err = \left | z-z' \right | < \varepsilon err=∣z−z′∣<ε
时停止迭代。此时

φ = sin ⁡ − 1 z + d x 2 + y 2 + ( z + d ) 2 \varphi = \sin^{-1} {\frac {z+d}{\sqrt{x^2+y^2+(z+d)^2}}} φ=sin−1x2+y2+(z+d)2 ​z+d​

H = R ′ − r ′ H= R'-r' H=R′−r′

4 代码与工程

代码与工程参考

https://gitcode.net/coloreaglestdio/geocalc/-/blob/master/geocalc.h

核心转换逻辑如下：

/*!
 * GEOCalc 实现了基本的WGS-84坐标系的计算。
 * by CEStdio
 * 1997-2023
 *
*/
#include <cassert>
#include <cmath>
namespace CES_GEOCALC {

inline const double a = 6378137;
inline const double pi = 3.14159265358979323846;
inline const double f = 1.0 / 298.257223563;
inline const double e = sqrt(f * (2 - f));
inline const double es = f * (2 - f);
inline const double deg2rad = pi / 180.0;
inline const double rad2deg = 180.0 / pi;

/*!
 * \brief lla2ecef 经纬度坐标到ECEF，
 * \param lla  纬经高(默认)/经纬高, 量纲是度(默认)/弧度、米
 * \param ecef xyz，量纲是米
 * \param rad  角度量纲开关，false 是度，true 是弧度
 * \param latfirst 经纬度顺序，false 是经度\纬度\高度，true 是纬度\经度\高度
*/
inline void lla2ecef(const double lla[/*3*/],
					 double ecef[/*3*/],
					 const bool rad = false,
					 const bool latfirst = true)
{
	const double lat = latfirst ? (rad ? (lla[0]) : (lla[0] * deg2rad))
								: (rad ? (lla[1]) : (lla[1] * deg2rad));
	const double lon = latfirst ? (rad ? (lla[1]) : (lla[1] * deg2rad))
								: (rad ? (lla[0]) : (lla[0] * deg2rad));
	const double H = lla[2];
	const double r = a / sqrt(1 - es * sin(lat) * sin(lat));
	const double d = r * es * sin(lat);
	ecef[0] = (r + H) * cos(lat) * cos(lon);
	ecef[1] = (r + H) * cos(lat) * sin(lon);
	ecef[2] = (r + H) * sin(lat) - d;
}

/*!
 * \brief ecef2lla ECEF到经纬度坐标
 * \param ecef xyz，量纲是米
 * \param lla  纬经高(默认)/经纬高, 量纲是度(默认)/弧度、米
 * \param maxiter  最大迭代次数
 * \param piter  迭代次数输出，可以为null
 * \param eps  Z误差门限
 * \param rad  角度量纲开关，false 是度，true 是弧度
 * \param latfirst 经纬度顺序，false 是经度\纬度\高度，true 是纬度\经度\高度
 * \return 迭代收敛标志
*/
inline bool ecef2lla(const double ecef[/*3*/],
					 double lla[/*3*/],
					 const int maxiter = 32,
					 int * piter = nullptr,
					 const double eps = 1e-10,
					 const bool rad = false,
					 const bool latfirst = true)
{
	const double x = ecef[0], y = ecef[1], z = ecef[2] < 0 ? -ecef[2] : ecef[2];
	const int south = ecef[2] < 0 ? -1 : 1;
	double d = 0;
	double err = 0;
	int iter = 0;
	double Rp = 0, sinphi = 0, rp = 0, dp = 0, zp = 0;
	do {
		Rp = sqrt(x * x + y * y + (z + d) * (z + d));
		sinphi = (z + d) / Rp;
		rp = a / sqrt(1 - es * sinphi * sinphi);
		dp = rp * es * sinphi;
		zp = Rp * sinphi - dp;
		d = dp;
		assert(z >= zp);
		err = z - zp; //z always > zp
		++iter;
	} while (err > eps && iter < maxiter);

	const double lat = asin(sinphi) * south;
	const double lon = atan2(y, x);
	const double H = Rp - rp;

	lla[latfirst?0:1] = lat * (rad?1:rad2deg);
	lla[latfirst?1:0] = lon * (rad?1:rad2deg);
	lla[2] = H;

	if (piter)
		*piter = iter;

	return err <= eps;
}

}; // namespace CES_GEOCALC

对各种边界和迭代次数进行测试, 以确定迭代的收敛性:

using namespace CES_GEOCALC;
	for (double lon = -180; lon <=180; lon+=60)
	{
		for (double lat = -90; lat <=90; lat += 15)
		{
			double LLA[] = {lat,lon,10000};
			double ECEF[] = {0, 0, 0};
			double LLA2[] = {0, 0, 0};
			lla2ecef(LLA, ECEF);
			int iter = 0;
			ecef2lla(ECEF,LLA2,32,&iter);
			printf("LAT=%12.7lf,LON=%12.7lf,dLAT=%10.7lf,dLON=%10.7lf,dALT=%5.3lf, iter = %d\n",
				   lat,lon,
				   LLA[0]-LLA2[0], LLA[1]-LLA2[1], LLA[2]-LLA2[2],iter);
		}
	}

输出：

LAT= -90.0000000,LON=-180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -75.0000000,LON=-180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -60.0000000,LON=-180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -45.0000000,LON=-180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT= -30.0000000,LON=-180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT= -15.0000000,LON=-180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=   0.0000000,LON=-180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 1
LAT=  15.0000000,LON=-180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  30.0000000,LON=-180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  45.0000000,LON=-180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT=  60.0000000,LON=-180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  75.0000000,LON=-180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  90.0000000,LON=-180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -90.0000000,LON=-120.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 2
LAT= -75.0000000,LON=-120.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 6
LAT= -60.0000000,LON=-120.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 6
LAT= -45.0000000,LON=-120.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 7
LAT= -30.0000000,LON=-120.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 8
LAT= -15.0000000,LON=-120.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 8
LAT=   0.0000000,LON=-120.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 1
LAT=  15.0000000,LON=-120.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 8
LAT=  30.0000000,LON=-120.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 8
LAT=  45.0000000,LON=-120.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 7
LAT=  60.0000000,LON=-120.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 6
LAT=  75.0000000,LON=-120.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 6
LAT=  90.0000000,LON=-120.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 2
LAT= -90.0000000,LON= -60.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 2
LAT= -75.0000000,LON= -60.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 6
LAT= -60.0000000,LON= -60.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 6
LAT= -45.0000000,LON= -60.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 7
LAT= -30.0000000,LON= -60.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 8
LAT= -15.0000000,LON= -60.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 8
LAT=   0.0000000,LON= -60.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 1
LAT=  15.0000000,LON= -60.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 8
LAT=  30.0000000,LON= -60.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 8
LAT=  45.0000000,LON= -60.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 7
LAT=  60.0000000,LON= -60.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 6
LAT=  75.0000000,LON= -60.0000000,dLAT=-0.0000000,dLON=-0.0000000,dALT=0.000, iter = 6
LAT=  90.0000000,LON= -60.0000000,dLAT= 0.0000000,dLON=-0.0000000,dALT=0.000, iter = 2
LAT= -90.0000000,LON=   0.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -75.0000000,LON=   0.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -60.0000000,LON=   0.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -45.0000000,LON=   0.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT= -30.0000000,LON=   0.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT= -15.0000000,LON=   0.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=   0.0000000,LON=   0.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 1
LAT=  15.0000000,LON=   0.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  30.0000000,LON=   0.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  45.0000000,LON=   0.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT=  60.0000000,LON=   0.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  75.0000000,LON=   0.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  90.0000000,LON=   0.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -90.0000000,LON=  60.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -75.0000000,LON=  60.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -60.0000000,LON=  60.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -45.0000000,LON=  60.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT= -30.0000000,LON=  60.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT= -15.0000000,LON=  60.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=   0.0000000,LON=  60.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 1
LAT=  15.0000000,LON=  60.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  30.0000000,LON=  60.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  45.0000000,LON=  60.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT=  60.0000000,LON=  60.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  75.0000000,LON=  60.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  90.0000000,LON=  60.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -90.0000000,LON= 120.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -75.0000000,LON= 120.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -60.0000000,LON= 120.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -45.0000000,LON= 120.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT= -30.0000000,LON= 120.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT= -15.0000000,LON= 120.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=   0.0000000,LON= 120.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 1
LAT=  15.0000000,LON= 120.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  30.0000000,LON= 120.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  45.0000000,LON= 120.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT=  60.0000000,LON= 120.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  75.0000000,LON= 120.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  90.0000000,LON= 120.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -90.0000000,LON= 180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2
LAT= -75.0000000,LON= 180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -60.0000000,LON= 180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT= -45.0000000,LON= 180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT= -30.0000000,LON= 180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT= -15.0000000,LON= 180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=   0.0000000,LON= 180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 1
LAT=  15.0000000,LON= 180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  30.0000000,LON= 180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 8
LAT=  45.0000000,LON= 180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 7
LAT=  60.0000000,LON= 180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  75.0000000,LON= 180.0000000,dLAT=-0.0000000,dLON= 0.0000000,dALT=0.000, iter = 6
LAT=  90.0000000,LON= 180.0000000,dLAT= 0.0000000,dLON= 0.0000000,dALT=0.000, iter = 2

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/865320.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【24择校指南】北方工业大学计算机考研考情分析

【24择校指南】北方工业大学计算机考研考情分析

北方工业大学(B-) 考研难度&#xff08;☆☆&#xff09; 内容&#xff1a;23考情概况&#xff08;拟录取和复试分数人数统计&#xff09;、院校概况、23专业目录、23复试详情、23各科目和各专业考情分析。 正文1720字&#xff0c;预计阅读&#xff1a;5分钟。 2023考情概况…
阅读更多...
UGUI基础游戏对象Canvas

UGUI基础游戏对象Canvas

一.画布Canvas对象概述 画布是一种带有画布组件的游戏对象&#xff0c;所有 UI 元素都必须是此类画布的子项。 创建新的 UI 元素&#xff08;如使用菜单 GameObject > UI > Image 创建图像&#xff09;时&#xff0c;如果场景中还没有画布&#xff0c;则会自动创建画布。…
阅读更多...
在安装 ONLYOFFICE 协作空间社区版时如何使用额外脚本参数

在安装 ONLYOFFICE 协作空间社区版时如何使用额外脚本参数

ONLYOFFICE 协作空间社区版是免费的文档中心工具&#xff0c;可帮助您将用户与文档聚合至同一处&#xff0c;提高协作效率。 ONLYOFFICE 协作空间主要功能 使用 ONLYOFFICE 协作空间&#xff0c;您可以&#xff1a; 邀请他人&#xff0c;协作和沟通完成工作创建协作房间&…
阅读更多...
React(5)

React(5)

1.受控组件案例 1.1之前的影院案例改写 import React, { Component } from react import axios from axios import BetterScroll from better-scroll import ./css/02_tab.cssexport default class Cinema extends Component {constructor() {super();this.state {cinemaLis…
阅读更多...
谈谈闭包和闭包使用场景

谈谈闭包和闭包使用场景

一、什么是闭包 概念&#xff1a;闭包还是作用域的一种特殊应用 二、触发闭包的情况 1.函数当做返回值被返回 2.函数当做参数被传递 3.自执行匿名函数 //情况1&#xff1a;函数当做返回值被返回 function fn(){const a 1;return function(){console.log(a) //1}; } const a …
阅读更多...
每日一题——滑动窗口的最大值

每日一题——滑动窗口的最大值

滑动窗口的最大值 题目链接 暴力解法 最容易想到的当然还是通过两层循环来暴力求解&#xff1a;一层循环用来移动窗口&#xff0c;一层循环用来在窗口内找到最大值。这种做法的时间复杂度为O(kN)&#xff0c;会超出时间限制&#xff0c;因此&#xff0c;我们要找到更加高效的…
阅读更多...
【c语言】 -- 指针进阶

【c语言】 -- 指针进阶

&#x1f4d5;博主介绍&#xff1a;目前大一正在学习c语言&#xff0c;数据结构&#xff0c;计算机网络。 c语言学习&#xff0c;是为了更好的学习其他的编程语言&#xff0c;C语言是母体语言&#xff0c;是人机交互接近底层的桥梁。 本章来学习指针进阶。 让我们开启c语言学习…
阅读更多...
基于免费开源的Odoo平台搭建铸造行业的MES管理系统

基于免费开源的Odoo平台搭建铸造行业的MES管理系统

Odoo是世界排名第一的免费开源企业管理软件平台&#xff0c;该平台历经20年&#xff0c;构建了世界最大的企业软件应用市场&#xff0c;应用市场上有几万个插件&#xff0c;功能涵盖企业信息化的方方面面业务&#xff0c;包括CRM、ERP、MES、WMS、HRMS、OA、CMS等等。 今天介绍…
阅读更多...
新版PMP考试中，敏捷是怎么考的？

新版PMP考试中，敏捷是怎么考的？

01新版考试中的敏捷是怎么考的&#xff1f; 接下来说一下大家最为关注的敏捷内容。这次改版后&#xff0c;题目中添加了大量的敏捷题型&#xff0c;总体比重还是很高的&#xff0c;主观感觉达到了1/3。但和ACP认证相比&#xff0c;PMP中对敏捷管理技术的考察相对来说比较简单&…
阅读更多...
JDBC连接数据库如何实现你会吗？？？

JDBC连接数据库如何实现你会吗？？？

1.首先建立一个maven项目。。。详细过程来了哇 还没有安装maven的童鞋可以看这里&#xff1a;maven的下载安装与配置环境变量&#xff01;&#xff01;&#xff01;&#xff08;全网最详细&#xff09;_明天更新的博客-CSDN博客 有很多小伙伴就有疑问啦&#xff0c;难道我直接…
阅读更多...
云计算-知识点大纲

云计算-知识点大纲

前言&#xff1a;云计算的基本概念学习&#xff0c;基础知识大纲梳理。 目录 云计算的概念 云计算的特征 部署模式 服务模式 云计算的发展 云计算的核心技术 虚拟化技术 常见的虚拟化技术 服务器虚拟化 裸金属型技术 服务器虚拟化技术的特点 存储虚拟化 CPU 内存…
阅读更多...
iOS开发-WebRTC本地直播高分辨率不显示画面问题

iOS开发-WebRTC本地直播高分辨率不显示画面问题

iOS开发-WebRTC本地直播高分辨率不显示画面问题 在之前使用WebRTC结合ossrs进行推流时候&#xff0c;ossrs的播放端无法看到高分辨率画面问题。根据这个问题&#xff0c;找到了解决方案。 一、WebRTC是什么 WebRTC是什么呢&#xff1f; WebRTC (Web Real-Time Communicatio…
阅读更多...
Qt应用开发(基础篇)——拆分器窗口 QSplitter

Qt应用开发(基础篇)——拆分器窗口 QSplitter

一、前言 QSplitter继承于QFrame&#xff0c;QFrame继承于QWidget&#xff0c;是Qt的一个部件容器工具类。 框架类QFrame介绍 QSplitter拆分器&#xff0c;用户通过拖动子部件之间的边界来控制子部件的大小&#xff0c;在应用开发中数据分模块展示、图片展示等场景下使用。 二、…
阅读更多...
React集成tinymce插件

React集成tinymce插件

目录 一、Tinymce介绍 二、React集成Tinymce 1、安装tinymce/tinymce-react组件 2、React中引用 三、如何配置中文语言包 1、下载中文包 2、把语言文件放入tinymce 3、tinymce配置项中配置语言 一、Tinymce介绍 官网&#xff1a;The Most Advanced WYSIWYG Editor | T…
阅读更多...
Django路由Router

Django路由Router

文章目录 一、路由router路由匹配命名空间反向解析 二、实践创建用户模型Model添加子路由 - 创建用户首页页面跳转 - 使用反向解析和命名空间1. 不使用命名空间的效果2. 使用命名空间的效果 用户详情页面跳转 - 路由传参路由传递多个参数re_path 以前写法,了解即可重定向Redire…
阅读更多...
nodejs+vue+elementui美食网站的设计与实现演示录像2023_0fh04

nodejs+vue+elementui美食网站的设计与实现演示录像2023_0fh04

本次的毕业设计主要就是设计并开发一个美食网站软件。运用当前Google提供的nodejs 框架来实现对美食信息查询功能。当然使用的数据库是mysql。系统主要包括个人信息修改&#xff0c;对餐厅管理、用户管理、餐厅信息管理、菜系分类管理、美食信息管理、美食文化管理、系统管理、…
阅读更多...
【VB6|第23期】原来Jet.OLEDB也可以读取新版.xlsx的Excel文件

【VB6|第23期】原来Jet.OLEDB也可以读取新版.xlsx的Excel文件

日期&#xff1a;2023年8月11日 作者&#xff1a;Commas 签名&#xff1a;(ง •_•)ง 积跬步以致千里,积小流以成江海…… 注释&#xff1a;如果您觉得有所帮助&#xff0c;帮忙点个赞&#xff0c;也可以关注我&#xff0c;我们一起成长&#xff1b;如果有不对的地方&#xf…
阅读更多...
MySQL 小测试

MySQL 小测试

目录 基础查询 ​ 高级查询 基础查询 现有用户表user数据如下&#xff1a; 1、写出ddl语句创建如上表&#xff0c;插入数据&#xff0c;查询所有数据 #创建表user create table user( id int UNSIGNED auto_increment key , device_id int UNSIGNED, gender varchar…
阅读更多...
【算法】双指针——leetcode盛最多水的容器、剑指Offer57和为s的两个数字

【算法】双指针——leetcode盛最多水的容器、剑指Offer57和为s的两个数字

盛水最多的容器 &#xff08;1&#xff09;暴力解法 算法思路&#xff1a;我们枚举出所有的容器大小&#xff0c;取最大值即可。 容器容积的计算方式&#xff1a; 设两指针 i , j &#xff0c;分别指向水槽板的最左端以及最右端&#xff0c;此时容器的宽度为 j - i 。由于容器…
阅读更多...
七道Android面试题，先来简单热个身

七道Android面试题，先来简单热个身

作者&#xff1a;Coffeeee 马上就要到招(tiao)聘(cao)旺季金勾银十了&#xff0c;一批一批的社会精英在寻找自己的下一家的同时&#xff0c;也开始着手为面试做准备&#xff0c;回想起自己这些年&#xff0c;也大大小小经历过不少面试&#xff0c;有被面试过&#xff0c;也有当…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023