盛水最多的容器
(1)暴力解法
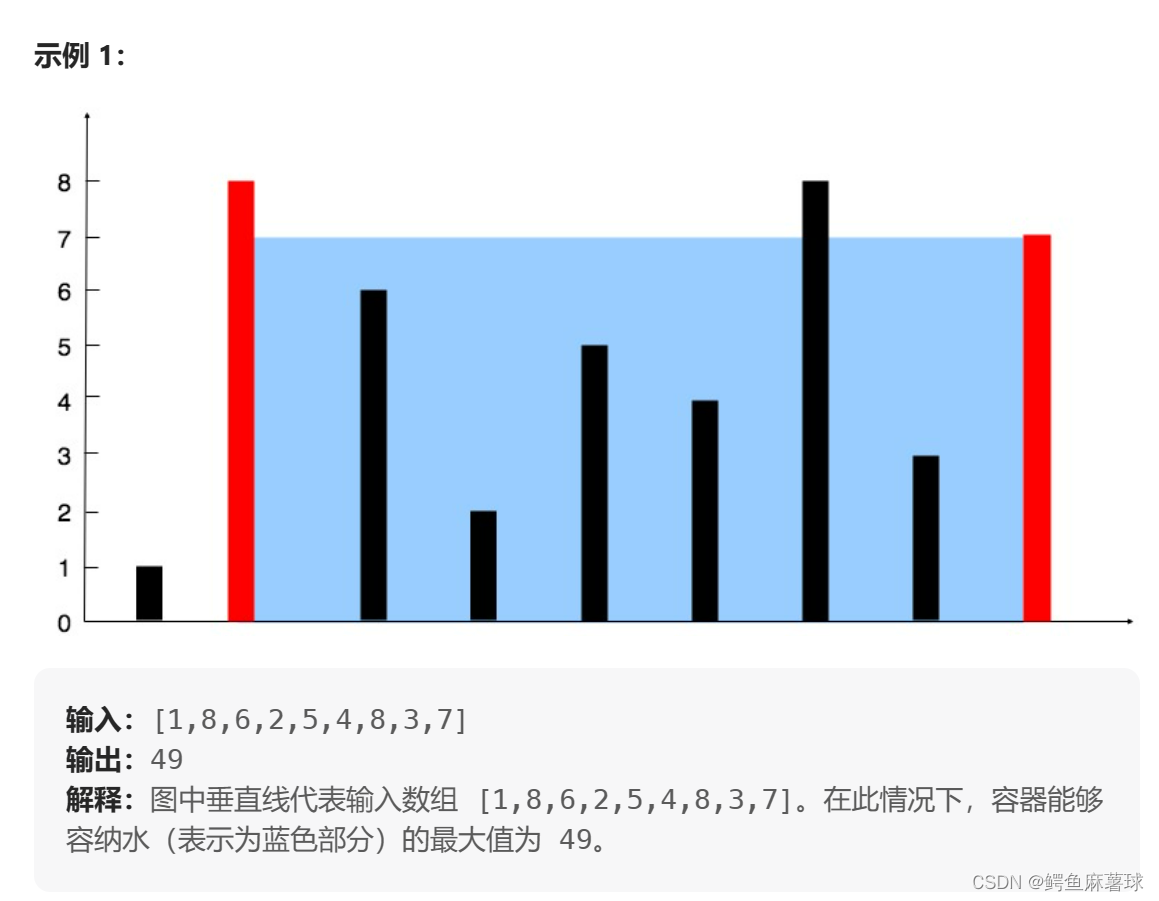
算法思路:我们枚举出所有的容器大小,取最大值即可。
容器容积的计算方式:
设两指针 i , j ,分别指向水槽板的最左端以及最右端,此时容器的宽度为 j - i 。由于容器的高度由两板中的较短的板决定,因此可得容积公式 :
v = (j - i) * min( height[i] , height[j] );
class Solution {
public:
int maxArea(vector<int>& height) {
int n=height.size();
int ret=0;
//枚举出所有的容器大小
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
//计算当前的容器容量
int v=(j-i)*(min(height[i],height[j]));
ret=max(ret,v);//取最大容量的容器
}
}
return ret;
}
};
当然由于两次遍历数组,所以时间复杂度为O(N2),会超时。
(2)对撞指针
算法思路:我们设置两个指针left、right分别指向容器的两个端点(因为这里的是数组,数组在内存中的储存是连续的,而且数组是通过它们的下表访问,所有我们可以把数组下标看成是指针进行操作)不断修改左右的端点来获得容器的最大容量。
容器的左边界为 height[left] ,右边界为 height[right] 。
我们假设「左边边界」小于「右边边界」。
水的容积会有如下变化形式:
首先容器的宽度⼀定变小。由于左边界较小,决定了水的高度。如果改变左边界,新的水面高度不确定,但是⼀定不会超过右边的柱子高度,因此容器的容积可能会增大或者减小。
但是如果改变右边界,无论右边界移动到哪⾥,新的水面的高度⼀定不会超过左边界,也就是现在左边界的所在的水面高度,但是由于容器的宽度减小,因此容器的容积一定会变小。
综上,我们不断选取左右两个边界中的较大边界,以保留当下的最有解,不断的 left++ 或right–,直到left和right相遇。
class Solution {
public:
int maxArea(vector<int>& height) {
int left=0;
int right=height.size()-1;
int ret=0;
//循环条件为右边界大于左边界
while(left<right)
{
//计算当前容器的容量
int v=(right-left)*(min(height[left],height[right]));
ret=max(v,ret);//不断更新容器的最大容量
if(height[left]>height[right]) right--;//不断更新左右高度
else left++; //保留高的,舍弃较矮的高
}
return ret;
}
};
时间复杂度:O(N)
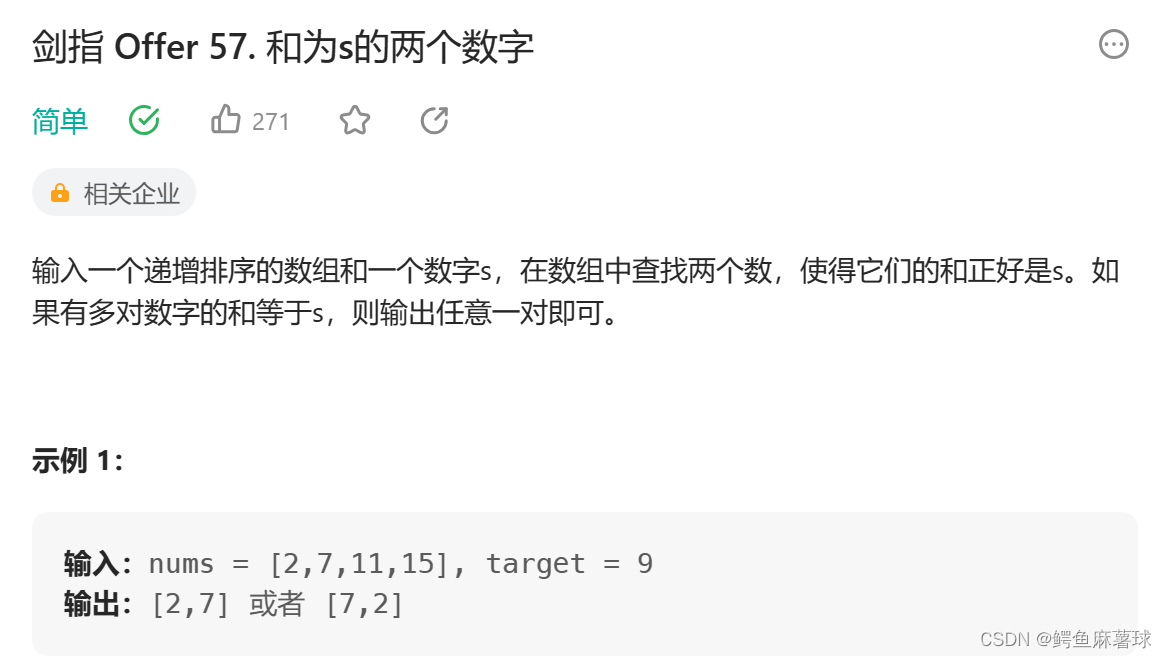
和为s的两个数字
和两数之和不同的是,该数组中的元素是有序的,而且使用暴力解法会超时。
(1)对撞指针
这里有三种情况:
当 nums[left] + nums[right] == target时,说明找到结果,记录结果,并且返回;
当 nums[left] + nums[right] < target 时,此时 nums[right] 相当于是 nums[left] 能碰到的最大值。如果此时不符合要求,说明我们需要增加这两个数之和,所以我们让left++,再取更大的数,以来靠近我们的目标和。
当 nums[left] + nums[right] > target 时,说明我们所取的两数较大,所以我们应该减小这两个数之和,让right–,以此使得两数的总和变小,以此来靠近我们的目标和。不断比较下⼀组数据,直至两数和和目标和相等。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int left=0;
int right=nums.size()-1;
while(left<right)
{
//如果两数和等于目标值,直接返回
if(nums[left]+nums[right]==target)
{
return {nums[left],nums[right]};
}//如果两数和大于目标值,right--
else if(nums[left]+nums[right]>target)
{
right--;
}//如果两数和小于目标值,left++
else
{
left++;
}
}
//照顾编译器,返回一个不存在的数组
return {-1141514};
}
};
时间复杂度:O(N)