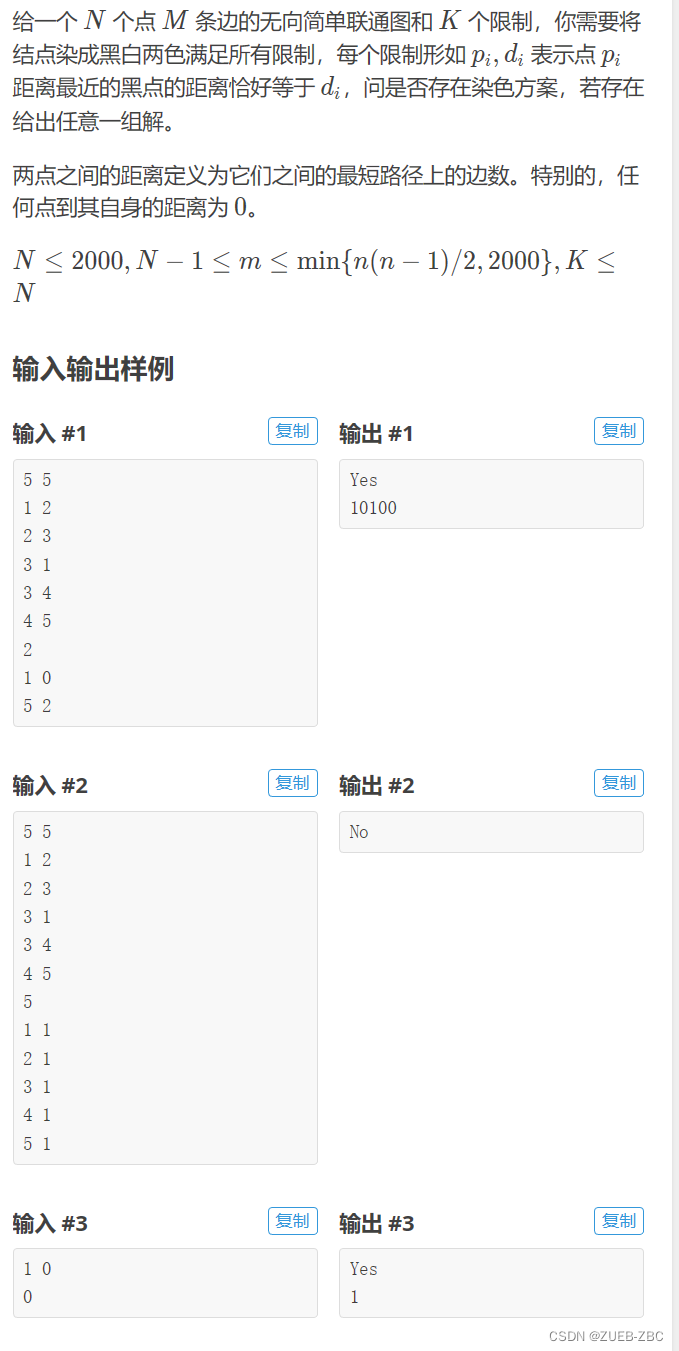
题目一

空间尝试模型 一个样本做行一个样本做列
范围尝试模型 以....做分隔
dp[i][j] 为以i为左界限 以j为右界限 求这个范围内的计算值(不对 是方法数)
这& | ^ 都是双目运算符 观察一下规律 整体字符数量一定为奇数(包括运算符和数字) 对应到数组中 数组的位一定是偶数 所以每个奇数行奇数列都不要 L不能超过R 下半区也不要(经典空间尝试模型)
那条件转移是什么呢 假设左界限 有界限 中间值为 x 那么i....x-1 x+1.....j 注意审题 是可以加括号也就是说可以决定运算顺序 也就是说 一个字符串的结果 不是固定的
条件转移是什么呢 假设左界限 有界限 中间有个位置为 x 那么i....x-1 x+1.....j
这个x位置肯定是个符号 自己举个例子就知道喵
当这个符号为&的时候 那简单 左边和右边都为1 结果才为1 左边右边有一个是0 都是0 总之就是左右相乘
但是|就比较麻烦 左1右0 为1 左0右1 为1 左1右1 为1 左0右0 为0
^呢 异或是 左1右1 为0 左0右1 左1右0 为1 左0右0 为0.
然后在这个基础呢 假如说 拿& 我左侧有3种方法为1 右侧有三种方法为1 那么我总的true的方法为 3*3对吧 记住这个dp[i][j]是方法数
所以要有两个dp数组 tdp 和 fdp 分别表示L到R范围内的(true/false)的方法数
basecase 是L==R的时候 如果是1 的话 那就是 tdp 当前位置有一种方法 0就是fdp位置有一种方法
否则为0
public static int ExpressionNumber0(String express, boolean desired){
char [] chars = express.toCharArray();
int N = chars.length;
int [][] tdp = new int [N][N];
int [][] fdp = new int [N][N];
for(int i = 0;i<N;i+=2) {
tdp[i][i] = chars[i] == '1'?1:0;//不用单引号就是ASCII码了
fdp[i][i] = chars[i] == '0'?1:0;
}
for (int row = N - 3; row >= 0; row -= 2) {
for (int col = row + 2; col < N; col += 2) {//行等于列的已经填完了 这次往上移动一下 就是两个格子 //col<的是N哦 所以是一行之内 先填前面 再填后面 所以可以依赖左方和下方
for (int i = row + 1; i < col; i += 2) {//用这个i枚举每一个分界点 顺便说下既然依赖于左下的格子
switch (chars[i]) {//注意这里行+1 是符号的位置 我得用它来确定转移方程 +1-1是格子的位置 格子的位置不能是符号位
case ('&')://记住是+= 这是累加的
tdp[row][col] += tdp[row][i-1]*tdp[i+1][col];
fdp[row][col] += fdp[row][i-1]*fdp[i+1][col]+fdp[row][i-1]*tdp[i+1][col]+tdp[row][i-1]*fdp[i+1][col];
break;
case('|'):
tdp[row][col] += tdp[row][i-1]*fdp[i+1][col] + fdp[row][i-1]*tdp[i+1][col]+tdp[row][i-1]*tdp[i+1][col];
fdp[row][col] += fdp[row][i-1]*fdp[i+1][col];
break;
case('^'):
tdp[row][col] += tdp[row][i - 1] * fdp[i + 1][col]+fdp[row][i - 1] * tdp[i + 1][col];
fdp[row][col] += tdp[row][i - 1] * tdp[i + 1][col]+fdp[row][i - 1] * fdp[i + 1][col];
break;
}
}
}
}
return desired?tdp[0][N-1]:fdp[0][N-1];
}题目二
给一个数组 划分多个数组 在哪一种划分下 能让异或和为0的更多
经典的从左往右尝试模型+范围尝试模型
dp[i] 表示从0...i最多有多少0
我们假设这种分法是 最多0的
(1) 当i位置(所属的块)异或和不为0的时候 dp[i] = dp[i-1]
(2) 当i位置(所属的块)异或和为0
假设答案法 假如说当前分法是最佳答案
假如其中有任意一块区域j...i那这之间肯定不存在一个k 让k...i异或和为0 因为你这相当于又切了 一块 我们开始已经假定这个是最优答案了 这就冲突了
那假设我们的最后一块区域为j....i 这个j 一定是 离i最近的 能让这块区域异或和为0的 0^0==0 所以
0....j j+1....i异或和都为0 我们找到j位置的答案 它再+1(我们现在说的这一块) 结果就是i位置的答案
public static int MostEOR(int [] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int [] dp = new int [arr.length];
dp[0] = arr[0]==0?1:0;
HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
int eor = 0;
map.put(0, -1);
map.put(arr[0],0);
for(int i = 1;i<arr.length;i++) {
eor^=arr[i];
if(map.containsKey(eor)) {
int pre = map.get(eor);
dp[i] = pre == -1 ? 1 : (dp[pre] + 1);//如果等于-1 就是异或和为0 直接算一种 当然如果后面又有0出现 那就回替换掉最开始的
//它只对应一种情况 从0...i累加和就是 0 且中间还没出现过其他的0 所以它只有一个0
}
dp[i] = Math.max(dp[i - 1], dp[i]);
map.put(eor, i);
}
return dp[dp.length - 1];
}和子序列一样 都是可能性的组织 几个可能性里面取一个most 既然要求最长/多 那就用most 是不是有点牵强了
我老觉得是 既然最后只有一种情况作为答案了 那为什么还要多个比较
答:有多种if 每种情况都可以选择 他们都是存在的 只是看我们的选择哪个作为这个位置的答案而已 所以选择多的那个
题目三
给出一组正整数arr,你从第0个数向最后一个数,
每个数的值表示你从这个位置可以向右跳跃的最大长度
计算如何以最少的跳跃次数跳到最后一个数。
首先我们要理解 不是每个点都跳到最远好 因为你可能会错过一个大长度
而且这个模型不用考虑往回跳 因为你完全可以中间停下来 为啥要往回跳
五步最远能跳多远
四步最远的地方 一定比五步最远跳的近(废话)
四步每个能到的位置 加上自身的值 其中一定有一个是五步的右边界(走到最远的地方)
第一步我可以走到 i的位置 也就是说第一步的区间是0...i 这个区间里我可以选择任何一个地方作为落脚点 走第二步 但是目前我们看不出 我们可以选择在哪落脚是迈出第二步是最优解 不过没关系 我们直接枚举每一个落脚点 看看最远能走到哪 也就是找出第三步的区间...以此类推 看看最先什么时候扩到对应区间
感觉有哪不通?我也是
对于第四步来说 假如我选了其中一个落脚点 那么我这个落脚点走不到5步的区间的最右怎么办?那就不要选啊 就选能到达最边界的步 那我到达了最边界 最边界上面的步数 是一个很小的点那下一步怎么扩充 无所谓啊 我们会枚举每一个落脚点 来扩充下一步 对于每一个区间 它的每一点都是可达的 然后用它扩充出来的区间 也一样是可达的 所以不同区间所有点都是可达的 如果这个点肯定是上一个区间的某个点跳过来的 那这个调过来的点 也是上上个区间调过来的
public static int jump(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int step = 0; // 跳了多少步
int cur = 0; // step步内,右边界
int next = 0;// step+1步内,右边界
for (int i = 0; i < arr.length; i++) {
if (cur < i) {
step++;
cur = next;
}
next = Math.max(next, i + arr[i]);
}
return step;
}被笔记骗了 压根没有什么flag -1



![C#,入门教程(42)——各种括号“()[]{}<>“的用法总结](https://img-blog.csdnimg.cn/img_convert/27451320ed3c4a27b5a207a53ebd3ec9.png)