第 301 场周赛
C:
思路:
经典双指针问题,用i表示字符串start当前枚举到的位置,用j表示字符串target当前枚举到的位置:
-
i从当前位置向后跑,跑到start串下标i之后的第一个不为'_'的位置
-
j从当前位置向后跑,跑到target串下标j之后的第一个不为'_'的位置
-
判断start[i]与target[j]是否相同,如果不同,指定是无解了。
-
如果当前start[i]=='L'时,应该是i>=j,如果是'R'则应该是i<=j,否则无解。
-
检查i<n and j<n,如果满足,返回步骤1,重复执行操作,否则进行步骤6
-
如果i<n-1,检查start,同理检查target字符串,之后的字符应全是'_'
代码:
class Solution: def canChange(self, start: str, target: str) -> bool: n=len(start) i=j=0 while i<n and j<n: while i<n and start[i]=='_': i+=1 while j<n and target[j]=='_': j+=1 if i<n and j<n: if start[i]!=target[j]: return False c=start[i] if c=='L' and i<j or c=='R' and i>j: return False i+=1 j+=1 while i<n: if start[i]!='_': return False i+=1 while j<n: if target[j]!='_': return False j+=1 return True
D: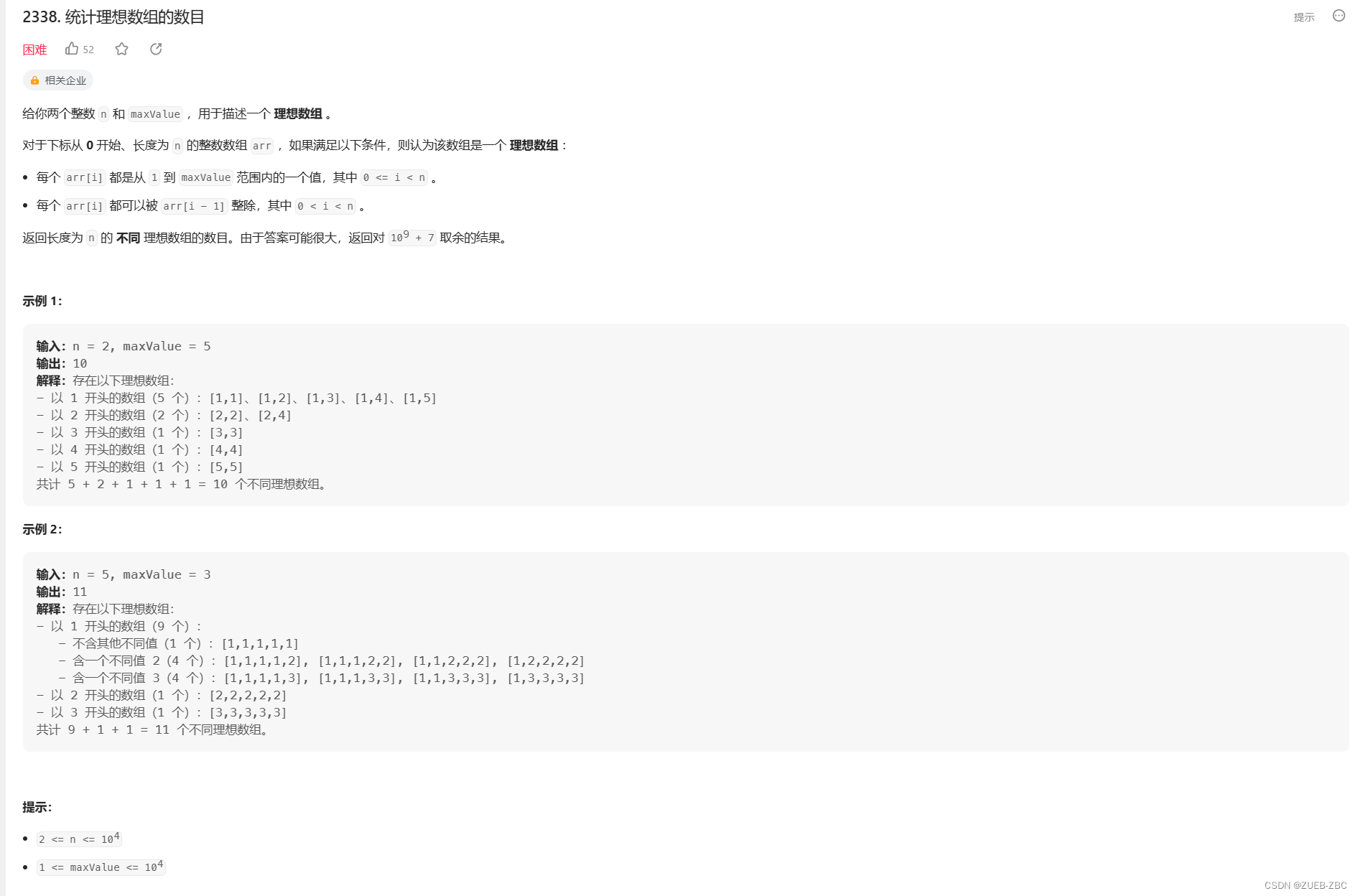
思路:
不会,参考题解
数学 & 递推,附复杂度与 n 无关(klogk)的做法:
2338. 统计理想数组的数目 - 力扣(LeetCode)
代码
class Solution {
const int MOD=1e9+7;
const int MAXP=16;
public:
int idealArrays(int n, int K) {
//nlnn求因数
vector<vector<int>>fac(K+1);
for(int i=1;i<=K;i++){
for(int j=i<<1;j<=K;j+=i){
fac[j].push_back(i);
}
}
//计算子问题答案,f[i][j]表示以i为结束元素,长度为j的方案个数,长度为j的序列元素两两不同
vector<vector<long long>>f;
f.resize(K+1,vector<long long>(20));
for(int i=1;i<=K;i++){
f[i][1]=1;
for(int j=2;j<=MAXP;j++){
for(int t:fac[i]){
f[i][j]=(f[i][j]+f[t][j-1])%MOD;
}
}
}
//求组合数
vector<vector<long long>>C;
C.resize(n+1,vector<long long>(20));
C[0][0]=C[1][0]=C[1][1]=1;
for(int i=2;i<=n;i++){
C[i][0]=1;
for(int j=1;j<=i&&j<=MAXP;j++){
C[i][j]=(C[i-1][j]+C[i-1][j-1])%MOD;
}
}
//统计最终答案
long long ans=0;
for(int i=1;i<=K;i++){//终点
for(int j=1;j<=MAXP;j++){//选几个数
ans=(ans+C[n-1][j-1]*f[i][j])%MOD;
//最终元素为i,从n个元素里面选取长度为j的不重复元素,将这j个不重复元素确定好位置,这个长度为n
//的序列就确定了,那么第一个最小的元素肯定在位置1,那剩下来的n-1个位置,放置j-1个数就行了
//因为最终元素为i,长度为j的序列中元素两两不同的方案书为f[i][j],选取的位置有C[n-1][j-1]
//所以乘法原理即可
}
}
return ans;
}
};ABC299
D - Find by Query
题目大意:
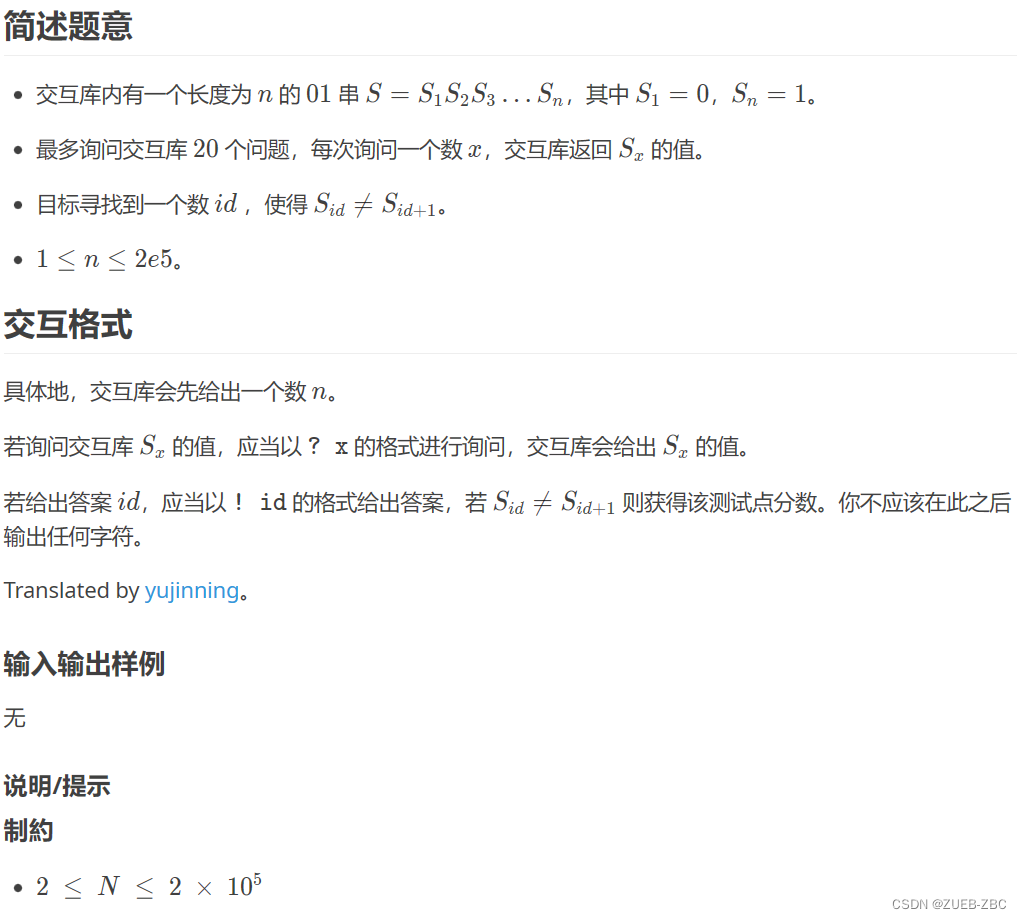

思路:
看到最多询问20次,长度为2e5,首先想到的应该是二分,怎么二分呢?
注意到S[1]='0',S[N]='1',那么每次查询中间的位置,如果query(l+r>>1)=='0',那就令l=l+r>>1,否则r=l+r>>1
,这样就能时刻保证S[l]='0',S[r]='1'
代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
int l = 1, r = n;
int cnt = 20;
while (cnt > 0)
{
cnt--;
int mid = l + r >> 1;
cout << "? " << mid << endl;
char x;
cin >> x;
if (l + 1 == mid && x == '1')
{
cout << "! " << l << endl;
return 0;
}
if (mid + 1 == r && x == '0')
{
cout << "! " << mid << endl;
return 0;
}
if (x == '0')
{
l = mid;
}
else
{
r = mid;
}
}
return 0;
}E - Nearest Black Vertex
题目大意:
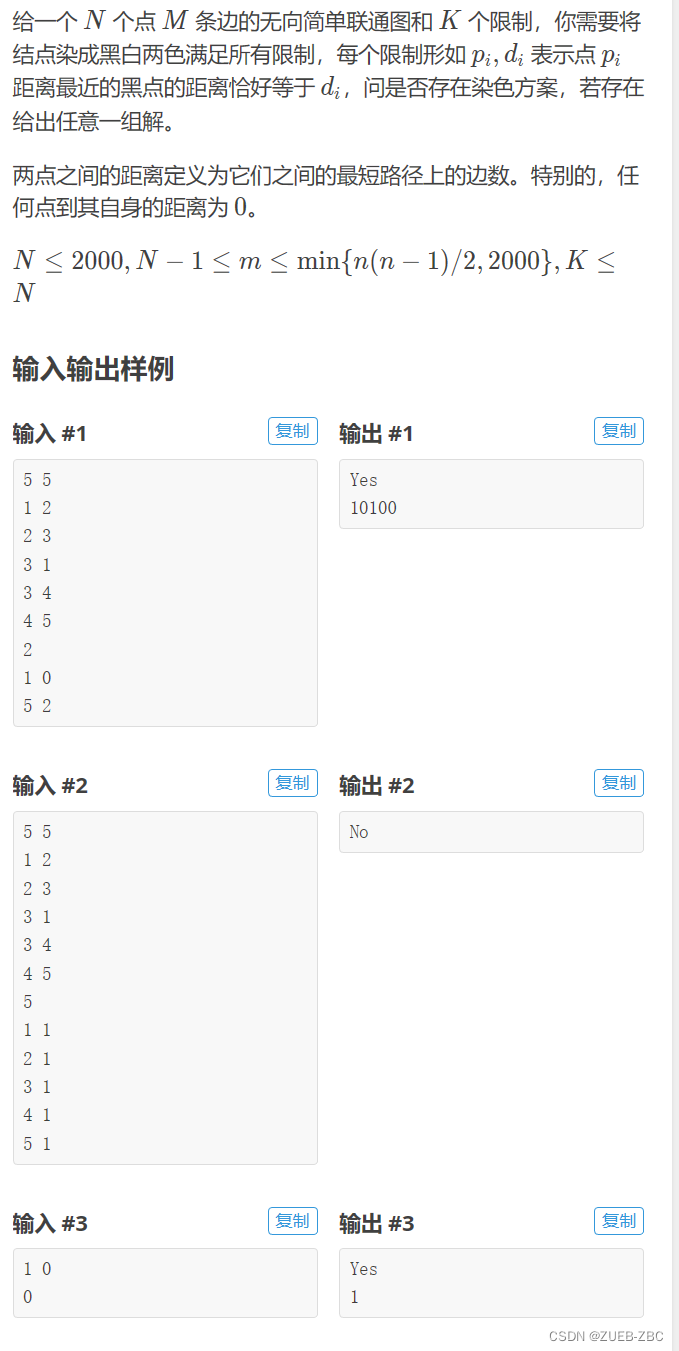
思路:
-
首先建图,然后跑最短路,堆优化迪杰斯特拉的时间复杂度为O(M*log(N)),但是这个题边权全为1,就不需要堆优化了,普通队列即可,所以求以每一个点s(1<=s<=n)为起点到其他点的最短路径的时间复杂度为O(NM)
-
读入k个限制,u,d,遍历以u为起点,到其他点(下面用v表示)的最短路径,如果
dist[ u ][ v ] < d
,则这个点不可能是黑色点,标记
-
全部标记完之后,再次遍历k个限制,遍历每个限制是否有解即可
即寻找dist[u][v]==d,是否有点满足,并且这个点v没有被标记为不能做为黑色点
代码:代码写的与思路有一点不一样,我的代码在读入限制的时候就判断他有没有可行点解了,就是
dist[u][v]==d是否存在,如果已经找到一个点不满足就不接着做了,直接输出No即可,现在看来有点鸡肋了,即使这样做,等k个限制跑完之后,仍然需要再次跑k个限制看看是否满足条件,因为假如你 u1,找到某个唯一可以当作黑色点的v1,此时这个v1还没有被标记为不能当作黑点 接下来限制u2 d的时候,把v1标记做了不能当作黑点,只遍历一遍是不行的也就是说如果说只有这两个限制,只跑一边会输出Yes,然后输出可行解,但实际是No,因为u1的唯一可以当作黑点的v1被u2 hcak掉了
#include <bits/stdc++.h>
using namespace std;
#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define PII pair<int, int>
#define de(a) cout << #a << " = " << a << "\n";
#define deg(a) cout << #a << " = " << a << " ";
#define endl "\n"
#define int long long
#define LL long long
const int mod = 1e9 + 7;
const int N = 1e6 + 5;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
vector<int> edge[N];
int dist[2005][2005];
int n, m;
void dijkstra(int s)
{
vector<int> vis(n + 1, 0);
dist[s][s] = 0;
queue<int> q;
q.push(s);
while (q.size())
{
int t = q.front();
q.pop();
if (vis[t])
continue;
vis[t] = true;
for (auto v : edge[t])
{
if (dist[s][v] > dist[s][t] + 1)
{
dist[s][v] = dist[s][t] + 1;
q.push(v);
}
}
}
}
void solve()
{
cin >> n >> m;
for (int i = 0; i <= n + 1; i++)
{
for (int j = 0; j <= n + 1; j++)
{
dist[i][j] = INT64_MAX;
}
}
for (int i = 0; i < m; i++)
{
int u, v;
cin >> u >> v;
edge[u].push_back(v);
edge[v].push_back(u);
}
for (int i = 1; i <= n; i++)
{
dijkstra(i);
}
int k;
vector<int> st(n + 1, 1);
cin >> k;
vector<PII> query;
bool ok = true;
for (int i = 0; i < k; i++)
{
int u, d;
cin >> u >> d;
query.emplace_back(u, d);
bool f = 0;
for (int v = 1; v <= n; v++)
{
if (dist[u][v] < d)
{
st[v] = 0; // 不能为黑色
}
else if (dist[u][v] == d && st[v] == 1) // 找到合法黑色点了
{
f = 1;
}
}
if (!f) // 这个点u没有合法点当u
ok = 0;
}
for (int i = 0; i < k; i++)
{
auto [u, d] = query.back();
query.pop_back();
bool f = 0;
for (int v = 1; v <= n; v++)
{
if (dist[u][v] < d)
{
st[v] = 0; // 不能为黑色
}
else if (dist[u][v] == d && st[v] == 1) // 找到合法黑色点了
{
f = 1;
}
}
if (!f) // 这个点u没有合法点当u
ok = 0;
}
if (ok)
{
cout << "Yes\n";
for (int i = 1; i <= n; i++)
{
cout << st[i];
}
}
else
{
cout << "No\n";
}
}
signed main()
{
FAST;
int t = 1;
// cin >> t;
while (t--)
solve();
return 0;
}G - Minimum Permutation
题目:
有一个长度为 N 的序列,保证其中包含1~M,请你找到一个长M的子序列,使得其中每个数字都出现了一次,并使得排列的字典序最小。
思路:
贪心。考虑单调栈(定义s[i]表示栈中第i个元素是什么,tt表示现在的栈顶元素所在的位置),顺序枚举这个长度为N的序列。
假如我们现在处理第i个元素,那么前i-1个元素已经处理好了,对于第i个元素a[i],
-
如果a[i]在栈里,直接跳过就行了
-
a[i]>s[tt](栈顶),直接加到栈里面就可以了
-
a[i]<s[tt](栈顶),判断当前栈顶所在元素在 [i +1~n]在后面是否出现过,如果出现过,可以放心的把栈顶去掉了,循环次操作,然后将a[i]加入栈顶就可以了。这样一定是正确的,因为我们去掉栈顶的条件是栈顶小于当前元素(保证字典序更小),后面出现过当前栈顶(保证后面可以把这个删去的栈顶加进来)
#include <bits/stdc++.h> using namespace std; #define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0) #define PII pair<int, int> #define de(a) cout << #a << " = " << a << "\n"; #define deg(a) cout << #a << " = " << a << " "; #define endl "\n" #define int long long #define LL long long const int mod = 1e9 + 7; const int N = 1e6 + 5; int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1}; int n, m, a[N], s[N], tt, d[N]; bool st[N]; void solve() { int n, m; cin >> n >> m; for (int i = 1; i <= n; i++) { cin >> a[i]; d[a[i]]++; } for (int i = 1; i <= n; i++) { d[a[i]]--; // 这个数字出现过了一次 if (st[a[i]]) continue; while (s[tt] > a[i] && d[s[tt]]) // 栈顶大于当前元素,并且栈顶的元素在后面还有 st[s[tt]] = 0, tt--; s[++tt] = a[i]; st[a[i]] = 1; } for (int i = 1; i <= m; i++) { cout << s[i] << ' '; } } signed main() { FAST; int t = 1; // cin >> t; while (t--) solve(); return 0; }