1. 题目链接：46. 全排列

2. 题目描述：给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

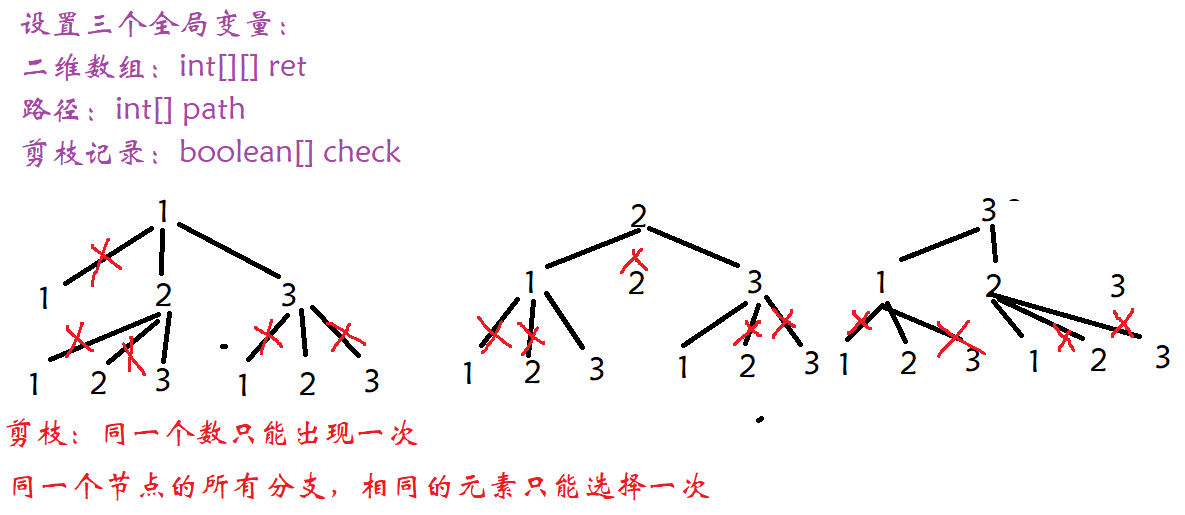
递归流程如下：
1. 首先定义一个二维数组 res 用来存放所有可能的排列，一个一维数组 ans 用来存放每个状态的排列，一个一维数组 visited 标记元素，然后从第一个位置开始进行递归；
2. 在每个递归的状态中，我们维护一个步数 step，表示当前已经处理了几个数字；
3. 递归结束条件：当 step 等于 nums 数组的长度时，说明我们已经处理完了所有数字，将当前数组存入结果中；
4. 在每个递归状态中，枚举所有下标 i，若这个下标未被标记，则使用 nums 数组中当前下标的元
素：
a. 将 visited[i] 标记为 1；
b. ans 数组中第 step 个元素被 nums[i] 覆盖；
c. 对第 step+1 个位置进行递归；
d. 将 visited[i] 重新赋值为 0，表示回溯；
5. 最后，返回 res。
• 特别地，我们可以不使用标记数组，直接遍历 step 之后的元素（未被使用），然后将其与需要递
归的位置进行交换即可。 

class Solution {
    List<List<Integer>> ret;
    List<Integer> path;
    boolean[] check;
    public List<List<Integer>> permute(int[] nums) {
        int n=nums.length;
        ret=new ArrayList<>();
        path=new ArrayList<>();
        check=new boolean[n];
        
        dfs(nums);
        return ret;
    }
    public void dfs(int[] nums){
        if(nums.length==path.size()){
            ret.add(new ArrayList<>(path));
            return ;
        }
        for(int i=0;i<nums.length;i++){
            if(check[i]==false){
                path.add(nums[i]);
                check[i]=true;
                dfs(nums);
                check[i]=false;
                path.remove(path.size()-1);
            }
        }
    }
}