10-数据结构-队列（C语言）

news2024/11/24 2:00:52

队列

目录

目录

队列

一、队列基础知识

二、队列的基本操作

1.顺序存储

​编辑 （1）顺序存储

（2）初始化及队空队满

（3）入队

（4）出队

（5）打印队列

（6）循环队列

（7）顺序可运行总代码：

2.链式存储

(1)链式存储定义

(2)初始化

(3)进队

(4)出队

(5)打印链队

(6)链队可运行总代码

3.双端队列。

(1)输入受限的双端队列

(2)输出受限的双端队列

(3)例题：

一、队列基础知识

        简介：队列是一种先进先出（FIFO）的线性数据结构，是一种只允许在一端进行插入操作（队尾），在另一端进行删除操作的数据结构（队头）。插入操作在队列的末尾进行，删除操作在队列的前端进行，即队头元素先出队，后插入的元素排在队尾。

        队列是一种广泛应用于计算机科学领域的数据结构，常用于实现消息队列、任务队列、缓冲队列等。在算法设计中，队列可以用于广度优先搜索（BFS）、模拟银行排队等问题。同时，队列还常与栈结构搭配使用，实现更复杂的算法和数据结构。

二、队列的基本操作

        简介：队列可以使用数组或链表实现。常见的队列操作包括：入队（enqueue）、出队（dequeue）、获取队头元素（front）、获取队列长度（size）等。

1.顺序存储

        简介：就是数组+两个标记队头和队尾的变量，构成的结构体。

        优点：简单易实现。

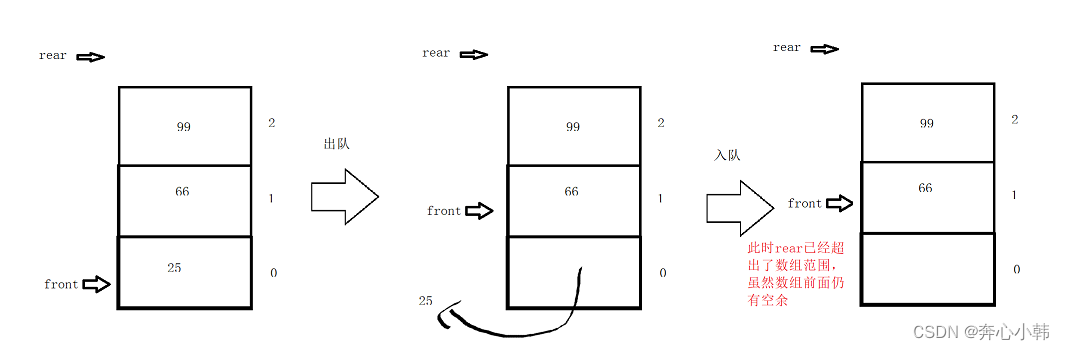
        缺点：容易出现假溢出问题（队列未满时，向队列尾插入元素却因为队列头指针没有移动而导致队列满的情况）。

 （1）顺序存储

        即一个一维数组和两个标记队头和队尾的变量。

代码如下：

//队列的顺序存储
#define MaxSize 10
typedef struct
{
	int data[MaxSize];
	int front;
	int rear;
  //  int count;//记录队列中实际元素个数,可先不用
}SqQueue;

（2）初始化及队空队满

        初始化：

//队列初始化
void QueueInit(SqQueue *q)
{
	q->front=0;	
	q->rear=0;
}

        队空：当队头和队尾相等的时候便为空。不仅仅限制于都等0，因为两个变量都在一直变化。

//队空
bool QueueEmpty(SqQueue *q) 
{
	if(q->front == q->rear )
	return true;
}

        队满：这里面队满不好判定，当rear>MaxSize-1时，会出现假溢出现象，不算队满。不过可以在队列顺序存储时结构体里面加一个计时器，出队一次，count--，入队一次count++，当count==MaxSize-1时，队满。

typedef struct
{
	int data[MaxSize];
	int front;
	int rear;
	int count;
}SqQueue; 
//队满
bool QueueFull(SqQueue *q)
{
	if(q->count == MaxSize-1)
	return true;
}

（3）入队

        从队尾rear处进行遍历，入队赋值。随后rear+1，后撤。

//入队
void EnQueue(SqQueue *q,int x)
{
	//如果队满了 
	if(QueueFull(q)==false)
		exit(-1);
	//给队尾处赋值 
	q->data[q->rear]=x;
	//移动队尾标记 
	q->rear++;
	//数据数+1； 
	q->count++;
}

（4）出队

//出队
void OutQueue(SqQueue *q,int *e)
{
	//判断非法情况，是否为空 
	if(q->front == q->rear)
		exit(-1);
	//取出队头元素，赋值给e 
	*e=q->data[q->front];
	//队头指针++ 
	q->front++;
	//元素个数-1； 
	q->count--;
}

（5）打印队列

void QueuePrint(SqQueue *q)
{
	int i=0;
	printf("目前队列中有%d个数据\n",q->count);
	//从队头遍历到队尾 
	for(i=q->front;i<q->rear;i++)
	{
		printf("%d ",q->data[i]);	
	}
	printf("\n");	
}

（6）循环队列

        简介：由于普通的顺序存储队列，存在假溢出现象，导致出队后，出现的空缺，没法补上，这时候循环队列就出手了。它则是多了个取余操作，每次模数组最大值，给溢出的数字，控制在最大值之内，达到循环，形成了一个环。

        即每一次标记队头和队尾遍历，变换时，变为了q->front=(q->front+1)%MaxSize;q->rear=(q->rear+1)%MaxSize;

        此外，循环队列，在判断队满时，一般两种操作：

        一个是牺牲最后一个格子，当rear+1=front时，此时队满。

        另一个操作则是：像我最开头，在结构体定义里面加一个记录实际数据的计数器，每次出队入队，计数器进行相应的加减。当计数器等于MaxSize时，队满。

        此外，循环队列的长度计算为：[MaxSize-(q->rear  -  q->front)]%MaxSize;但如果，之前在结构体里面加了一个计数器，则直接打印计数器即可。

        下面时循环队列的操作。

        入队：（只不过比之前入队，多了一个判断队满的判断，以及移动队尾指针时取余）

void CycEnQueue(SqQueue *q,int x)
{
	//如果队满了 
	if(QueueFull(q)==1) //可以在结构体中加个计数器
		exit(-1);
    //if(q->rear+1 == q->front)  //也可以牺牲一个存储单元，用来判断队满
	//	exit(-1);
	//给队尾处赋值 
	q->data[q->rear]=x;
	//移动队尾标记 
	q->rear=(q->rear+1)%MaxSize;
	//数据数+1； 
	q->count++;
}

        出队：   

void CycOutQueue(SqQueue *q,int *e)
{
	//判断非法情况，是否为空 
	if(q->front == q->rear)
		exit(-1);
	//取出队头元素，赋值给e 
	*e=q->data[q->front];
	//队头指针++ 
	q->front=(q->front+1)%MaxSize;
	//元素个数-1； 
	q->count--;
}

（7）顺序可运行总代码：

#include <stdio.h>
#include <stdlib.h> 
//队列 
//队列的顺序存储
#define MaxSize 10
typedef struct
{
	int data[MaxSize];
	int front;
	int rear;
	//计数器 
	int count;
}SqQueue; 
//队列初始化
void QueueInit(SqQueue *q)
{
	q->front=0;	
	q->rear=0;
	q->count=0;
} 
//队空
int QueueEmpty(SqQueue *q) 
{
	if(q->front == q->rear )
	return 1;
}
//队满
int QueueFull(SqQueue *q)
{
	if(q->count == MaxSize-1)
	return 1;
	else
	return -1;
}
//入队
void EnQueue(SqQueue *q,int x)
{
	//如果队满了 
	if(QueueFull(q)==1)
		exit(-1);
	//给队尾处赋值 
	q->data[q->rear]=x;
	//移动队尾标记 
	q->rear++;
	//数据数+1； 
	q->count++;
} 
void CycEnQueue(SqQueue *q,int x)
{
	//如果队满了 
	if(q->rear+1 == q->front)
		exit(-1);
	//给队尾处赋值 
	q->data[q->rear]=x;
	//移动队尾标记 
	q->rear=(q->rear+1)%MaxSize;
	//数据数+1； 
	q->count++;
} 
//出队
void OutQueue(SqQueue *q,int *e)
{
	//判断非法情况，是否为空 
	if(q->front == q->rear)
		exit(-1);
	//取出队头元素，赋值给e 
	*e=q->data[q->front];
	//队头指针++ 
	q->front++;
	//元素个数-1； 
	q->count--;
} 
void CycOutQueue(SqQueue *q,int *e)
{
	//判断非法情况，是否为空 
	if(q->front == q->rear)
		exit(-1);
	//取出队头元素，赋值给e 
	*e=q->data[q->front];
	//队头指针++ 
	q->front=(q->front+1)%MaxSize;
	//元素个数-1； 
	q->count--;
} 
//打印队列
void QueuePrint(SqQueue *q)
{
	int i=0;
	printf("目前队列中有%d个数据\n",q->count);
	//从队头遍历到队尾 
	for(i=q->front;i<q->rear;i++)
	{
		printf("%d ",q->data[i]);	
	}
	printf("\n");	
} 


//队列的链式存储 

int main()
{
	//创建队列 
	SqQueue q;
	//初始化队列 
	QueueInit(&q);
	//打印队列 
	QueuePrint(&q);
	//入队 
	EnQueue(&q,0); 
	EnQueue(&q,1); 
	EnQueue(&q,2); 
	EnQueue(&q,3); 
	QueuePrint(&q);
	//出队 
	int e=0;
	OutQueue(&q,&e);
	QueuePrint(&q);
	printf("出队%d\n",e);
	return 0;
}

2.链式存储

        简介：使用链表数据结构实现，每个节点都包含一个元素和指向下一个节点的指针。

        链表队列的优点：可以动态地调整队列长度。

        链表队列的缺点：需要更多的内存空间存储指针信息。另外，由于需要动态申请和释放内存，链表实现的队列在操作上比数组实现的队列稍慢

(1)链式存储定义

        简介：由单链表构成，然后由队头指针和队尾指针，进行操作，因此定义两个结构体，一个结构体是定义队列结点类型的，一个则是封装队头，队尾指针。

/链队结点
typedef struct Linknode
{
	int data;
	struct Linknode* next; 
}LinkNode;
//链队的头指针和尾指针 
typedef struct
{
	LinkNode* front;
	LinkNode* rear;
}LinkQueue;

(2)初始化

这里面初始化，默认带头节点，就是为了是开头操作和其他情况操作一致。

/链队初始化
void InitQueue(LinkQueue* q)
{
	//创建头节点
	LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
	if (s == NULL)
		exit(-1);
	else
	{
		s->next = NULL;
		q->front = q->rear = s;
		q->rear->next = NULL;
	}
	//return q;
}

初始化的时候，头节点定义完后，队头指针和队尾指针都指向它，并且队尾指针的指针域指向空。

(3)进队

进队时，也是先定义一个队列结点，用来加入队。随后用队尾指针进行相关操作。先连接结点，再更新队尾指针。

//入队
void   EnQueue(LinkQueue* q, int x)
{
	//创建结点
	LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
	if (s == NULL)
		exit(-1);
	else
	{
		s->data = x;
		s->next = NULL;
		//队尾所指向的结点的指针域，指向存储s结点地址
		q->rear->next = s;
		//更新尾指针
		q->rear = s;
	}
	
}

(4)出队

出队时，先判断是否为空队，随后，再进行出队操作，出队时，先定义一个指针，指向需要出队的元素，因为这里由头节点，而队头指针始终指向头节点，因此标记出队元素指针为队头指针的指针域，即头节点的后继节点为实际出队结点。随后头节点的指针域，指向出队结点的后继，并判断，当前出队的元素是否为最后一个结点，即如果q->rear = p，则让队内初始化为空，即队头指针和队尾指针相等。随后释放掉P结点。

//出队
void  DeQueue(LinkQueue* q, int* e)
{
	//判断非法情况，空队 
	if (q->front == q->rear)
		exit(-1);
	//给出队元素赋值 
	*e = q->front->next->data;
	//标记出队元素 
	LinkNode* p = q->front->next;
	//队头指针后移到出队元素后继节点 
	q->front->next = p->next;
	//判断是否仅有一个结点 
	if (q->rear == p)
	{
		q->rear = q->front;
	}
	free(p);
	//return q;
}

(5)打印链队

定义一个工作指针，

工作指针，从实际第一个元素结点开始，即头节点的后继节点。

void LinkQueuePrint(LinkQueue* q)
{
	LinkNode* pos = q->front->next;//队头元素指向头节点
	int i = 0;
	while (pos !=NULL)
	{
		printf("%d->", pos->data);
		pos = pos->next;
	}

	printf("NULL\n");
}

(6)链队可运行总代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h> 
//链队结点
typedef struct Linknode
{
	int data;
	struct Linknode* next; 
}LinkNode;
//链队的头指针和尾指针 
typedef struct
{
	LinkNode* front;
	LinkNode* rear;
}LinkQueue;
//链队初始化
void InitQueue(LinkQueue* q)
{
	//创建头节点
	LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
	if (s == NULL)
		exit(-1);
	else
	{
		s->next = NULL;
		q->front = q->rear = s;
		q->rear->next = NULL;
	}
	//return q;
}
//入队
void   EnQueue(LinkQueue* q, int x)
{
	//创建结点
	LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
	if (s == NULL)
		exit(-1);
	else
	{
		s->data = x;
		s->next = NULL;
		//队尾所指向的结点的指针域，指向存储s结点地址
		q->rear->next = s;
		//更新尾指针
		q->rear = s;
	}
	
	//return q;
}
//出队
void  DeQueue(LinkQueue* q, int* e)
{
	//判断非法情况，空队 
	if (q->front == q->rear)
		exit(-1);
	//给出队元素赋值 
	*e = q->front->next->data;
	//标记出队元素 
	LinkNode* p = q->front->next;
	//队头指针后移到出队元素后继节点 
	q->front->next = p->next;
	//判断是否仅有一个结点 
	if (q->rear == p)
	{
		q->rear = q->front;
	}
	free(p);
	//return q;
}
void LinkQueuePrint(LinkQueue* q)
{
	LinkNode* pos = q->front->next;//队头元素指向头节点
	int i = 0;
	while (pos !=NULL)
	{
		printf("%d->", pos->data);
		pos = pos->next;
	}

	printf("NULL\n");
}
int main()
{
	 LinkQueue q ;
	 InitQueue(&q);
	 EnQueue(&q, 0);
	 EnQueue(&q, 1);
	 EnQueue(&q, 2);
	 EnQueue(&q, 3);
	LinkQueuePrint(&q);
	int e = 0;
	DeQueue(&q, &e);
	printf("e=%d\n", e);
	LinkQueuePrint(&q);
	DeQueue(&q, &e);
	printf("e=%d\n", e);
	LinkQueuePrint(&q);
	return 0;
}

3.双端队列。

这一部分了解思想即可，主要用于计算选择和填空。

        简介：

        双端队列（Double-ended Queue）是一种特殊的队列，它允许在队列两端进行插入和删除操作。双端队列可以看作是两个栈首尾相接构成的数据结构。在双端队列中，可以在队列头部和尾部进行元素的插入和删除操作，因此它的操作有：从队头插入元素、从队头删除元素、从队尾插入元素、从队尾删除元素等。

双端队列可以用数组或链表实现。在数组中实现时，需要注意队列头部和尾部指针的位置。当队列长度大于数组长度时，需要进行扩容操作。在链表中实现时，只需要维护头结点和尾结点即可。

双端队列的应用非常广泛，比如操作系统中的进程调度队列、窗口滑动中的数据缓存等场景都可以使用双端队列来实现。        

说白了，就是再原来队列的基础上，多了好几个功能，即两端都可以进行入队和出队操作。

        之后，便引申出了一个题型。输入受限的双端队列，输出受限的双端队列。

(1)输入受限的双端队列

        即一段仅能输出，另一端输入输出都可以，就是仅能输出那一段，不能输入，就是输入受限。

        这里记住一个技巧：若1234为入队序列，那么输入受限的话，有这样公式：..1..2..3..4,即先先出4的话，2就不能紧跟着出。因为2位于1 3中间。这种技巧是可以得到不可能得到的序列

(2)输出受限的双端队列

        即一段仅能输入，另一端不限制，就是仅能输入那一段，不能输出，就是输出受限。

        技巧：若1234入队序列，那么有这样公式：12...3..4,这时4输出了，那么3一定不会12之间，因为12是紧挨着的。这种技巧是可以得到不可能得到的序列

(3)例题：

        有一双端队列，输入序列为1，2，3，4，分别求出一下条件的输出序列：

        1.能由输入受限得到，输出得不到。

        2.能由输出受限得到，输入得不到。

        3.输入输出都得不到，

解：应用题的话，需要一个个证明，有些多，我觉得一般都是选择和填空，因此我们采用技巧取做。

        技巧可以得到输入受限不可能得到的序列，和输出受限不可能得到的序列，随后我们让这两个求差集，即可。

输入受限得不到：

        规律：..1..2..3..4,那么4先出，则2一定不会紧跟着出来，

所以不可能得到的为：4，2，1，3 和 4，2，3，1

输出受限得不到的：
        规律：12...3..4,那么4先出。则3一定不会再12中间，因为12是紧邻着的，

所以不可能得到的为：4，1，3，2 和 4，2，3，1

随后我们根据条件去筛选即可。

(1)输入得到，输出得不到。 我们从输出得不到的里面，去筛选，输入可以得到的，

所以为4,1,3,2，因为4,2,3,1在输入受限中也得不到，所以排除。

(2)输出得到，输入得不到：我们从输入得不到的里面，去筛选，输出可以得到的，所以为：
4,2,1,3,因为4,2,3,1输出也得不到，所以排除。

(3)输入输出都得不到：因此我们，找这俩的交集，所以为：4,2,3,1

至此队列基本理论结束！以后记得常来复习。基本操作要滚瓜烂熟，先明白整体，再去记忆具体。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/861550.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

编写一个指令（v-focus2end）使输入框文本在聚焦时焦点在文本最后一个位置

编写一个指令（v-focus2end）使输入框文本在聚焦时焦点在文本最后一个位置

项目反馈输入框内容比较多时候&#xff0c;让鼠标光标在最后一个位置&#xff0c;心想什么奇葩需求&#xff0c;后面试了一下&#xff0c;是有点影响体验&#xff0c;于是就有了下面的效果&#xff0c;我目前的项目都是若依的架子&#xff0c;用的是vue2版本。vue3的朋友想要使…
阅读更多...
什么是POP3协议？

什么是POP3协议？

POP3&#xff08;Post Office Protocol Version 3&#xff09;是一个用于从电子邮件服务器获取邮件的应用层协议。以下是关于POP3的详细解释&#xff1a; 基本操作&#xff1a;使用POP3&#xff0c;电子邮件客户端可以从邮件服务器上下载电子邮件&#xff0c;并将其保存在本地。…
阅读更多...
Unity制作护盾——3、蜂窝晶体护盾

Unity制作护盾——3、蜂窝晶体护盾

Unity制作晶格护盾 大家好&#xff0c;我是阿赵。 继续来做护盾&#xff0c;这一期做一个蜂窝晶体护盾的效果。 一、效果展示 这个晶体护盾的特点是&#xff0c;整个护盾是由很多五边形和六边形的晶体构成&#xff0c;每一块晶体的颜色都在不停的变化&#xff0c;然后每一块晶…
阅读更多...
使用 Spring Boot 发送电子邮件（SMTP 集成）

使用 Spring Boot 发送电子邮件（SMTP 集成）

本文探讨了 Spring Boot 与 SMTP 的集成以及如何从您自己的 Spring Boot 应用程序发送电子邮件。 本文探讨如何从您自己的Spring Boot应用程序发送电子邮件。 是的&#xff0c;您可以拥有专用的 REST API&#xff0c;它接受电子邮件发送者和接收者的电子邮件地址、主题…
阅读更多...
【雕爷学编程】Arduino动手做（05）---热敏电阻模块之的基本参数、模块特色、电原理与使用说明

【雕爷学编程】Arduino动手做（05）---热敏电阻模块之的基本参数、模块特色、电原理与使用说明

37款传感器与模块的提法&#xff0c;在网络上广泛流传&#xff0c;其实Arduino能够兼容的传感器模块肯定是不止37种的。鉴于本人手头积累了一些传感器和执行器模块&#xff0c;依照实践出真知&#xff08;一定要动手做&#xff09;的理念&#xff0c;以学习和交流为目的&#x…
阅读更多...
SpringBoot 整合Druid

SpringBoot 整合Druid

集成Druid Druid简介 Java程序很大一部分要操作数据库&#xff0c;为了提高性能操作数据库的时候&#xff0c;又不得不使用数据库连接池。 Druid 是阿里巴巴开源平台上一个数据库连接池实现&#xff0c;结合了 C3P0、DBCP 等 DB 池的优点&#xff0c;同时加入了日志监控。 D…
阅读更多...
Chrome DevTools 与 WebSocket 数据查看失焦的问题

Chrome DevTools 与 WebSocket 数据查看失焦的问题

Chrome DevTools 在与 WebSocket 连接交互时可能会出现失焦的问题&#xff0c;这似乎是一个已知的 bug。当 DevTools 选中 WebSocket 消息时&#xff0c;如果有新的消息到达&#xff0c;DevTools 将会自动失焦&#xff0c;导致无法查看完整的消息内容。 虽然这个问题很令人困扰…
阅读更多...
C++友元函数和友元类的使用

C++友元函数和友元类的使用

1.友元介绍 在C中&#xff0c;友元&#xff08;friend&#xff09;是一种机制&#xff0c;允许某个类或函数访问其他类的私有成员。通过友元&#xff0c;可以授予其他类或函数对该类的私有成员的访问权限。友元关系在一些特定的情况下很有用&#xff0c;例如在类之间共享数据或…
阅读更多...
高斯模糊与图像处理（Gaussian Blur）

高斯模糊与图像处理（Gaussian Blur）

高斯模糊在图像处理中的用途及其广泛&#xff0c;除了常规的模糊效果外&#xff0c;还可用于图像金字塔分解、反走样、高低频分解、噪声压制、发光效果等等等等。正因为高斯模糊太基础&#xff0c;应用太广泛&#xff0c;所以需要尽可能深入认识这个能力&#xff0c;避免在实际…
阅读更多...
【css】css中使用变量var

【css】css中使用变量var

CSS 变量可以有全局或局部作用域。 全局变量可以在整个文档中进行访问/使用&#xff0c;而局部变量只能在声明它的选择器内部使用。 如需创建具有全局作用域的变量&#xff0c;请在 :root 选择器中声明它。 :root 选择器匹配文档的根元素。 如需创建具有局部作用域的变量&am…
阅读更多...
无脑——010 复现yolov8 训练自己的数据集 基于yolov8框架 使用rt detr

无脑——010 复现yolov8 训练自己的数据集 基于yolov8框架 使用rt detr

背景&#xff1a; 2023.08.09导师让调研transformer的相关论文&#xff0c;做CV的都知道transformer多么难跑&#xff0c;需要用8张GPU跑100多个小时&#xff0c;我这个小小实验室放不下这尊大佛&#xff0c;所以就找点小模型跑一跑&#xff0c;调研论文发现最新的是CO-DETR&am…
阅读更多...
【BMC】OpenBMC开发基础3：引入新的开源配方

【BMC】OpenBMC开发基础3：引入新的开源配方

引入新的开源配方 前面介绍了如何在OpenBMC中通过新建配方引入自己的程序&#xff0c;也介绍了如何修改原有的程序&#xff0c;下面要介绍的是如何引入开源的新程序&#xff0c;这在OE系统上是很方便的&#xff0c;重点就在于引入新的配方。 OE为了方便开发者使用&#xff0c…
阅读更多...
到 2030 年API 攻击预计将激增近 1000%

到 2030 年API 攻击预计将激增近 1000%

导读云原生应用程序编程接口管理公司 Kong 联合外部经济学家的最新研究预计&#xff0c;截至 2030 年 API 攻击将激增 996%&#xff0c;意味着与 API 相关的网络威胁的频率和强度都显着升级。 这项研究由 Kong 分析师和布朗大学副教授 Christopher Whaley 博士合作进行&#x…
阅读更多...
Maven进阶2 -- 私服（Nexus）、私服仓库分类、资源上传和下载

Maven进阶2 -- 私服（Nexus）、私服仓库分类、资源上传和下载

目录 私服是一台独立的服务器&#xff0c;用于解决团队内部的资源共享与资源同步问题。 1.Nexus Nexus是sonatype公司的一款maven私服产品。 下载地址 启动 nexus.exe /run nexus 访问 & 登录 2.私服仓库分类 3.资源上传和下载 本地仓库上传和访问资源需要进行配置。…
阅读更多...
stm32项目（8）——基于stm32的智能家居设计

stm32项目（8）——基于stm32的智能家居设计

目录 一.功能设计 二.演示视频 三.硬件选择 1.单片机 2.红外遥控 3.红外探测模块 4.光敏电阻模块 5.温湿度检测模块 6.风扇模块 7.舵机 8.WIFI模块 9.LED和蜂鸣器 10.火焰传感器 11.气体传感器 四.程序设计 1.连线方式 2.注意事项 3.主程序代码 五.课题意义…
阅读更多...
学习pytorch 3 tensorboard的使用

学习pytorch 3 tensorboard的使用

tensorboard的使用 1. 安装2. add_scalar 查看函数图形3. 查看结果4. add_image() 查看训练步骤中间结果的图片 1. 安装 pytorch conda环境 pip install tensorboard pip install opencv-python2. add_scalar 查看函数图形 常用来查看 train val loss等函数图形 from torch…
阅读更多...
Mr. Cappuccino的第60杯咖啡——Spring之BeanFactory和ApplicationContext

Mr. Cappuccino的第60杯咖啡——Spring之BeanFactory和ApplicationContext

Spring之BeanFactory和ApplicationContext 类图BeanFactory概述功能项目结构项目代码运行结果总结 ApplicationContext概述功能MessageSource&#xff08;国际化的支持&#xff09;概述项目结构项目代码运行结果 ResourcePatternResolver&#xff08;匹配资源路径&#xff09;概…
阅读更多...
基础实验篇 | QGC实时调整控制器参数实验

基础实验篇 | QGC实时调整控制器参数实验

PART 1 实验名称及目的 QGC实时调整控制器参数实验&#xff1a;在进行硬件在环仿真和真机实验时&#xff0c;常常需要在QGC地面站中观察飞行状态&#xff0c;并对控制器参数进行实时调整&#xff0c;以使得飞机达到最佳的控制效果&#xff0c;但是&#xff0c;在Simulink中设…
阅读更多...
网络编程的一些基础知识

网络编程的一些基础知识

什么是协议 协议就是一种网络交互中数据格式和交互流程的约定，通过协议，我们可以与远程的设备进行数据交互，请求或者完成对方的服务（可以认为协议就是一种语言） 什么是端口和端口监听 在Internet上，各主机间通过TCP/IP协议发送和接收数据包，各个数据包根据其目的主机…
阅读更多...
15.3.2 【Linux】系统的配置文件：/etc/crontab,/etc/cron.d/*

15.3.2 【Linux】系统的配置文件：/etc/crontab,/etc/cron.d/*

这个“ crontab -e ”是针对使用者的 cron 来设计的&#xff0c;如果是“系统的例行性任务”时&#xff0c; 该怎么办呢&#xff1f;是否还是需要以 crontab -e 来管理你的例行性工作调度呢&#xff1f;当然不需要&#xff0c;你只要编辑/etc/crontab 这个文件就可以。有一点需…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023