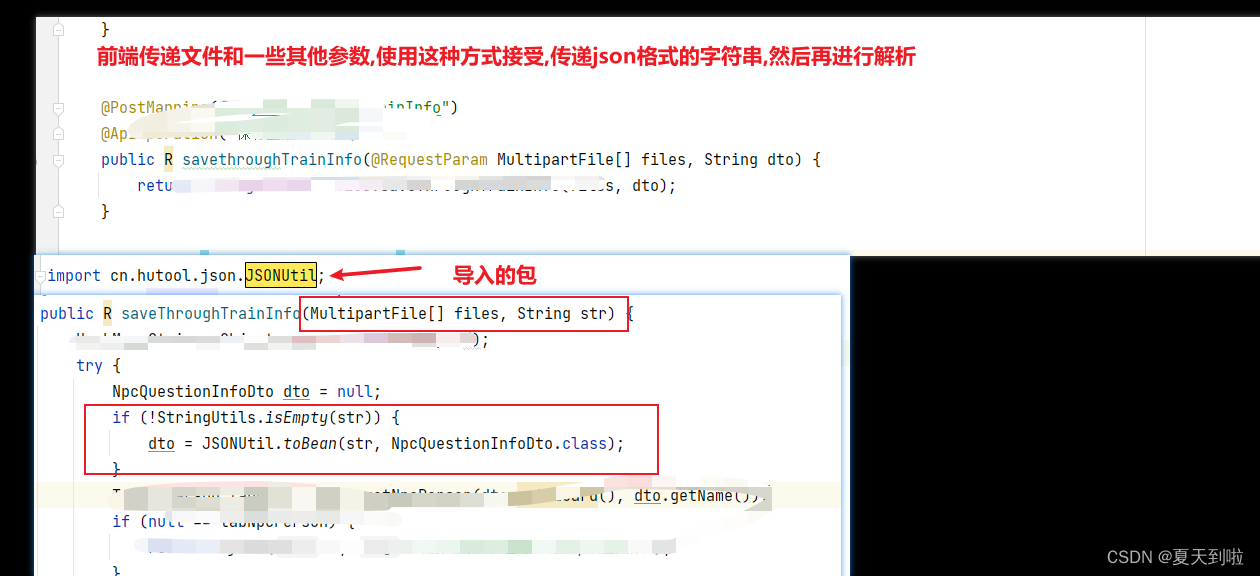
目录
1. 前言
1.1 Minimax
1.2 剪枝
1.3 蒙特卡洛树搜索
1.4 为什么随机走子会可行呢?
2. vanilla Monte Carlo tree search
3. UCT-based trade-off between exploitation and exploration
4. MCTS基本算法流程
5. Efficiency Through Expert Policies
6. Efficiency Through Value Approximation
1. 前言
众所周知,像围棋、国际象棋等这一类两人对抗性游戏(discrete, deterministic games with perfect information)项目的智能agent或者说bot的实现的最关键算法之一是蒙特卡洛树搜索(Monte Carlo Tree Search)。

1.1 Minimax
在双人对弈游戏中,某一方下子时,会考虑所有可能落子,针对每一落子考虑对手所有可能的应手,针对对手的每种可能应手进一步考虑自己的应手,这样一直考虑下去,这个过程实际上就是在构建一棵搜索树进行搜索。。。理论上如果可能计算到终局(即构建完整的搜索树),就可以每一步都采取理论上最优的落子策略(不一定能够战无不胜,取决于游戏类型)。这个过程其实就是Minimax search algorithm(极小化极大搜索算法)的执行过程。
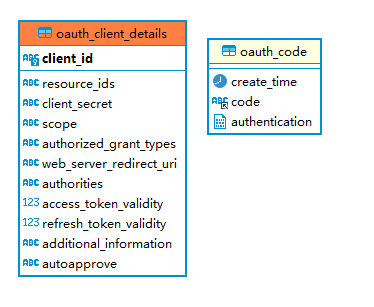
像Tic-tac-toe这样的小规模游戏,现代计算机可以轻松地从一开始就构建出所有可能棋盘局面构成的搜索树,从而可以给出理论最优解。因此基于minimax搜索算法可以很容易地设计出unbeatable tic-tac-toe agent/bot。之所以说是unbeatable而不是战无不胜的,是因为Tic-tac-toe游戏是一个有先手优势的游戏,假定先手方能下出最优解,后手方就不可能战胜先手方,最多只能下成平局。理想棋手与非理想棋手之间的对弈结果关系如下所示:
但是,对于像象棋(中国象棋、国际象棋、日本将棋等)或者围棋,分支系数太大,搜索树的规模呈指数方式快速增长,而且深度可能上百层(一局围棋的手数可以轻松到达2~300以上)。构建完整的搜索树是完全无法想象的,无论从存储资源还是从计算时间来说。
关于minimax,有兴趣者可以参考TicTacToe:Minimax-Agent以及人机对弈python实现
1.2 剪枝
解决以上搜索树规模爆炸问题的关键技术是剪枝,即通过忽略搜索树的某些部分来缩减搜索空间。
搜索树是2维的,它具有宽度和深度。
宽度是指某个特定棋局(注意,棋局有时是指一局棋,有时是指一个盘面状态,当前棋盘上的局面的意思。根据上下文应该可以好无歧义地判断是指那种意思)下可能动作的数据(常称分支系数,branching factor)。
深度是指从某个棋局开始到可能的棋局终局状态的手数(或者说回合数。但是通常来说两个各下一手称为一个回合)。
当然,这两个数值对于每一个棋局来说都可能是不同的。
剪枝可以从深度和宽度两个方面来考虑,相应地有两种典型的剪枝技术:
- 一是基于棋局评估函数来减少搜索深度;
- 另一是用于减少搜索宽度的alpha-beta剪枝;
1.3 蒙特卡洛树搜索
剪枝(无论是深度还是宽度)技术的性能最终决定对棋局的评估,而对于围棋来说,棋局评估是一件非常困难的事情。蒙特卡洛树搜索(MCTS)为我们提供了一种有效的方法,不需要依赖于什么高深的游戏策略,也不需要利用游戏特定的启发式规则,通过模拟随机棋局的方式来进行棋局好坏的评估,并据此进行落子选择。
通常把模拟进行的每一个随机棋局称为一次推演(rollout)。
1.4 为什么随机走子会可行呢?
2. vanilla Monte Carlo tree search
以下以Tic-Tac-Toe游戏为例来说明基本的MCTS算法。
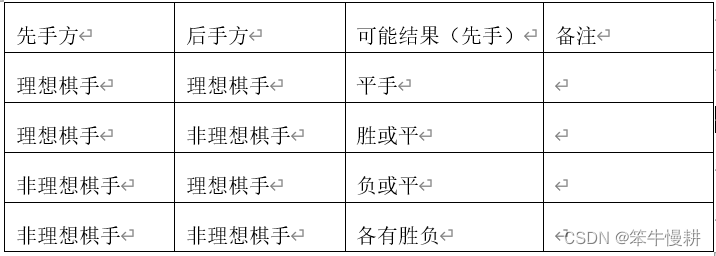
MCTS算法的处理从某个棋局(以下记为s0)开始,棋手在s0棋局下有若干种可能的落子点(可以理解为从一个actions set \mathscr{A}\中选择可能的动作)。每一种可能的落子导向下一个棋局,对应于搜索树中s0节点的子节点。尝试每一种可能的动作即对应蒙特卡洛树搜索树的扩展(expanding),这样一步步(交替尝试双方的可能的落子)深入下去直到终局的过程,就是构建蒙特卡洛搜索树的过程。
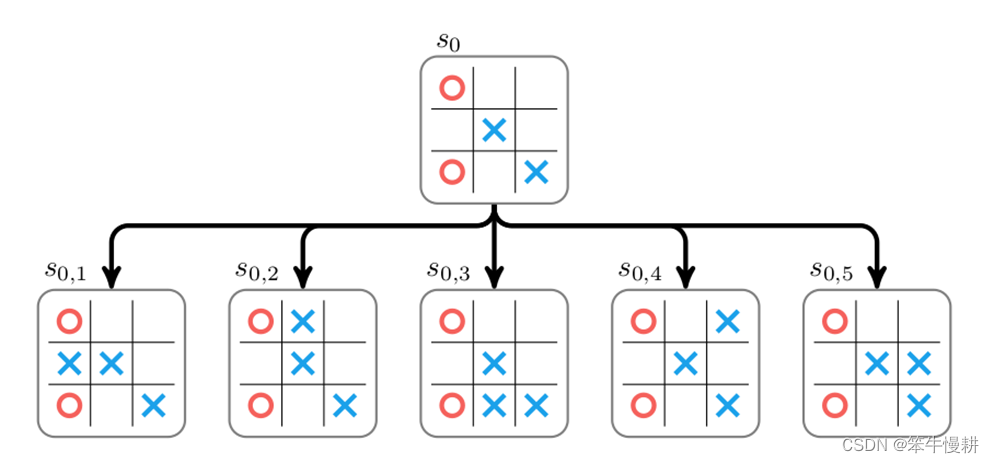
上图为从某个盘面状态s0出发进行搜索的示例。在该状态下下一手有5种可能,分别对应以上搜索树的5个子节点(每个子节点对应于某个下一手下完后所到达的状态)。为了选择最佳的一手,必需给每个这个每个子节点赋予一个分数(score,以下图中用W表示),然后就可以根据分数高低来选择(确定性地,选择分数最高的一手;或者概率性地进行选择,分数高的被选中的概率更高)下一手。这个可以通过从该子节点所代表的棋局出发,通过随机走子(random rollout)直到终局,并根据胜负结果来对该子节点进行打分(获胜即给+1分,负则给-1分,平局则得0分)。
本例中,考虑从出发经过随机走子到达终局,如果当前落子方获胜即给+1分,负则给-1分,平局则得0分。当然,由于是随机走子,一局、两局的结果可能并不足以代表真实的情况。实际上,需要从
出发经过随机走子若干局后得到的总分数(或者平均分数)作为
的分数(可以理解为在当前局面下当前落子方的胜率)。
都进行了随机走子后可以得到各节点对应的分数。然后,就可以根据这个分数进行落子选择。
每个节点存储的不仅仅有分数,还有从该节点出发所搜索过的棋局数N。
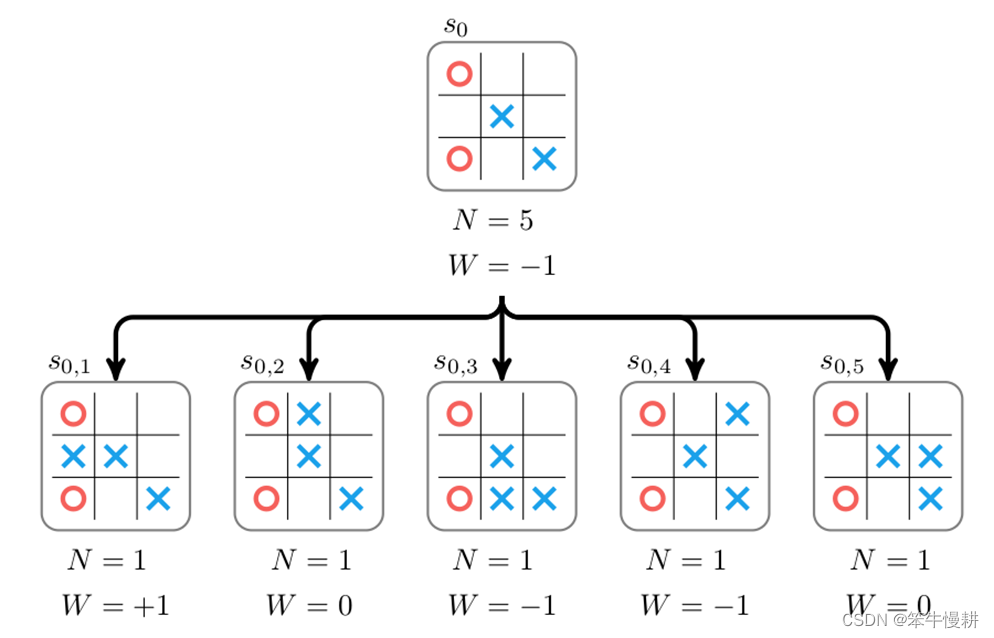
经过棋局推演(针对每个子节点各试走了一局)后,假设我们得到的数据{N,W},然后再通过回溯就可以相应得到
的数据(由于是基于
的分数进行落子选择,看似我们并不需要更新
的数据?其实不然,更新
的数据至少有两个用途:
(1) 总试走子对局数用于如下UCT-based算法需要的\N_p\;
(2) 可以根据{W,N}计算出当前状态下的胜率(可以是当前状态下的总体胜率,也可以是当前状态下棋手下出最佳下一手时的胜率)。在bot对弈或者bot-human对弈时的直播通常会显示这个信息。
在蒙特卡洛树搜索算法中,大量地重复以上处理(树的扩展,棋局推演。。。),当试推演的棋局数足够多而且对各种不同棋局的覆盖度足够高时,所产生的结果就有可能统计充分地(statistically sufficiently)给出足够好的棋局评估结果,并据此做出合理的落子决策。
一般来说,MCTS算法包含以下4个基本步骤:
- selection,选择合适的叶子节点进行进一步扩展
- expansion, 针对选定的叶子节点进行搜索树扩展
- evaluation, 评估所扩展出来的新的叶子节点所代表的棋局
- backup,基于将评估结果通过回溯更新整个蒙特卡洛搜索树
与minimax一样,MCTS算法也同样需要基于剪枝来缩减搜索空间。前面剪枝技术的最大难点在于对棋局的评估,那么MCTS是如何解决棋局评估问题的呢?
3. UCT-based trade-off between exploitation and exploration
在改进的MCTS算法中,采用基于UCT的选择算法来实现探索(exploration)和利用(exploitation)之间的折衷。针对每一个节点,计算其UCT(Upper confidence tree) score如下:
其中:
: the number of visit counts for the parent node
: trade-off factor. c越小表示越偏向优先选取既得平均分数高的子节点;c越高就表示优先选择访问次数少的子节点。这一策略是强化学习中经典的trade-off-between-exploitation-and-exploration策略。右边第一项代表exploitation,第二项则代表exploration。
针对以上例子计算各子节点的UCT后更新如下。
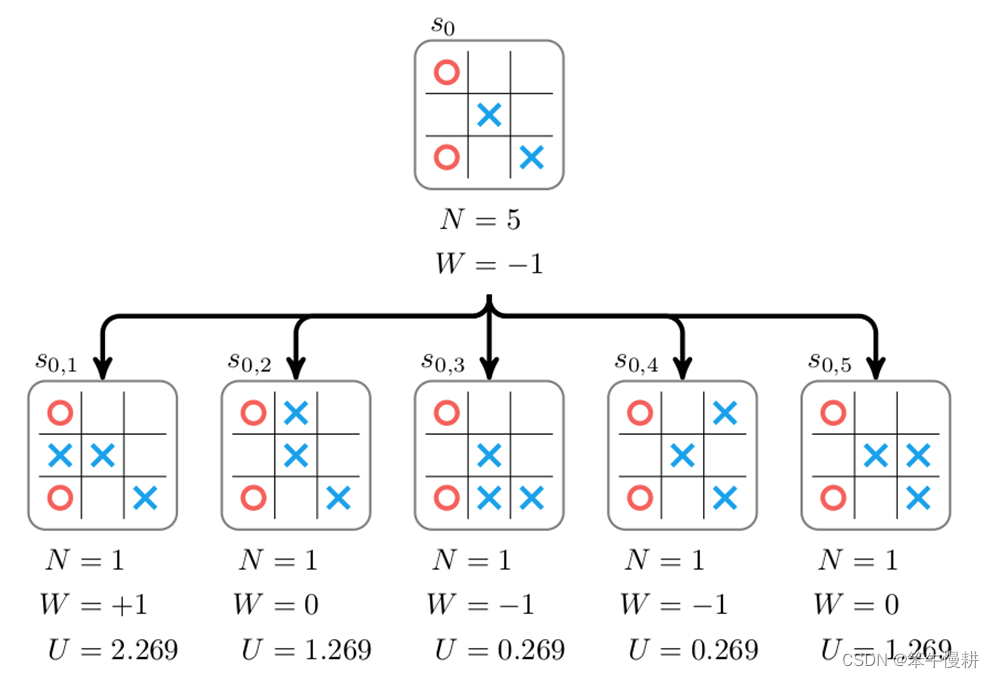
如上图所示,很显然,最左边的子节点为最优节点(当出现平局时可以随机选择一个或者确定性选择—比如说其中序号更小—某一个均可)。针对这个节点进一步进行展开,并同样将其结果进行回溯更新得到如下图所示:

这里需要注意的是,由于是对抗性游戏,双方轮流落子。胜负关系从对局双方来看是反的。在统计胜负结果计数时要注意始终站在当前搜索树根节点\s_0\的该当落子者的立场来进行统计。
不断重复以上MCTS迭代直到退出条件满足(比如说,设定每次MCTS处理的总的rollout局数N。由于以上基于UCT的选择机制,各子节点访问次数可能并不均等,有的子节点多一些,有的子节点少一些),蒙特卡洛搜索树会不断扩展生长,如果我们的选择机制足够好的话,就有可能以尽量小的代价对所有可能而且有效的“下一手”进行充分的探索和覆盖(同时,有效地忽略了那些价值较低的选项。通俗一点说,就是做到“好钢用在刀刃上”)。然后,就可以基于搜索结果选择最合理的下一手。比如说,如果我们通过从s0出发的MCTS搜索得到了以下结果,那很显然下一手应该选择s0,1:

4. MCTS基本算法流程
总结一下,面向对弈游戏的MCTS基本算法流程如下所示(示意):
- 以
为根节点初始化一个搜索树,并初始化
的数据:{N=0, W=0}
- 从
往下搜索,找到一个能够添加子节点的叶子节点
- 往下搜索过程中,子节点选择发生在同一层,同一层之间的比较选择可以是随机的,也可以是基于UCT的
- 对该叶子节点添加一个子节点,并从该子节点开始进行(随机或者非随机)棋局推演(rollout)
- 根据棋局推演结果回溯更新当前子节点以及其所有祖先节点的信息,N、W、UCT、etc
- 如果满足rollout退出条件,前进到(6);否则,返回(2)。rollout退出条件有以下可能的选择:
- Rollout退出条件可以是到达了预设的最大rollout数
- 搜索时间到达了预设时间(即发生了timeout)
- Others
- 根据
的各子节点的分数选择其中最优子节点进行实际落子
其中,影响效率的关键就在于第2步、第3步选择展开(以进行rollout)的叶子节点的处理。
5. Efficiency Through Expert Policies
国际象棋和围棋的分支系数非常大,在一个局面下,可以选择落子点非常多,这使得充分地对未来可能的对局状态进行探索非常困难。国际象棋的可能棋局数据估计为,而围棋(标准的19路棋盘)的可能棋局数高达
。与之相比,TicTacToe游戏只有5478种而已。所以,对于国际象棋或者围棋来说,完全随机的MCTS(vanilla MCTS)是不够的,还需要有更进一步的策略用于提高搜索效率。
假定我们有一个已知的专家策略(expert policy),能够给出专家(职业选手)在特定状态下采取某一落子的可能性
,如下图所示:
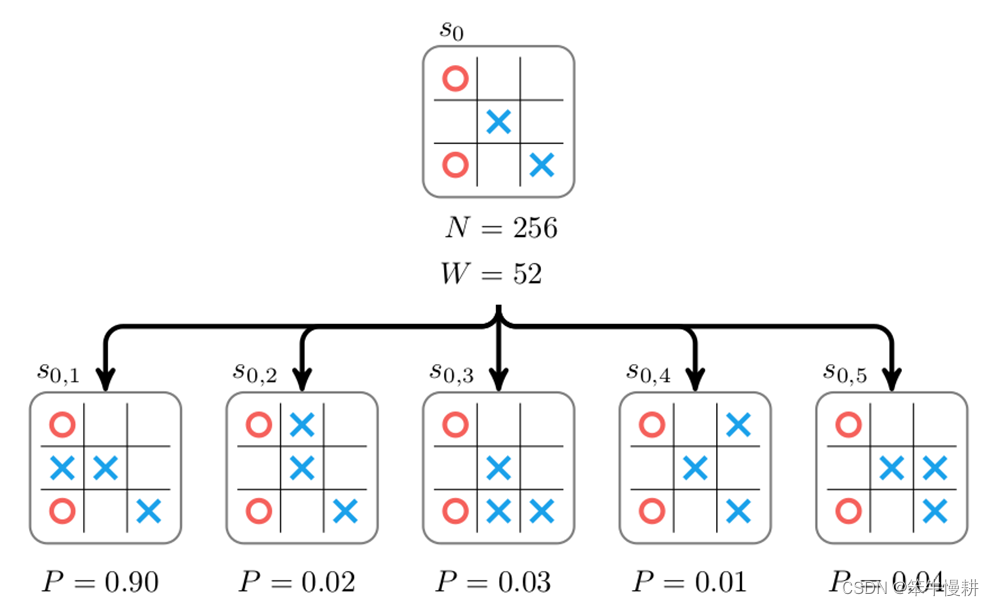
这样的话,问题就简单了。只要这个策略足够好,落子时只要查询一下所有可能的子节点所对应的概率取其最大值(或者以概率的方式进行采样)就可以了。但是,构造一个专家策略非常困难,验证一个专家策略是否最优同样非常困难。
幸运的是,我们可以对以上MCTS方案进行一定的微调,并用于进行策略提升。在这个变化版本中,每个节点仍然存储基于策略的概率信息\P_i\,而这个概率信息又被用于调节节点的用作选择基准的UCT score。Deepmind所使用的probabilistic upper confidence tree score如下所示:
与前述的基本的UCT score的区别在于(1)右边第2项多了一个概率乘性因子;(2)根号里面的分母加1。概率乘性因子Pi体现了“expert policy”对MCTS过程的节点选择的影响。\P_i\初始化为均一分布(uniform distribution)时则退化为原来的基本UCT-score。新的MCTS过程的节点选择将在以下三方面取得折中:
- 分数高者得到更多机会
- 访问次数少者得到更多机会
- “expert policy”认为更可能的子节点得到更多机会
如果专家策略足够好的话,MCTS就可以更加聚焦于比较有利的棋局状态的演化探索;反之,如果专家策略不好的话,就会导致MCTS聚焦与比较不利的棋局状态的演化探索。但是,不管怎样,只要搜索的量足够大的话,最终,都能够收敛于相同的结果,即UCT最终都是主要由来决定。
但是当搜索资源受限,即只能进行有限的搜索时,好的专家策略就能给出(概率意义上)更好的结果,自然也就能使得(采用该策略的)bot更强大。
6. Efficiency Through Value Approximation
另外一种提高效率的方法是直接基于价值近似的方法。假定有一个价值近似函数\ \hat{W}(x)\,(不需要进行rollout,也就是根本不进行MCTS)直接输入当前盘面状况价值评估(比如说代表当前局面的胜率)。如果该函数是一个很好的价值近似函数,而且其执行速度比rollout要更快的话,那么就可能用折中策略实现一个又快又强大的bot。
需要注意的是价值近似函数\ \hat{W}(x)\与前面提及的expert policy \Pi(a|s)\是不一样的。后者代表的是专家在当前局面下的落子概率,而\ \hat{W}(x)\直接代表当前局面的价值(比如说胜率)。虽然专家落子概率大的点通常意味着落子与该点能够获得更高的胜率,在理想条件下两者应该是代表相同的信息。但是,在有现实约束的条件下,两者不是完全一回事。
价值近似与expert-policy可以并行使用以加速MCTS。但是,根本的问题是,如何构建或者获得expert-policy和价值近似函数呢?
Deepmind给出的答案是,没有现成的expert-policy和价值近似函数,通过self-play(左右手互博)以及深度强化学习来自己琢磨出expert-policy和价值近似函数来。事实上,Deepmind通过AlphaGoZero证明了用拿来主义从人类棋手那里总结出来的expert-policy不好使,把bot宝宝带歪了。。。完全脱离人类经验自己从零开始学习使得AlphaGoZero的实力(相比之前的AlphaGo-Fan、Lee、Kejie以及后来的Master)获得了飞跃式的发展。
Coming soon:
AlphaGo Zero是如何训练的?
MCTS agent for Tic-Tac-Toe implementation (python, pytorch)
DIY Go agent implementation ...
Reference:
[1] AlphaGo Zero – How and Why it Works – Tim Wheeler (hibal.org)
[2] 《深度学习与围棋》,人民邮电出版社