0 提纲

6.1 矩阵分解
6.2 全连接 BP 神经网络
6.3 卷积神经网络
6.4 LSTM
6.5 Transformer
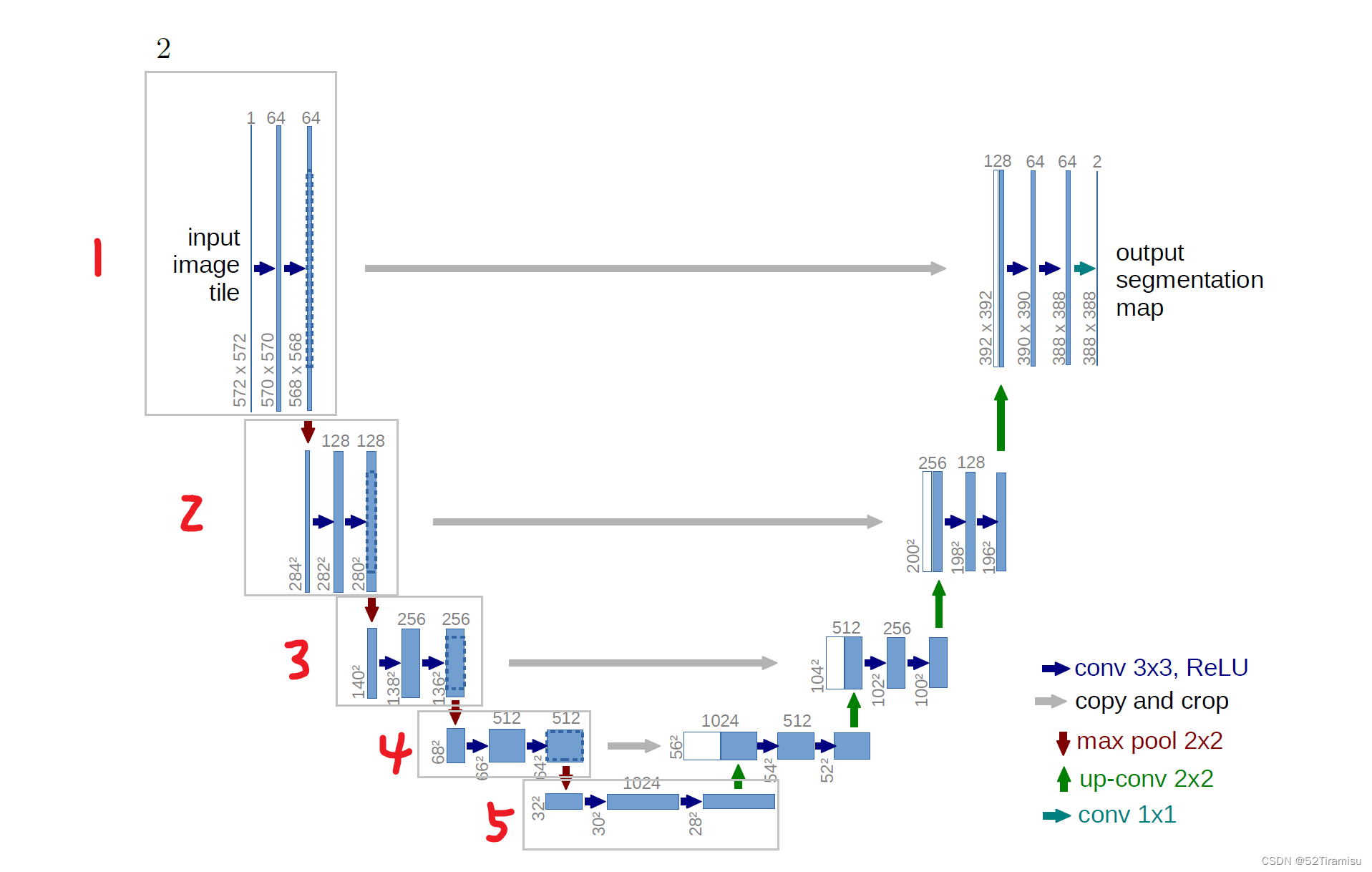
6.6 U-Net

1 矩阵分解

把稀疏矩阵分解成两个小矩阵的乘积, 恢复后的矩阵用于预测.

1.1 基本概念

矩阵分解是使用数学应对机器学习问题的一类典型而巧妙的方法.
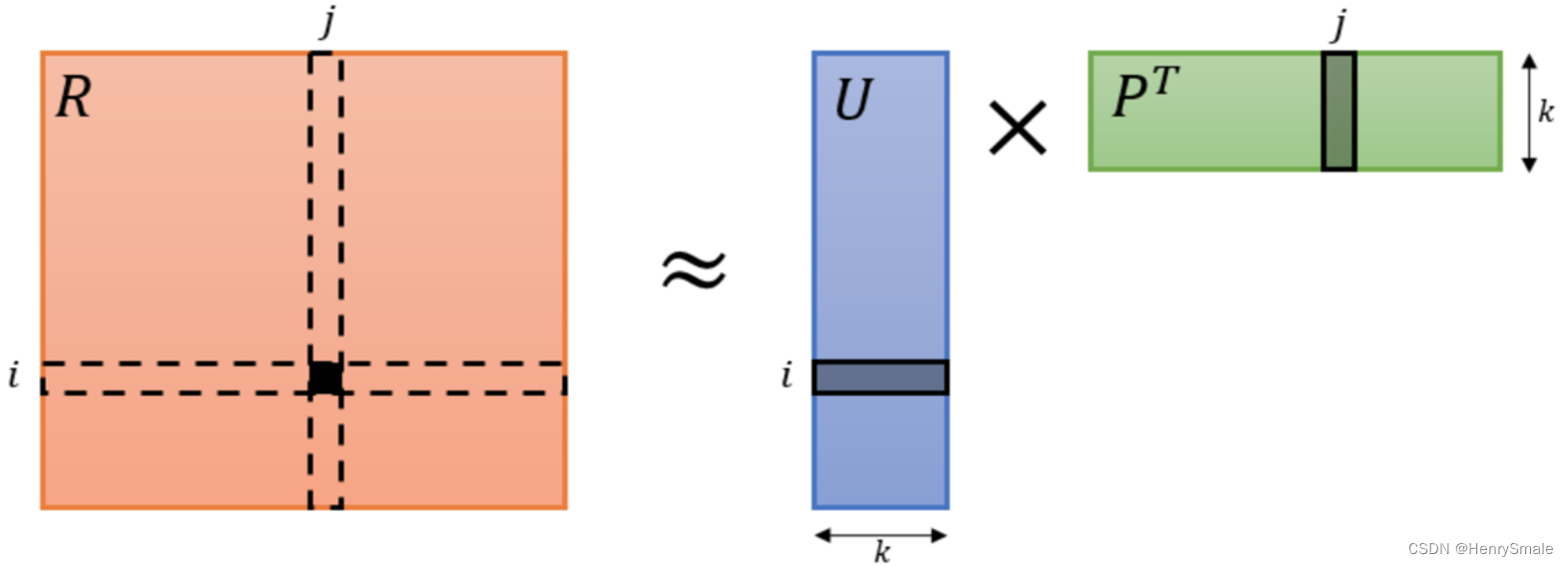
矩阵分解是把将一个$m\times n$矩阵 $\mathbf{R}$ 分解为：
$m\times k$ 矩阵$\mathbf{P}$ 和 $n\times k$ 矩阵$\mathbf{Q}$；
使得 $\mathbf{R}\approx {\mathbf{P}}^{\mathbf{T}}\mathbf{Q}$, 其中 k ≪ min ⁡ { m , n } k≪\min\{m,n\} k≪min{m,n}.

有两种常见的情况:

• 非负矩阵分解 要求两个个矩阵的元素均为非负值. 这样在其应用中才有良好的解释.
• 稀疏矩阵分解 要求$\mathbf{R}$为稀疏矩阵, 即其元素绝大多数值为 0.

1.2 稀疏矩阵分解的应用: 推荐系统

问题引入: 电影网站有 $m>10^6$个用户, 以及$n>10^4$部电影. 由于每个用户仅看了少量 (通常少于$10^3$, 很多少于$10^2$) 电影, 所以评分矩阵$\mathbf{R}=(r_{ij}{)}^{m\times n}$是一个稀疏矩阵, 其中$r_{ij}=0$ 表示用户没看这部电影, 而1~5分表示从最不喜欢到最喜欢. 现在需要预测用户对电影的评分, 也就是将0替换成具体的分数.
问题定义:

• 输入：评分矩阵$\mathbf{R}$, 秩$k$;
• 输出：用户偏好矩阵$\mathbf{P}\in {\mathbb{R}}^{k\times m}$, 矩阵$\mathbf{Q}\in {\mathbb{R}}^{k\times n}$.
• 优化目标：
  $$\min ||\mathbf{R}-{\mathbf{P}}^{\mathbf{T}}\mathbf{Q}||$$

这里计算优化目标的时候, $r_{ij}=0$ 的数据点并不参加计算. 这样, 当把两个小矩阵 (也称用户子空间与项目子空间, subspace) 求到后, 直接相乘 $\mathbf{R}\prime ={\mathbf{P}}^{\mathbf{T}}\mathbf{Q}$, 以前$r_{ij}=0$的地方, $r_{ij}^{\prime }=0$ 就有了值, 这就是预测评分.
有没有觉得特别神奇?

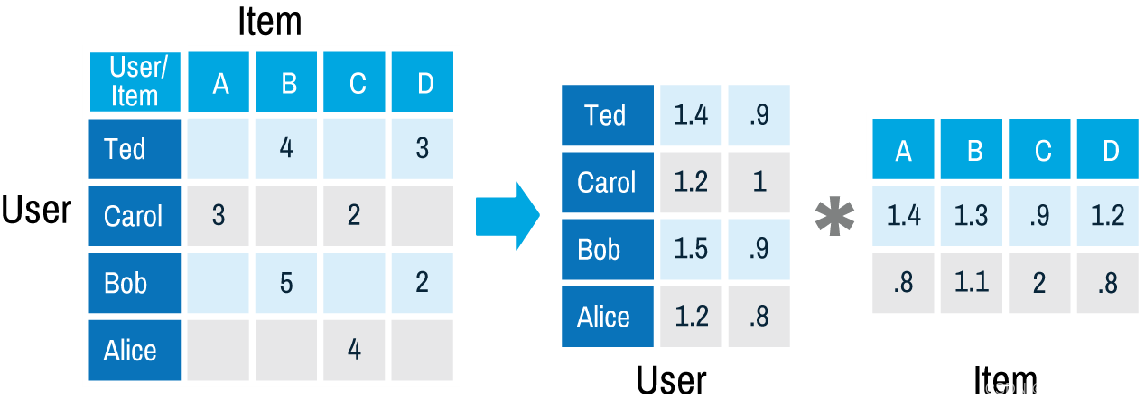
1.3 推荐系统：小例子

其中用 − 表示 0, 更清楚一些


当然, 这个方案并不完美, 如

• $\mathbf{P},\mathbf{Q}$ 有些元素为负值, 解释起来有点难受. 可以考虑非负矩阵分解.
• ${\mathbf{R}}^{\prime }$有些元素不在正常范围[1,5], 可以强行让越界的数据回到边界.

1.4 SVD: 解决过拟合

为了避免过拟合, 优化目标上还可以加上正则项, 如：
$$\min ||\mathbf{R}-{\mathbf{P}}^{\mathbf{T}}\mathbf{Q}||+\lambda (||\mathbf{P}|{|}^2+||\mathbf{Q}|{|}^2)$$
参考论文：Ruslan Salakhutdinov and Andriy Mnih, Probabilistic Matrix Factorization, NIPS, 2007.

1.5 子空间的物理意义

从推荐系统的角度, 每个用户对应于 $1\times k$ 的向量, 这是对用户偏好的高度压缩;
每个项目也对应于$1\times k$ 的向量, 这是对项目属性的高度压缩.
这 k 个偏好和属性形成一一对应. 例如, $k=3$:

• 第 1 维表示用户对颜值的关注度 (对应的是电影男女主的帅气与漂亮程度);
• 第 2 维表示用户对情节的关注度 (对应的是剧本的逻辑性);
• 第 3 维表示用户对视觉震撼度的要求 (对应的是电影场景与特效).

需要注意, 这里只是强行解释, 在现实世界中, 而这 k 个偏好 (属性) 的涵义可能无法表达出来, 因此我们称之为隐藏变量 (latent variable).
例:

• 用户向量为 [ 0.8 , 0.1 , 0.1 ] 表示他是个颜控, 而电影向量为 [ 0.1 , 0.7 , 0.2 ]表示它更注重情节, 两者求内积导致评分低.
• 如果电影向量为 [ 0.9 , 0.01 , 0.01 ]则更好地迎合该用户的品味. 内积居然可以起到这种匹配的作用.

假设 $m=10^6$, $n=10^4$, $k=10$, 原始矩阵 (如果不考虑稀疏矩阵的压缩存储) R 需要 $10^{1}0$存储空间；
而 P与 Q 的存储空间分别是 $10^7$ 与 $10^5$. 从这个意义上来说, 数据的压缩比达到了约 1 : 1000.
与数据压缩相对应的是

• 坏消息: 信息损失. R′无法对 R 完全拟合, $k$ 越小, 拟合能力越差.
• 好消息: 数据平滑. 我们经常假设原数据就是有噪声的, 矩阵分解并恢复后, 可以将它们去掉. 甚至可以将一张人脸图片进行矩阵分解与恢复, 达到美颜去痘的效果.

1.6 Bias-SVD：偏置

偏置部分主要由三个子部分组成：

• 训练集中所有评分记录的全局平均数$\mu$;
• 用户偏置$b_u$，独立于物品特征的因素，表示某一特定用户的打分习惯（批判性用户、乐观型用户）;
• 物品偏置$b_i$，独立于用户兴趣的因素，表示某一特定物品得到的打分情况（好片、烂片）;
  $$b_{ui}=\mu +b_u+b_i$$
  

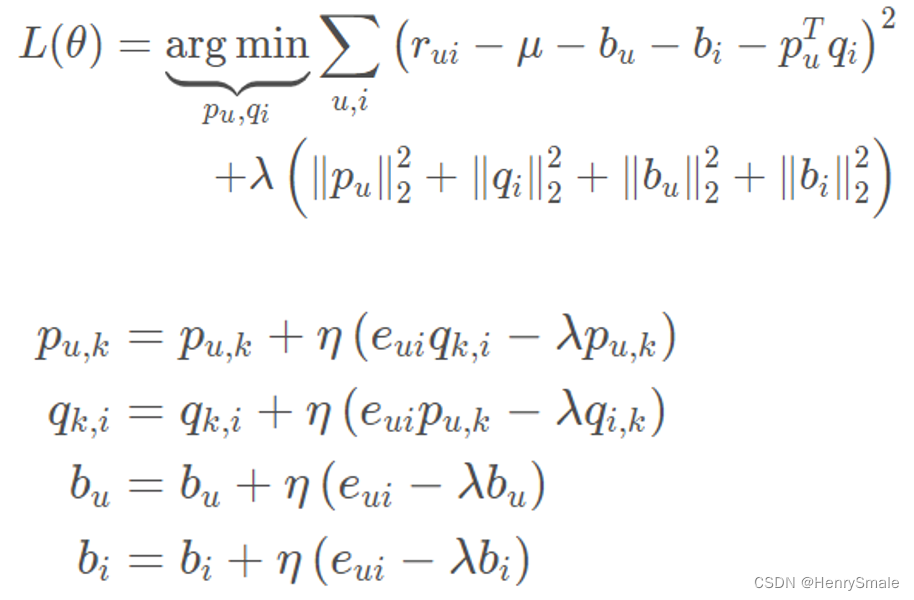
1.7 带情感分析的矩阵分解(SBMF)

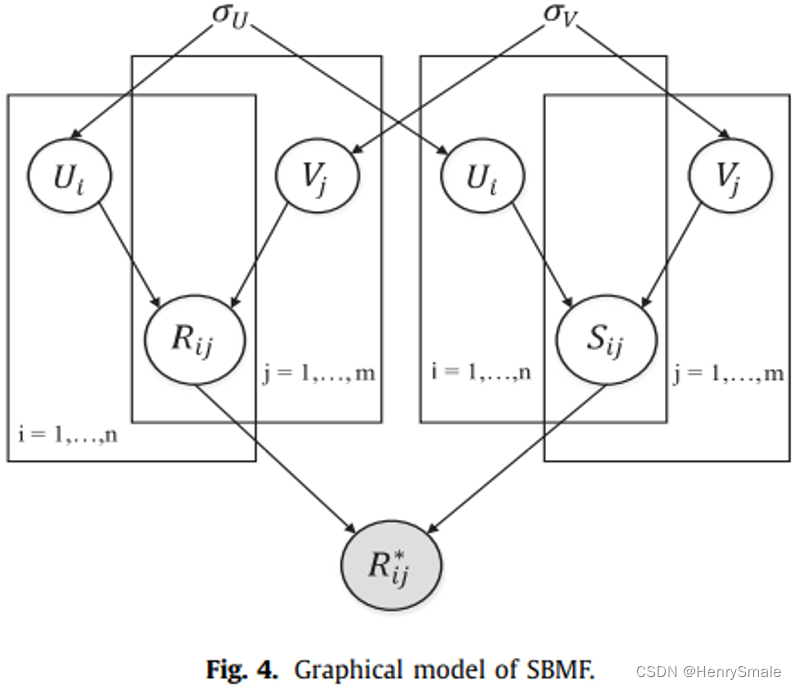
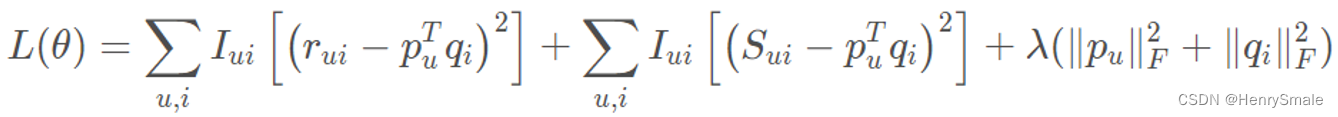
参考论文：Sentiment based matrix factorization with reliability for recommendation. Expert Systems with Applications. (2019) 249-258

1.8 带情感分析的矩阵分解(SBMF+R)

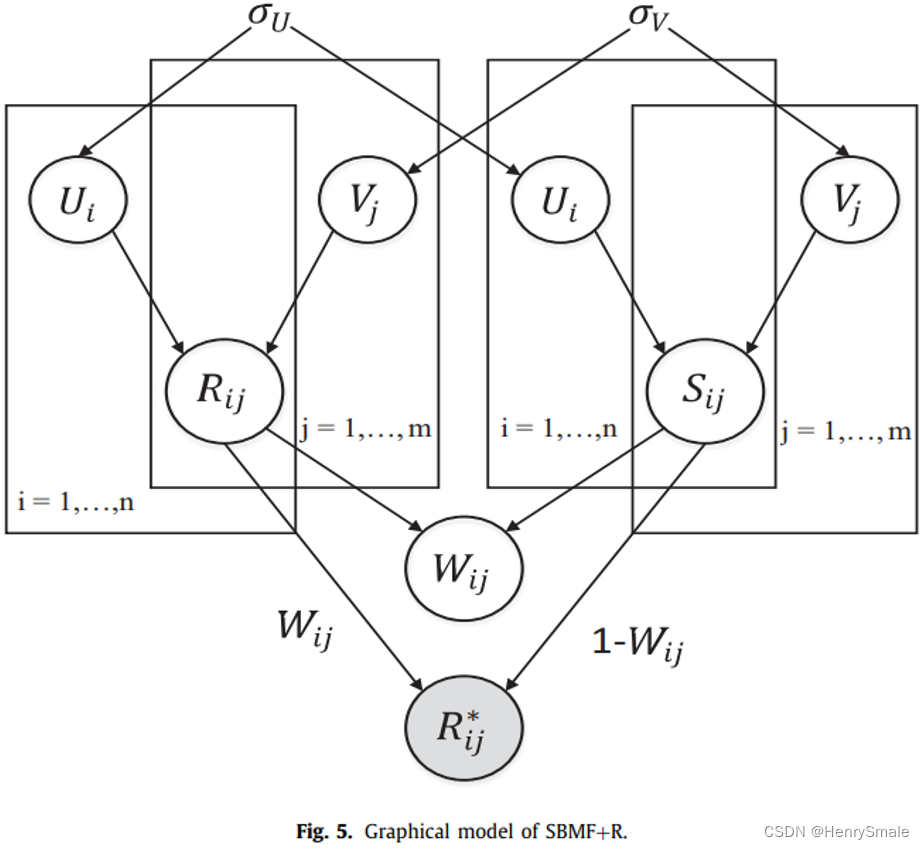
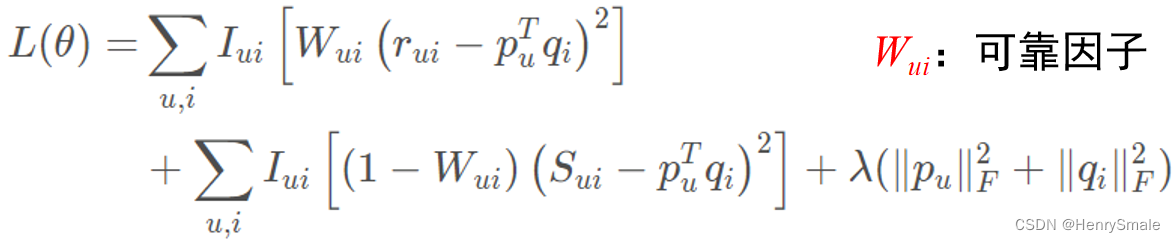
2 全连接 BP 神经网络

线性 + 激活函数, 人工神经网络是万能的函数逼近器.

2.1 BP 神经网络的结构

BP (Backpropagation ) 神经网络是一个万能的函数模拟器.
所有的神经网络, 本质都是特征提取器 – 斯.沃索地.

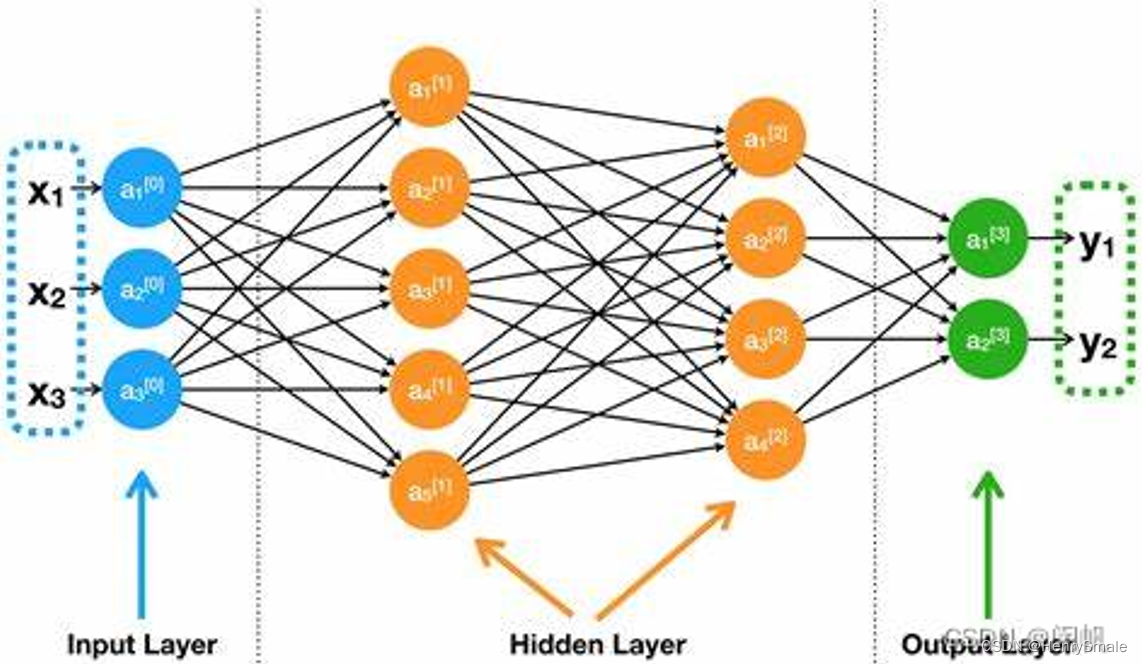
下图给出一个四层神经网络.

• 输入层有 3 个端口, 表示数据有 3 个特征;
• 第一个隐藏层有 5 个节点, 表示从 3 个特征提出了 5 个新的特征, 每个新特征都是前一特征的加权和 (线性模型);
• 第二个隐藏层有 4 个节点, 表示从上一层的 5 个特征提出了 4 个新的特征;
• 输出层有 2 个节点, 表示从上一层的 4 个特征提出了 2 个新的特征.

神经网络可以解决各种机器学习问题:

• 假设这里应对的是二分类问题, $y_1$对应于负例, $y_2$对应于正例, 那么, $y_1\ge y_2$时, 就预测为负例, 否则预测为正例.
• 对于$k$ 个类别的多分类问题, 输出端口数设置为$k$.
• 对于回归问题, 输出端口设置为 1.

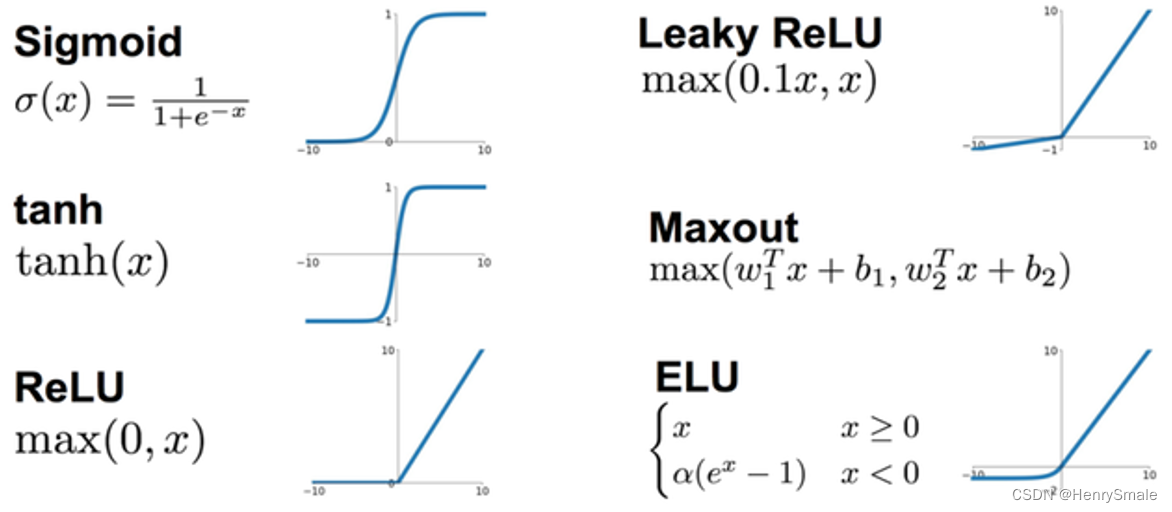
2.2 激活函数

仅仅是线性方案, 也就相当于logistic 回归 的水平, 肯定不能让 BP 神经网络达到现有的高度. 而且, 仅仅是线性方案, 多层与两层没有区别, 因为三层的 $\mathbf{X}{\mathbf{W}}_1{\mathbf{W}}_2$可以替换为两层的 $\mathbf{X}{\mathbf{W}}_3$, 其中 ${\mathbf{W}}_3={\mathbf{W}}_1{\mathbf{W}}_2$.

• 激活函数将加权和变成另一个值, 如 f ( x ) = max ⁡ { 0 , x } f(x) = \max\{0, x\} f(x)=max{0,x}
• 这种简单到令人发指的函数, 就可以改变线性特点.
• 于是, 神经网络就变成了万能的函数逼近器, 也就是说, 任意函数都可以用一个神经网络来逼近, 参见 https://zhuanlan.zhihu.com/p/162769333

2.3 与 PCA 的联系与区别

联系: 都是进行特征提取.
区别:

• PCA 的特征提取是无监督的, 神经网络一般是有监督的;
• PCA 的特征提取有理论依据, 神经网络的连边使用一些随机的初始权重, 然后不断调整;
• PCA 的特征提取数量有理论依据, 神经网络每层节点数量 (特征数量) 是人为设置的超参数, 连激活函数的选取也是人为的.

2.4 深度学习与宽度学习

如果数据集比较小, 特征比较少, 则应该使用较少的层数, 以及较少的节点数.
如果数据集比较大, 特征比较多, 则应该使用较多的层数, 以及较多的节点数. 所以形成了深度学习. 换言之, 深度学习特别“吃”数据, 数据量小了就别玩, 去搞搞SVM之类的小样本学习吧.

宽度学习是指隐藏层的节点数非常多, 理论上已经证明, 宽度学习与深度学习是等价的. 我认为原因在于: 由于神经网络初始权重设置的随机性, 宽度学习提取的特征非常多, 总有几个是合适的.

2.5 关于调参师

有些人诟病做神经网络 (特别是应用) 就是当网络调参师: 几层，什么激活函数，以及哪些组件 (这个在后面要介绍). 我还是有不同意见. 机器学习需要有洞察力 (insight), 如果基础不牢, 没有机器学习的基本思路, 就像在漆黑的屋子里面找东西一样, 纯碰运气是不气的. 本系列贴子也是希望为读建立一些 insight.

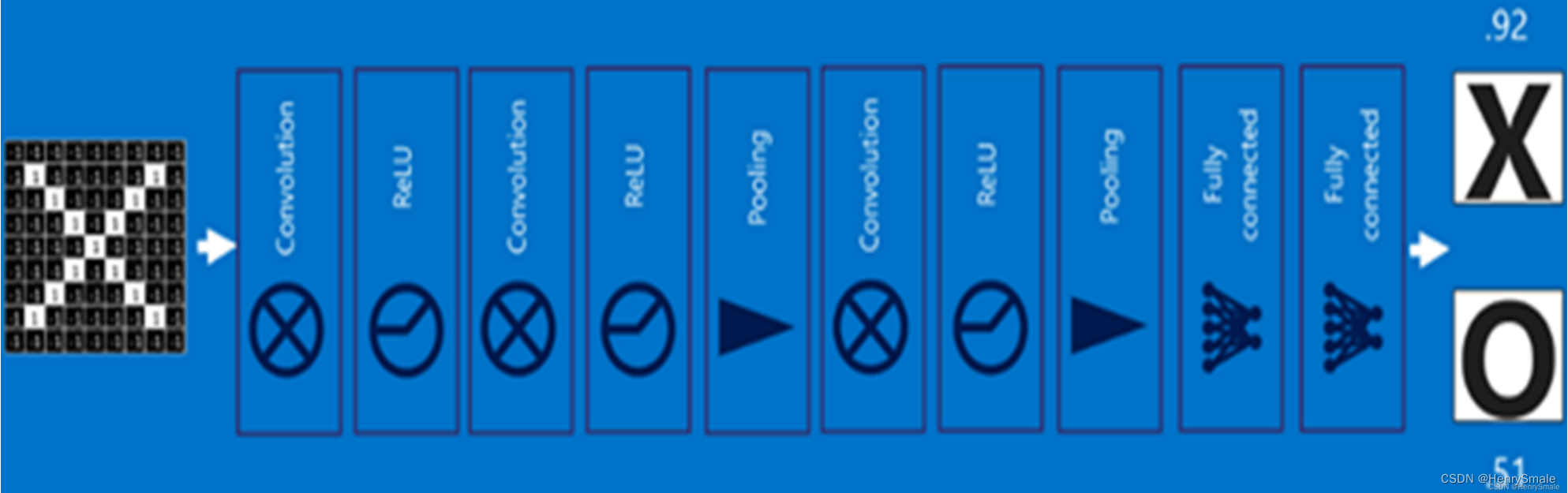
3 卷积神经网络

卷积核是个透视镜, 把原图像扫描一遍变成新图像.

3.1 卷积操作

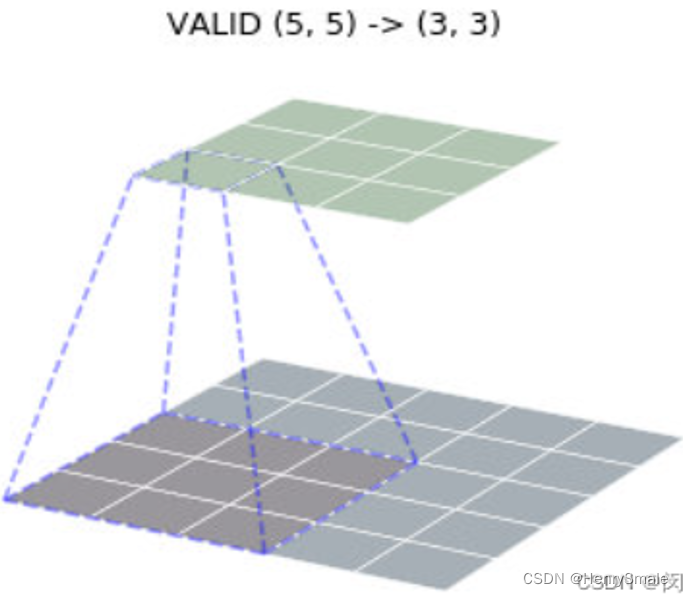
下图下平面标定的 3×3 区域, 对应于个3×3 卷积, 这 9 个数对应着相乘, 然后相加, 获得了上平面标定的 1 个小区域的值. 注意这里不是矩阵的乘法.
卷积有三种模式, 可以把图片变大 (full)、变小 (valid)、保持尺寸 (same).
与全连接网络相同, 卷积神经网络 CNN 也需要在加权和之后使用激活函数, 以使其具有非线性的优点.

卷积层：特征提取
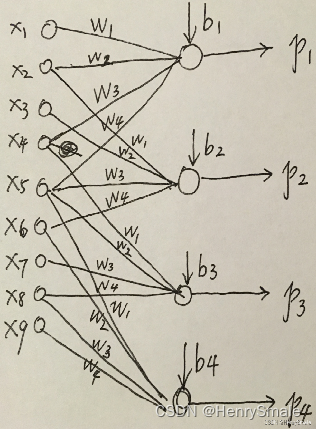
可以将图像卷积看成全连接网络的权值共享(weight sharing)

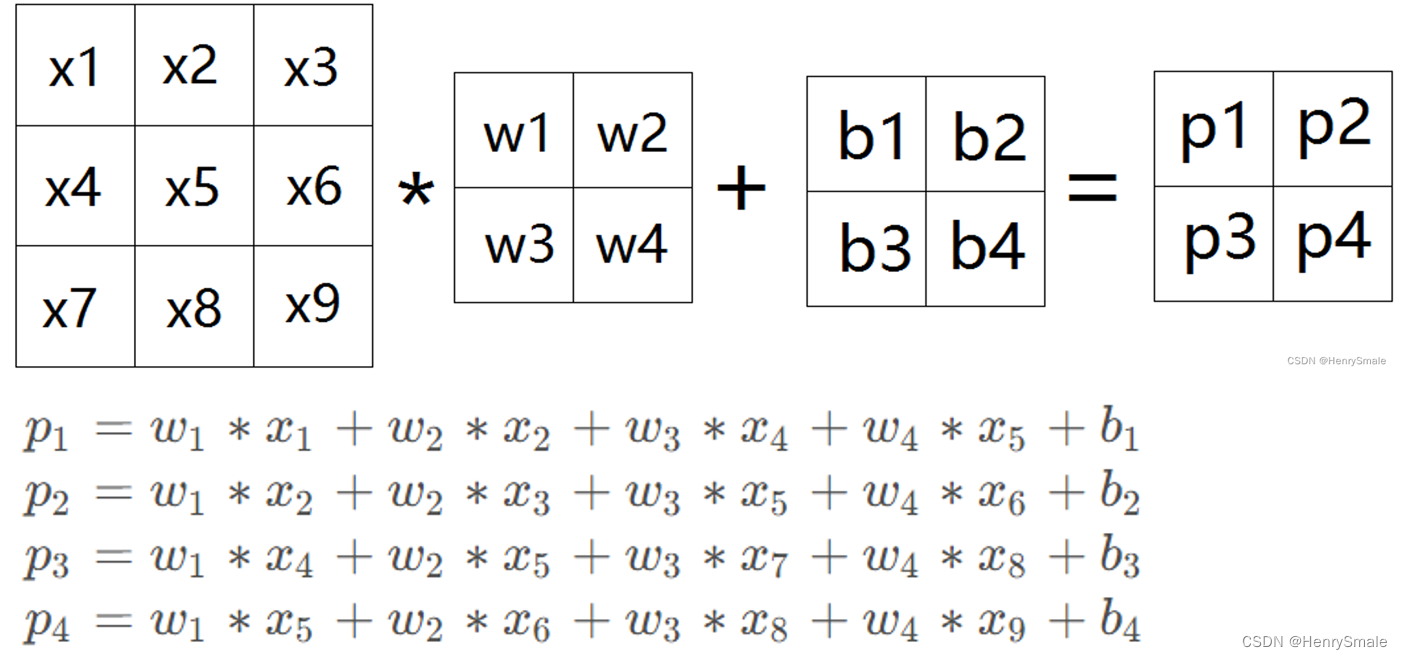
等价于下边的权值共享网络：

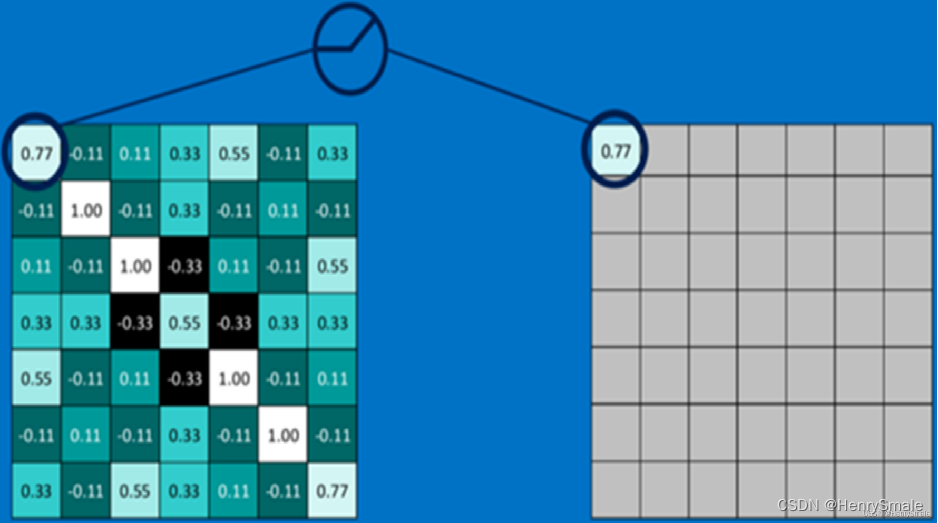
3.2 ReLU 激活层

加入非线性因素，将卷积层输出结果做非线性映射。
ReLU 函数：对于输入负值，输出全为0；正值原样输出。

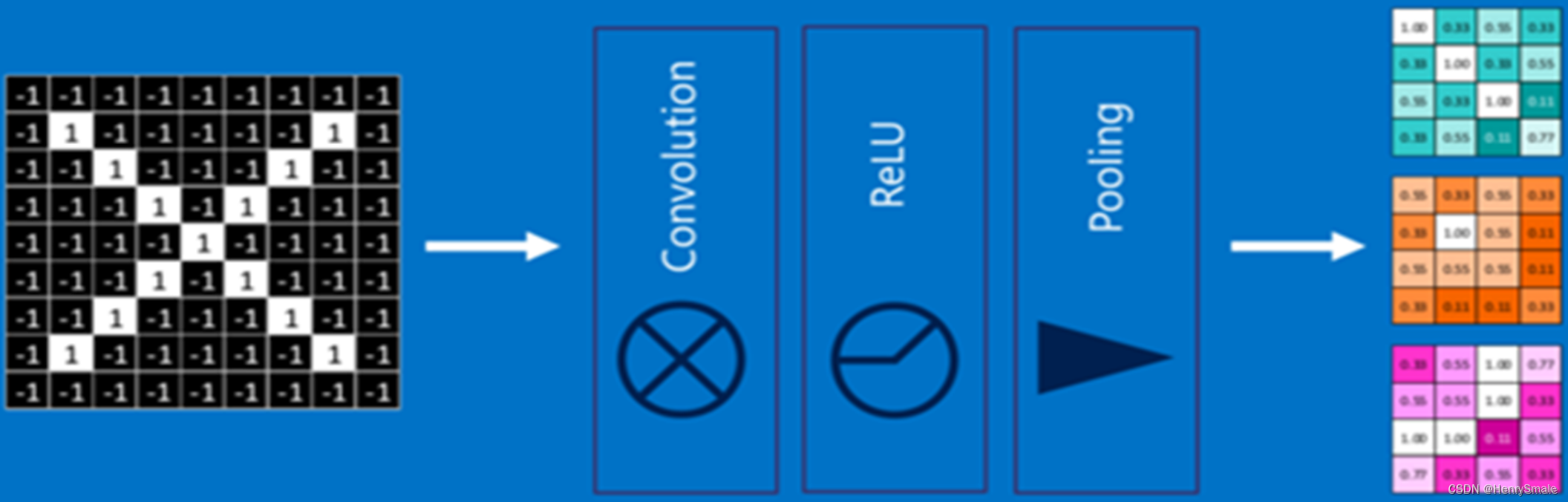
3.3 池化层：提取重要的特征信息

100×100 的图片, 用3×3 卷积核去卷, 第 2 层变成98×98 图片, 第 3 层变成96×96 图片, 太慢啦!
用池化操作可以把多个点压缩成一个点, 如把 98×98 图片每 2×2 个点取最大值 (或平均值, 最小值), 瞬间变成 49×49 的图片.
是不是很随意的样子? 有效就行.

3.4 单层卷积神经网络

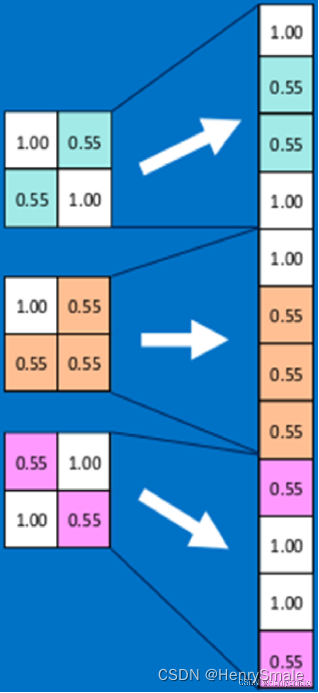
3.5 全连接层

全连接层在整个卷积神经网络中起到“分类器”的作用，即通过卷积、池化等深度网络后，再经过全连接层对结果进行识别分类.

3.6 卷积神经网络流程