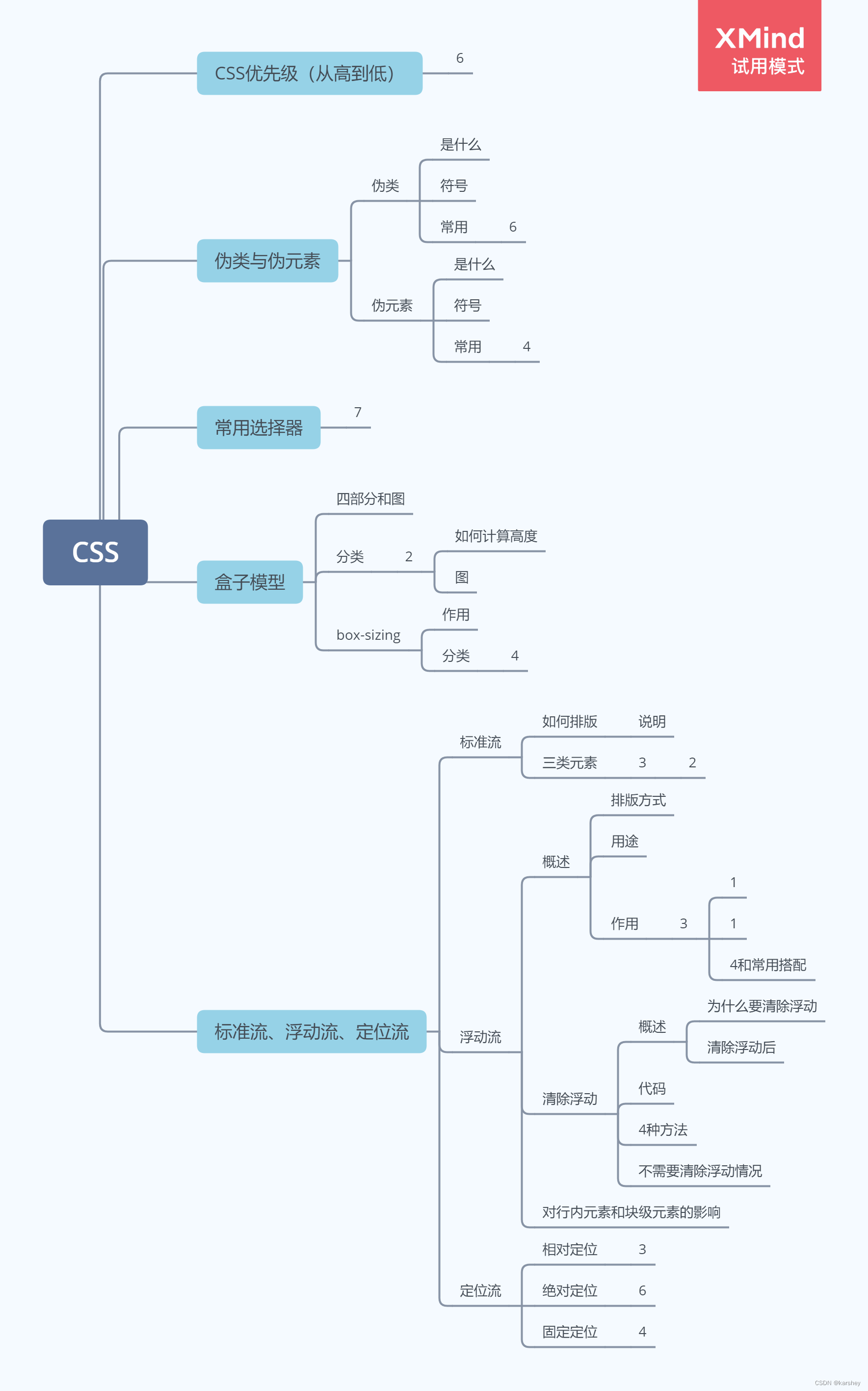
Kmp算法

解决问题：
字符串匹配问题
怎么解决？
前缀表+next[]数组
#分析
先看暴力做法：

两层for循环，一层遍历文本串，一层遍历模式串（子串）
对应的每个字符进行匹配，匹配成功就 i+ + ， j+ + 继续匹配
匹配不成功则break，退出循环.
那这样做时间复杂度为O(m*n)

再看Kmp做法
1.先将模式串和文本串一一匹配，遇到冲突，即匹配不成功时，需要退一位继续匹配。
那这一位怎么退？
借助前缀表！

2.需要求模式串的前缀表，怎么求？
先引入一个ne 数组,next数组的求算相当于双指针算法
从左至右开始遍历，计算前缀和后缀最长相等的长度
最后，得到的是一个升序序列，序列中的值便是退一位的索引，即ne[j]。

3.借助ne[]数组，进行退一位处理。
如果当前冲突了，那我们就找到模式串冲突位置j的前一位即ne[j]。
这里的话p数组做了往前移动一位处理，那这样对应的每个j冲突的退一位索引直接就是ne[j]。

4.退一位处理后，会确保ne[j]的前缀和文本串冲突位置前的串的后缀相同。
那这样就开始在 j=ne[j] 的下一位开始与冲突位置进行匹配。

如果匹配不到，则继续退一位处理，继续匹配。
如果匹配得到，则记录i的位置，注意i保留的是匹配成功的最后一位。

所以，答案下标等于 i-n+1 ，但是这里写法是从下标1开始，所以 i-n+1-1=i - n 。

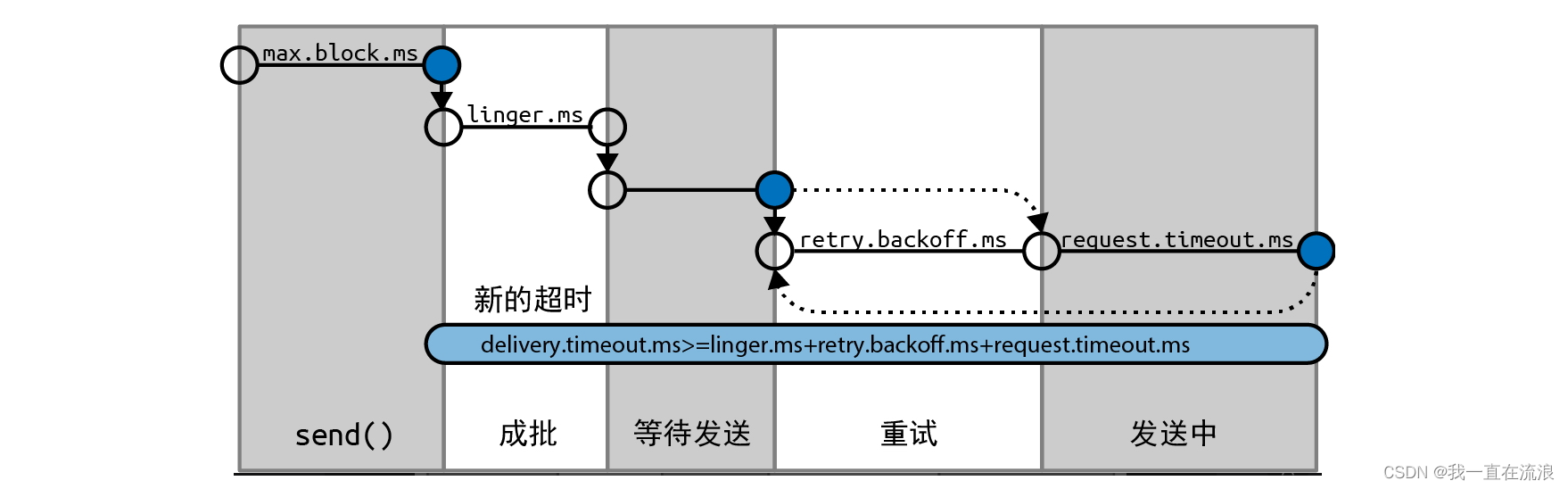
分析一下KMP算法的时间复杂度：
先for循环遍历一下，移动j的位置，最多前移m 次、后移每次，总计为2*m

所以Kmp的时间复杂度O(2*m)=O(m)

过程模拟图

分析图

在这里插入图片描述

前缀表计算展开图
注意：
前缀是不含尾字母的所有子串
后缀是不含首字母的所有子串
找到最长相等的前缀和后缀长度即可

图1

在这里插入图片描述

图二

在这里插入图片描述

图三

在这里插入图片描述

代码

import java.io.*;
public class Main{
	public static void main(String []args) throws NumberFormatException, IOException {
		BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		int N=100010,M=1000010;
		int n =  Integer.parseInt(in.readLine());
		String P = in.readLine();
		char []p = new char[N];
		//输入的数组下标从1开始
		for(int i=1;i<=n;i++) {
			p[i]=P.charAt(i-1);//将字符串P的每个字符存入字符数组
		}
		int m = Integer.parseInt(in.readLine()); 
		String S = in.readLine();
		char []s = new char[M];
		for(int i=1;i<=m;i++) {
			s[i] = S.charAt(i-1);//将字符串S的每个字符存入字符数组
		}
		
		int ne[]=new int [N];
		
		//前缀表
		//i=1时，ne[1]=0;所以从i=2开始即可。
		for(int i=2,j=0;i<=n;i++) {
		    //j从0开始，进入循环会加上1，主要是为了做退格处理。
		
			while(j>0&&p[i]!=p[j+1])j=ne[j];
			//那么我们去找他的前一位来进行匹配，即往前退一格，再比较。
			
			if(p[i]==p[j+1])j++;//匹配相等的话，则j++
			
			ne[i]=j;//更新ne数组i的值为j
		}
		
		for(int i=1,j=0;i<=m;i++) {
		    
		    //j+1是退格定位到j之后的位置再继续比较。
			while(j>0&&s[i]!=p[j+1])j=ne[j];
			
			if(s[i]==p[j+1])j++;//匹配成功，则i、j继续往下走
			
			if(j==n) {
			    //i最后记录的是字符串匹配成功的最后一位，需要i-n+1.
			    //但是这里的下标从1开始，需要减1，所以是i-n。
				
			out.write((i-n)+" ");
		
		//保存当前满足条件的ne[j]的位置，接下来继续匹配可能会用到。
				j=ne[j];
			}
		
		}
		out.flush();
		out.close();
		in.close();		
	}
}