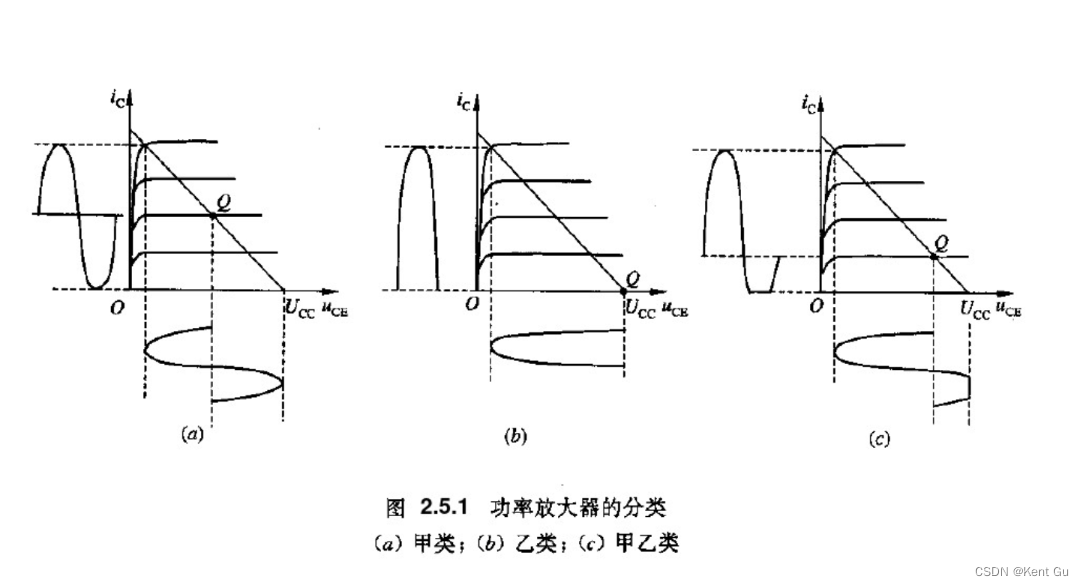
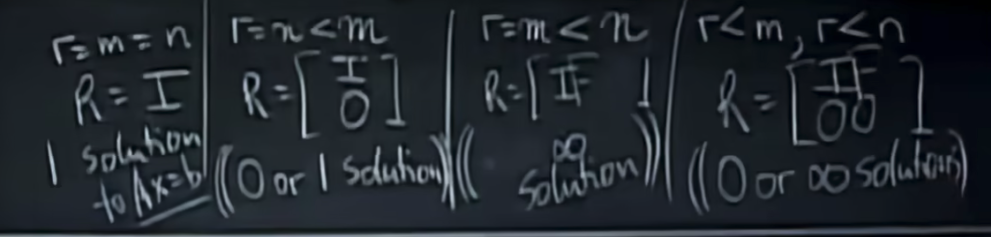这节课中主要讲解根据秩来判断方程组/矩阵的(solvability)解情况，即通过秩来判断(aumented matrix)增广矩阵的解。我们需要直接求解方程组的解就是求解矩阵的解。

x.1 判断(非齐次线性方程组)Ax=b是否有解

我们以下面这个方程组为例，它具有3个约束条件和4个自由量，

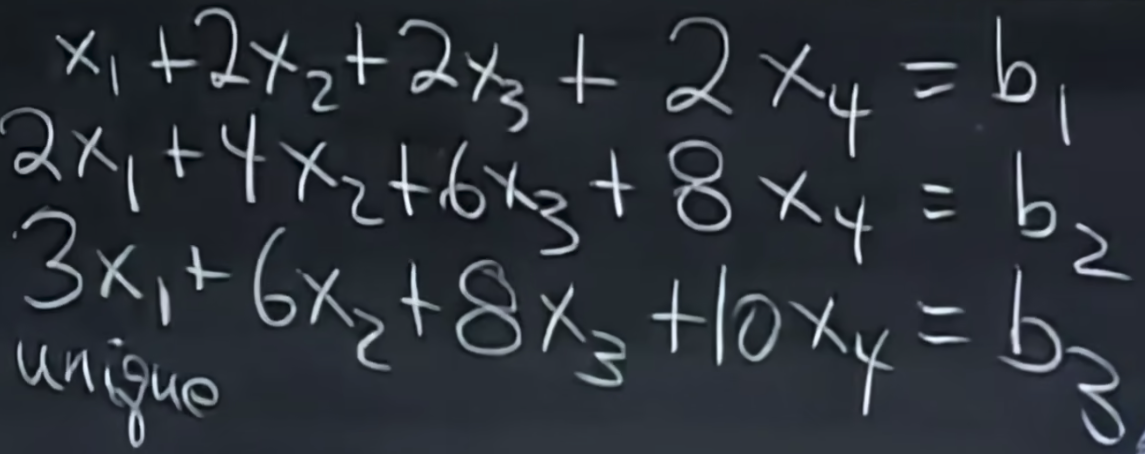
我们将其转换为矩阵的形式，不含系数[b1, b2, b3]的矩阵叫做coefficients matrix系数矩阵，包含系数的矩阵叫做(augmented matrix)增广矩阵，

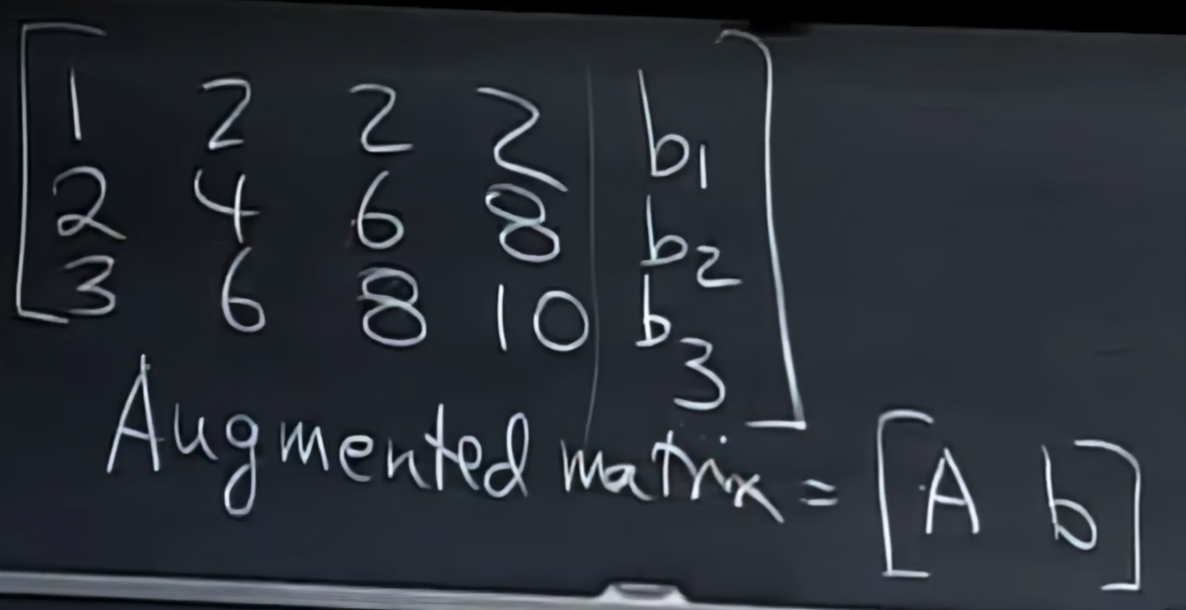
接下来我们使用(elimination)消元法对增广矩阵进行化简，得到如下的(row echelon form)阶梯矩阵，并找到了(pivot columns)主列。通过观察我们能够发现，如果该方程组要有解，则第三个方程的等号左边得等于右边，即0=b3-b2-b1，

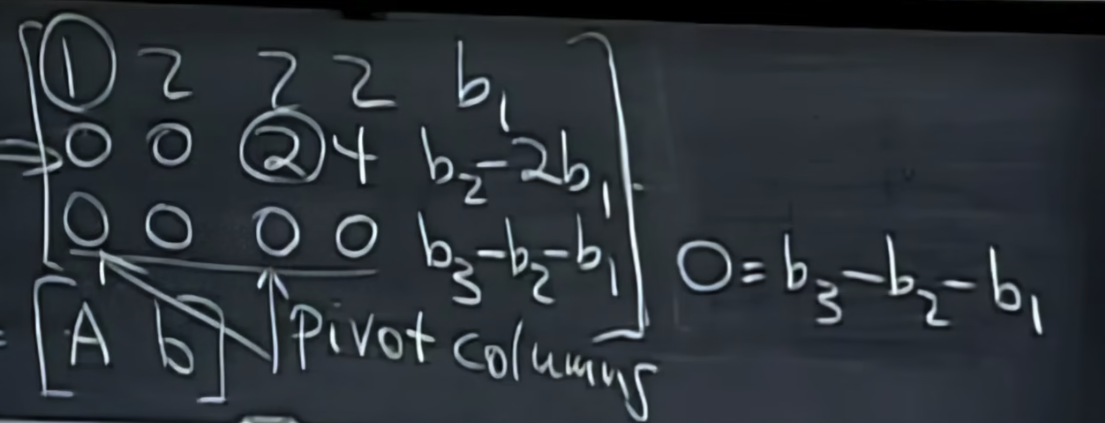
要判断形如Ax=b是否有解，我们通过线性组合的知识即判断b是否是A的列分向量的线性组合。

x.2 求解Ax=b的步骤

求解步骤分为两步走，以教程为例，先求解Ax=b的(particular solution)特解，在这一步骤中我们需要将(free variables)自由量全部设置为0，即将x2=x4=0，然后求解x1和x2，

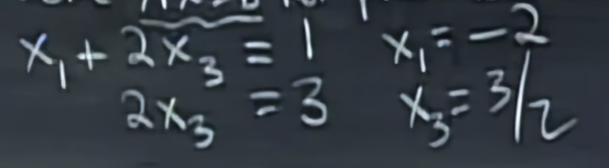
于是我们求得了特解如下，

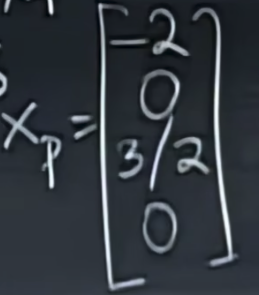
第二步，我们需要求得Ax=0的(special solution)通解，即求得(null space)零空间的通解，我们将所有的通解的线性组合和唯一的特解相加，即得到了Ax=b的所有解，推导过程如下，

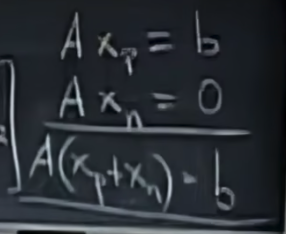
如何求解Ax=0的所有解在上一节中已经讲过。我们将特解和通解相加便得到了Ax=b的全部解，如下，

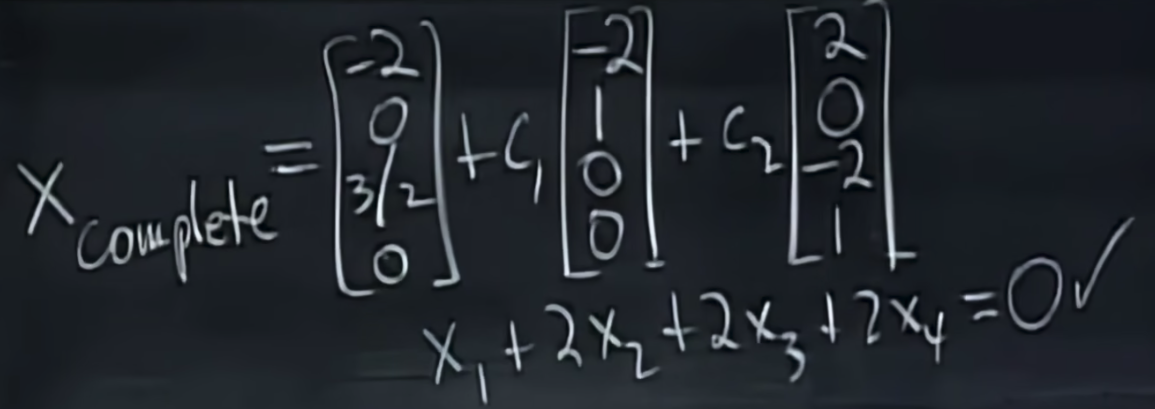
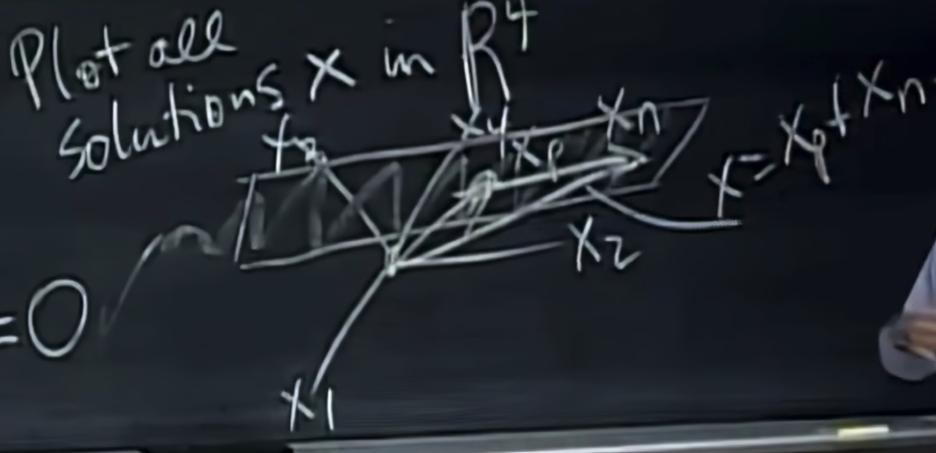
我们最终得到的解空间易见是一个四维向量空间，我们在四维空间中画出我们的解空间。易见特解是四维空间的一个点，而通解是四维空间中的平面，我们的解空间画图如下，需要注意的是他其实并不一定是我们严格定义上的(subspace)向量子空间。

x.3 通过(rank)秩来判断Ax=b的解情况

接下来是重点，对于一个形如mxn，秩为r的增广矩阵[A|b]，我们如何判断其对应的Ax=b的解情况呢？

首先我们需要知道r<=m且r<=n，而满秩矩阵则指的是r=n的矩阵，自由列的数量则是n-r。

我们总结如下，R都值得是(pref)最简矩阵，其中第三种和第四种情况中I和F相交错是因为主列和自由列不一定谁在前在后，在只做行变的前提下，他们可能是交替出现的。