论文地址：Back to MLP: A Simple Baseline for Human Motion Prediction
论文代码：https://github.com/dulucas/simlpe
论文出处：IEEE/CVF Winter Conference on Applications of Computer Vision （WACV），2023
论文单位：Grenoble INP，France

摘要

• 本文解决了人体运动预测的问题，包括从历史上观察到的序列预测未来的身体姿势。
• 然而，最先进的方法提供了良好的结果，它们依赖于任意复杂性的深度学习架构，例如RNN，Transformers或GCN，通常需要多个训练阶段和超过200万个参数。
• 在本文中，我们表明，结合一系列标准实践，如应用离散余弦变换(DCT)，预测关节的残余位移和优化速度作为辅助损失，基于多层感知器(mlp)的轻量级网络只有14万个参数可以超越最先进的性能。
• 对Human3.6M、AMASS和3DPW数据集进行了验证，显示了我们的方法（siMLPe）始终优于所有其他方法。
• 我们希望我们的简单方法可以为社区提供一个强有力的基线，并允许重新思考人体运动预测问题。

1. 简介

• 给定一个三维人体姿态序列，人体运动预测任务的目的是预测姿态序列的后续动作。
• 预测未来人体运动是许多应用的核心，包括自动驾驶中的事故预防、跟踪人或人机交互。
• 由于人体运动的时空性质，文献中常见的趋势是设计能够融合时空信息的模型。
• 传统方法主要依赖于隐马尔可夫模型或高斯过程潜变量模型。
• 然而，虽然这些方法在简单和周期性运动模式下表现良好，但在复杂运动下却明显失败。
• 近年来，随着深度学习的成功，基于不同类型的神经网络开发了各种能够处理序列数据的方法。
• 例如，一些工作使用 RNN 来建模人体运动，一些工作基于 GCN，一些工作基于Transformers，融合跨越人体关节和时间的运动序列的时空信息。
• 然而，这些新方法的体系结构通常并不简单，其中一些方法需要额外的先验，这使得它们的网络难以分析和修改。
• 因此，一个问题自然出现了:“我们可以用一个简单的网络来解决人类运动预测问题吗?”
• 为了回答这个问题，我们首先尝试了一个简单的解决方案，即重复最后一个输入姿势并将其用作输出预测。 如图1所示，这种朴素的解决方案已经可以获得合理的结果，这意味着最后一个输入姿势与未来的姿势“接近” （Repeating Last-Frame）。
  
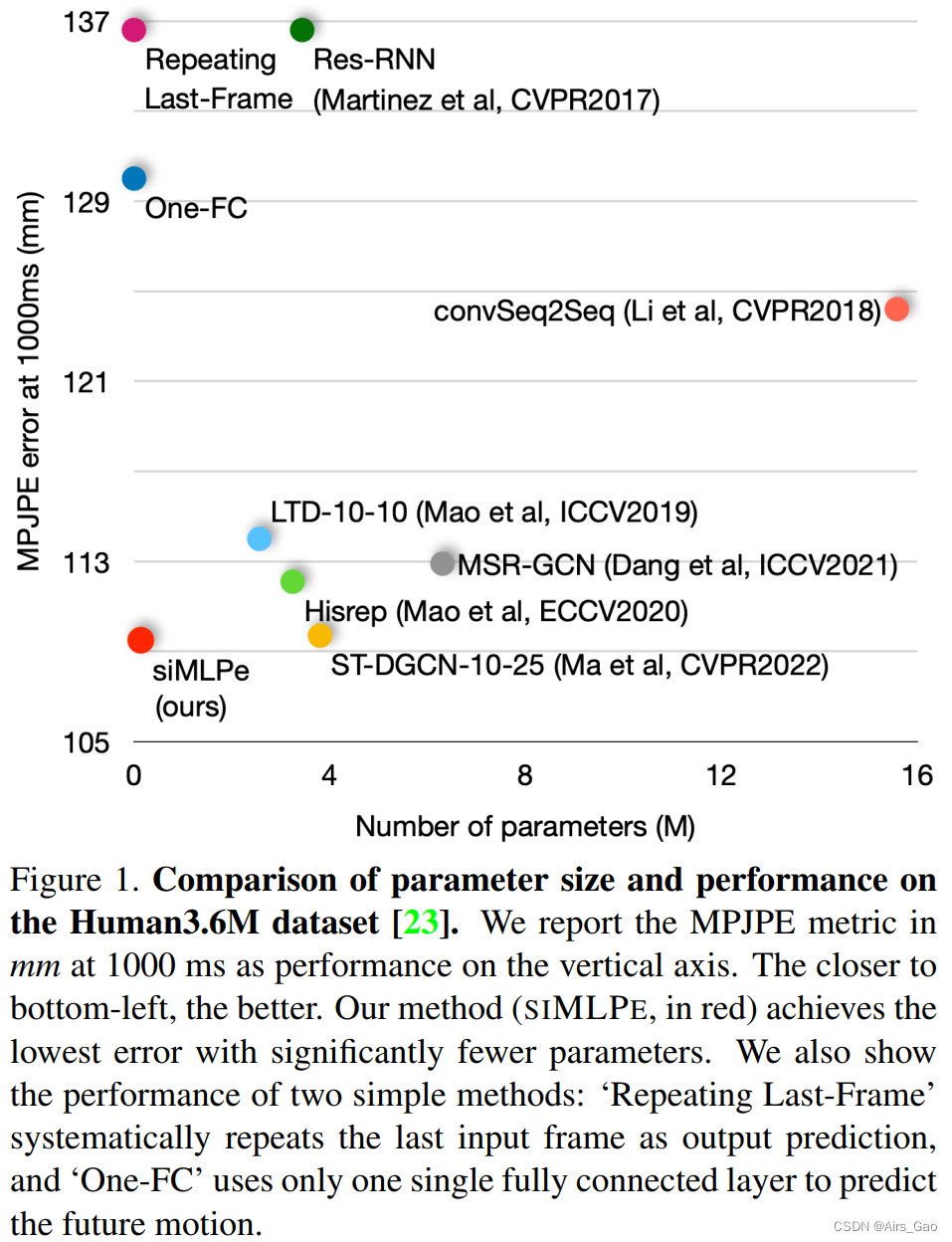
• 受此启发，我们进一步只训练一个全连接层来预测未来姿势和最后一个输入姿势之间的残差，并获得更好的性能，这显示了建立在像全连接层这样的基础层上的简单网络用于人体运动预测的潜力 （One-FC）。
• 基于上述观察，我们回到多层感知器(MLPs)，并构建一个简单而有效的网络，称为siMLPe，只有三个组成部分: fully connected layers, layer normalization, and transpose operations. 网络体系结构如图2所示。
  
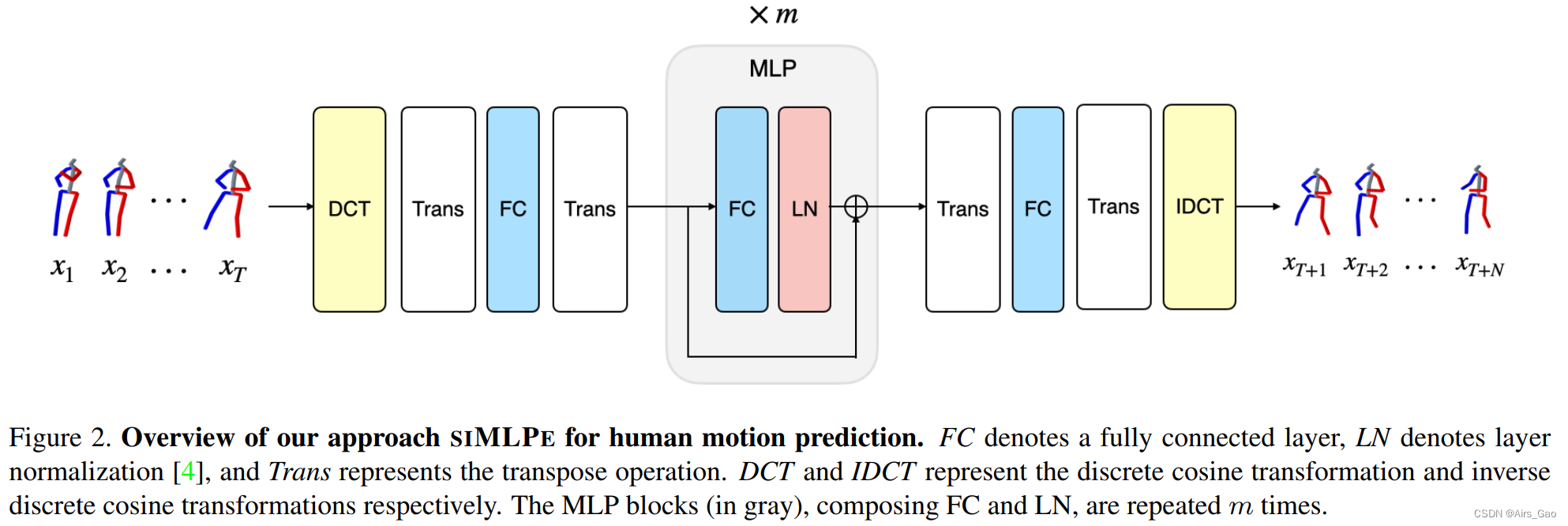
• 值得注意的是，我们发现即使是常用的激活层(如ReLU)也不需要，这使得我们的网络除了层归一化之外完全是线性模型。
• 尽管简单，但当与三个简单的做法适当结合时，siMLPe可以实现强大的性能。这三个简单的做法分别为：应用离散余弦变换(DCT)，预测关节的残余位移，优化速度作为辅助损失。
• SIMLPE在几个标准数据集上产生了SOAT性能，包括Human3.6M，AMASS，和3DPW。
• 同时，siMLPe是轻量级的，需要的参数比以前最先进的方法少20到60倍。
• SIMLPE和以前的方法的比较可以在图1显示了不同网络在Human3.6M上1000 ms时的平均每个关节位置误差(MPJPE)与网络复杂性的关系。siMLPe以高效率达到最佳性能。
• 综上所述，我们的贡献如下:
  （1）我们表明，人类运动预测可以以一种简单的方式建模，而无需明确融合空间和时间信息。作为一个极端的例子，单个全连接层已经可以达到合理的性能。
  （2）我们提出siMLPe，一个简单而有效的人体运动预测网络，只有三个组成部分: 全连接层、层归一化和转置操作，在多个基准测试(如Human3.6M，AMASS和3DPW数据集)上，以远少于现有方法的参数实现了最先进的性能。

2. Related Work

• 人体运动预测是一种序列到序列的任务，将过去观察到的运动作为预测未来运动序列的输入。
• 传统的运动预测方法都是非线性的，如马尔可夫模型、高斯过程动力学模型，和受限玻尔兹曼机。
• 这些方法已被证明可以有效地预测简单的运动，但最终难以预测复杂和长期的运动。
• 随着深度学习时代的到来，使用深度网络进行人体运动预测取得了巨大的成功，其中包括递归神经网络(Recurrent Neural networks, RNN)，图卷积网络(Graph Convolutional networks, GCNs)和Transformers，这是本节的主要重点。

2.1 基于RNN的人体运动预测

• 由于人体运动固有的顺序结构，一些工作解决了三维人体运动预测的循环模型。
• 然而，该类方法受到RNN的多重固有限制。
• 首先，RNN作为一个序列模型，在训练和推理过程中很难并行化。
• 其次，内存约束阻止RNN从更远的帧探索信息。
• 一些研究通过使用RNN变体、滑动窗口、卷积模型或对抗性训练来缓解这一问题。但是它们的网络仍然是复杂的，并且有大量的参数。

2.2 基于GCN的人体运动预测

• 为了更好地编码人体关节的空间连通性，最近的工作通常是构建人体姿态为图（graph），采用图卷积网络(graph Convolutional Networks, GCNs)进行人体运动预测。

2.3 基于 Attention 的人类运动预测

• 随着transformers的发展，一些作品试图用 Attention 机制来处理这一任务。

2.4 总结

• 综上所述，随着近年来人体运动预测的发展，基于RNN/GCN/Transformer 的结构得到了很好的探索，结果得到了显著改善。
• 虽然这些方法提供了良好的效果，但它们的架构变得越来越复杂和难以训练。
• 在本文中，我们坚持简单的架构，并提出了一个基于MLP的网络。
• 我们希望我们的简单方法可以作为一个baseline，让社区重新思考人体运动预测的问题。

3. siMLPe

• 在本节中，我们将阐述问题，并在3.1节中给出DCT变换的公式，在3.2节中给出网络架构的细节，在3.3节中给出我们用于训练的损失。
• 给定过去的3D人体姿势序列，我们的目标是预测未来的姿势序列。
• 我们将观察到的三维人体姿势表示为 x_1:T ∈ R^T×C，由 T 个连续的人体姿势组成，其中第 t 帧 x_t 处的姿势用 C 维向量表示，即：x_t∈ R^C。
• 在本工作中，与之前的工作相似，x_t 为第 t 帧节点的三维坐标，C = 3 × K，其中 K 为节点个数。
• 我们的任务是预测未来 N 个运动帧: x_T +1:T +N ∈R^N×C。

3.1 离散余弦变换（Discrete Cosine Transform (DCT)）

• 我们采用DCT变换对时间信息进行编码。
• 更精确地说，给定 T 帧的输入运动序列，DCT矩阵 D∈R^T×T可以计算为：
  
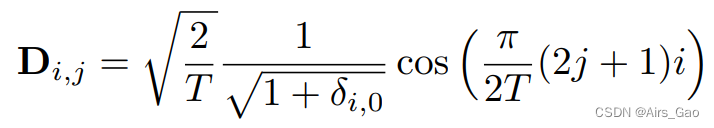
  其中δ_i,j表示Kronecker函数, δ_i,j 为：
  
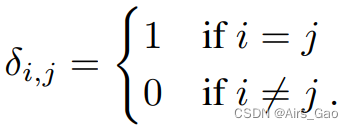
• 离散余弦变换后的输入是：D(x_1:T) = Dx_1:T。
• 我们应用**反向离散余弦变换(IDCT)**将网络的输出转换回原始姿态表示，表示为D^-1和D的逆。

3.2 网络架构

• 图2显示了我们网络的体系结构。我们的网络只包含三个组成部分: 全连接层、转置操作、层归一化。
• 对于所有的全连通层，它们的输入维数等于输出维数。
• 形式上，给定一个三维人体姿势的输入序列 x_1:T ∈R^T×C，我们的网络预测一个未来的姿势序列x_T+1:T+N ∈ R^N×C:
  
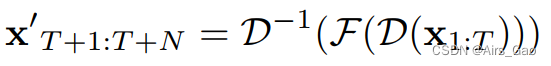
  F 表示我们的网络。
• DCT变换后，我们应用一个全连接层，只对变换后的运动序列 D(x_1:T)∈R^T×C的空间维度进行操作：
  
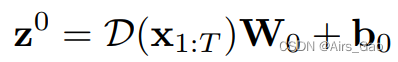
  其中z⁰∈R^T×C为全连通层的输出。W⁰∈R^C×C, b⁰∈R^C表示全连通层的可学习参数。
• 在实践中，这相当于对一个全连接层应用转置操作，然后将输出特征转置回去，如图2所示。
• 然后，引入一系列 m 块，仅在时间维度上操作，即仅跨帧合并信息。
• 每个块由一个全连接层组成，然后进行层规范化，表示为：
  
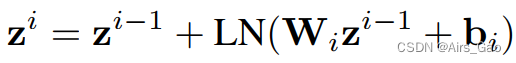
  式中，zⁱ∈R^T×C, i∈[1,…, m] 表示第 i 个MLP块的输出。
  LN表示层归一化操作。
  Wⁱ∈R^T×T和 bⁱ∈R^T是第 i 个MLP块中全连通层的可学习参数。
• 最后，与第一个全连接层类似，我们在MLP块之后再添加一个全连接层，只对特征的空间维度进行操作，然后应用IDCT变换得到预测结果：
  
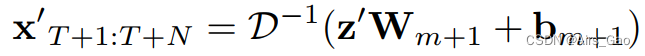
  其中W_m+1和 b_m+1是最后一个全连接层的可学习参数。
• 注意长度 T 和 N 不需要相等。当T > N时，我们只取预测的N个前帧，在T < N的情况下，我们可以通过重复最后一帧将输入序列填充到N。

3.3 Losses

• 正如第1节中提到的，如图1所示，最后一个输入姿势与未来的姿势 “接近”。
• 通过这种观察，我们让网络预测未来姿态 x_T+t 和最后输入姿态 x_T 之间的残差，而不是从头开始预测绝对3D姿态。 这简化了学习并提高了性能。

目标函数

• 我们的目标函数 L 包括两项 Lre 和 Lv：
  
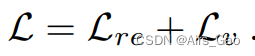
• Lre的目标是最小化预测运动 x_T+1:T+N 和真实运动x_T+1:T+N 之间的 L2 范数：
  
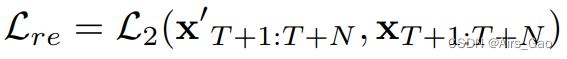
• Lv 的目的是最小化预测运动速度 v_T+1:T+N 与地面真实速度 vT+1:T+N之间的 L2 范数:
  
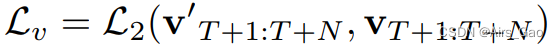
  式中 v_T+1:T+N ∈R^N×C, v_T表示第 t 帧的速度，用时间差计算: v_T = x_t+1−x_t。

4. 实验

4.1 数据集

• Human3.6M：
  Human3.6M包含7个演员表演15个动作，每个姿势标记32个关节。
  我们遵循测试协议，使用S5作为测试集，S11作为验证集，其他作为训练集。
  以前的工作使用了不同的测试采样策略，包括每个动作8个样本，每个动作256个样本或测试集中的所有样本。
  由于8个样本太少，取所有的测试样本无法平衡不同序列长度的不同动作，因此我们每个动作取256个样本进行测试，并在22个关节上进行评估。
• AMASS：
  AMASS是多个动作捕捉数据集的集合，使用统一的SMPL参数化。
  我们使用AMASS- bmlrub作为测试集，并将AMASS数据集的其余部分分成训练集和验证集。
  模型在18个关节上进行了验证。
• 3DPW：
  3DPW是一个包含室内和室外场景的数据集。
  一个姿势由26个关节表示，我们使用在AMASS上训练的模型评估18个关节来评估泛化。

4.2 评价指标

• 本文使用三维关节坐标上的平均关节位置误差(Mean Per Joint Position Error，MPJPE)作为评价指标。这是评估3D姿态误差最广泛使用的指标。
• 该度量计算预测和真实之间不同节点的平均L2 -范数。
• 与之前的工作相似，我们忽略了姿态的全局旋转和平移，保持采样率为 25 FPS 的所有数据集。