C++ 不知算法系列之聊聊希尔、归并排序算法中的分治哲学

news2024/11/27 14:49:57

1. 前言

排序算法中，冒泡、插入、选择属于相类似的排序算法，这类算法的共同点：通过不停地比较，再使用交换逻辑重新确定数据的位置。

希尔、归并、快速排序算法也可归为同一类，它们的共同点都是建立在分治思想之上。把大问题分拆成小问题，解决所有小问题后，再合并每一个小问题的结果，最终得到对原始问题的解答。

Tips： 通俗而言：化整为零，各个击破。

分治算法很有哲学蕴味：老祖宗所言 合久必分，分久必合，分开地目的是为了更好的合并。

分治算法的求解流程：

  • 分解问题：将一个需要解决的、看起很复杂 原始问题 分拆成很多独立的**子问题**，子问题与原始问题有相似性。

  • 求解子问题：子问题除了与原始问题具有相似性，也具有独立性，即所有子问题都可以独立求解。

  • 合并子问题： 合并每一个子问题的求解结果最终可以得到原始问题的解。

下面通过深入了解希尔排序算法，看看分治算法是如何以哲学之美的方式工作的。

2. 希尔排序

讲解希尔之前，先要回顾一下插入排序。插入排序的平均时间复杂度，理论上而言和冒泡排序是一样的 O（n2），但如果数列是前部分有序，则每一轮只需比较一次，对于 n 个数字的原始数列而言，时间复杂度可以达到 O(n)。

插入排序的时间复杂度为什么会出现如此有意思的变化？

  • 插入排序算法的排序思想是尽可能减少数字之间的交换次数。
  • 通常情形下，交换处理的时间大约是移动的 3 倍。这便是插入排序的性能有可能要优于冒泡排序的原因。

希尔排序算法本质就是插入排序，或说是对插入排序的改良。

希尔算法的理念：让原始数列不断趋近于排序，从而降低插入排序的时间复杂度。当数列局部有序时，全局必然是趋向于有序。

希尔排序的实现流程：

  • 把原始数列从逻辑上切割成诸多个子数列。
  • 对每一个子数列使用插入排序算法排序。
  • 当所有子数列完成后，再对原数列进行最后一次插入算法排序。

希尔排序的关键在于如何切分子数列，切分方式可以有 2 种：

2.1 前后切分

如有原始数列=[3，9，8，1，6，5，7] ，采用前后分可分成如下图所示的 2 个子数列。

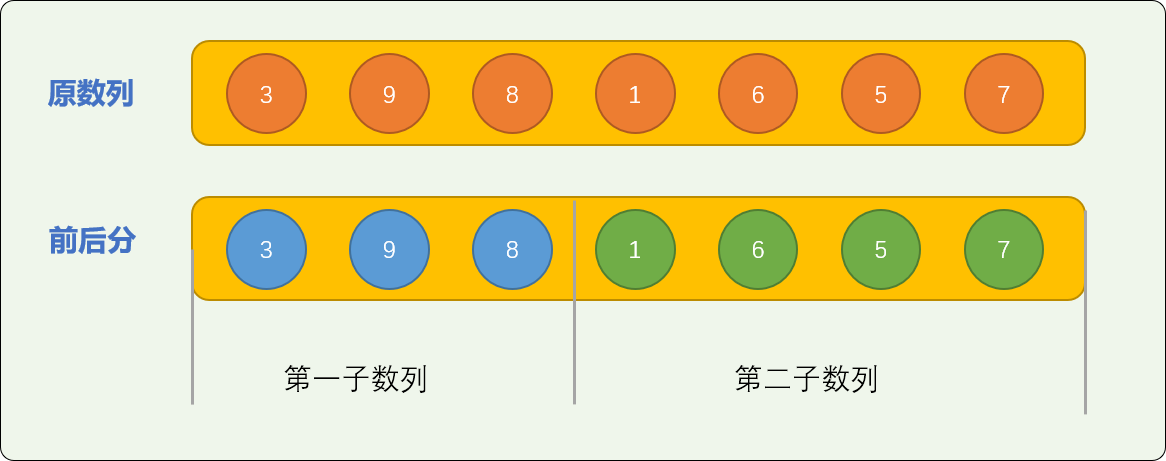
s01.png

然后对前、后部分的数列使用插入算法排序。

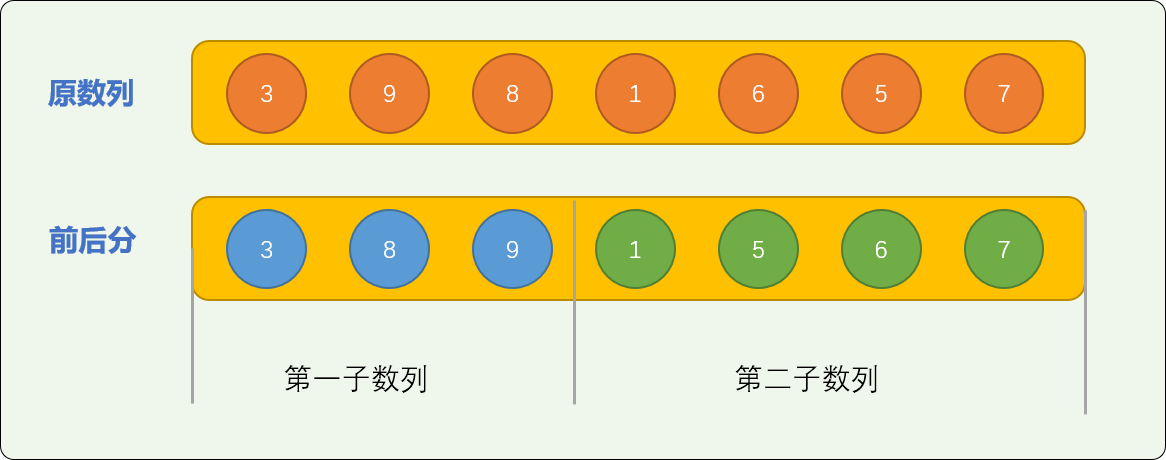
s02.png

如上图所示，子数列排序后，要实现原始数列的最终有序，则后部分的数字差不多全部要以超车的方式，插入到前部分数字的中间，交换量较大。

理想的状态是数字整体有序，需要交换的次数不多。所以前后分这种一根筋的切分方式，对于原始问题的最终性能优化起不了太多影响。

2.2 增量切分

增量切分采用间隔切分方案，可能让数字局部有序以正态分布。

增量切分，需要先设定一个增量值。如对原始数列=[3，9，8，1，6，5，7] 设置切分增量为 3 时，整个数列会被切分成 3 个逻辑子数列。增量数也决定最后能切分多少个子数列。

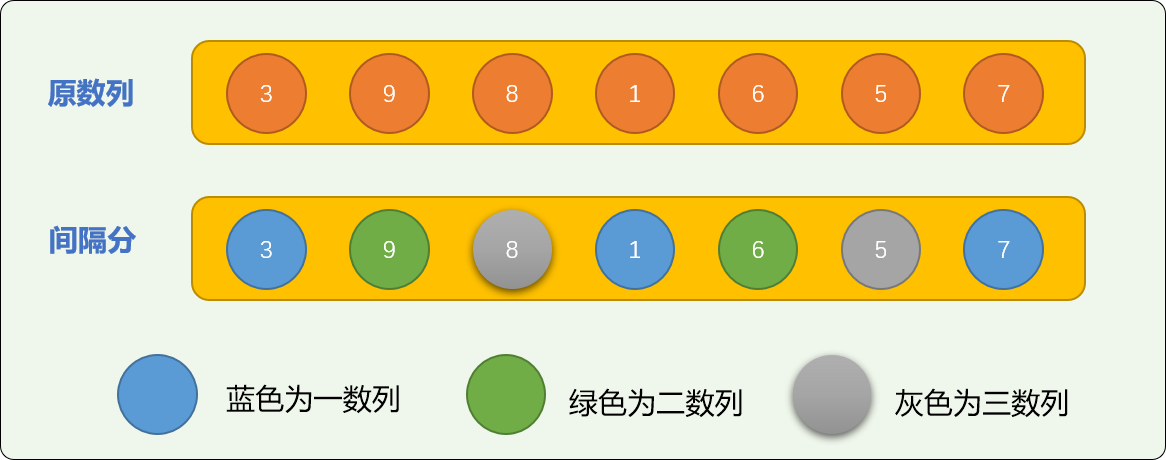
s03.png

对切分后的 3 个子数列排序后可得到下图。

s04.png

下面两张图是增量切分前后数字位置的变化图，可以看出来，几乎所有的数字都产生了位置变化 ，且位置变化的跨度较大。如数字 9 原始位置是 1，经过增量切分再排序后位置可以到 4，已经很接近 9 的最终位置 6 了。有整体趋于有序的势头，在此基础之上，再进行插入排序的的次数要少很多。

s16.png

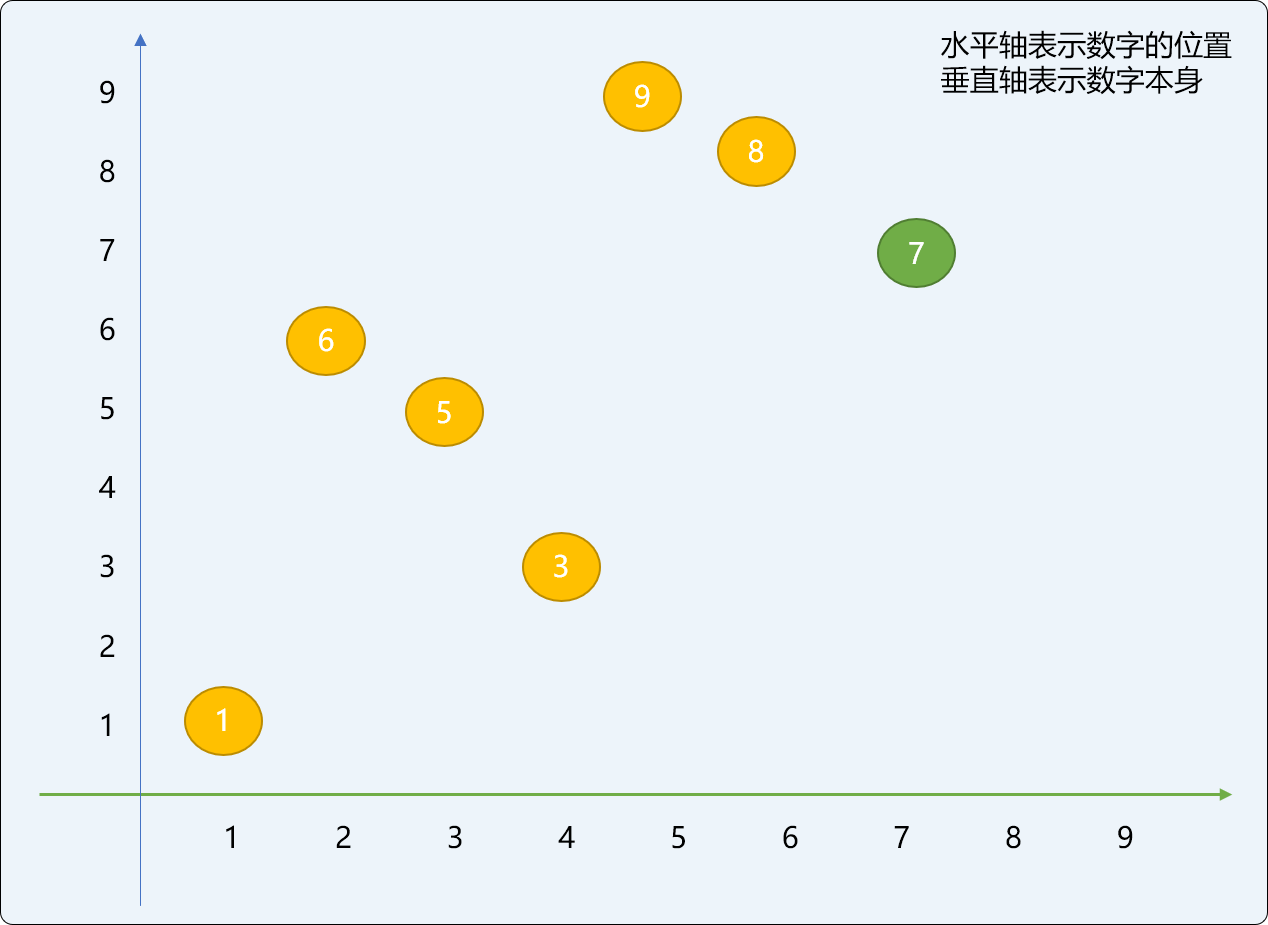
s18.png

实现希尔排序算法时，最佳的方案是先初始化一个增量值，切分排序后再减少增量值，如此反复直到增量值等于 1 （也就是对原数列整体做插入排序）。

Tips： 增量值大，数字位置变化的跨度就大，增量值小，数字位置的变化会收紧。

编码实现希尔排序：

#include <iostream>
using namespace std;
// 插入排序
void insertSort(int nums[],int size, int start,int increment) {
//后指针指向原数列的第 2 个数字,所以索引号从 1 开始
for(int backIdx=start + increment; backIdx<size; backIdx+=increment) {
	// 初始，前指针和后指针的关系，
	int frontIdx = backIdx;
	while(frontIdx>=0 && nums[frontIdx]<nums[frontIdx-increment] ) {
		//交换
		int tmp=nums[frontIdx];
		nums[frontIdx]=nums[frontIdx-increment];
		nums[frontIdx-increment]=tmp;
		}
	}
}
// 希尔排序
void shellSort(int nums[],int size) {
	// 增量
	int increment=size/2;
	// 新数列
	while (increment > 0) {
		// 增量值是多少，则切分的子数列就有多少
		for(int start=0; start<increment; start++) {
			insertSort(nums,size, start, increment);  
		}
		// 修改增量值，直到增量值为 1
		increment = increment / 2;
	}
}
int main(int argc, char** argv) {
	int nums[] = {3, 9, 8, 1, 6, 5, 7};
	int size=sizeof(nums)/4;
	shellSort(nums,size);
	for(int i=0; i<size; i++ ) {
		cout<<nums[i]<<"\t";
	}
	return 0;
}

这里会有一个让人疑惑的观点：难道一次插入排序的时间复杂度会高于多次插入排序时间复杂度？

通过切分方案，经过子数列的微排序（因子数列数字不多，其移动交换量也不会很大），最后一次插入排序只需要在几个数字之间微调，甚至不需要。只要增量选择合适，时间复杂度可以控制 在 O(n) 到 O（n2）之间。完全是有可能优于单纯的使用一次插入排序。

3. 归并排序

归并排序算法也是基于分治思想。和希尔排序一样，需要对原始数列进行切分，但是切分的方案不一样。

相比较希尔排序，归并排序的分解子问题，求解子问题，合并子问题的过程分界线非常清晰。可以说，归并排序更能完美诠释什么是分治思想。

3.1 分解子问题

归并排序算法的分解过程采用二分方案。

  • 把原始数列一分为二。

  • 然后在已经切分后的子数列上又进行二分。

  • 如此反复，直到子数列不能再分为止。

    如下图所示：

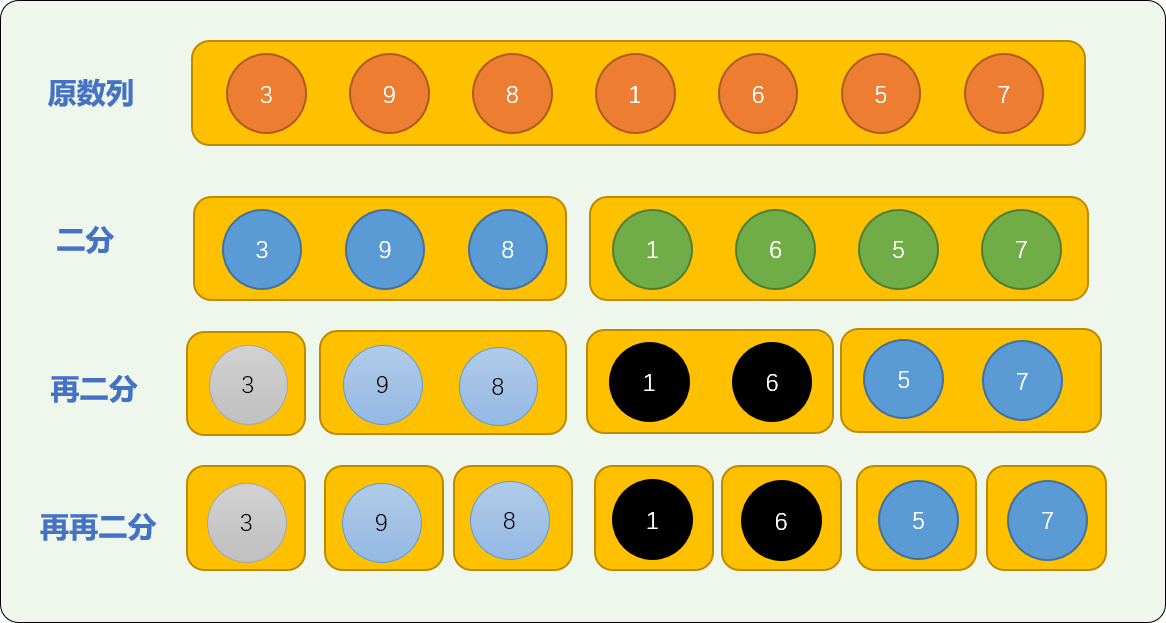
s05.png

如下代码，使用递归算法对原数列进行切分，通过输出结果观察切分过程：

#include <iostream>
using namespace std;
// 切分原数列
void splitNums(int nums[],int start,int end ) {
	int size=end-start;
	for(int i=start; i<size+start; i++)
		cout<<nums[i]<<"\t";
	cout<<endl;
	if (size>1)  {
		// 切分线，中间位置
		int spLine = size / 2;
		splitNums(nums,start,spLine+start);
		splitNums(nums,spLine+start,end );
	}
}
int main(int argc, char** argv) {
	int  nums[] = {3, 9, 8, 1, 6, 5, 7};
	int size=sizeof(nums)/4;
	splitNums(nums,0,size);
	return 0;
}

输出结果： 和上面演示图的结论一样。

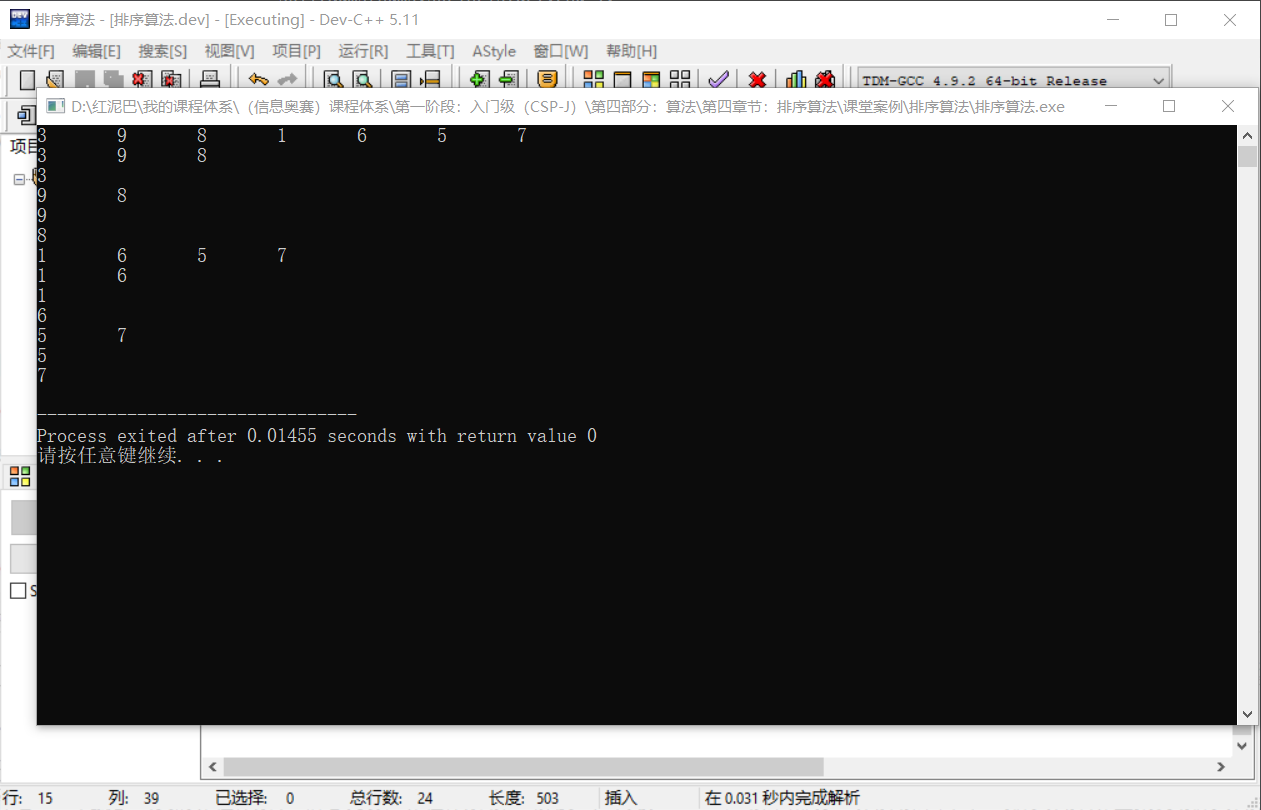
s19.png

3.2 求解子问题

因为已经切分到了原子性，可认为子数列是有序的。然后对相邻2 个子数列进行合并，合并后要保证数字依然有序。

如何实现 2 个有序子数列合并后依然有序？

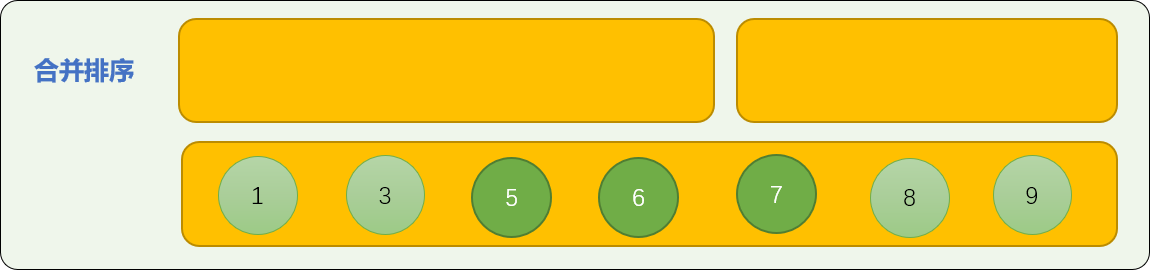
使用首数字比较算法进行合并排序。如下图演示了如何合并 nums01=[1,3,8,9]、nums02=[5,6,7] 2 个子数列。

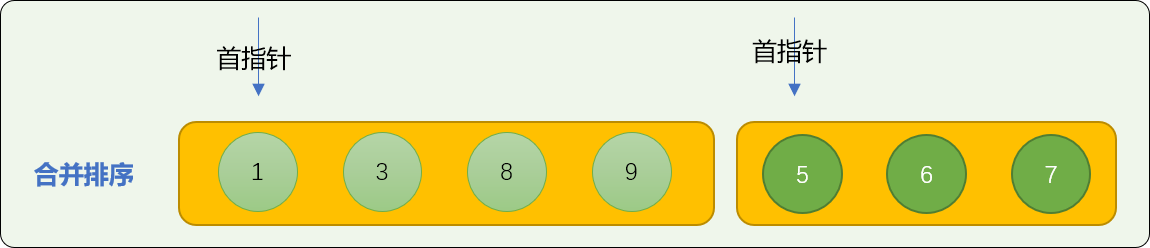
s07.png

  • 数字 1 和 数字 5 比较，5 大于 1 ，数字 1 先位于合并数列中。

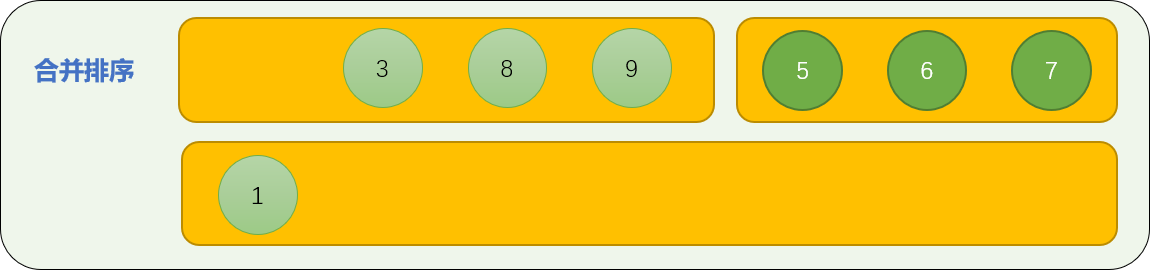
s08.png

  • 数字 3 与数字 5 比较，数字 3 先进入合并数列中。

s09.png

  • 数字 8 和数字 5 比较，数字 5 进入合并数列中。

s10.png

  • 重复上述过程，比较首数字的大小。最后，可以保证合并后的数列是有序的。

s11.png

3.3 归并子问题

前面是分步讲解切分和合并逻辑，现在把切分和合并逻辑合二为一，完成归并算法的实现。

#include <iostream>
using namespace std;
int  nums_[] = {3, 9, 8, 1, 6, 5, 7};
// 切分原数列
void splitNums(int nums[],int start,int end ) {
	int size=end-start;
	if (size>1)  {
		// 切分线，中间位置
		int spLine = size / 2;
		//前子数组的绝对大小
		int s1=spLine;
		//后子数组的绝对大小
		int s2=end-spLine-start;
		//前面的子数组
		int nums01[s1];
		int idx=0;
		//切分原数组,注意相对位置
		for(int i=start; i<spLine+start; i++) {
			nums01[idx]=nums_[i];
			idx++;
		}
		int nums02[s2];
		idx=0;
		for(int i=spLine+start; i<end; i++) {
			nums02[idx]=nums_[i];
			idx++;
		}
		splitNums(nums01,start,spLine+start);
		splitNums(nums02,spLine+start,end );
		// 为 2 个数列创建 2 个指针
		int idx_01 = 0;
		int  idx_02 = 0;
		int k = 0;
		while (idx_01 < s1 and idx_02 < s2 ) {
			if (nums01[idx_01] > nums02[idx_02]) {
				// 合并后的数字要保存到原数列中
				nums[k] = nums02[idx_02];
				idx_02 += 1;
			} else {
				nums[k] = nums01[idx_01];
				idx_01 += 1;
			}
			k += 1;
		}
		// 检查是否全部合并
		while (idx_02 < s2) {
			nums[k] = nums02[idx_02];
			idx_02 += 1;
			k += 1	;
		}
		while (idx_01 < s1) {
			nums[k] = nums01[idx_01];
			idx_01 += 1;
			k += 1;
		}
	}
}
int main(int argc, char** argv) {
	int size=sizeof(nums_)/4;
	splitNums(nums_,0,size);
	cout<<"归交排序："<<endl;
	for(int i=0;i<size;i++ ){
		cout<<nums_[i]<<"\t";
	}
	return 0;
}

输出结果：

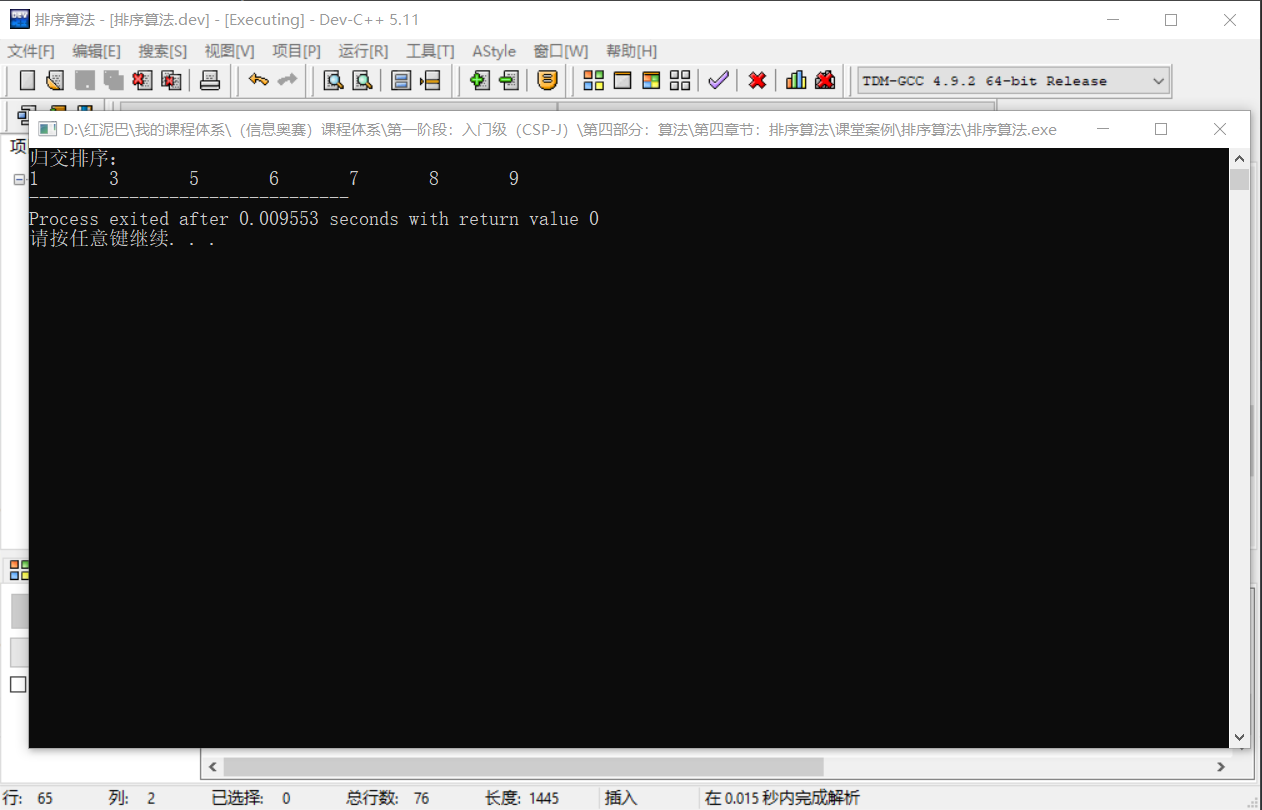
s20.png

从归并算法上可以完整的看到分治理念的哲学之美。

4. 基数排序

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或 bin sort。

Tips： 基数排序没有使用分治理念，放在本文一起讲解，是因为基数排序有一个对数字自身切分逻辑。

基数排序的最基本思想：

如对原始数列 nums = [3, 9, 8, 1, 6, 5, 7] 中的数字使用基数排序。

  • 先提供一个长度为 10 的新空数列（本文也称为排序数列）。

    Tips： 为什么新空数列的长度要设置为 10？等排序完毕，相信大家就能找到答案。

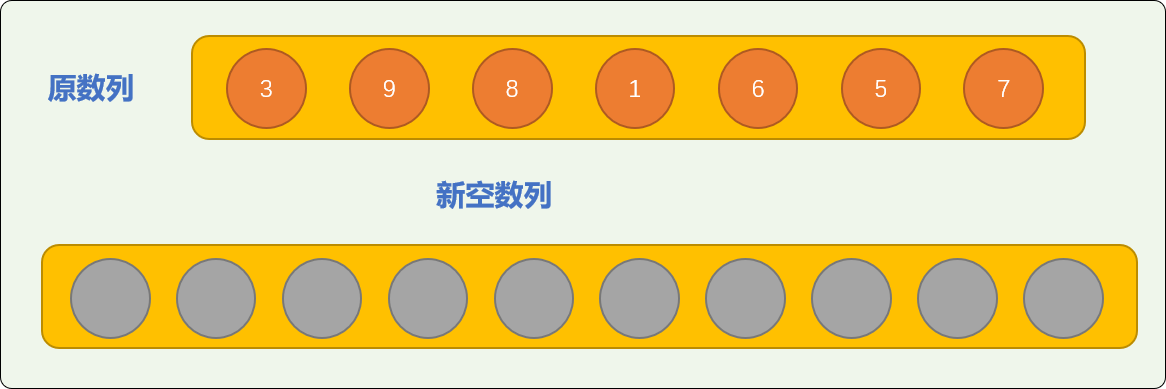
s12.png

。把原数列中的数字转存到新空数列中，转存方案：

​ nums 中的数字 3 存储在新数列索引号为 3 的位置。

​ nums 中的数字 9 存储在新数列索引号为 9 的位置。

​ nums 中的数字 8 存储在新数列索引号为 8 的位置。

​ ……

s13.png

从上图可知，原数列中的数字所转存到排序数列中的位置，是数字所代表的索引号所指的位置。显然，经过转存后，新数列就是一个排好序的数列。

编码实现：

#include <iostream>
using namespace std;
int main(int argc, char** argv) {
	// 原数列
	int nums[] = {3, 9, 8, 1, 6, 5, 7};
	int size=sizeof(nums)/4;
	// 找到数列中的最大值
	int maxVal=nums[0];
	for(int i=1; i<size; i++) {
		if( nums[i]>maxVal )
			maxVal=nums[i];
	}
	int sortNums[maxVal+1]= {0};
	for (int i : nums) {
		sortNums[i]=i;
	}
	for (int i : sortNums) {
		if(i!=0)
			cout<<i<<"\t";
	}
	return 0;
}

上述排序的缺点：

  • 新空数列的长度定义为多大由原始数列中数字的最大值来决定。如果数字之间的间隔较大时，新数列的空间浪费就非常大。

如对 nums=[1,98,51,2,32,4,99,13,45] 使用上述方案排序，新空数列的长度要达到 99 ，真正需要保存的数字只有 7 个，如此空间浪费几乎是令人恐怖的。

所以，有必要使用改良方案。如果在需要排序的数字中出现了 2 位以上的数字，则使用如下法则：

  • 先根据每一个数字个位上的数字进行存储。个位数是 1 存储在位置为 1 的位置，是 9 就存储在位置是 9 的位置。如下图：

s14.png
可看到有可能在同一个位置保存多个数字。这也是基数排序也称为桶子法的原因。

Tips： 一个位置就是一个桶，可以存放多个具有相同性质的数字。如上图：个位上数字相同的数字就在一个桶中。

  • 把存放在排序数列中的数字按顺序重新拿出来，这时的数列顺序变成 nums=[1，51，2，32，13，4，45，8，99]
  • 把重组后数列中的数字按十位上的数字重新存入排序数列。

s15.png

可以看到，经过 2 轮转存后，原数列就已经排好序。

Tips： 这个道理是很好理解的：现实生活中，我们在比较 2 个数字 大小时，可以先从个位上的数字相比较，然后再对十位上的数字比较。如此，无论是多少位的数字，都可以运用基数排序算法。

基数排序，很有生活的味道！！

编码实现基数排序： 下面代码使用递归实现。

#include <iostream>
#include <cmath>
using namespace std;
//排序用数组
int sortNums[10][10]= {0};
void baseSort(int nums[],int size,int start,int depth) {
	if(start==depth) {
		return;
	}
	//取位
	for(int i=0; i<size; i++) {
		int wei=pow(10,start);
		int temp=nums[i] / wei %  10;
		for(int j=0; j<10; j++) {
			if( sortNums[temp][j]==0 ) {
				sortNums[temp][j]=nums[i] ;
				break;
			}
		}
	}
	//取出排序的数据
	int idx=0;
	for(int row=0; row<10; row++) {
		for(int col=0; col<10; col++) {
			if( sortNums[row][col]!=0 ) {
				nums[idx]=sortNums[row][col];
				sortNums[row][col]=0;
				idx++;
			}
		}
	}
	//递归
	baseSort(nums,size,start+1,depth);
}
int main(int argc, char** argv) {
	// 原数列
	int nums[] = {1, 98, 51, 2, 32, 114, 99, 13, 45};
	int size=sizeof(nums)/4;
	int bakNums[size];
	for(int i=0; i<size; i++) {
		bakNums[i]=nums[i];
	}
	//找到最大值
	int maxVal=nums[0];
	for(int i=1; i<size; i++) {
		if(nums[i]>maxVal) {
			maxVal=nums[i];
		}
	}
	//计算最大值的位数
	string str= to_string(maxVal);
	int depth=str.size();
	//基数排序
	baseSort(nums,size,0,depth);
	for(int i=0; i<size; i++) {
		cout<<nums[i]<<"\t";
	}
	return 0;
}

输出结果：

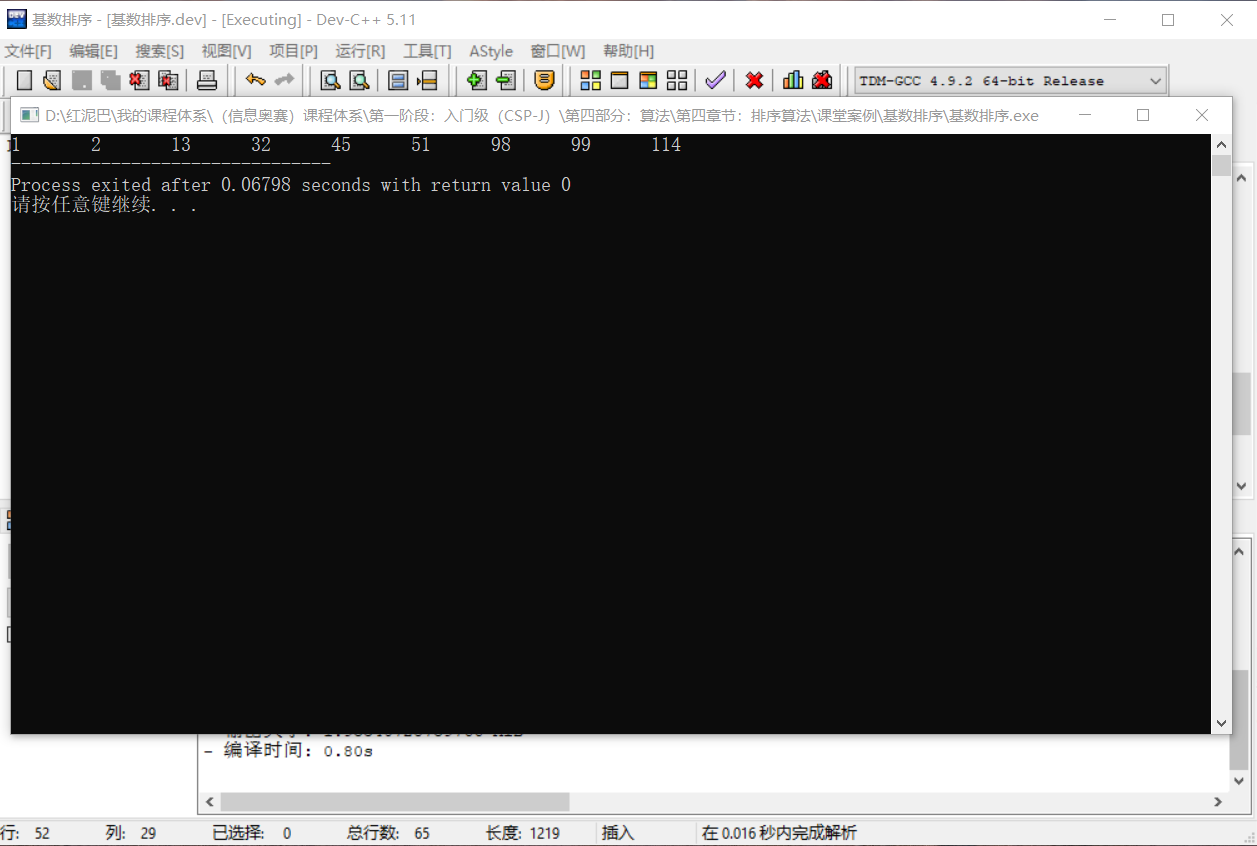
s21.png

上述转存过程是由低位到高位，也称为 LSD ，也可以先高位后低位方案转存MSD。

5. 总结

分治很有哲学味道，当你遇到困难，应该试着找到问题的薄弱点，然后一点点地突破。

当遇到困难时，老师们总会这么劝解我们。分治其实和项目开发中的组件设计思想也具有同工异曲之处。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/85839.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux基本工具——gcc/g++与make/Makefile

Linux基本工具——gcc/g++与make/Makefile

Linux编译器&#xff0c;项目构成工具gcc/g程序翻译过程选项的含义动态链接静态链接如何识别静态链接和动态链接Linux项目自动化构建工具——make/Makefilemake/Makefile是什么make/Makefile的使用伪目标make/makefile推导过程gcc/g 程序翻译过程 预处理&#xff08;去掉注释…
阅读更多...
当了10年程序员，我开窍了

当了10年程序员，我开窍了

有人说&#xff0c;程序员的高收入和工作年限成正比&#xff0c;认为自己的薪资应该如此计算&#xff1a; private static boolean 计算工资() { //years工作时长(年) int years 5; while(years-- > 0){ 做项目(); 团建活动(); 涨工资(); 拿年终奖(); } return 跳槽() &…
阅读更多...
12、后渗透测试--meterpreter使用

12、后渗透测试--meterpreter使用

Post后渗透模块&#xff1a;在meterpreter > 中我们可以使用以下的命令来实现对目标的操作。一、基本系统命令 sessions # sessions –h 查看帮助sessions -i <ID值> # 进入会话 -k 杀死会话background # 将当前会话放置后台info # 查看已有模块信息getuid …
阅读更多...
CSS之段落样式

CSS之段落样式

1、文本缩进 标签&#xff1a;text-indent &#xff08;indent v. 缩进&#xff09;含义&#xff1a;首行缩进和字体大小有关&#xff1a;1个em等于一个字体大小 2、文本对齐方式 标签&#xff1a;text-align (align v. 调整&#xff0c;使一致)种类&#xff1a;左对齐、右对…
阅读更多...
AFDet: Anchor Free One Stage 3D Object Detection

AFDet: Anchor Free One Stage 3D Object Detection

论文链接&#xff1a;https://arxiv.org/pdf/2006.12671v1.pdf 前言 在嵌入式系统上操作的高效点云3D目标检测对于包括自动驾驶在内的许多机器人应用来说都是重要的。 大多数以前的工作都试图使用基于Anchor的检测方法来解决这个问题&#xff0c;这些方法有2个缺点&#xff1…
阅读更多...
《MySQL的基础语法》

《MySQL的基础语法》

【一】现实当前的数据库 show databases:记住这里的databases是复数形式&#xff0c;你可以简单理解为它不仅仅含有一个数据库&#xff0c;所以需要用到可数名词复数形式。 【二】创建数据库 create database 数据库的名字&#xff1a;记住这里的database用的是单数形式&#…
阅读更多...
Django demo项目搭建

Django demo项目搭建

安装 Django 在应用程序开发中&#xff0c;分别创建env文件夹和wordspace文件夹。 env文件夹用于存放创建的虚拟环境&#xff0c;wordspace用于存放项目代码&#xff0c;至此实现虚拟环境和应用程序代码的分隔。 步骤1&#xff1a;创建文件夹&#xff0c;创建命令为mkdir en…
阅读更多...
静态链接：空间与地址分配

静态链接：空间与地址分配

前言 我们终于走到了链接这一步&#xff0c;对于链接这一步&#xff0c;它是将多个输入目标文件链接后输出一个可执行文件。我们拿两个程序a.c和b.c来举例说明链接的过程。 a.c&#xff1a; /* a.c */ extern int shared;int main(){int a 100;swap(&a,&shared); }…
阅读更多...
从Mybatis到Mybatis-Plus学习

从Mybatis到Mybatis-Plus学习

从Mybatis到Mybatis-PlusMybatis的入门Mybatis的配置解析核心配置文件分页配置注解开发mybatis的执行流程多对一一对多动态SQLmybatis 的缓存Mybatis-plus快速入门mybatis-plus的框架结构图分页查询和删除执行SQL分析打印条件构造器Wrapper代码生成器Mybatis的入门 环境&#…
阅读更多...
io复用函数的使用

io复用函数的使用

目录 一、概念 二、使用 1.select系统调用 代码实现 前言&#xff1a; 一般多客户端在和服务器通信时&#xff0c;服务器在执行recv时会先阻塞&#xff0c;然后按照顺序依次处理客户端&#xff0c;无论客户端有无数据都会被处理&#xff0c;这样大大降低了执行效率。此时就引…
阅读更多...
代理 模式

代理 模式

代理模式 Proxy Pattern 为其他对象提供一个代理以控制对这个对象的访问 可以详细控制访问某个&#xff08;某类&#xff09;对象的方法&#xff0c;在调用这个方法前做前置处理&#xff0c;调用这个方法后做后置处理。 静态代理 直接写死的代码的代理逻辑 动态代理 动态…
阅读更多...
12.2、后渗透测试--令牌窃取

12.2、后渗透测试--令牌窃取

攻击机kali&#xff1a;192.168.11.106靶机windows server 2008 R2&#xff1a;192.168.11.134&#xff08;包含ms17_010漏洞&#xff09;一、令牌简介与原理 令牌(Token) 就是系统的临时密钥&#xff0c;相当于账户名和密码&#xff0c;用来决定是否允许这次请求和判断这次请求…
阅读更多...
二进制搭建k8s——部署node节点

二进制搭建k8s——部署node节点

上篇&#xff1a;二进制搭建k8s——部署etcd集群和单master 二进制搭建k8s——部署node节点二进制搭建k8s——部署node节点环境部署node节点部署网络组件方法一&#xff1a;部署Flannel方法二&#xff1a;部署 CalicoCNI网络插件介绍Kubernetes的三种网络K8S 中 Pod 网络通信&a…
阅读更多...
浅浅讲解下Linux内存管理之CMA

浅浅讲解下Linux内存管理之CMA

说明&#xff1a; Kernel版本&#xff1a;4.14ARM64处理器&#xff0c;Contex-A53&#xff0c;双核使用工具&#xff1a;Source Insight 3.5&#xff0c; Visio 1. 概述 Contiguous Memory Allocator, CMA&#xff0c;连续内存分配器&#xff0c;用于分配连续的大块内存。CMA…
阅读更多...
c语言内存和文件处理有关知识

c语言内存和文件处理有关知识

内存 分配内存的函数calloc&#xff0c;malloc 定义于头文件 <stdlib.h>功能malloc分配内存(函数)calloc分配并清零内存(函数)realloc扩充之前分配的内存块(函数)free归还还之前分配的内存(函数)aligned_alloc(C11)分配对齐的内存(函数) 函数原型 void *malloc(unsigne…
阅读更多...
Java基础之Collection的ArrayList

Java基础之Collection的ArrayList

Java基础之Collection的ArrayList一、add()与addAll()二、remove()三、trimToSize()1、案例一、add()与addAll() 跟C 的vector不同&#xff0c;ArrayList没有push_back()方法&#xff0c;对应的方法是add(E e)&#xff0c;ArrayList也没有insert()方法&#xff0c;对应的方法是…
阅读更多...
Oracle---初学篇

Oracle---初学篇

Oracle初学篇 Oracle的启动&#xff0c;监听&#xff0c;用户 文章目录Oracle初学篇Oracle的启动Oracle的监听监听服务的主要文件1.listener.ora2.tnsnames.ora3.sqlnet.oraOracle用户Oracle安装成功后默认的三个用户创建用户Oracle的启动 之前写了关于如何在CentOS7上搭建Ora…
阅读更多...
2021年全国研究生数学建模竞赛华为杯D题抗乳腺癌候选药物的优化建模求解全过程文档及程序

2021年全国研究生数学建模竞赛华为杯D题抗乳腺癌候选药物的优化建模求解全过程文档及程序

2021年全国研究生数学建模竞赛华为杯 D题 抗乳腺癌候选药物的优化建模 原题再现&#xff1a; 一、背景介绍   乳腺癌是目前世界上最常见&#xff0c;致死率较高的癌症之一。乳腺癌的发展与雌激素受体密切相关&#xff0c;有研究发现&#xff0c;雌激素受体α亚型&#xff0…
阅读更多...
LeetCode 0547. 省份数量：图的连通分量

LeetCode 0547. 省份数量：图的连通分量

【LetMeFly】547.省份数量 力扣题目链接&#xff1a;https://leetcode.cn/problems/number-of-provinces/ 有 n 个城市&#xff0c;其中一些彼此相连&#xff0c;另一些没有相连。如果城市 a 与城市 b 直接相连&#xff0c;且城市 b 与城市 c 直接相连&#xff0c;那么城市 a …
阅读更多...
Windows文件夹开启大小写敏感

Windows文件夹开启大小写敏感

Windows 的文件系统的文件名&#xff0c;是大小写不敏感的&#xff0c;也就是你的文件名是 a.txt 或者 A.txt&#xff0c;在 Windows 中都是一视同仁&#xff0c;认为是同一个文件。 自从 Windows 10 引入 Linux 子系统&#xff08;WSL&#xff09;后&#xff0c;有越来越多开…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023