前言

本篇主要介绍AVL树的插入功能。其中就包含了最重要的旋转。

通过旋转来使得树平衡，是学习AVL树的一个重点，也是也是一个难点。

正式开始

先简单介绍一下AVL树。

AVL树在二叉搜索树的基础上添加了一项规定，就是保证每个结点的左右子树高度之差的绝对值不超过1，如果能够实现的话，那么就能生成一棵接近满二叉树的二叉搜索树。这样就能使得搜索的效率直线上升，这样生成出来的树就是AVL树，也叫高度平衡二叉搜索树。

如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。

那么：如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在$O(lo{g}_{2}n)$，搜索时间复杂度O($lo{g}_{2}n$)

写代码之前先看图：

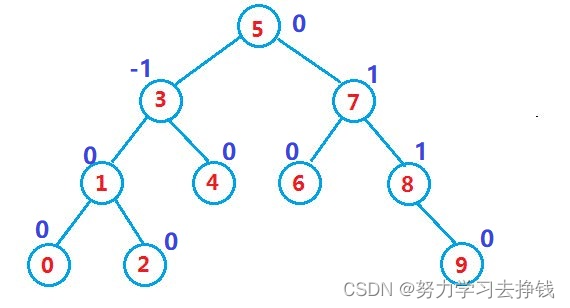
注释：

1. 每个节点跟前蓝色标记为 平衡因子 (balance factor)，用来记录当前节点的做右子树高度差。代码实现时，我会以 bf 来表示某个节点的平衡因子。

当左树和右树高度相同时，记为0。
当左树比右树高一个节点时，记为-1。
当右树比左树高一个节点时，记为1。

bf 的取值只有上述三种情况，没有其他。因为要按照AVL标准去实现，左右子树高度差的绝对值不超过1。

2. 因为插入一个节点，只会影响其祖宗节点的 bf，所以当插入一个节点后，要不断更新其祖先节点的 bf，因此我们可以在树节点中添加一个指向父节点的指针来方便我们更新祖先节点的 bf。

祖先节点是指从当前节点到树的根节点的所有节点，包含自身，比如说上图中2的祖先节点就是2,1,3,5

3. 更新祖先节点 bf 的规律如下：

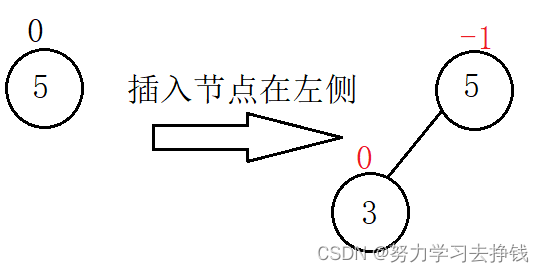
当新增节点在某节点的左侧时，该节点的 bf 减一。
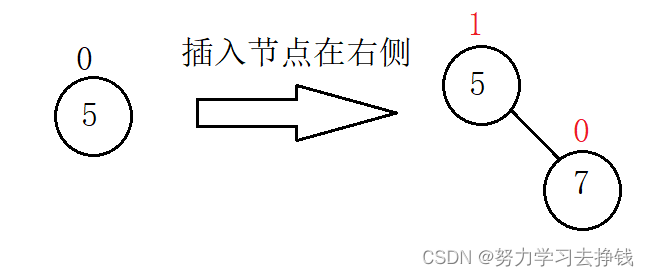
当新增节点在某节点的右侧时，该节点的 bf 加一。
如图：

插入节点后，父节点 bf 变为-1 或 1，说明原来为0，即左右子树高度相同，插入后有一边变高，parent高度变了，需要继续往上更新。
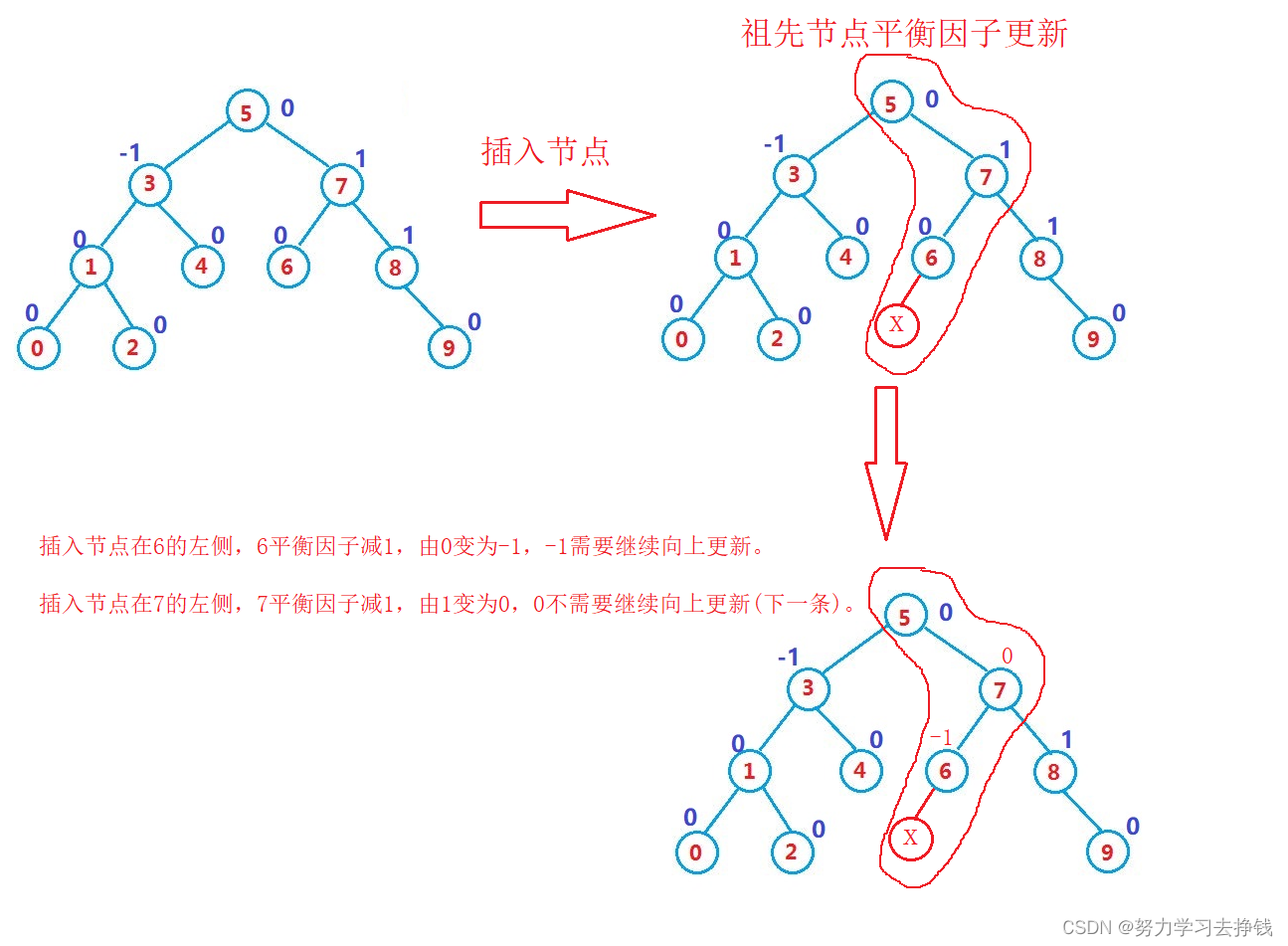
如图：

插入节点后，父节点 bf 变为0，说明原来为 -1 或者 1，即左右子树一高一低，插入后两边一样高，插入填上了矮的那一棵子树，所以parent所在的子树高度不变，其父节点的平衡因子就不需要更新，所以不需要继续往上更新了。
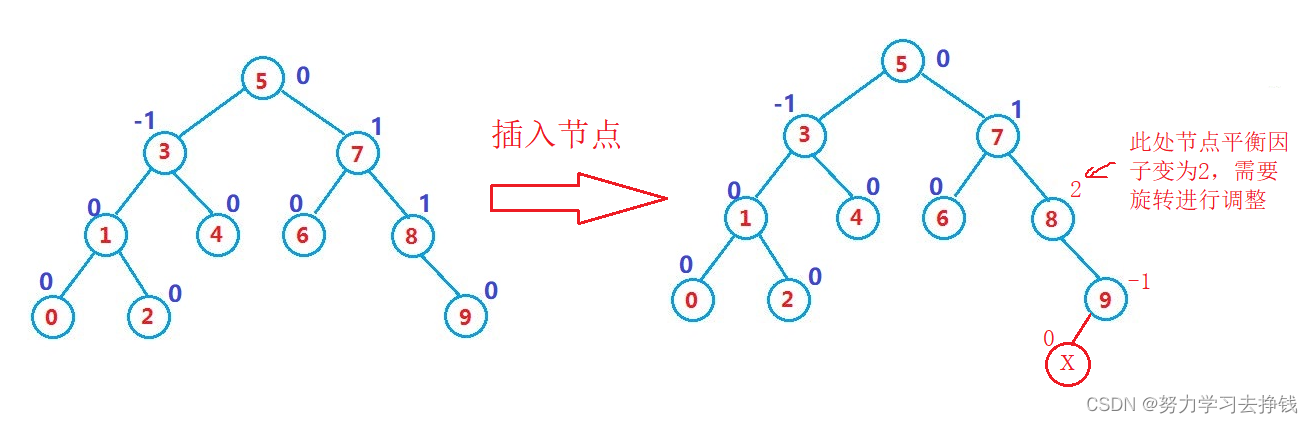
如上图中节点7，插入节点在其左侧，其平衡因子减一变为0，说明做右子树此时高度相同，不需要再继续向上更新了。

插入节点后，父节点 bf 变为 2 或 -2 ，说明原来为 -1 或者 1，即已经达到平衡的临界值了，插入后变为 2 或 -2，打破了平衡，所以parent所在子树需要旋转处理。
如图：

插入节点后，父节点 bf > 2 或 < -2 ，这是不可能出现的情况，若出现说明插入前就不是AVL树，需先检查之前操作的问题。

旋转等会再细讲，相信各位看了半天了理论已经有些腻了，下面来点代码：

树节点

本篇是以key/value模型来实现的。

节点存放内容如下：

构造函数：

树

初始情况下，就一个节点就够了：

然后来写insert，其实插入的时候就是按照二叉搜索树那样插入的，只是遇到了某节点平衡因子变为2时，就要对该节点进行旋转就好。

insert

先来写出二叉搜索树的插入：

上面我故意把旋转的情况留了下来，那么下面我们就来细说旋转。

旋转

旋转分为四种，左单旋，右单旋，左右双旋，右左双旋。

分别对应四种特殊情况。其实就两个，单旋会一个另一个单旋就会了，双旋也是。都很相似。

先说简单点的单旋。

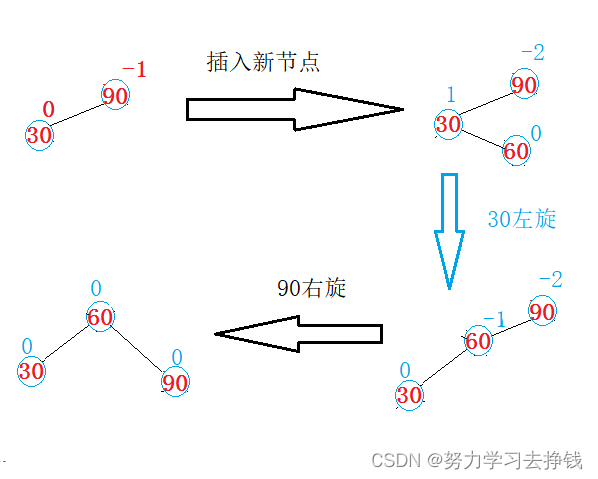
左单旋

当插入节点在较高右子树的右侧。即右右。

对应的抽象图：

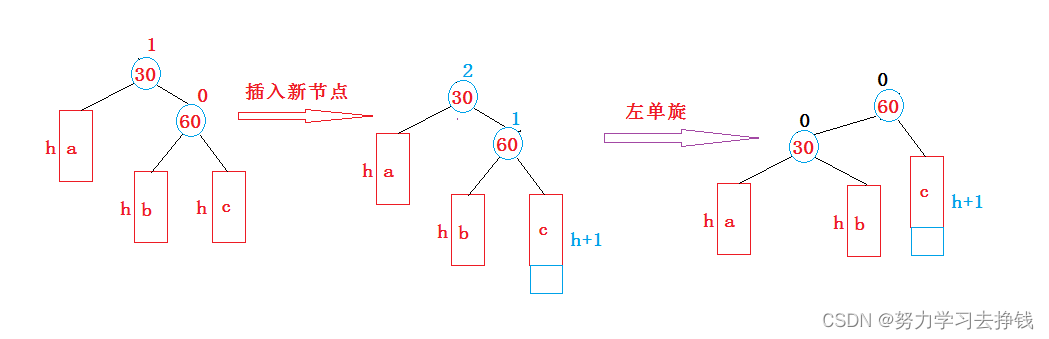
我来解释解释：

上方a代表a整棵子树，b、c同理。h代表树的高度，h >= 0。

未插入节点时，对于30而言，右侧的子树是比左侧的子树高1的。

插入节点之后，也就是插入节点在较高右子树的右侧，此时对于30而言右侧的子树是比左侧的子树高2的，所以此时就要对树进行调整，让30的右侧指向60的左侧，让60的左侧指向30。看起来就像以30的右侧子树节点为轴心，向左旋转，从而使得整个树得到平衡，所以此步也就叫做左单旋。

我们来画几个具体的树看看：

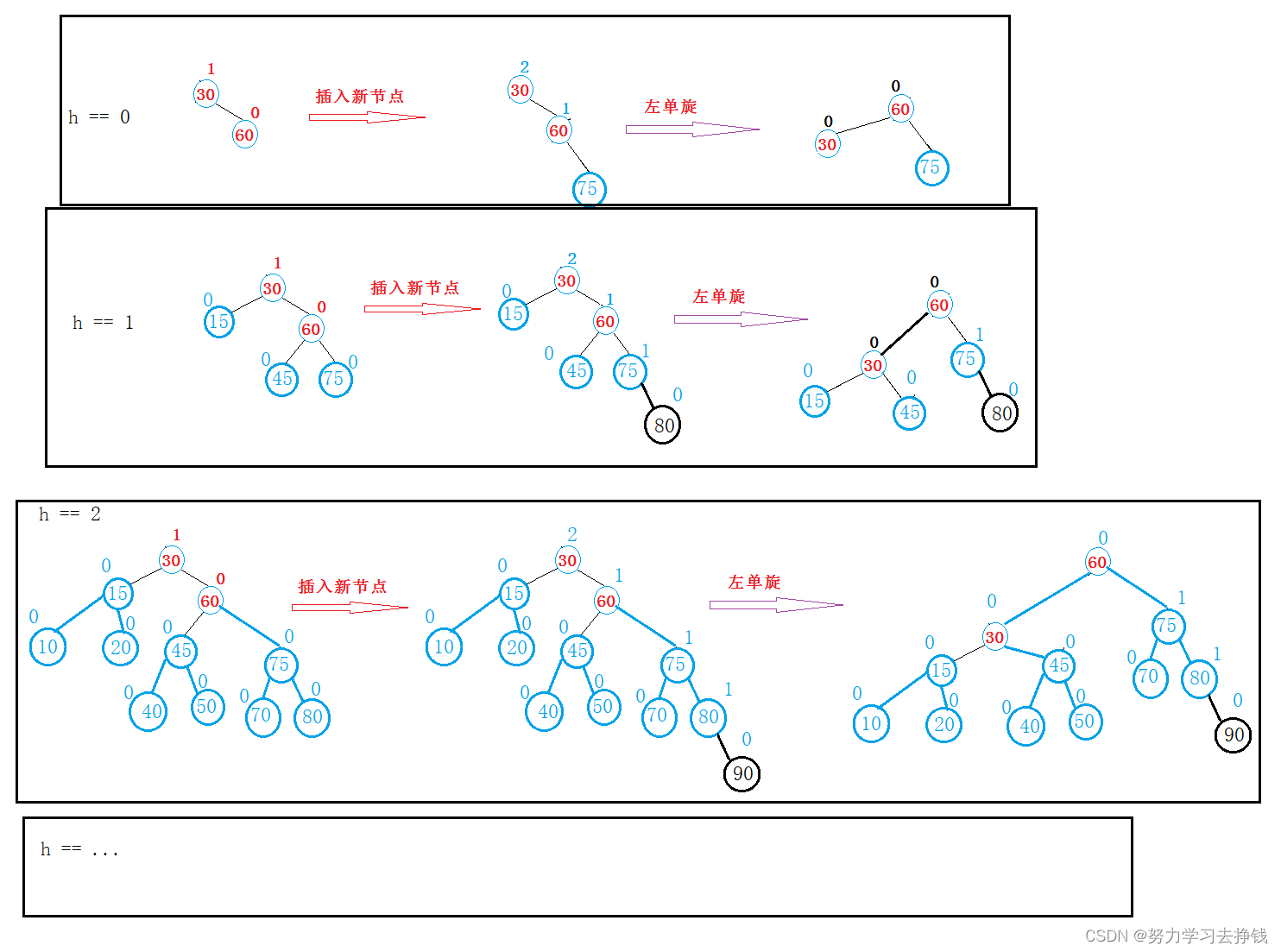
画了三棵树，我已经画不下去了，太麻烦了，方法都是一样的，这里只是把h具体化了出来，如果还有同学没看懂的话，可以自己画画试试，摸索摸索。

这个可以单独写一个函数出来。函数名就是RotateL。

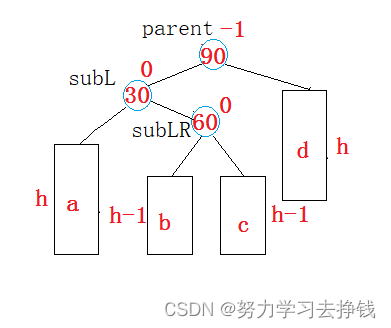
旋转时，可以显示指出两个节点，一个为subR，就是当前parent->_right；一个为subRL，就是当前parent->_right->left。

看图：

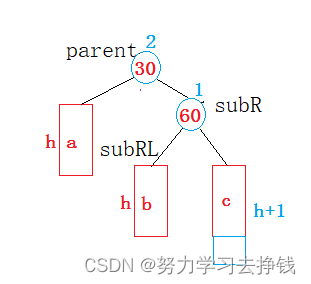
写的时候就是parent->_right = subRL，然后subR->left = parent。

然后就得到平衡树了：

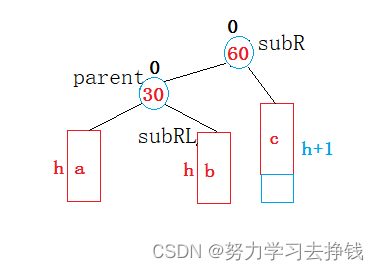
但是还要注意原先30的父节点，如果30本来就是root的话，就要让root指向60，但是不是root的话，就要让30原先的父节点指向60。

记得同时更新变化的节点的父指针。

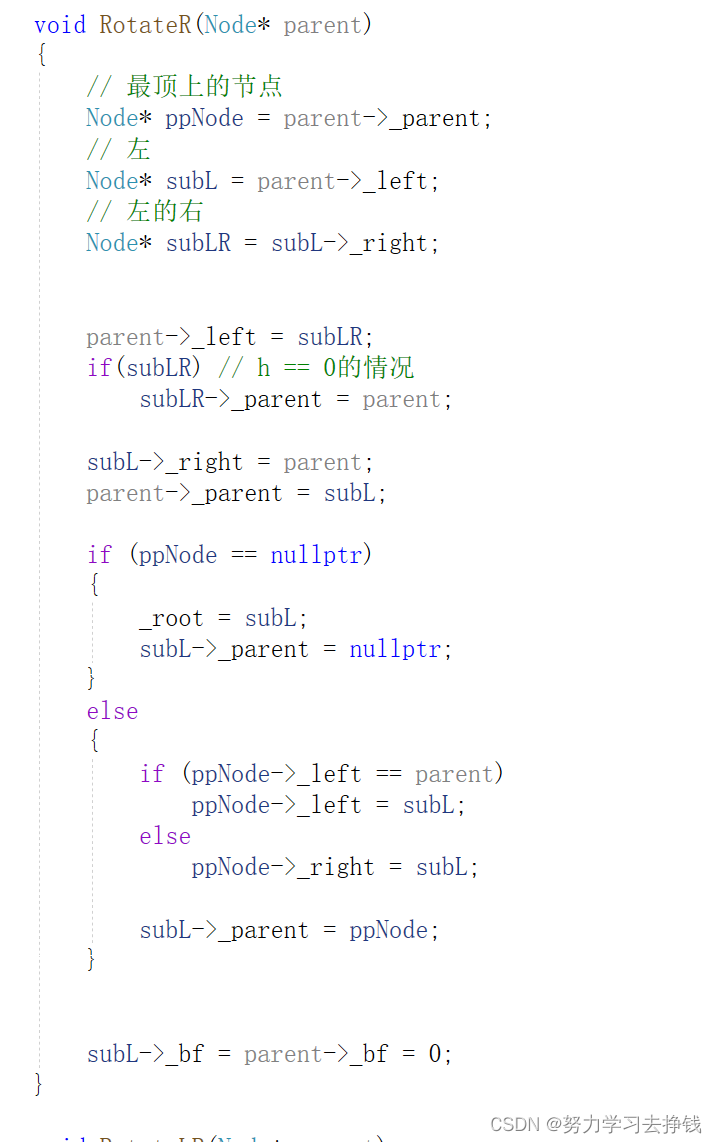
代码如下：

右单旋

新节点插入较高左子树的左侧。即左左。

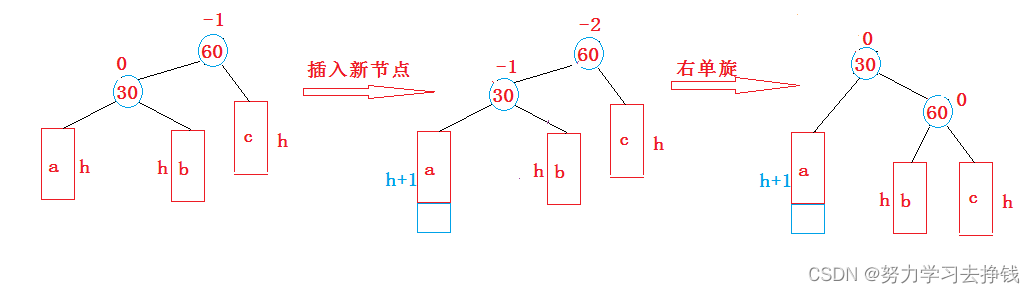
右单旋跟上面的左单旋情况非常相似。

简单说说，未插入新节点时，对于60而言，左侧子树高度比右侧子树高度高1，在30左侧插入节点之后，左侧子树高度比右侧子树高度高2，此时就要进行旋转调整，让30的右给60的左，30的左指向60。看起来就像以30为轴心，向右旋转，从而使得整个树得到平衡，所以此步也就叫做右单旋。

具体的图解就不给了，就和上面左单旋的非常像。不是很理解的同学可以自己画画。

写代码的话，还是显示支出三个节点，一个原树根的父节点ppNode，一个左子树的根subL，一个左子树的右根subRL。

画一下抽象图：

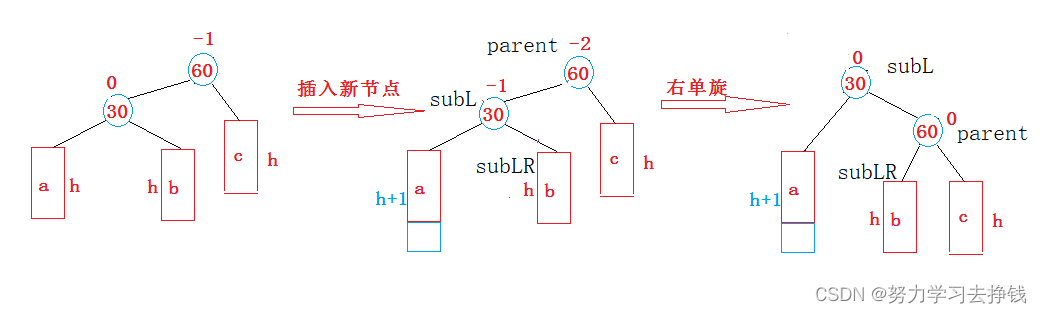
代码如下：

左右双旋

新节点插入再较高左子树的右侧。即左右。

这里就有点讲究了。

首先，插入左子树的右侧还要分更细致一点。

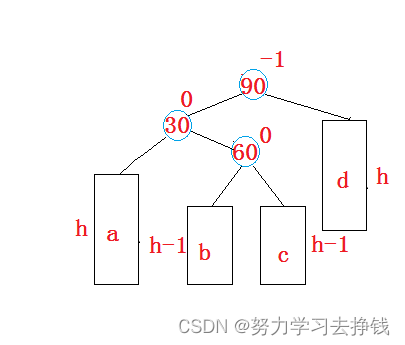
那些字母的意思跟上面的左单旋、右单旋的一样。

但是这里要分三种情况。
第一种，往b树下面插新节点。

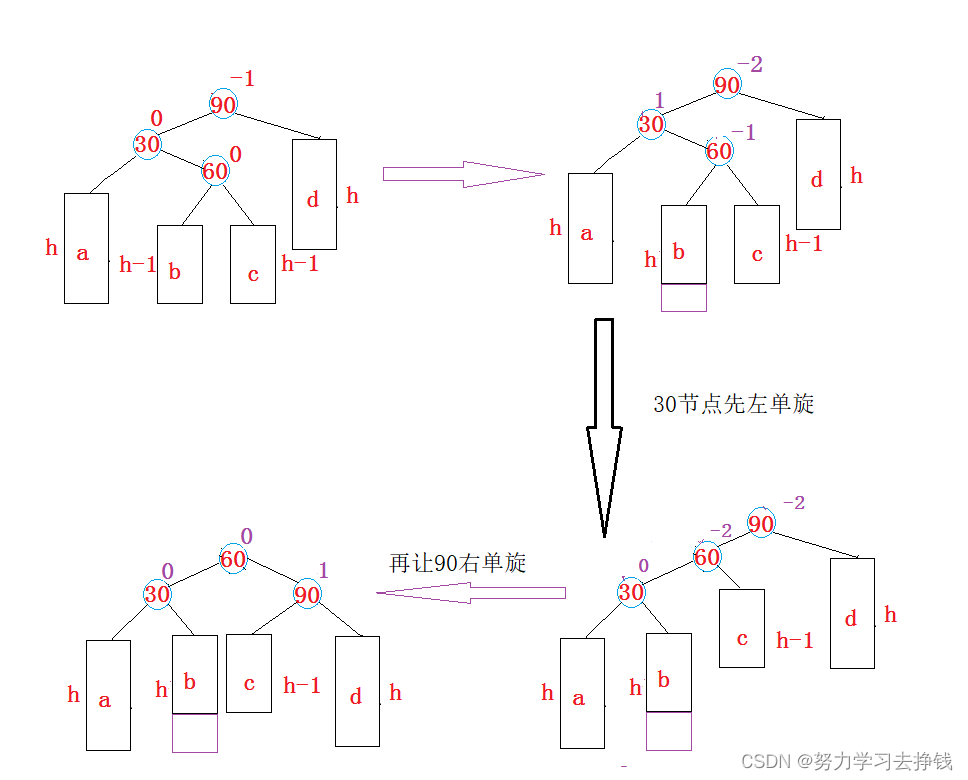
第二种，往c树下面插新节点。

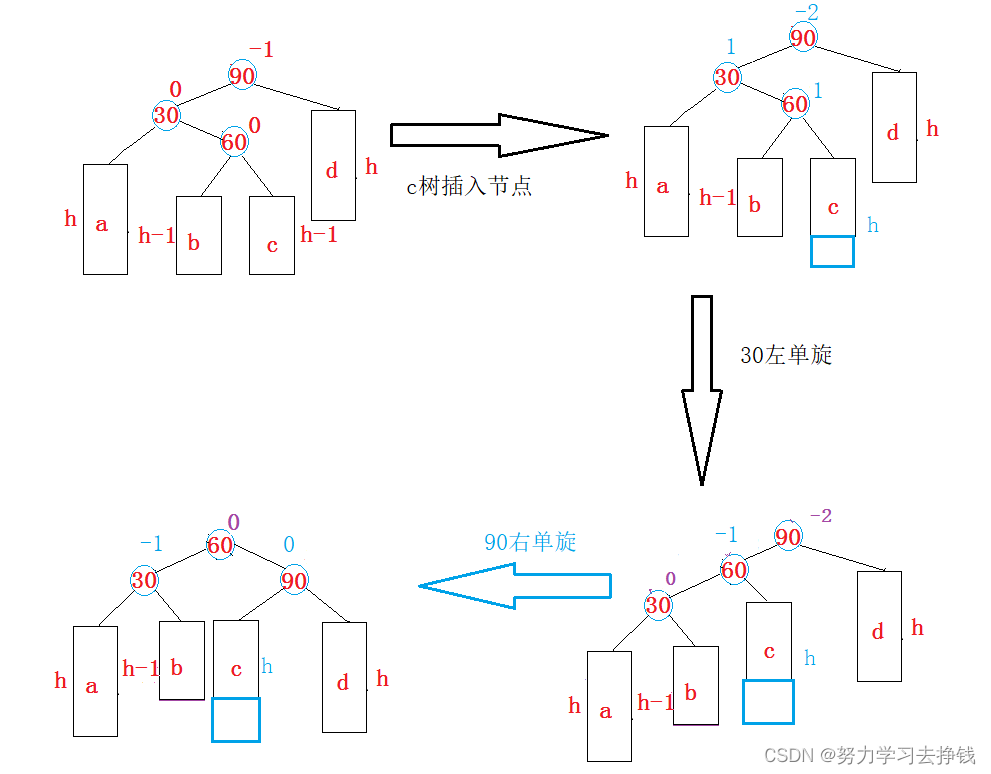
第三种，h == 0，60就是新插入的节点。

就上面三种情况，前两种是抽象的，不懂的同学可以给h一个具体值来自己画画。三种情况下最终根的左右子节点的平衡因子是要分情况讨论的。

而想要分情况讨论的话，就要先找出能够区分出三者的前提条件，这里前提条件就是插入节点之后，也就是旋转之前60的平衡因子。

第一种，往b树下面插新节点，60的平衡因子为-1。
第二种，往c树下面插新节点，60的平衡因子为1。
第三种，h == 0，60的平衡因子为0。

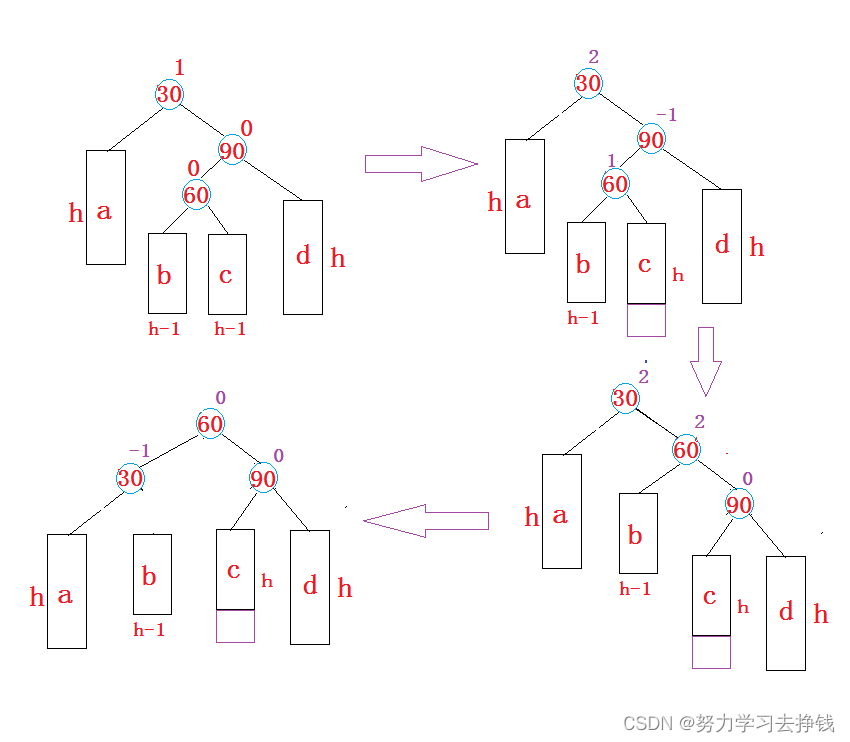
写代码时要显示指出四个节点：subL、subLR。

左旋和右旋的时候只要复用RotateL和RotateR就行了。

所以就可写出如下代码：

上面双旋是让subLR的左右分别给到subL,parent，然后再让subL,parent做subLR的左右护法。

右左双旋

新节点插入在较高右子树的左侧。即右左。

这就跟上面的一样了，就不过多赘述了。也是三种情况，各位自己画画图看你能搞出来不。

我就直接给代码了：

用旋转来平衡树

上面四种旋转情况已经写完了，下面就要用旋转来平衡树了。

续着旋转前insert的代码，我们写到了：

此时就要用到旋转了。

我们可以通过父子节点的平衡因子来判断一棵子树是该左单、右单、左右双、右左双。

上面四种情况中，父与子的bf分别为：

1. 左左是-2，-1
2. 右右是2，1
3. 左右是-2,1
4. 右左是2，-1

根据bf写出如下代码：

测试

先写个中序遍历来测试一下：

测试：

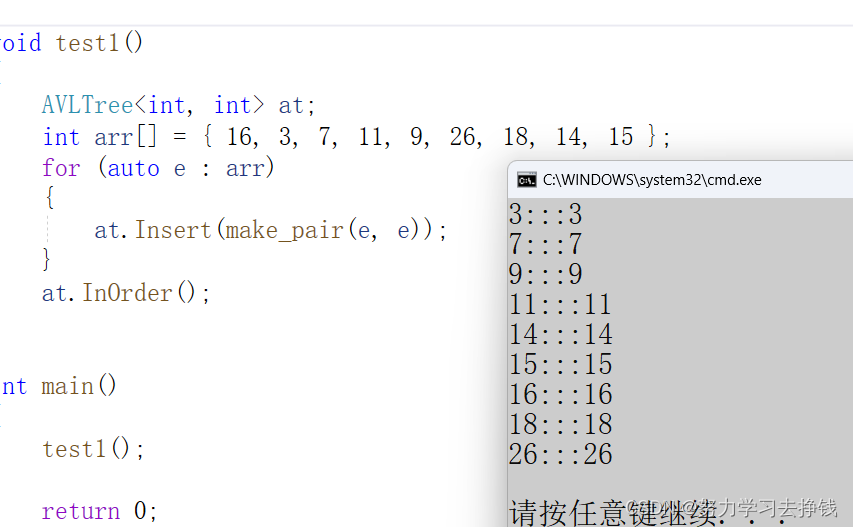
但是光遍历的话不具有说服力。
我们再来写判断是否平衡的函数：

测试：

再来一组：

然后再来一组10000个随机数的：

跑出来10000个数，结果正确。

到这里插入的就都讲完了，本篇就讲这一个功能，删除的话不讲，各位有对删除感兴趣的可以看看其他教学。查找什么的功能都很简单，AVL重在旋转，其他的都是小case，把旋转掌握好，AVL树就拿下了。

到此结束。。。