一、需求

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

提示:

1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1

进阶：

你能尽量减少完成的操作次数吗？

二、思路分析图

（一）递归方案（双指针方案）

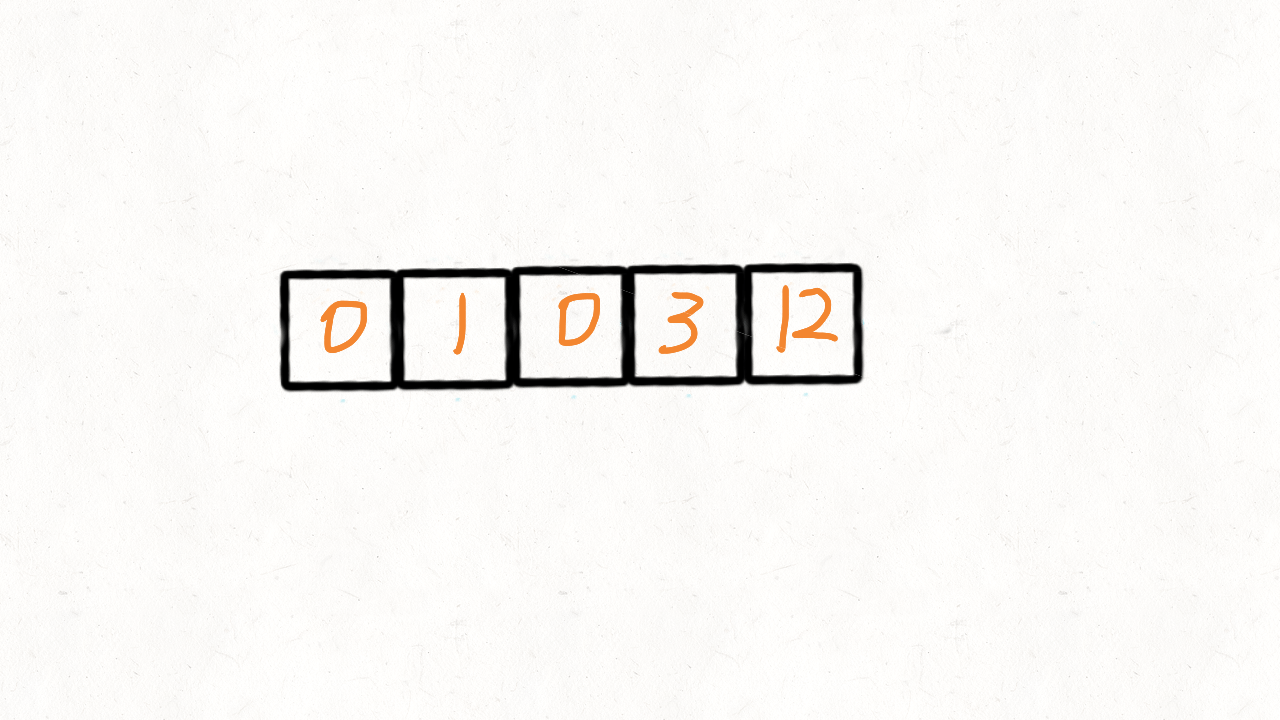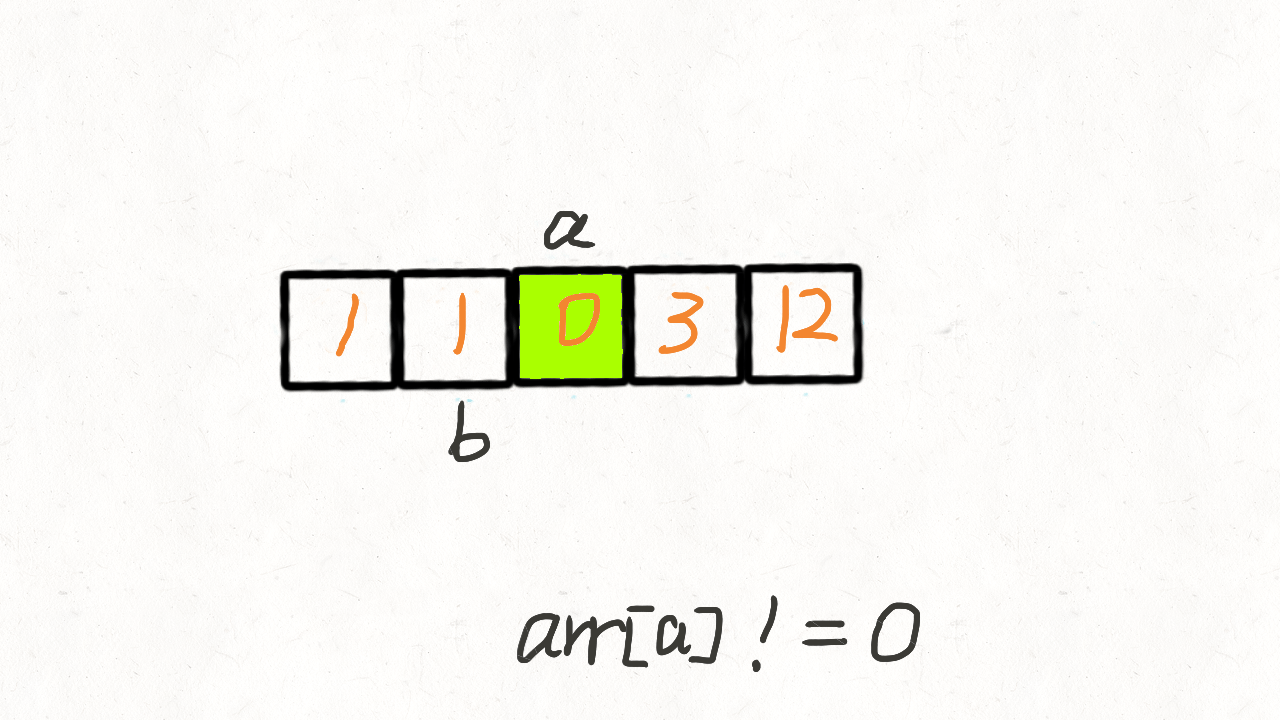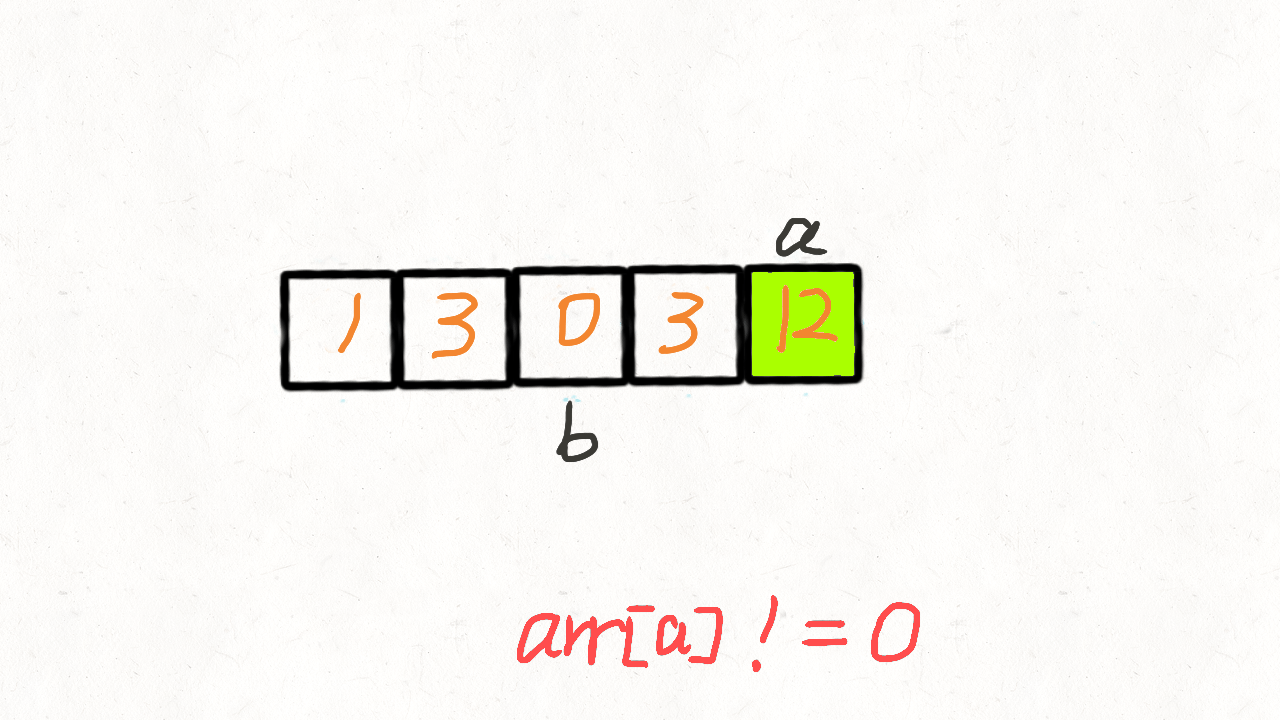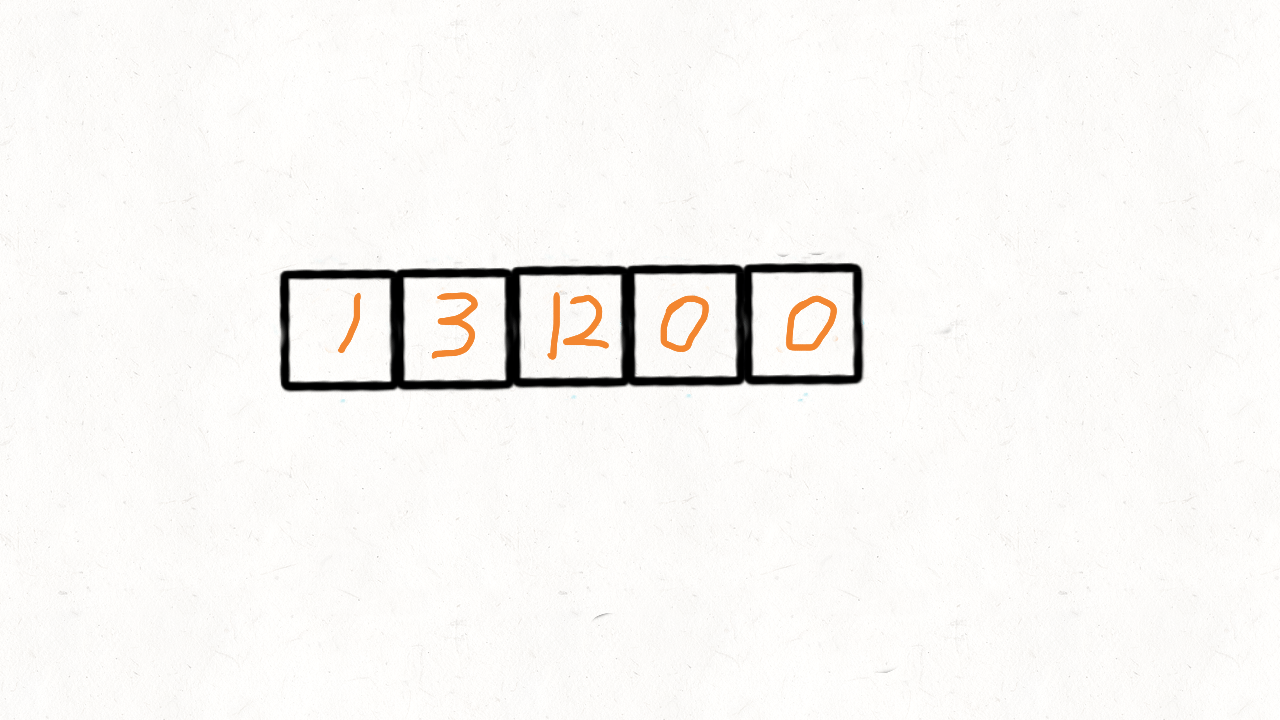
在这里插入图片描述

三、代码

（一）数据初始化

/**
 * 入口
 * 283、移动零
 * 输入：
 * nums = [0,1,0,3,12]
 * 输出：
 * result1 = [1,3,12,0,0]
 * 解释：
 * 1.递归方案
 * 2.O(n)方案
 */
@Test
public void suanfa40()
{
    // 初始化
    int[] nums1 = {0, 1, 0, 3, 12};
    int[] nums2 = {0, 1, 0, 3, 12};

    // 打印
    // 迭代方案【自己写的方案】
    int[] result1 = this.for2MoveZeroes(nums1);
    System.out.println("result1 = " + result1);
    Arrays.stream(result1).forEach(System.out::println);

    // 迭代方案【O(n)方案】
    int[] result2 = this.for1MoveZeroes(nums2);
    System.out.println("result2 = " + result2);
    Arrays.stream(result2).forEach(System.out::println);
}

（二）递归方案【自己写的方案】

/**
 * 迭代方案【自己写的方案】
 *
 * @param nums
 * @return
 */
public int[] for2MoveZeroes(int[] nums)
{
    int numsLength = nums.length - 1;
    int j = 0;
    int temp = 0;
    // A B
    for (int i = 0; i <= numsLength; i++)
    {
        // A == 0
        if(nums[i] == 0)
        {
            j = i + 1;
            while (j <= numsLength)
            {
                if (nums[j] == 0)
                {
                    j++;
                }
                else
                {
                    temp = nums[i];
                    nums[i] = nums[j];
                    nums[j] = temp;
                    j += numsLength;
                }
            }
        }
    }
    return nums;
}

（三）递归方案【O(n)方案】

/**
 * 迭代方案【O(n)方案】
 *
 * @param nums
 * @return
 */
public int[] for1MoveZeroes(int[] nums)
{
    // 先处理非0参数，j就是按循序记录
    int j = 0;
    for (int i = 0; i < nums.length; i++)
    {
        if (nums[i] != 0)
        {
            nums[j] = nums[i];
            j++;
        }
    }
    return nums;
}