【递归算法实践】验证二叉搜索树

news2024/9/20 5:55:32

1. 递归算法

2. 递归实现验证二叉搜索树

3. 递归解法的实现逻辑

4. 递归实现的实例分析

1. 递归算法

递归是一种通过函数自身调用来解决问题的算法，它可以使代码更加简洁和优雅，同时也能够解决许多复杂的问题。在递归中，函数会不断地调用自身来解决一个更小的问题，直到达到基本情况为止。

递归算法（recursion algorithm）在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。递归式方法可以被用于解决很多的计算机科学问题，因此它是计算机科学中十分重要的一个概念。

2. 递归实现验证二叉搜索树

题目：

https://leetcode.cn/problems/validate-binary-search-tree/

https://leetcode.com/problems/validate-binary-search-tree/

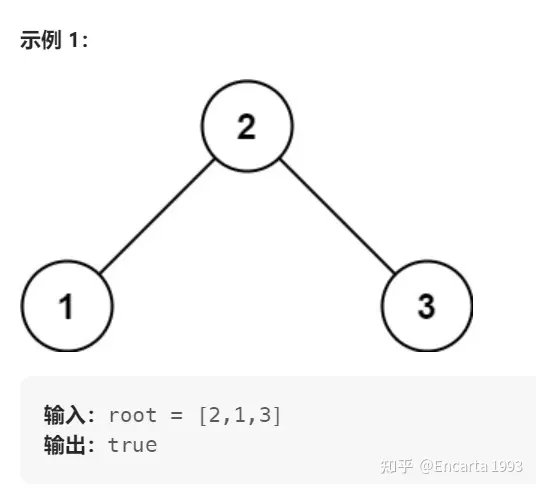
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

代码实现：

from typing import Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:

    def __init__(self) -> None:
        self.pre = float("-inf")

    # inorder traversal
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        if root is None :
            return True
        # 一直递进左子树中，直到遇到 None，这时候发生第一次的回归，
        # 然后执行下面几行代码，即进行值的判断，并且递进到右子树中，
        # 接着按照递进的反方向一层一层的回归
        if not self.isValidBST(root.left):
            return False
        if root.val <= self.pre:
            return False
        self.pre = root.val
        return self.isValidBST(root.right)

if __name__ == "__main__":
    solution = Solution()

    # a = TreeNode(4)
    root = TreeNode(0)
    # c = TreeNode(3)

    # root.left = a
    # root.right = c

    result = solution.isValidBST(root)
    print(result)

3. 递归解法的实现逻辑

`isValidBST` 方法中，先判断当前节点是否为 None，如果是则返回 True，表示当前子树是一个有效的 BST。接着，递归判断左子树是否为 BST，如果不是则返回 False。然后，判断当前节点的值是否小于等于上一个节点的值 `pre`，如果小于等于则返回 False。最后，将当前节点的值赋值给 `pre`，递归判断右子树是否为 BST，如果不是则返回 False。

如果以上条件都满足，则该二叉树是一个有效的 BST，返回 True。

在 `isValidBST` 方法中，如果左子树或右子树不是 BST，则返回 False，而不是返回 True，是因为在判断一个二叉树是否为 BST 时，只要发现它的左子树或右子树不是 BST，就可以确定该二叉树不是 BST，不需要再继续遍历下去了。

如果在左子树或右子树中发现了一个不符合 BST 的节点，那么它的父节点及其祖先节点都不可能是 BST，因为 BST 的定义要求左子树的所有节点都小于根节点，右子树的所有节点都大于根节点。因此，如果左子树或右子树不是 BST，就可以直接返回 False，不需要再继续遍历下去了，这样可以提高程序的效率。

4. 递归实现的实例分析

`isValidBST`函数是一个验证二叉搜索树的函数。下面使用一个例子来逐步解释递归的执行流程和代码实现思路。

假设我们有以下二叉树：

```
5
/ \\
1 7
/ \\
6 8
```

我们首先调用`isValidBST`函数，传入根节点`5`。由于`root`不为空，我们继续执行函数。由于`root`有左子节点`1`，我们递归调用`isValidBST`函数，传入`1`作为参数。由于`1`没有左子节点或右子节点，我们直接返回`True`。此时，我们回到了根节点`5`的函数调用。

由于`root`有左子节点，我们刚刚递归调用了`isValidBST`函数，它会返回`True`。我们继续执行函数，检查`root`的值是否大于前一个节点的值。由于这是第一个节点，前一个节点的值为负无穷，所以这个条件满足。我们将`pre`的值设置为`5`，然后继续执行函数。

由于`root`有右子节点`7`，我们递归调用`isValidBST`函数，传入`7`作为参数。由于`7`有左子节点`6`，我们继续递归调用`isValidBST`函数，传入`6`作为参数。由于`6`没有左子节点或右子节点，我们直接返回`True`。此时，我们回到了节点`7`的函数调用。

由于`7`的左子节点`6`已经处理完毕，我们继续执行函数，检查`root`的值是否大于前一个节点的值。由于`7`大于`5`，这个条件满足。我们将`pre`的值设置为`7`，然后继续执行函数。

由于`7`有右子节点`8`，我们递归调用`isValidBST`函数，传入`8`作为参数。由于`8`没有左子节点或右子节点，我们直接返回`True`。此时，我们回到了节点`7`的函数调用。

由于`root`的右子树已经处理完毕，我们回到了根节点`5`的函数调用。由于根节点`5`的左子树和右子树都已经处理完毕，且满足二叉搜索树的定义，所以整个函数返回`True`，表示这棵二叉树是一棵合法的二叉搜索树。

这段代码的实现思路是，对于每个节点，都检查它是否大于前一个节点的值。由于二叉搜索树的中序遍历是有序的，前一个节点的值应该小于当前节点的值。如果出现了前一个节点的值大于当前节点的值的情况，说明这棵二叉树不是一棵合法的二叉搜索树。