关于严谨性的声明:
在用C语言进行定积分的计算之前,我需要声明以下几点:
一、我们所进行定积分计算的函数都是应当是黎曼可积的,这保证了我们即使均匀地分割区间也保证了积分的收敛性。
二、我们同时还应该认识到,鉴于某些函数不一定是在每一点上都是可导的,因此我们将不使用所谓的利用到导数来提高计算精度的这种算法。
三、考虑到某些函数并不是连续的,如果涉及到这些计算,那么我们计算到的结果将会是一个瑕积分,如果这个瑕积分是收敛的,那么我们得到的就是收敛值。如果不收敛,这个瑕积分的值并不是积分主值,因为我们没有办法保证瑕点附近的两个点的趋近于瑕点的趋势是一样的。
四、如果你计算的是一个无穷积分,如果这个无穷积分是收敛的,那么我们得到的就是收敛值。如果不收敛,那么我们得到的值将会是它的积分主值。
另外,考虑到C语言精度的限制,我们无需写一个专门的程序用来计算瑕积分,因为当我们用C语言计算这个瑕积分的时候,就相当于我们采用了两边趋近瑕点取极限的办法来计算瑕积分,当然了,由于我们采用了均匀分割的方法,所以当我们两边趋近的时候并不能使得其以任意方式趋近瑕点。除此之外,你应当保证瑕点不在积分区间的边界上。对于无穷积分,不论我们怎么切割区间都不能使得划分的区间足够小,除非我们划分区间的时候将他划为了无穷份,当然了这个划分的份数应当是无穷积分区间大小的高阶无穷大。事实上,这是做不到的,因此我们将采用函数变换的方法将无穷积分转化为有限积分。
最后,鉴于C语言的精度限制,如果我们只是计算性质较为良好的函数,那么我们将会获得非常好的精度,甚至是仅仅只是可测的函数,也是可以计算的。但如果我们计算的是有着许多无穷间断点,或有着许多瑕点的函数,或者是震荡很厉害的函数,那么它的积分值误差将会较大。最后我还想声明一点,那就是我们不应该用该程序去计算本身就是发散的积分因为你甚至可能得到的仅仅只是个有限值。
1. 有限积分
根据我们在之前所说的,我们可以轻易得到:
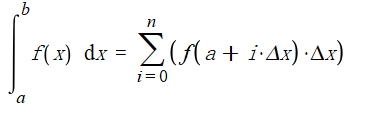
其中:
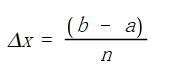
因此,我们不难写出以下代码:
//定义一个C语言函数,用于进行微积分的数值运算
long double integrate(long double a, long double b, long int n)
{
long double s = 0;
long double dx = (b - a) / n;
for (long int i = 1; i < n; i++)
{
s += f(a + i * dx) * dx;
}
return s;
}其中函数 long double integrate(long double a, long double b, long int n) 就是用来计算定积分的函数。值得注意的是,在调用该函数之前,我们应当提前定义被积函数f(x)。其中a,b,n分别为积分下限,积分上限和区间分割数。
以上是矩形法,数值计算的精度并不是非常高,我们改进一下,使用梯形法,得到:
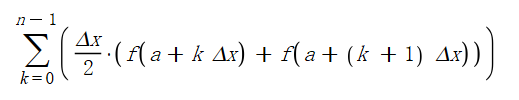
其中:
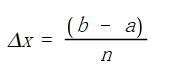
因此,我们不难写出以下代码:
long double integral(long double x0, long double xt, long long n)
{
long double sum = 0;
long double dx = (xt - x0) / n;
for (long long k = 0; k < n; k++)
{
sum += ((f(x0 + k * dx) + f(x0 + (k + 1) * dx)) / 2) * dx;
}
return sum;
}相较于矩形法,梯形法不论是精度还是速度都有着不小的提升。
2. 无穷积分
我们已经讨论过无穷积分采用直接计算的困难的地方,因此我们将采用函数变换的方法。
我们很容易注意到:
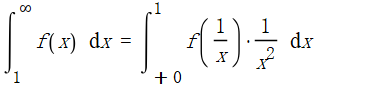
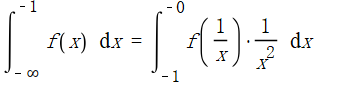
这两个式子是等价的,因此我们可以将所有的无穷积分转化为无限积分。只需要利用积分区间的可叠加性即可。因此不多叙述。
有了相关的理论铺垫后,我们添加一点点细节。以下直接给出关于定积分的计算代码:(详细信息在注释里)
#include <stdio.h>
#include <math.h>
#define inf INFINITY
// 定义用于被积分的函数
long double f(long double x)
{
return exp(x);
}
// 定义被积函数的特殊形式用于计算无穷积分
long double g(long double x)
{
long double y = 1.0 / x;
long double result = f(y) * (1.0 / (x * x));
return result;
}
// 一个用于计算定积分的C语言子程序
//值得注意的是我们还将数学函数作为参数传给了这个函数,这可以让我们有多个数学函数时,可以指定数学函数计算
long double integral(long double x0, long double xt, long long n, long double (*f)(long double))
{
//对于黎曼可积的函数,这样的积分值为零,直接返回。
if ((x0 == xt)&&((x0 != INFINITY && x0 != -INFINITY)&&(xt != INFINITY && xt != -INFINITY)))
return 0;
else
{
long double sum = 0;
long double dx = (xt - x0) / n;
for (long long k = 0; k < n; k++)
{
sum += ((f(x0 + k * dx) + f(x0 + (k + 1) * dx)) / 2) * dx;
}
return sum;
}
}
// 定义绝对值函数
static long double lfabs(long double x)
{
if (x >= 0)
return x;
else
return -x;
}
//用于计算指定精度的定积分的函数
//值得注意的是我们还将数学函数作为参数传给了这个函数,这可以让我们有多个数学函数时,可以指定数学函数计算
long double definite_integral(long double x0, long double xt, long double esp, long double (*f)(long double))
{
//如果积分限不是无穷则进行经典数值积分计算
if ((x0 != INFINITY && x0 != -INFINITY) && (xt != INFINITY && xt != -INFINITY))
{
long long i = 10;
long double d = 0;
long double s = 0;
do {
long double s1 = integral(x0, xt, i, f);
long double s2 = integral(x0, xt, 10 * i, f);
i *= 10;
s = s2;
d = lfabs(s1 - s2);
} while (d > esp);
return s;
}
//如果是无穷积分,则采用特殊方法进行数值计算
else
{
//积分下限有限大小
//值得注意的是,当我们使用g函数进行积分的时候,有一个积分限迎丹是0,然而事实上我们以一个很小的小数来替代
if (x0 != INFINITY && x0 != -INFINITY)
{
if (xt == INFINITY)
{
long double s1 = definite_integral(x0, 1, esp, f);
long double s2 = definite_integral(esp/1000000.0, 1, esp, g);
return (s1 + s2);
}
else if (xt == -INFINITY)
{
long double s1 = definite_integral(-1, x0, esp, f);
long double s2 = definite_integral(-1, -esp/1000000.0, esp, g);
return -(s1 + s2);
}
}
//积分上限有限大小
else if (xt != INFINITY && xt != -INFINITY)
{
if (x0 == INFINITY)
{
long double s1 = definite_integral(xt, 1, esp, f);
long double s2 = definite_integral(esp/1000000.0, 1, esp, g);
return -(s1 + s2);
}
else if (x0 == -INFINITY)
{
long double s1 = definite_integral(-1, xt, esp, f);
long double s2 = definite_integral(-1, -esp/1000000.0, esp, g);
return (s1 + s2);
}
}
//积分上下限都为无穷
else if (x0 == -INFINITY && xt == INFINITY)
{
long double s1 = definite_integral(-1, 1, esp, f);
long double s2 = definite_integral(-1, -esp/1000000.0, esp, g);
long double s3 = definite_integral(esp/1000000.0, 1, esp, g);
return (s1 + s2 + s3);
}
else if (x0 == INFINITY && xt == -INFINITY)
{
long double s1 = definite_integral(-1, 1, esp, f);
long double s2 = definite_integral(-1, -esp/1000000.0, esp, g);
long double s3 = definite_integral(esp/1000000.0, 1, esp, g);
return -(s1 + s2 + s3);
}
//如果积分是从正无穷积分到正无穷或从负无穷积分到负无穷则需要另外判断
else
{
if (x0 == INFINITY && xt == INFINITY)
{
if (f(INFINITY) == 0)
return 0;
else
return NAN;
}
else if (x0 == -INFINITY && xt == -INFINITY)
{
if (f(-INFINITY) == 0)
return 0;
else
return NAN;
}
}
return NAN;
}
}
int main()
{
long double x0, xt, esp;
printf("如果要输入无穷大或无穷小,请输入inf或-inf\n");
printf("请输入积分区域(x0,xt),和最大容忍误差esp:>>");
scanf("%lf %lf %lf", &x0, &xt, &esp);
long double result = definite_integral(x0, xt, esp, &f);
printf("%.16lf\n", result);
return 0;
}在计算指定定积分精度的C函数中,对于无穷积分我们通过转化为有限积分后再调用自身的方式有效地减伤了大量大代码量。这也是为什么要把我们定义的数学函数作为参数传给函数的原因。
如下:
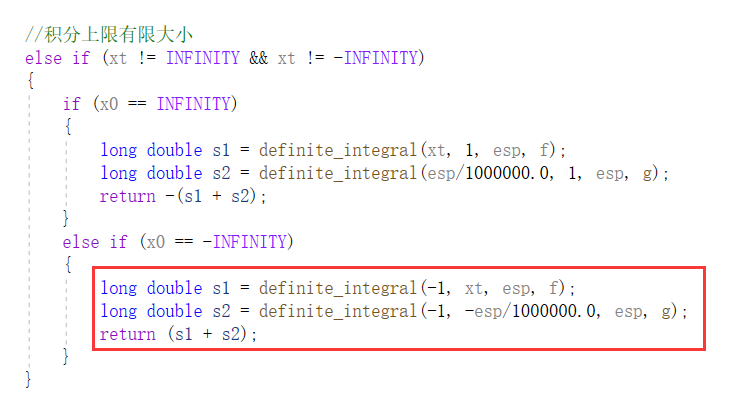
代码的运行:
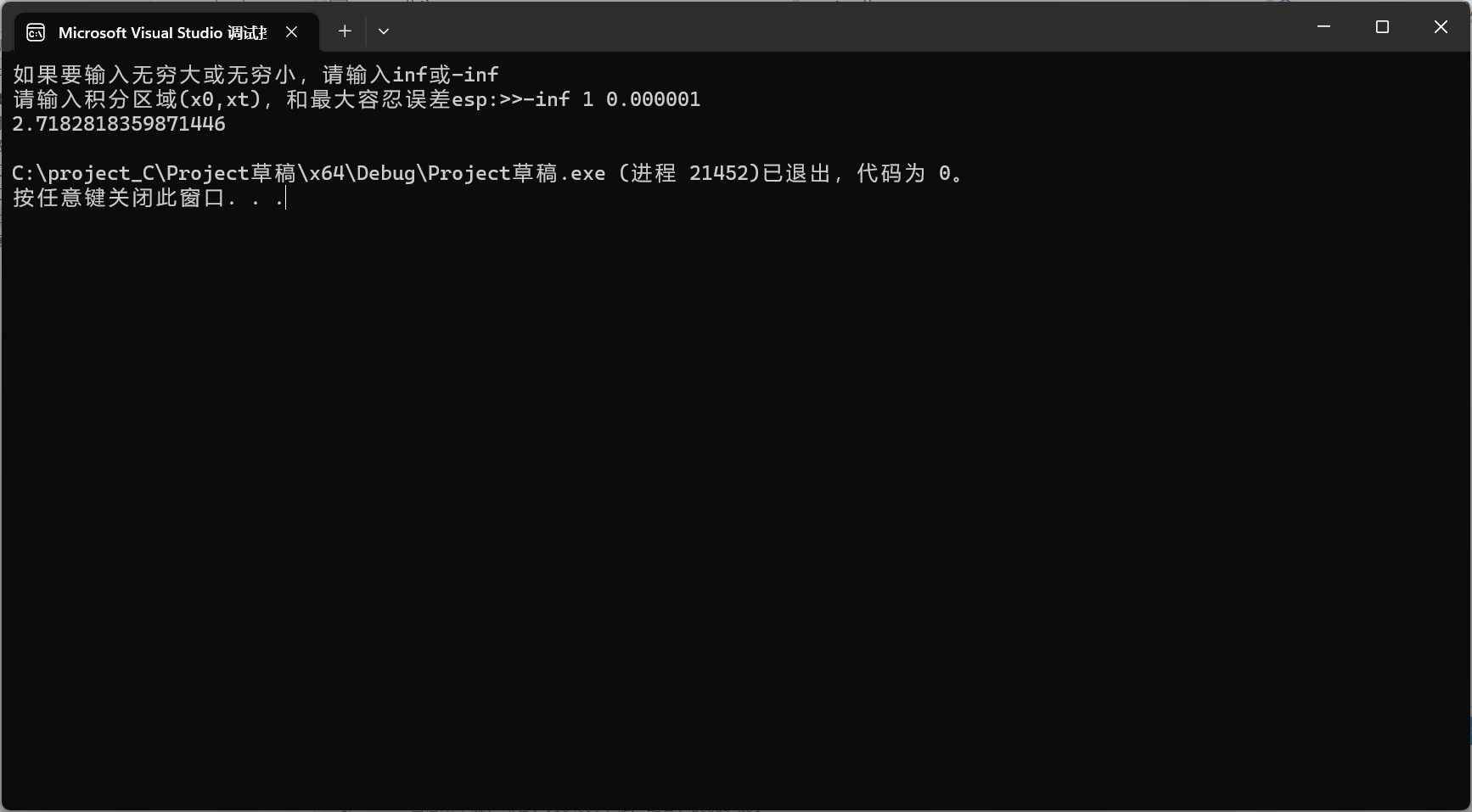
我们指定数学函数为exp(x),可以看到我们很好地计算出来该无穷积分。