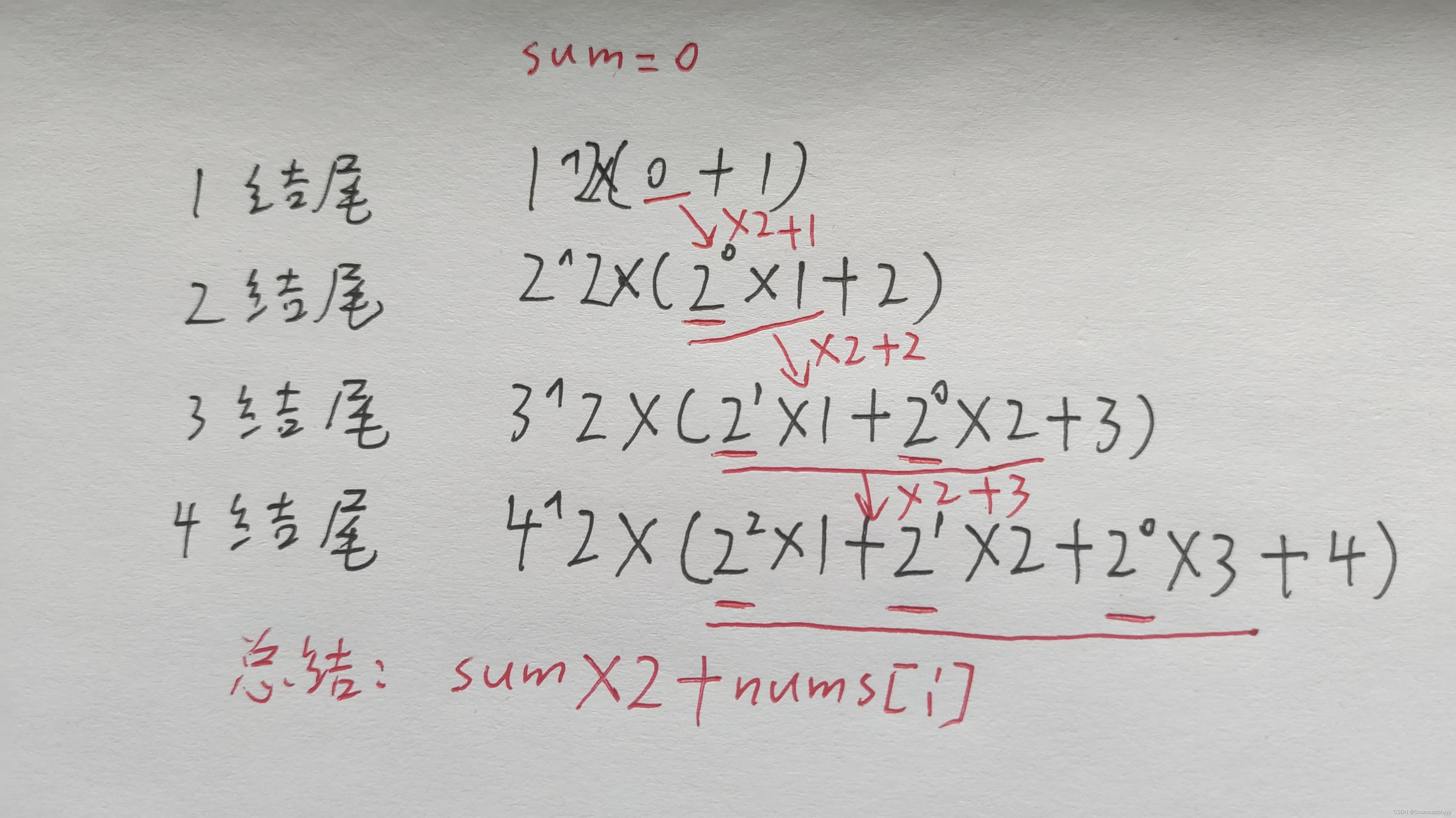2681. 英雄的力量

题目描述：

给你一个下标从 0 开始的整数数组 nums ，它表示英雄的能力值。如果我们选出一部分英雄，这组英雄的力量定义为：

i0 ，i1 ，... ik 表示这组英雄在数组中的下标。那么这组英雄的力量为 max(nums[i0],nums[i1] ... nums[ik])2 * min(nums[i0],nums[i1] ... nums[ik]) 。

请你返回所有可能的非空英雄组的力量之和。由于答案可能非常大，请你将结果对 109 + 7 取余。

示例 1：

输入：nums = [2,1,4]
输出：141
解释：
第 1 组：[2] 的力量为 2^2 * 2 = 8 。
第 2 组：[1] 的力量为 1^2 * 1 = 1 。
第 3 组：[4] 的力量为 4^2 * 4 = 64 。
第 4 组：[2,1] 的力量为 2^2 * 1 = 4 。
第 5 组：[2,4] 的力量为 4^2 * 2 = 32 。
第 6 组：[1,4] 的力量为 4^2 * 1 = 16 。
第 7 组：[2,1,4] 的力量为 4^2 * 1 = 16 。
所有英雄组的力量之和为 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141 。

示例：

输入：nums = [1,1,1]
输出：7
解释：总共有 7 个英雄组，每一组的力量都是 1 。所以所有英雄组的力量之和为 7 。

实现代码与解析：

数学规律

class Solution {
public:
    int mod = 1e9 + 7;
    int sumOfPower(vector<int>& nums) {

        sort(nums.begin(), nums.end());
        long long res = 0, sum = 0;

        for (int i = 0; i < nums.size(); i++)
        {
            res = (res + (long long)nums[i] * (long long)nums[i] % mod * (nums[i] + sum)) % mod;
            sum = (sum * 2 + nums[i]) % mod; 
        }
        return res;
    }
};

原理思路：

分析题目，可以发现，其实英雄能力值之和每个子集的最大值和最小值有关，所有我们先sort排序，然后遍历，让其作为最大值，这是固定的，所以只要找出以 nums[ i ] 为最大值结尾的子集的最小值的和与最大值的平方相乘就得出了此种情况的英雄力量的和，最后全加起来，就得到了答案。

所以关键的核心就时如何求出以 nums[ i ] 为最大值结尾的子集的最小值的和。

比如排序后{1， 2， 3， 4}，当遍历到4时，以其为最大值的子集有多少种？

当选择1为最小值时，2可选可不选，3可选可不选，这样就是2 * 2 = 4 个，4 * （4 * 4）* 1就为一组力量值。可以发现一组力量值是和元素的个数和最小值有关的。

那么我们可以总结出递推式，之间算出一个最大值平方需要乘的总和为：sum(nums[i] * 2 ^ 最小值与最大值中间的数字个数)，i 从 0 到最大值下标。

这样就可以发现子集最小值总和明显是可以根据前一个的子集最小值总和算出来的。规律如下：