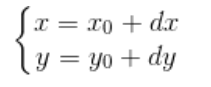如果你觉得这篇题解对你有用，可以点个赞或关注再走呗，谢谢你的关注~

分析

最大异或对

(1)最大异或对是运用trie树存储十进制数对应的二进制数的每一位。
(2)再根据trie树的每一位进行搜索查找，严格满足不同的数异或为1，相同的异或为0。
(3)根据(2)进行搜索，从最高位开始搜索，尽可能地保证较高位次的异或数最大。

通过搜索，匹配每个位最大的异或数。

即从最高位开始,尽可能多地保证每一位的异或数为1，要保证这一点，就需要往当前位数不同的方向走，这样所得到的结果最大。

换句话来说，从最高位开始，往当前位数不同的方向走，如0往1，1往0的方向走，实在无不同位数就走相同位数。

trie结果唯一及确保选取两个数

query一个数的时候，这时该数会根据之前插进trie树的每个数的二进制数进行搜索，直至搜到叶子节点，结果唯一，那这样就保证我们是选择了两个数去进行异或操作，最后得到唯一的最大值。

注意!

理论上，先插入再查找和先查找再插入均可。
但在实现时，考虑到边界问题，即最开始树为空时，查找的边界问题。
采用先插入再查找的方式实现,trie数左节点为0，右节点为1。

分析图

模拟

在这里插入图片描述

res+=1<<i

在这里插入图片描述

注：把异或数为1的数位左移1相当于2的i次方，再把每次枚举的每个位置的结果加起来，就可以得出最大值。

trie树在数组的体现

在这里插入图片描述

ACcode

import java.io.*;
public class Main{
    static int N=3100010;
    //总共是10000个数，每个数枚举对应二进制数的30个位置
    //所以总共是31000010个数
    //数组开小的话为MLE
    static int idx;
    static int son[][]=new int [N][2];
    //一定要记得是0\1两列 p到0和p到1
    public static void insert(int x){
        int p=0;
        for(int i=30;i>=0;i--){
            int u=x>>i&1;
            if(son[p][u]==0)son[p][u]=++idx;
            p=son[p][u];
        }
    }
    public static int query(int x){
        int p=0,res=0;
        for(int i=30;i>=0;i--){
            int u=x>>i&1;
            if(son[p][1-u]!=0){
                res+=1<<i;
                p=son[p][1-u];
            }
            else{
                p=son[p][u];
            }
        }
        return res;
    }
    public static void main(String []args)throws IOException{
        BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw=new PrintWriter(new OutputStreamWriter(System.out));
        String str[]=bf.readLine().split(" ");
        int n=Integer.parseInt(str[0]);
        String s[]=bf.readLine().split(" ");
        for(int i=0;i<n;i++)
        {
            insert(Integer.parseInt(s[i]));
        }
        int res=0;
        for(int i=0;i<n;i++){
        int t=query(Integer.parseInt(s[i]));
        res=Math.max(res,t);
    }
    pw.println(res);
    pw.flush();
}
}

详解代码

import java.io.*;
public class Main{
    static int N=3100010;
    static int idx;
    static int son[][]=new int [N][2];
    public static void main(String []args)throws IOException{
    BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    int n = Integer.parseInt(in.readLine());
    String s[]=in.readLine().split(" ");
    for(int i=0;i<n;i++){
        insert(Integer.parseInt(s[i]));
    }
    int res=0;
    for(int i=0;i<n;i++){
        int t = query(Integer.parseInt(s[i]));
        res=Math.max(res,t);
    }
    out.write(res+" ");
    out.close();
    }
    
    public static void insert(int x){
        int p=0;
        for(int i=30;i>=0;i--){
            int u=x>>i&1;//取出二进制数的第i位
            if(son[p][u]==0)son[p][u]=++idx;//如果还未被创建，则进行建边操作，连接两个节点，即++idx
            p=son[p][u];//往下一层走
            
        }
    }
    public static int  query(int x){
        int p=0,res=0;
        for(int i=30;i>=0;i--){
            int u=x>>i&1;
            if(son[p][1-u]!=0){
                //当u=0时，即1-0=1，往1的方向走，异或值最大。
                //son[p][1-u]用来确定1方向的
                //点是否存在，存在则进行下面操作
                //不存在则只能选择唯一的路来走
                
                //当u=1时，即1-1=0，往0的方向走，异或值最大。
                //son[p][1-u]用来确定1方向的点是否存在，存在则进行下面操作
                //不存在则只能选择唯一的路来走
                
                res+= 1<<i;//1<<i = 1 *2的i次方
                //if分支内得到的异或数为1，加上。
                //else分支内得到的异或数为0，不需要加上。
                
                p=son[p][1-u];//以此进入下一层
                
            }
            else{
                //只能选择下面唯一的路来做
                p=son[p][u];
                
            }
        }
        
        return res;
    }
    
    
}