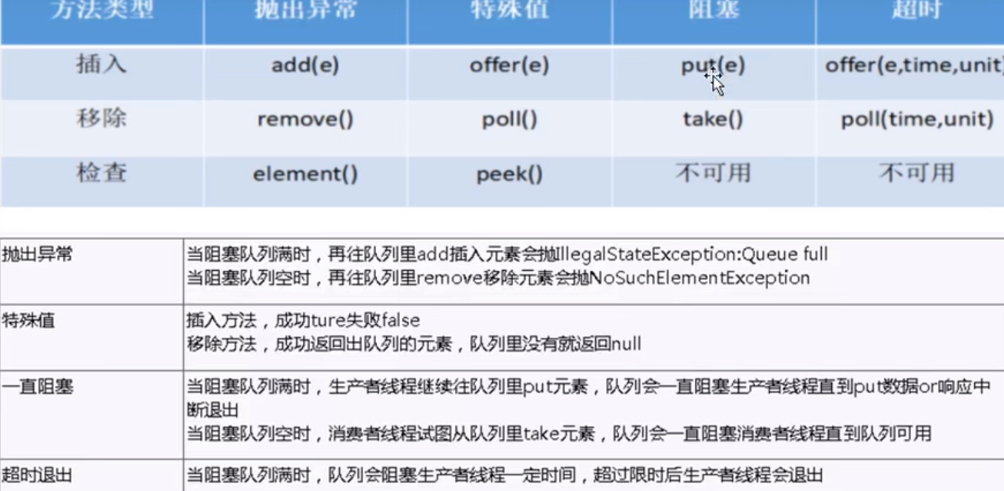
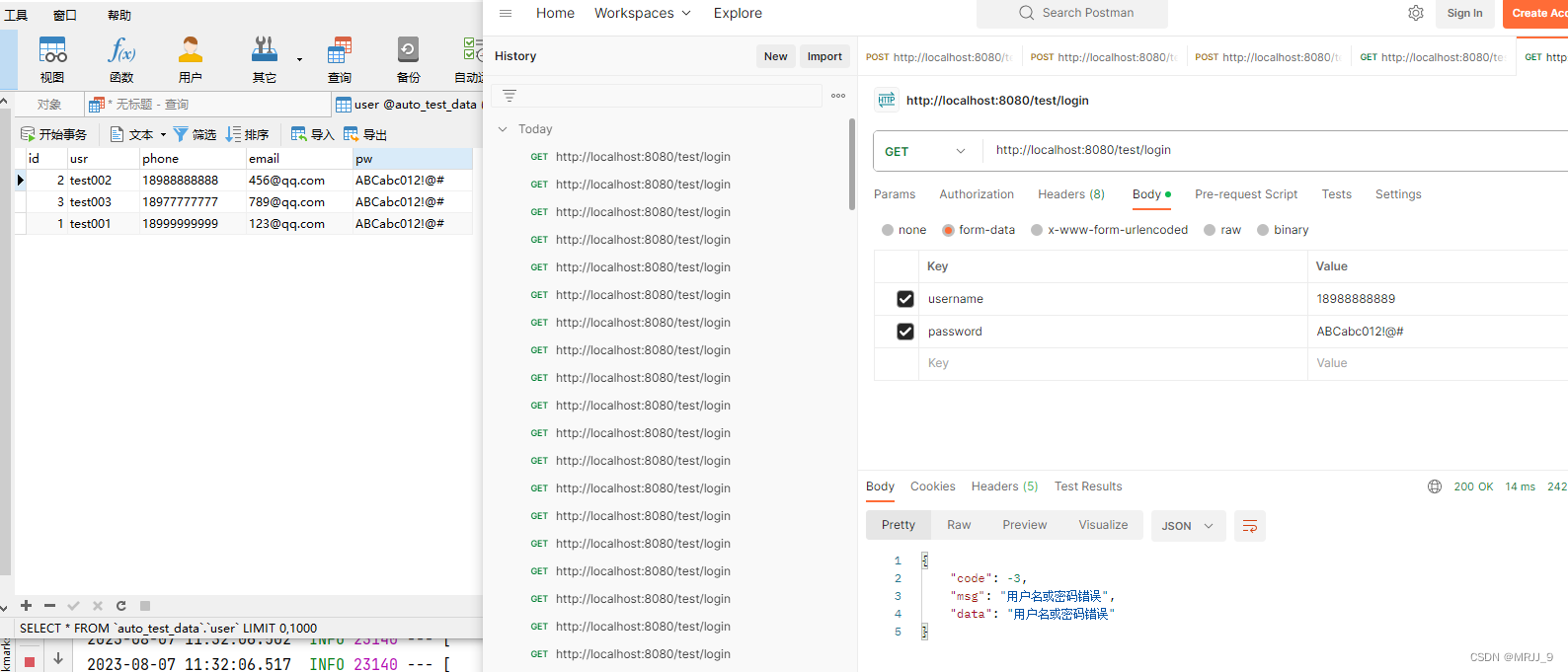
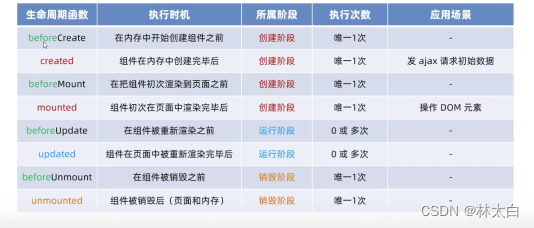
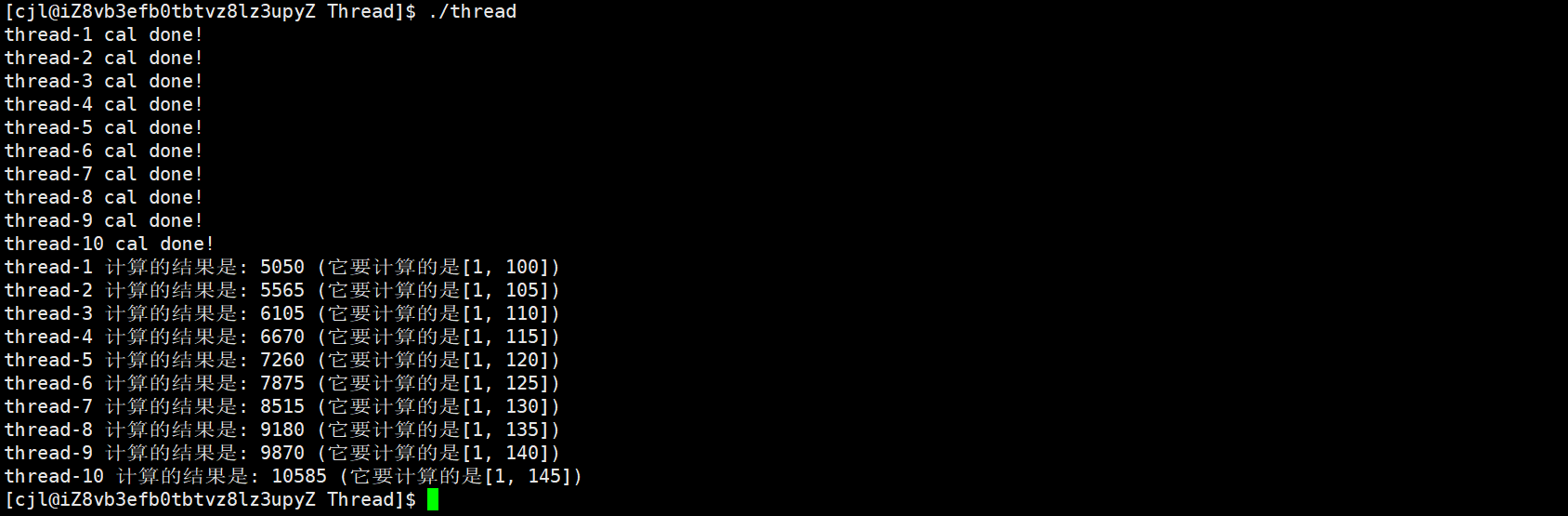
分类任务是对离散变量预测，通过比较分类的概率来判断预测的结果。

softmax回归和线性回归一样也是将输入特征与权重做线性叠加，但是softmax回归的输出值个数等于标签中的类别数，这样就可以用于预测分类问题。

分类问题和线性回归的区别：分类任务通常有多个输出，作为不同类别的置信度。

 

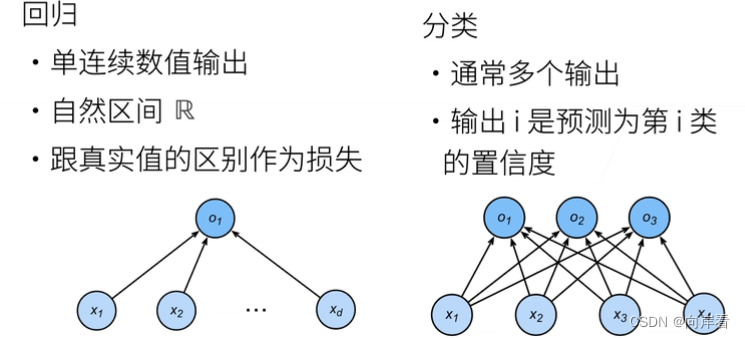
一、softmax回归

1.1 网络架构

为了解决线性模型的分类问题，我们需要和输出一样多的仿射函数，每个输出对应它自己的仿射函数。

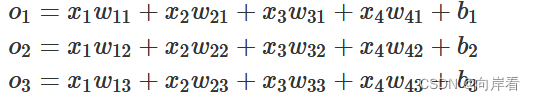
与线性回归一样，softmax回归也是一个单层神经网络。

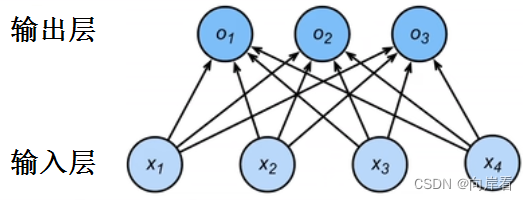
在softmax回归中，输出层的输出值大小就代表其所属类别的置信度大小，置信度最大的那个类别我们将其作为预测。

1.2 softmax运算

首先，分类任务的目标是通过比较每个类别的置信度大小来判断预测的结果。但是，我们不能选择未规范化的最大输出值的 的类别作为我们的预测，原因有两点：

1. 输出值 的总和不一定为1

2. 输出值 有可能为负数。

这违反了概率论基本公理，很难判断所预测的类别是否真符合真实值。

softmax函数通过如下公式，解决了以上问题：

softmax函数确保了输出值的非负，和为1，这一种规范手段。

1.3 交叉熵损失函数

 交叉熵损失常用来衡量两个概率之间的差别。