❓ 剑指 Offer 34. 二叉树中和为某一值的路径

难度：中等

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

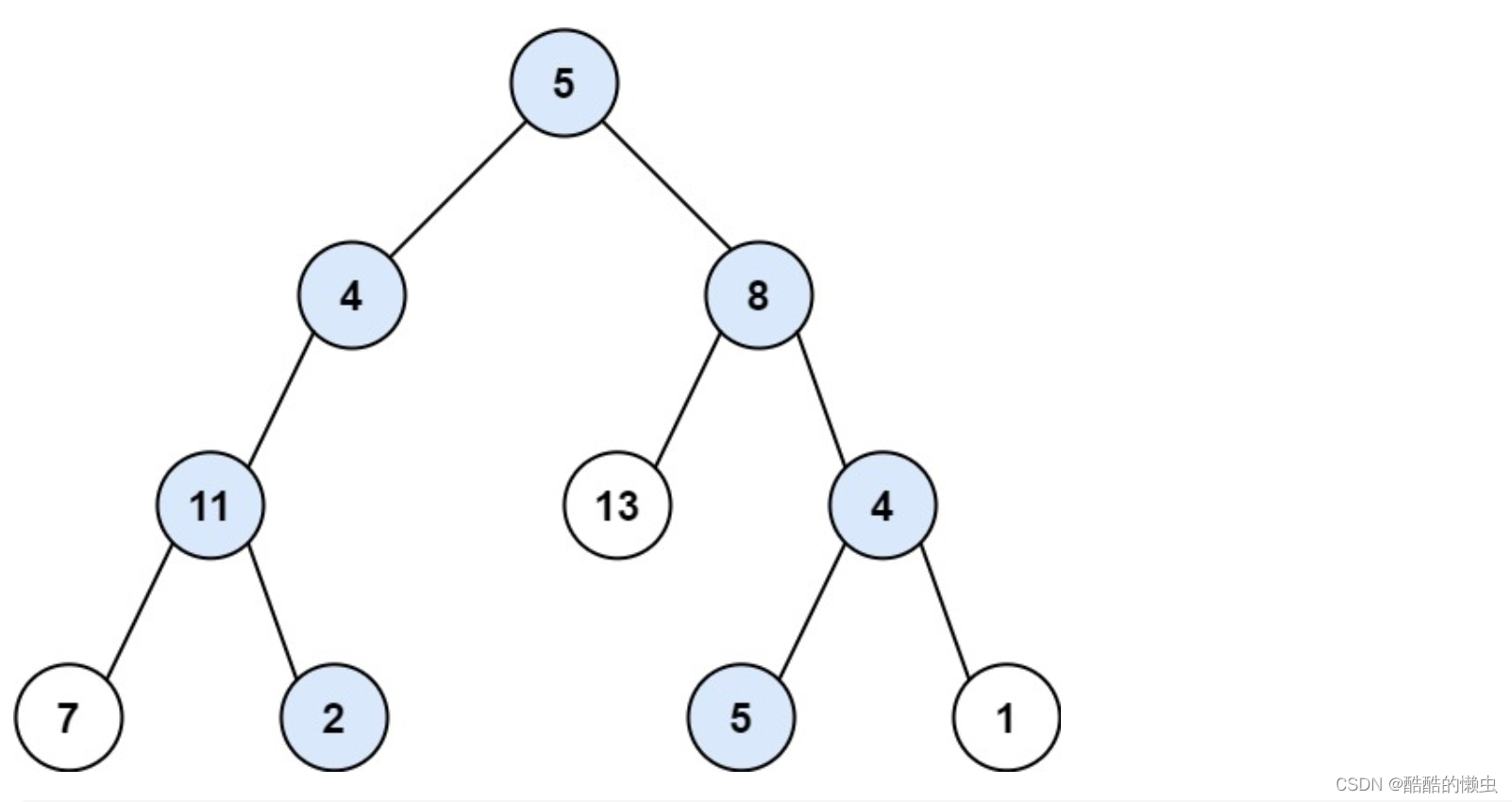
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

• 树中节点总数在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

注意：本题与 113. 路径总和 II 相同。

💡思路：dfs

深度优先搜索的方式，枚举每一条从根节点到叶子节点的路径。

• 当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径，将 数组 tmp 加入 ans。
• 返回时，要删除当前数组 tmp 最后一个元素。

🍁代码：(C++、Java)

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    vector<vector<int>> ans;

    void path(TreeNode* root, vector<int>& tmp, int sum){
        if(root == nullptr) return;
        sum -= root->val;
        tmp.push_back(root->val);
        if(sum == 0 && root->left == nullptr && root->right == nullptr) {
            ans.push_back(tmp);
        }else{
            path(root->left, tmp, sum);
        path(root->right, tmp, sum);
        }
        tmp.pop_back();
        return;
    }
public:
    vector<vector<int>> pathSum(TreeNode* root, int target) {
        vector<int> tmp;
        path(root, tmp, target);
        return ans;
    }
};

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<List<Integer>> ans = new LinkedList<List<Integer>>();
    private void path(TreeNode root, List<Integer> tmp, int sum){
        if(root == null) return;
        sum -= root.val;
        tmp.add(root.val);
        if(sum == 0 && root.left == null && root.right == null) {
            ans.add(new LinkedList(tmp));
        }else{
            path(root.left, tmp, sum);
            path(root.right, tmp, sum);
        }
        tmp.remove(tmp.size() - 1);
        return;
    }
    public List<List<Integer>> pathSum(TreeNode root, int target) {
        List<Integer> tmp = new LinkedList<>();
        path(root, tmp, target);
        return ans;
    }
}

🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：$O(n^2)$，其中 n 为树的节点数。在最坏情况下，树的上半部分为链状，下半部分为完全二叉树，并且从根节点到每一个叶子节点的路径都符合题目要求。此时，路径的数目为 $O(n)$，并且每一条路径的节点个数也为 $O(n)$，因此要将这些路径全部添加进答案中，时间复杂度为$O(n^2)$。
• 空间复杂度：$O(n)$，空间复杂度主要取决于栈空间的开销，栈中的元素个数不会超过树的节点数。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN—力扣专栏，每日更新！

注： 如有不足，欢迎指正！