【笔记】线段树

Start

【笔记】线段树目录

- - 简介
  - 定义
  - 建树
  - 更新
  - 例题1: 单点修改，区间查询
  - - 单点修改
    - 区间查询
    - 本题完整代码
  - 例题2: 区间修改，单点查询
  - - 思路
    - 本题完整代码
  - 例题3: 区间修改，区间查询
  - - 懒标记
    - - 基本思想
      - 应用
    - 区间修改
    - 本题完整代码

简介

线段树是一棵二叉树。如果删去最后一层节点，它是一棵完全二叉树。

线段树是一种常用于处理区间问题的数据结构，分为递归式线段树和非递归式线段树（又称zkw线段树）。

其时间复杂度一般为 $\log n)$ ，不过常数较大。如果追求最优解，建议使用树状数组。

线段树的常用操作共有 $3$ 种，分别是：

单点修改，区间查询。
区间修改，单点查询。
区间修改，区间查询。

下面的例题就以这三种情况和求和操作为例讲解。

定义

放个图：

线段树

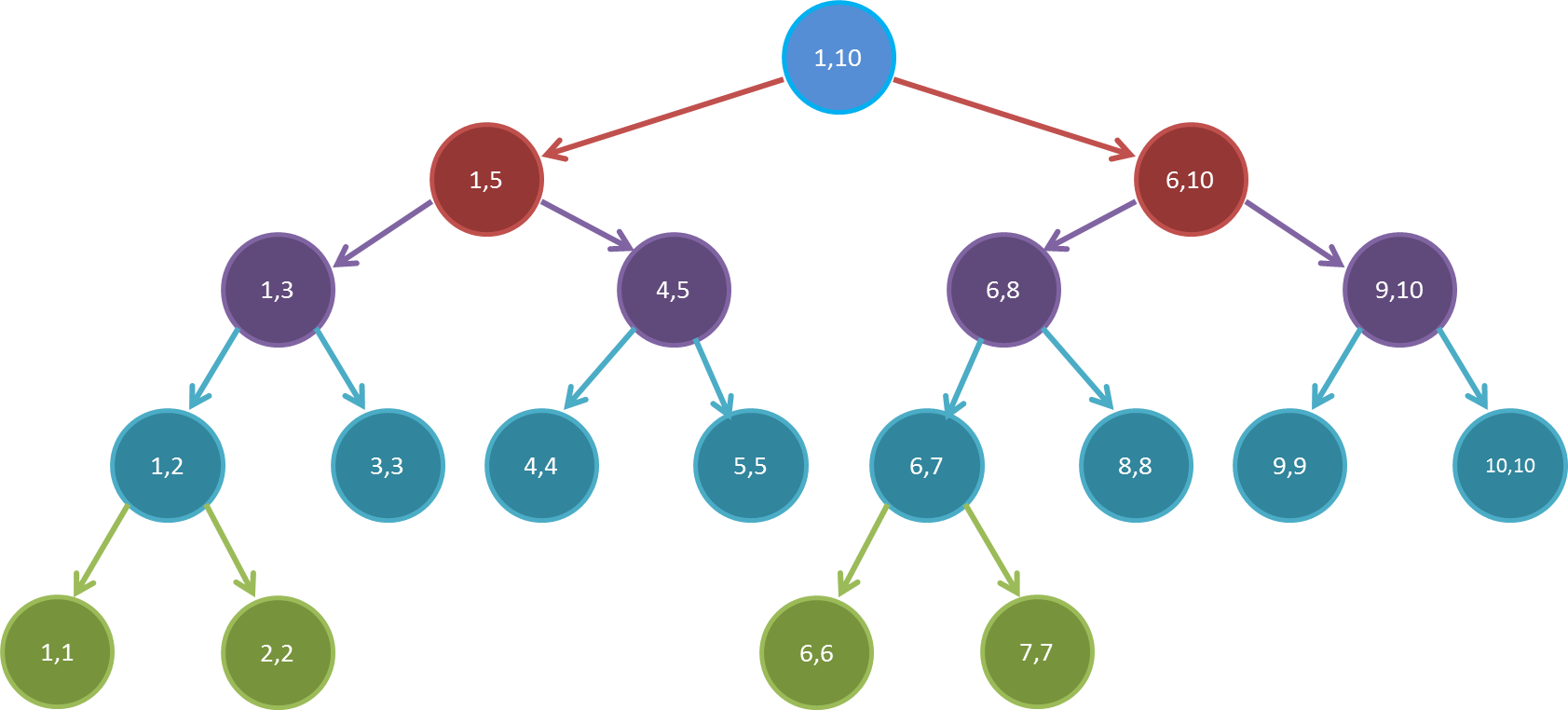
我们考虑完全二叉树的性质：
若当前节点的编号为 $x$ ，则左儿子的编号为 $2 x$ ，右儿子的编号为 $2 x + 1$ 。

由于线段树是完全二叉树，所以线段树的节点编号也遵循这个原则。

但是我们需要频繁用到 $\times2,+1$ 等操作，怎么能让它效率高一点呢？

答案就是“位运算”。 $\times 2$ 可以用 x << 1 替代， $\times 2 + 1$ 可以用 x << 1 | 1 替代。

现在看我们需要维护什么。

对于每个节点，我们分别维护区间左端点 $l$ ，区间右端点 $r$ ，以及维护的区间值 $x$ 和懒标记（如果你有的话）。

节点用结构体数组维护，下标遵循完全二叉树的性质。

上代码：

const int N = 100010;

struct Segment_Tree_Node
{
	int l, r;	// 区间左右端点
	int sum;	// 这里以区间和为例
	int lazy;	// 懒标记，只在有区间修改时用
}tr[N << 2];

有的同学就会问了：为什么要开 $4$ 倍空间呢？

观察我们上面提到的：

线段树是一棵二叉树。如果删去最后一层节点，它是一棵完全二叉树。

假设我们维护的数列长度为 $n$ 。

因为叶子节点的 $l$ 与 $r$ 相等，所以叶子节点个数是 $n$ 。

上面的所有节点共有大约 $n - 1$ 个，因为根据等比数列求和公式，

$2^0 + 2^1 + ··· + 2^{n-1}=2^n-1$

但是，叶子节点的下面可能还有一层节点，而这层节点的个数为 $\times n$ 。

所以保守起见，我们需要开 $\times n = 4 \times n$ 的空间。

建树

所谓建树，就是遍历所有节点，并初始化左右端点和维护的数值。

我们考虑递归遍历。

这个不难，直接放代码：

void build(int u, int l, int r) // 当前区间编号，区间左右端点
{
	if (l == r) tr[u] = {l, r, a[l], 0}; // 初始化叶子节点的左右端点和数值
	else
	{
		tr[u] = {l, r}; // 初始化非叶子节点的左右端点
		LL mid = l + r >> 1; // 以本区间中点向下取整作为左儿子的右端点
		build(u << 1, l, mid); // 建左儿子的树
		build(u << 1 | 1, mid + 1, r); // 建右儿子的树
		pushup(u); // 用子节点的数值更新父节点数值
	}
}

更新

我们发现建树用到了 pushup 操作，这个是用子节点的数值更新父节点数值。

很简单，放代码：

void pushup(LL u)
{
	tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
	// 用左右儿子的sum更新该节点的sum
}

例题1: 单点修改，区间查询

原题链接：P3374 【模板】树状数组 1

~~不要说我用树状数组的题练习线段树，我找不到线段树的模板题才用的这个~~

单点修改

如果递归到这个点所在的叶子节点就直接修改，否则判断它在这个区间的左儿子还是右儿子并递归。

代码：

void modify(int u, int x, int d) // 当前节点编号、修改的节点编号、加的数值
{
    if (tr[u].l == x && tr[u].r == x) // 如果当前的节点和要修改的节点相同就直接修改
        tr[u].sum += d;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1; // 否则取当前区间的中点
        if (x <= mid) modify(u << 1, x, d); // 如果在左儿子就递归到左儿子
        else modify(u << 1 | 1, x, d); // 如果在右儿子就递归到右儿子 
        pushup(u); // 因为修改了，所以更新一下当前节点的值
    }
}

区间查询

结合代码理解：

int query(int u, int l, int r) // 当前节点编号、查询区间的左右端点
{
    if (tr[u].l >= l && tr[u].r <= r) // 如果当前节点完全被查询就返回这个区间的值
        return tr[u].sum;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1; // 否则取当前区间的中点
        int res = 0;
        if (l <= mid) res += query(u << 1, l, r); // 涉及到左儿子
        if (r > mid) res += query(u << 1 | 1, l, r); // 涉及到右儿子
        return res; // 返回
    }
}

本题完整代码

#include <iostream>

using namespace std;

const int N = 500010;

struct Segment_Tree_Node
{
	int l, r;
	int sum;
}tr[N * 4];

int n, m;
int a[N];

void pushup(int u)
{
	tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r)
{
	if (l == r) tr[u] = {l, r, a[l]};
	else
	{
		tr[u] = {l, r};
		int mid = l + r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
		pushup(u);
	}
}

void modify(int u, int x, int d)
{
    if (tr[u].l == x && tr[u].r == x)
        tr[u].sum += d;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, d);
        else modify(u << 1 | 1, x, d);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
        return tr[u].sum;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        int res = 0;
        if (l <= mid) res += query(u << 1, l, r);
        if (r > mid) res += query(u << 1 | 1, l, r);
        return res;
    }
}

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++ )
		scanf("%d", &a[i]);

	build(1, 1, n);

	int op, l, r, d;
	while (m -- )
	{
		scanf("%d%d%d", &op, &l, &r);
		if (op == 1) modify(1, l, r);
		else printf("%d\n", query(1, l, r));
	}

	return 0;
}

例题2: 区间修改，单点查询

原题链接：P3368 【模板】树状数组 2

思路

相信大家都学过差分，它可以 $O (1)$ 的时间复杂度进行区间修改。

所以我们直接把刚才的数组进行差分，再建树。

注意：由于差分涉及在第 $n + 1$ 个节点中进行操作，所以建树时要到 $n + 1$ 。

本题完整代码

#include <iostream>

using namespace std;

const int N = 500010;

struct Segment_Tree_Node
{
	int l, r;
	int sum;
}tr[N * 4];

int n, m;
int a[N], b[N];

void pushup(int u)
{
	tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r)
{
	if (l == r) tr[u] = {l, r, b[l]};
	else
	{
		tr[u] = {l, r};
		int mid = l + r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
		pushup(u);
	}
}

void modify(int u, int x, int d)
{
    if (tr[u].l == x && tr[u].r == x)
        tr[u].sum += d;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, d);
        else modify(u << 1 | 1, x, d);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
        return tr[u].sum;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        int res = 0;
        if (l <= mid) res += query(u << 1, l, r);
        if (r > mid) res += query(u << 1 | 1, l, r);
        return res;
    }
}

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++ )
		scanf("%d", &a[i]), b[i] = a[i] - a[i - 1]; // 差分

	build(1, 1, n + 1); // 建树到 n + 1

	int op, l, r, d;
	while (m -- )
	{
		scanf("%d%d", &op, &l);
		if (op == 1)
		{
		    scanf("%d%d", &r, &d);
		    modify(1, l, d), modify(1, r + 1, -d); // 区间修改时修改区间的端点
		}
		else printf("%d\n", query(1, 1, l)); // 查询当前节点的前缀和
	}

	return 0;
}

例题3: 区间修改，区间查询

原题链接：P3372 【模板】线段树 1

懒标记

基本思想

当进行区间修改时，只修改当前区间，而它的子节点的修改先欠着，等用到了子节点的时候再往下传。

应用

将懒标记下传的操作：pushdown 函数

如果这个节点有懒标记，就把懒标记加到子节点的懒标记中，并把当前节点的懒标记清空。

代码：

void pushdown(LL u)
{
	Segment_Tree_Node &U = tr[u], &L = tr[u << 1], &R = tr[u << 1 | 1];
	if (tr[u].lazy) // 如果当前节点有懒标记
	{
		L.lazy += U.lazy, L.sum += (L.r - L.l + 1) * U.lazy; // 左儿子懒标记和区间和
		R.lazy += U.lazy, R.sum += (R.r - R.l + 1) * U.lazy; // 右儿子懒标记和区间和
		U.lazy = 0; // 清空当前节点懒标记
		// 显然，区间和在加的时候应该加上懒标记和区间长度的乘积
	}
}

区间修改

这里和 pushdown 差不多，修改懒标记和区间和。

代码：

void modify(LL u, LL l, LL r, LL d)
{
	if (tr[u].l >= l && tr[u].r <= r) // 如果这个区间被完全包含
	{
		tr[u].lazy += d; // 修改懒标记 
		tr[u].sum += (tr[u].r - tr[u].l + 1) * d; // 区间和 + d * 区间长度
	}
	else
	{
		pushdown(u);
		LL mid = tr[u].l + tr[u].r >> 1;
		if (l <= mid) modify(u << 1, l, r, d);
		if (r > mid) modify(u << 1 | 1, l, r, d);
		pushup(u);
	}
}

本题完整代码

#include <iostream>

using namespace std;

typedef long long LL;

const LL N = 100010;

struct S_Tree
{
	LL l, r;
	LL sum, lazy;
}tr[N * 4];

LL n, m;
LL a[N];

void pushup(LL u)
{
	tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void pushdown(LL u)
{
	S_Tree &U = tr[u], &L = tr[u << 1], &R = tr[u << 1 | 1];
	if (tr[u].lazy)
	{
		L.lazy += U.lazy, L.sum += (L.r - L.l + 1) * U.lazy;
		R.lazy += U.lazy, R.sum += (R.r - R.l + 1) * U.lazy;
		U.lazy = 0;
	}
}

void build(LL u, LL l, LL r)
{
	if (l == r) tr[u] = {l, r, a[l], 0};
	else
	{
		tr[u] = {l, r};
		LL mid = l + r >> 1;
		build(u << 1, l, mid);
		build(u << 1 | 1, mid + 1, r);
		pushup(u);
	}
}

void modify(LL u, LL l, LL r, LL d)
{
	if (tr[u].l >= l && tr[u].r <= r)
	{
		tr[u].lazy += d;
		tr[u].sum += (tr[u].r - tr[u].l + 1) * d;
	}
	else
	{
		pushdown(u);
		LL mid = tr[u].l + tr[u].r >> 1;
		if (l <= mid) modify(u << 1, l, r, d);
		if (r > mid) modify(u << 1 | 1, l, r, d);
		pushup(u);
	}
}

LL query(LL u, LL l, LL r)
{
	if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
	else
	{
		pushdown(u);
		LL mid = tr[u].l + tr[u].r >> 1;
		LL res = 0;
		if (l <= mid) res += query(u << 1, l, r);
		if (r > mid) res += query(u << 1 | 1, l, r);
		return res;
	}
}

int main()
{
	scanf("%lld%lld", &n, &m);
	for (LL i = 1; i <= n; i ++ )
		scanf("%lld", &a[i]);

	build(1, 1, n);

	LL op, l, r, d;
	while (m -- )
	{
		scanf("%lld%lld%lld", &op, &l, &r);
		if (op == 1)
		{
			scanf("%lld", &d);
			modify(1, l, r, d);
		}
		else
		{
			LL t = query(1, l, r);
			printf("%lld\n", t);
		}
	}

	return 0;
}