Scikit-learn聚类方法代码批注及相关练习

news2024/9/29 15:26:40

一、代码批注

代码来自：https://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html#sphx-glr-auto-examples-cluster-plot-dbscan-py

import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler

# make_blobs:为聚类产生数据集及其相应的标签；n_samples：样本点个数；centers：类别数；cluster_std：每个类别的方差；random_state：随机种子
# 这里centers里的三个二维坐标，其实代表了聚类的三个中心
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4, random_state=0)

# 标准化
X = StandardScaler().fit_transform(X)

# 预估器，并得出模型（eps：数据点的邻域半径；min_samples：某个数据点的邻域内最少有的数据点个数）
db = DBSCAN(eps=0.2, min_samples=7).fit(X)

# 生成n_samples个False
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
# 预测出的结果（有结果的为True，为噪音的是False）
core_samples_mask[db.core_sample_indices_] = True
# 获得预测结果
labels = db.labels_
# 获得预测的聚类数，忽略掉噪音
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
# 获得噪音数
n_noise_ = list(labels).count(-1)

# 预测出的集群数，对应图中5中颜色
print('Estimated number of clusters: %d' % n_clusters_)
# 预测出噪音点的数量，对应图中的黑点
print('Estimated number of noise points: %d' % n_noise_)
# 同质性：簇的纯洁程度—对比分类问题的精度
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
# 完整性：簇的完整性—对比分类问题的召回率
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
# v测度：用来评估同一个数据集上两个独立赋值的一致性
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
# 调节的兰德系数（ARI）：衡量两个数据分布的吻合程度
print("Adjusted Rand Index: %0.3f" % metrics.adjusted_rand_score(labels_true, labels))
# 调整互信息（AMI）：衡量两个数据分布的吻合程度
print("Adjusted Mutual Information: %0.3f" % metrics.adjusted_mutual_info_score(labels_true, labels))
# 轮廓系数：将某个对象与自己的簇的相似程度和与其他簇的相似程度进行比较（肘方法）
print("Silhouette Coefficient: %0.3f" % metrics.silhouette_score(X, labels))


import matplotlib.pyplot as plt

unique_labels = set(labels)
# 给每个label赋个颜色
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
    # 给噪音为黑色
    if k == -1:
        col = [0, 0, 0, 1]

    # 开始绘制，获得该种类的点
    class_member_mask = (labels == k)
    # core_samples_mask里false就是黑色噪音点
    # 取出同一类的点（这样&可以过滤掉黑点。如果没有core_samples_mask（黑点为false）会把黑点也画很大）
    xy = X[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col), markeredgecolor='k', markersize=14)
    # 获得噪音点，注意：db.core_sample_indices_没出现的的不一定就是噪音点（小圆圈）
    xy = X[class_member_mask & ~core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col), markeredgecolor='k', markersize=6)

plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

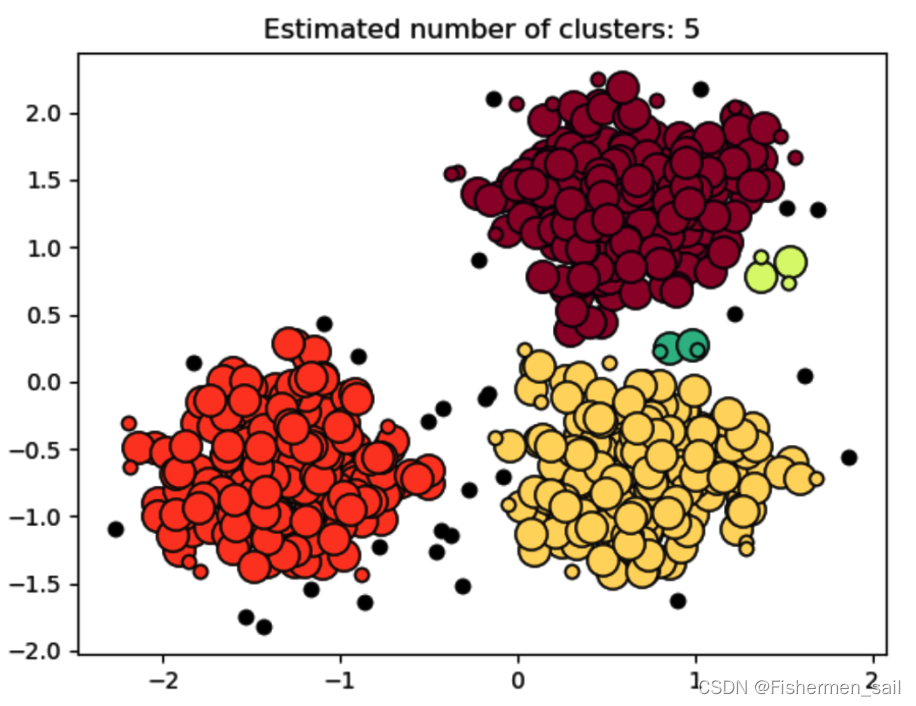
在这里插入图片描述
在实验中一直有个困惑，不知道这个小圆圈是怎么画上去的。它的原因是在“db.core_sample_indices_”和“db.labels”，起初我以为“db.core_sample_indices_”会生成除噪音点以外的其他index，也就是区分开了噪音点与聚类点。但其实并不是，有少部分不在“db.core_sample_indices_”中的点也是聚类点，在下方打印出来的值分别与它俩相对，可以看见前者并没有为32的index，理论上它应该为-1噪音点，但打印出“db.labels”发现index为32的值是1，是一个聚类点。这点也在scikit learn文档最后一段进行了说明，文档解释到图中大的圆为“core sample”，而小的圆为“non-core sample”，它也是聚类的一部分。
在这里插入图片描述

二、DBSCAN的使用

通过改变DBSCAN中min_samples参数观察图形的聚类效果。
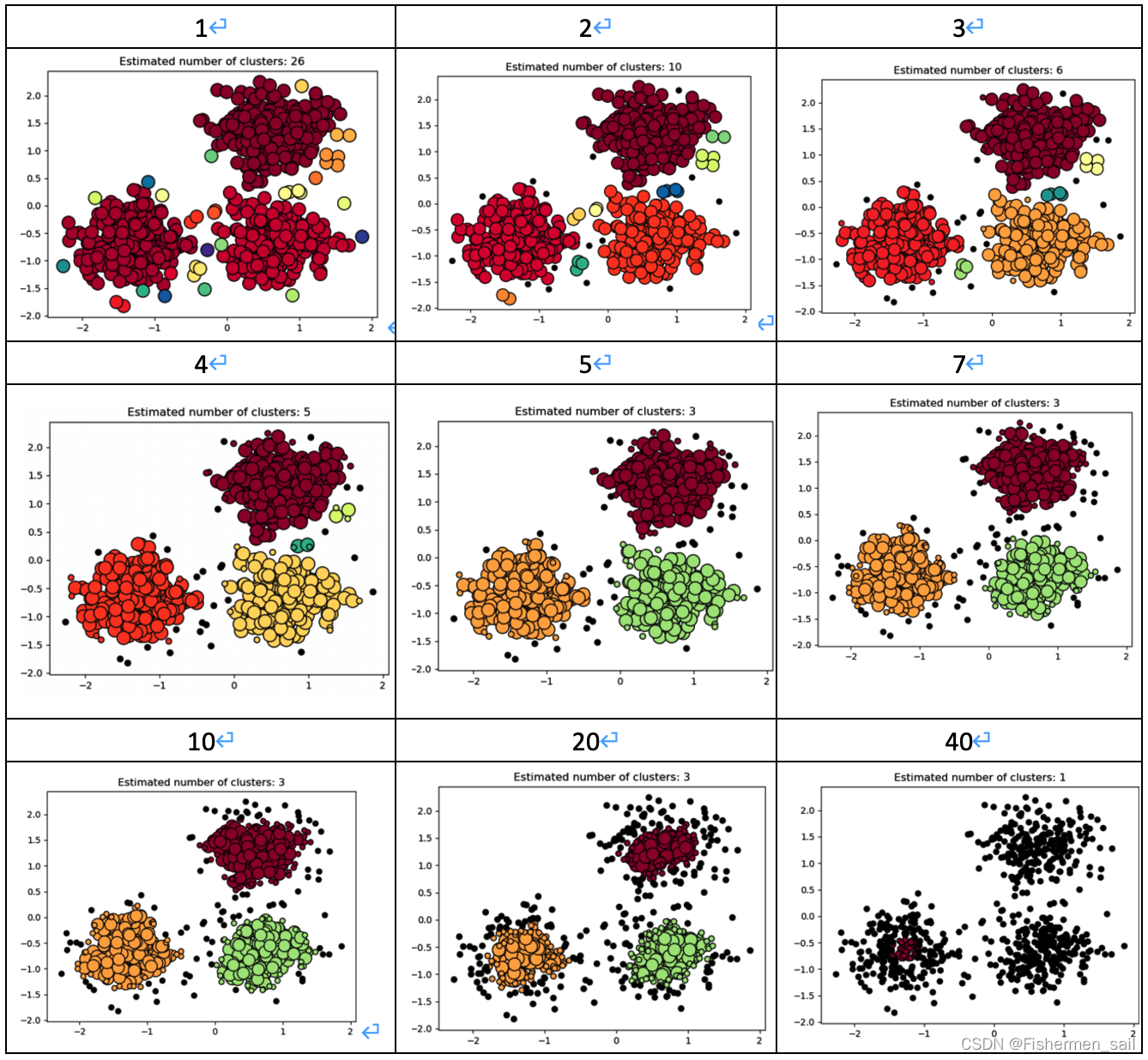
在这里插入图片描述
当min_samples为41时编译器报错。

观察上图可以发现随着min_samples的增大cluster越来越少，噪音点越来越多，直至报错。这是因为DBSCAN算法是基于密度的算法，所以它将密集区域内的点看作核心点（核心样本）。它主要有两个参数：min_samples和eps。

eps表示数据点的邻域半径，如果某个数据点的邻域内至少有min_sample个数据点，则将该数据点看作为核心点。如果某个核心点的邻域内有其他核心点，则将它们看作属于同一个簇。如果min_sampLes设置地太大，那么意味着更少的点会成为核心点，而更多的点将被标记为噪声。

如果将eps设置得非常小，则有可能没有点成为核心点，并且可能导致所有点都被标记为噪声。如下图为eps=0.05，min_samples=5的图。
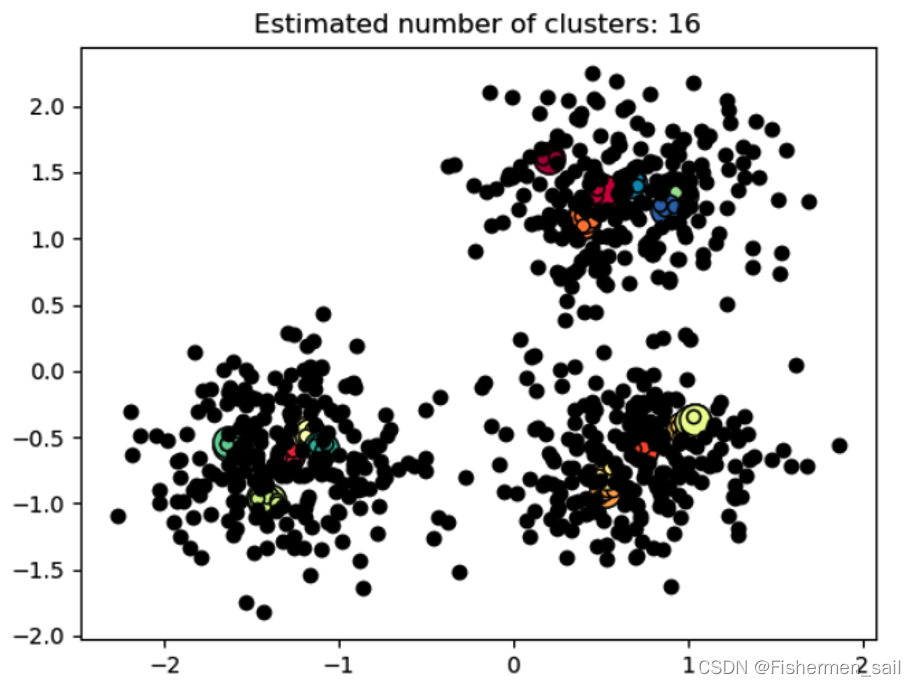
在这里插入图片描述
如果将eps设置为非常大，则将导致所有点都被划分到同一个簇。如下图为esp=0.3，min_samples=5的图。

三、KMeans的使用

由于KMeans并没有“core_sample_indices”这个属性，也就是不会分离出噪音点，需将该条语句注释掉。在画图时，由于并没有噪音点，也要进行相应改写。
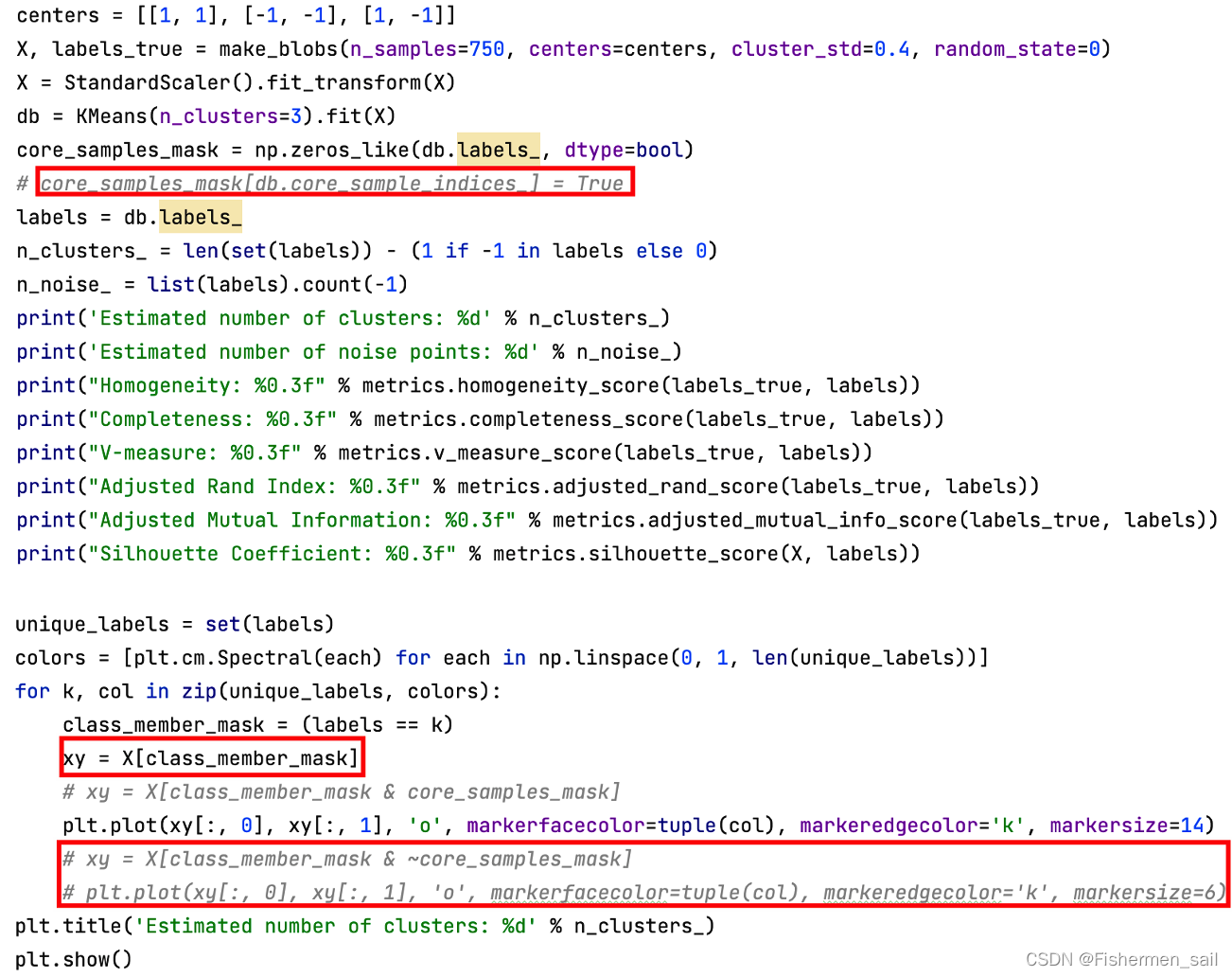
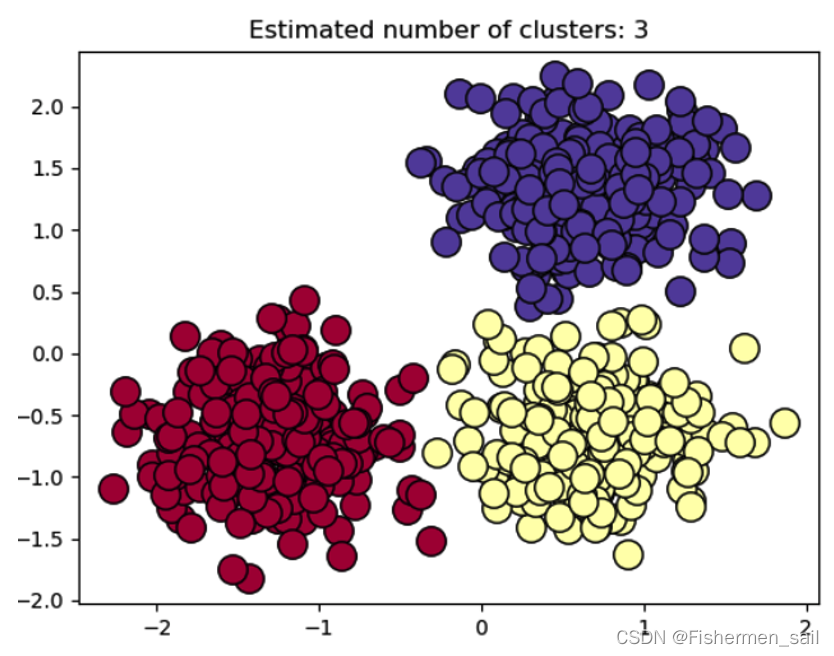
在这里插入图片描述

KMeans算法是根据给定的n个数据对象的数据集，构建n个划分聚类的方法，每个划分聚类即为一个簇。该方法将数据划分为n个簇，每个簇至少有一个数据对象，每个数据对象必须属于而且只能属于一个簇。同时要满足同一簇中的数据对象相似度高，不同簇中的数据对象相似度较小。聚类相似度是利用各簇中对象的均值来进行计算的。

KMeans 算法的处理流程如下，首先，随机地选择k个数据对象，每个数据对象代表一个簇中心，即选择k个初始中心；对剩余的每个对象，根据其与各簇中心的相似度（距离），将它赋给与其最相似的簇中心对应的簇；然后重新计算每个簇中所有对象的平均值，作为新的簇中心。不断重复以上这个过程，直到准则函数收敛，也就是簇中心不发生明显的变化。通常采用均方差作为准则函数，即最小化每个点到最近簇中心的距离的平方和。新的簇中心计算方法是计算该簇中所有对象的平均值，也就是分别对所有对象的各个维度的值求平均值，从而得到簇的中心点。

四、KMeans与DBSCAN对比

KMeans	DBSCAN
使用簇的基于原型的概念。	使用基于密度的概念。
只能用于具有明确定义的质心（如均值）的数据。	要求密度定义（基于传统的欧几里得密度概念）对于数据是有意义的。
需要指定簇的个数作为参数。	不需要事先知道要形成的簇类的数量，自动确定簇个数。
很难处理非球形的簇和不同形状的簇。	可以发现任意形状的簇类，可以处理不同大小和不同形状的簇。
可以用于稀疏的高纬数据，如文档数据。	不能很好反映高维数据。
可以发现不是明显分离的簇，即便簇有重叠也可以发现。	会合并有重叠的簇。