Encryption: Computational security 1-4
主讲人:李增鹏(山东大学)
参考教材:Jonathan Katz, Yehuda Lindell, Introduction to Modern Cryptography - Principles and Protocols.
什么是加密
首先,加密方案的目的在于在Alice和Bob之间完成安全的通信。具体地,任意给定明文 m m m,Alice对它进行加密得到 c c c并且通过不安全信道发送给Bob,Bob对 c c c进行解密后得到 m m m,而第三者Eve不能获得 m m m的任何相关信息。
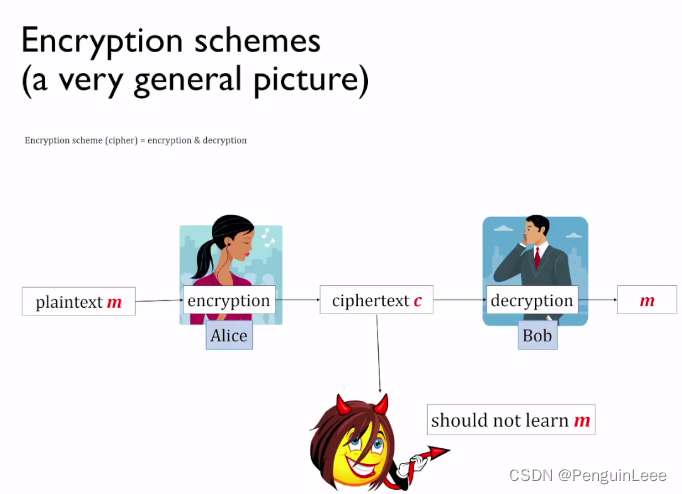
为了做到这个事情,从古至今有很多所谓的密码方案,比如凯撒密码、弗吉尼亚密码、栅栏加密、Enigma机等等。
这些方案的共同特点之一是,没有严谨的理论来确保它们是安全的。与其说是密码科学,不如说是承载了古人灿烂想象力的密码艺术。
这些方案的共同特点之二是,它们都被破掉了。据(Prof. 丁津泰)说,阿根廷人在马岛海战中还在用类似Enigma机的密码系统,于是战场信息理所应当地对英国人单向透明。
可证明安全是密码学从艺术向科学迈出的重要一步。
设计现代密码系统的另一个原则是,密码系统的安全性不依赖于加密方案或者算法的保密,而是依赖于密钥的安全性(Kerckhoffs原则, 1883)。

理由如下:
- 保护密钥其实比保护算法更容易;
- 更换密钥也比更换算法更容易;
- 加密算法进行统一,方便了应用;
- 公开算法,有助于算法漏洞的分析。
于是我们可以根据Kerckhoffs原则把加密系统的general picture进行改写:
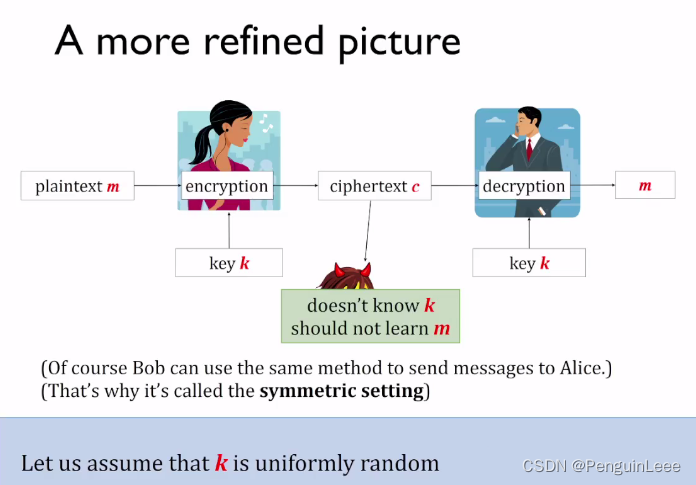
- m m m是明文消息
- 密钥 k k k从均匀分布中抽取
- c = E n c k ( m ) c = Enc_k(m) c=Enck(m)暴露给攻击者
注意到,和加密系统的最一般情况相比,这里我们引入了密钥 k k k,希望攻击者没法获取到 k k k和 m m m的相关信息。
完美的安全性
一些记号:

现在的问题是,在Kerckhoffs原则的框架下,我们怎么去定义一个密码系统的安全性?
想法一:
定义. 如果攻击者没办法计算 k k k,那么这个scheme就是安全的。
——密钥不让人知道是确实有道理…吧。
一个反例就是, E n c k ( m ) = m Enc_k(m) = m Enck(m)=m。这种情况下,你确实没暴露任何的 k k k的信息,但是 m m m在裸奔,加密的安全性效果类似于皇帝的新衣。

想法二:
定义. 如果攻击者没办法计算 m m m,那么这个scheme就是安全的。
如果一个攻击者只需要计算密文 m m m的某些特征就能推断出足够的信息,那这个scheme还安全吗?
比如我猜一个四字地名是齐齐哈尔还是乌鲁木齐。我甚至只需要这四个字里带几个齐字或者有没有重复字就能推测出答案。
想法三:
定义. 如果攻击者不能获得 m m m的任何相关信息,那么这个scheme就是安全的。
但是攻击者可能已经获得了一些先验信息,比如知道消息 m m m是用英语写的。
想法四:
定义. 如果攻击者不能获得 m m m的任何额外信息,那么这个scheme就是安全的。
这个是比较靠谱的,但是怎么正式表述它?
一个例子是使用概率分布/信息论进行描述:
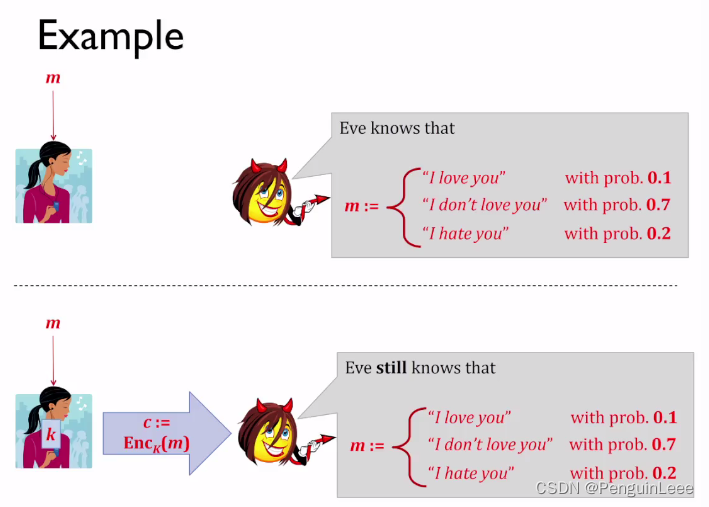
上半拉图是通信前。 m m m在Alice手里,攻击者什么都不知道,它有关于 m m m的一个先验分布。
下半拉图是通信后。 m m m在Alice手里,攻击者知道 c = E n c k ( m ) c = Enc_k(m) c=Enck(m),在知道 c c c的前提下,攻击者的先验没有产生丝毫的变化。这就是所谓的“攻击者不能获得关于 m m m的任何额外信息”。
于是,我们得到基于条件概率表述的完美安全性定义:

等价地,我们有几个定义:
- 明文 m m m的分布和 E n c k ( m ) Enc_k(m) Enck(m)是独立的。
- E n c k ( m ) Enc_k(m) Enck(m)的分布和 m m m无关。
- 对任意的 m 0 m_0 m0、 m 1 m_1 m1,我们有 E n c k ( m 0 ) Enc_k(m_0) Enck(m0)、 E n c k ( m 1 ) Enc_k(m_1) Enck(m1)有相同的分布。
完美安全性的一个等价定义是对手的不可识别性(Adversarial Indistinguishability)。这里,我们引入一个对手 A \mathcal{A} A,并且定义什么是 A \mathcal{A} A的不可识别性(粗略地说,给定明文 m 0 , m 1 m_0, m_1 m0,m1并且随机挑选一个进行加密得到 c c c, A \mathcal{A} A没法知道这个 c c c对应的明文是 m 0 , m 1 m_0, m_1 m0,m1的哪个)。
为了定义完美安全性,我们引入一个不可区分性实验(experiment)或者说是游戏(game),记为 P r i v K A , Π e a v PrivK^{eav}_{\mathcal A, \Pi} PrivKA,Πeav。这里, Π = ( G e n , E n c , D e c ) \Pi=(Gen, Enc, Dec) Π=(Gen,Enc,Dec)是密码系统,这个游戏只考虑窃听(eavesdropping)攻击者 A \mathcal A A,攻击者拥有的后验信息只有一个 c c c并且试图基于这个 c c c确定明文的一些信息。
定义. P r i v K A , Π e a v PrivK^{eav}_{\mathcal A, \Pi} PrivKA,Πeav定义如下:
- 初始化加密方案(比如,生成密钥 k k k)。
- 攻击者给出一对明文 m 0 , m 1 ∈ M m_0, m_1 \in \mathcal M m0,m1∈M。
- 通信方在攻击者不知情的情况下随机挑选一个 m b , b ∈ { 0 , 1 } m_b, b\in \{0, 1\} mb,b∈{0,1},加密后返回 c c c。
- 攻击者根据 c c c给出一个 b b b的估计 b ′ b' b′。注意,这个 b ′ b' b′可能是一个概率分布。
- 如果 b = b ′ b = b' b=b′,那么攻击者赢(return 1),反之输(return 0)。
如果系统是安全的,那么你攻击者对 c c c再怎么折腾,最后输出的结果和瞎猜的效果是一样的。
于是我们可以定义不可区分性:
定义. 定义在明文空间 M \mathcal M M上的密码系统 ( G e n , E n c , D e c ) (Gen, Enc, Dec) (Gen,Enc,Dec)是不可区分的,如果:
P [ P r i v K A , Π e a v = 1 ] = 1 2 P[PrivK^{eav}_{\mathcal A, \Pi} = 1] = \frac{1}{2} P[PrivKA,Πeav=1]=21
一次性密码本
现实中就存在一个具有完美安全性的加密方案:一次性密码本(One Time Pad, OTP)。
对于一个二进制串 m m m,我们随机生成和 m m m等长的二进制串 k k k,其中 k k k的每一位都是独立的均匀分布, c = E n c k ( m ) = m ⊕ k c = Enc_k(m) = m \oplus k c=Enck(m)=m⊕k,其中 ⊕ \oplus ⊕被定义为异或运算。
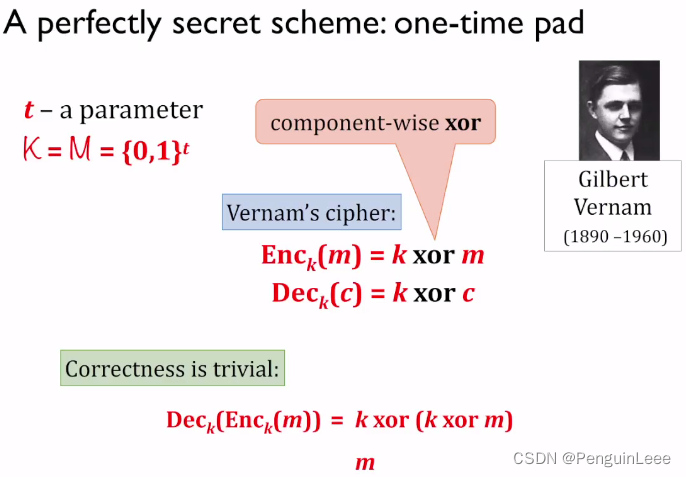
OTP的安全性是显然的。因为,对每个 m m m而言, c c c的每一位都是均匀分布的。

我们将OTP进行一般化:
( G , + ) (G, +) (G,+)为加群。 K = M = C = G \mathcal K = \mathcal M=\mathcal C=G K=M=C=G。于是,
- E n c k ( m ) = m + k Enc_k(m) = m+k Enck(m)=m+k
-
D
e
c
k
(
m
)
=
m
−
k
Dec_k(m)=m-k
Deck(m)=m−k
构成了一次性密码本。
但是OTP不实用,因为:
-
密钥和明文等长
-
一次一密,用后即焚,否则可能会泄露信息。
比如在OTP中,如果相同的密钥加密 m 1 , m 2 m_1, m_2 m1,m2后得到 c 1 , c 2 c_1, c_2 c1,c2,那么攻击者就知道 m 1 ⊕ m 2 = c 1 ⊕ c 2 m_1 \oplus m_2 = c_1 \oplus c_2 m1⊕m2=c1⊕c2——这泄露了明文的信息。

此外,我们可以证明,一个密码系统如果是具有完美安全性的,那么必然是 ∣ K ∣ ≥ ∣ M ∣ |\mathcal K| \geq |\mathcal M| ∣K∣≥∣M∣。
(原因很简单,假如 ∣ K ∣ < ∣ M ∣ |\mathcal K| < |\mathcal M| ∣K∣<∣M∣,原本攻击者是要去猜 m m m的,现在攻击者猜 k k k的胜算还比猜 m m m的胜算还大,这意味着加密过程泄露了信息。)
于是,OTP就成了完美安全性中最高效的方案。

“可以收手了吗,阿祖?”
限制攻击者的能力:不可区分性、语义安全性

要想做出实用性更强的密码系统,一个想法是对攻击者的能力进行限制。
限制方法包括:
- 限制攻击者的计算能力——计算安全性。
- 其他方法:量子密码学、内存限制模型etc
量子密码学的特征是:攻击者(Eve)不可能在通信方(Alice和Bob)不知情的情况下实现窃听。一旦攻击者成功实施窃听,那么量子的状态就会被干扰,通信方可以通过基于量子状态传输的通信内容知道自己被窃听了。


(需要注意一点,量子密码和量子计算不是一个东西)
主流方法是对攻击者进行计算能力的限制。如果攻击者可以不计成本地做穷举攻击,那么什么样的密码都会被破解。

问题来了:如何定义对攻击者计算能力的限制?
攻击者可以买若干块V100并且用到报废、或者一年内租若干台云服务器吗?
即使有这些个计算资源,那攻击者运行什么样的攻击算法呢?
所以说这种定义在理论上不是太美观的,也不方便分析。

下面我们对计算模型进行抽象。具体地,我们可以用图灵机描述攻击者的能力:

一个系统 X X X是 ( t , ϵ ) (t, \epsilon) (t,ϵ)安全的,如果任意一个运行时长不超过 t t t的图灵机破解它的概率不超过 ϵ \epsilon ϵ。
其实存在很多图灵机模型,基本上都可以证明它们和最一般的图灵机是等价的。然后Church-Turing命题也告诉我们,任何在算法上可计算的问题同样可由图灵机计算。于是我们可以把各种各样基于图灵机的模型抽象一下变成一个个算法,于是所有的讨论都基于算法进行,这就避免了去脑补图灵机的纸带和读写头怎么飞舞。
对于前述的 ( t , ϵ ) (t, \epsilon) (t,ϵ)安全性,我们使用渐进分析的方法进行具体化。
- 图灵机运行 t t t步,意味着“高效的计算”
- ϵ \epsilon ϵ,是一个非常小(接近0)的数
定义这些东西的方式是使用渐进分析的思路。
直接说结论,我们认为的小是小于任何的多项式倒数,即小于任何的 1 / p o l y ( n ) 1/poly(n) 1/poly(n)。
我们认为的高效计算是有多项式复杂度的计算。


这种用多项式定义的小具有比较好的性质:

基于上面的东西,我们对计算安全性进行进一步的定义。首先,我们对密钥加密方案(private-key encryption scheme)进行定义:
定义. 私钥密码学方案是三个概率多项式时间(Probability polynomial time, PPT)算法 ( G e n , E n c , D e c ) (Gen, Enc, Dec) (Gen,Enc,Dec),其中:
- G e n Gen Gen:输入安全参数 n n n返回一个密钥 k k k。一般认为 ∣ k ∣ ≥ n |k| \geq n ∣k∣≥n。
- E n c Enc Enc:输入密钥 k k k和明文消息 m ∈ { 0 , 1 } ∗ = ⋃ N = 1 ∞ { 0 , 1 } N m \in \{0, 1\}^* = \bigcup_{N=1}^\infty \{0, 1\}^N m∈{0,1}∗=⋃N=1∞{0,1}N。输出的密文有可能是随机的。
- D e c Dec Dec:输入密钥 k k k和密文消息 c c c,输出 m m m或者抛出错误。
要求:对于任意的 n , k , m n, k, m n,k,m, D e c k ( E n c k ( m ) ) = m Dec_k(Enc_k(m)) = m Deck(Enck(m))=m。
我们仍然没有很好地假设攻击者的能力。比如攻击者可能用什么样的算法进行攻击。我们接下来设计的安全性定义将防御住攻击者在给定计算能力的情况下的任何攻击。
在完美安全性中,攻击者不能从密文中获取任何明文的相关信息。在限制了攻击者的计算能力后,我们将定义语义安全性。语义安全性不是那么实用,我们又搞出了一个叫不可区分性的东西。不可区分性和语义安全性等价,但是不可区分性好用。
我们在攻击者能力受限的情况下,也搞一个不可识别性之类的东西。和完美安全性那里引入的game的区别在于,我们改动两个地方:
- 攻击者的能力被限制为多项式时间
- 攻击者攻击的成功率是小的,这个小被定义为 1 2 + ϵ ( n ) \frac{1}{2}+ \epsilon(n) 21+ϵ(n)
于是我们得到game:
定义. adversarial indistinguishability窃听攻击下的不可区分性实验 P r i v K A , Π e a v ( n ) PrivK^{eav}_{\mathcal A, \Pi}(n) PrivKA,Πeav(n):
- 攻击者 A \mathcal A A给定安全参数,输出两个密文 m 0 , m 1 m_0, m_1 m0,m1,其中 ∣ m 0 ∣ = ∣ m 1 ∣ |m_0| = |m_1| ∣m0∣=∣m1∣
- 防御方生成密钥 k k k和一个随机比特 b b b。计算 c = E n c k ( m b ) c = Enc_k(m_b) c=Enck(mb)
- 攻击者获得 c c c后通过一通计算输出比特 b ′ b' b′
- 如果 b ′ = b b' = b b′=b,则攻击者赢,记为 P r i v K A , Π e a v ( n ) = 1 PrivK^{eav}_{\mathcal A, \Pi}(n) = 1 PrivKA,Πeav(n)=1
基于此我们有计算不可区分性的定义:
定义. 加密方案
Π
=
(
G
e
n
,
E
n
c
,
D
e
c
)
\Pi = (Gen, Enc, Dec)
Π=(Gen,Enc,Dec)在窃听攻击下是计算不可区分的(EAV-SECURE),如果对所有的PPT算法攻击
A
\mathcal A
A,都存在足够小的函数,使得对于任意的
n
n
n,
P
[
P
r
i
v
K
A
,
Π
e
a
v
(
n
)
=
1
]
≤
1
2
+
ϵ
(
n
)
P[PrivK^{eav}_{\mathcal A, \Pi}(n) = 1] \leq \frac{1}{2} + \epsilon(n)
P[PrivKA,Πeav(n)=1]≤21+ϵ(n)
其中 ϵ ( n ) \epsilon(n) ϵ(n)是我们前面定义的小量。
一个等价的定义是,假设我们给实验 P r i v K A , Π e a v ( n ) PrivK^{eav}_{\mathcal A, \Pi}(n) PrivKA,Πeav(n)开了影分身,这两个影分身实验在选择比特 b b b的时候一个选了0一个选了1,那么攻击者其实是分辨不出他自己在和哪个影分身搏斗的。
这个定义的书写留作练习,或者参考书。
注意,这里涉及的加密方案并不需要隐藏明文的长度信息。我们暂时假设明文长度都是相等的,具体为什么要这么假设不妨参考书中的相关内容,因为这个问题暂时不影响主线叙述。
为了介绍语义安全性,我们首先更进一步地品味计算不可区分性的意义。
-
计算不可区分,意味着攻击者不可能通过他的那些计算花招在猜测明文的某一个比特方面有显著的优势。
-
计算不可区分,意味着攻击者不可能通过他的那些计算花招学到明文的任意一个函数 f ( m ) f(m) f(m),其中 m m m定义在任意一个集合 S ⊂ { 0 , 1 } l \mathcal S \subset \{0, 1\}^l S⊂{0,1}l中,并且 f ( m ) f(m) f(m)输出 的值是0-1比特。也即,攻击者利用密文 c c c算对函数 f ( m ) f(m) f(m)的概率应该和攻击者什么都不知道没有太多的差别。(否则就是泄露了信息)。
基于上述叙述,我们给出语义安全性的定义:
定义. 一个加密方案 ( E n c , D e c ) (Enc, Dec) (Enc,Dec)在窃听攻击下是语义安全的,如果对于任意的PPT算法 A \mathcal A A,都有一个PPT算法 A ′ \mathcal A' A′,使得下列东西是小量:
∣ P [ A ( 1 n , E n c k ( m ) , h ( m ) ) = f ( m ) ] − P [ A ′ ( 1 n , ∣ m ∣ , h ( m ) ) = f ( m ) ] ∣ |P[\mathcal A(1^n, Enc_k(m), h(m))=f(m)] - P[\mathcal A'(1^n, |m|, h(m))=f(m)]| ∣P[A(1n,Enck(m),h(m))=f(m)]−P[A′(1n,∣m∣,h(m))=f(m)]∣
其中 h ( m ) h(m) h(m)是攻击者已经掌握的外部消息。在语义安全性中,攻击者用算法 A \mathcal A A在给定 c = E n c k ( m ) c=Enc_k(m) c=Enck(m)、 h ( m ) h(m) h(m)的情况下计算 m m m的函数 f ( m ) f(m) f(m),它的效果应该和攻击者用任意一个算法 A ′ \mathcal A' A′在给定 h ( m ) h(m) h(m)和 ∣ m ∣ |m| ∣m∣的情况下计算 f ( m ) f(m) f(m)差不多。
定理. 计算不可区分性和语义安全性等价。
伪随机性和流密码
伪随机数生成器 G G G是一个高效的(多项式时间)、确定性的算法,可以将一个短的、采样自均匀分布的比特串(种子, seed)转化成一个长的、看起来采样自均匀分布的比特串。
研究伪随机数的意义在于从统计意义上模拟随机性。为了判断出各种伪随机数究竟不随机在哪儿,可以构造出各种各样的统计量。
一个问题在于,如何判断伪随机数的随机性?类似于计算安全性,我们可以想出来一个类似于计算随机性的东西:一个好的伪随机数生成器需要骗过所有(可以高效地计算)的统计量。
于是,我们给出正式定义:
定义. l l l是一个多项式, G G G是一个确定性的多项式时间算法,使得对于任意的 n n n(安全参数,在这里是种子的长度)和任意的输入 s ∈ { 0 , 1 } n s \in \{0, 1\}^n s∈{0,1}n(这是随机种子), G ( s ) G(s) G(s)是长度为 l ( n ) l(n) l(n)的串。我们说 G G G是伪随机数生成器,如果:
- 对于任意的 n n n,有 l ( n ) > n l(n) > n l(n)>n
- 对于任意的概率多项式时间算法
D
D
D,存在一个小量
ϵ
(
n
)
\epsilon(n)
ϵ(n)使得
∣ P [ D ( G ( s ) ) = 1 ] − P [ D ( r ) = 1 ] ∣ ≤ ϵ ( n ) |P[D(G(s))=1] - P[D(r) = 1]| \leq \epsilon(n) ∣P[D(G(s))=1]−P[D(r)=1]∣≤ϵ(n)
其中,我们称 l l l是伪随机数生成器的扩张因子。我们认为 D D D是随机性判别器, D ( ⋅ ) = 1 D(·)=1 D(⋅)=1表明,它认为输入的东西是随机的,反之它认为输入的东西不是随机的。 s ∈ { 0 , 1 } n s \in \{0, 1\}^n s∈{0,1}n, r ∈ { 0 , 1 } l ( n ) r\in \{0, 1\}^{l(n)} r∈{0,1}l(n)均采样自均匀分布。
实际上,伪随机数生成的东西显然不是均匀的。比如设我们有 n n n比特的种子, l ( n ) = 2 n l(n) = 2n l(n)=2n。确定性映射 G G G最多将 2 n 2^n 2n个种子映射到像空间( 2 n 2^n 2n个值),而 { 0 , 1 } 2 n \{0, 1\}^{2n} {0,1}2n空间中还有 2 2 n − 2 n 2^{2n}-2^n 22n−2n个值没有映射到。
另一个问题是,伪随机数生成器是不是真的存在?实际上我们不知道怎么无条件地证明伪随机数的存在,但是我们有很站得住脚的原因可以相信它存在。首先,如果假设单向函数(单向函数 f f f具有性质:给定 x x x计算 f ( x ) f(x) f(x)是容易的,但是给定 f ( x ) f(x) f(x)计算原像是难的。典型的例子是哈希函数)是存在的,我们就可以基于单向函数构造伪随机数生成器。单向函数存在这一假设是很弱的假设。另外,已经有很多的伪随机数生成器(比如流密码),而且目前还没找到高效的 D D D。
流密码
流密码和伪随机数生成器有一点不同:它可以生成任意多的“随机”比特。
我们定义流密码为两个函数: ( I n i t , G e t B i t s ) (Init, GetBits) (Init,GetBits):
- Init入参包括:种子 s s s和(可选的)初始化向量 I V IV IV。输出一个初始状态 x 0 x_0 x0
- GetBits的入参包括:状态 x k x_k xk,输出一个比特 y k y_k yk然后更新状态为 x k + 1 x_{k+1} xk+1
于是,如果我们让流密码在初始化后运行 l l l次 G e t B i t s GetBits GetBits,就可以得到一个可能的“伪随机数生成器”,记为 G l G_l Gl。
粗略地说,上面的流密码是安全的,如果它不需要 I V IV IV,并且对于任意的多项式 l ( n ) l(n) l(n),其中 l ( n ) > n l(n) > n l(n)>n, G l G_l Gl都是扩张因子为 l l l的伪随机数生成器。




![[C++] 类与对象(中)完整讲述运算符重载示例 -- 日期类(Date) -- const成员](https://img-blog.csdnimg.cn/img_convert/d0bcbdf40c5df492dcddcb68255c5870.png)