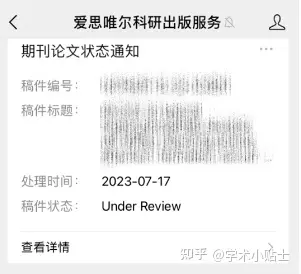
Alice 和 Bob 用几堆石子在做游戏。一共有偶数堆石子,排成一行;每堆都有 正 整数颗石子,数目为 piles[i] 。
游戏以谁手中的石子最多来决出胜负。石子的 总数 是 奇数 ,所以没有平局。
Alice 和 Bob 轮流进行,Alice 先开始 。 每回合,玩家从行的 开始 或 结束 处取走整堆石头。
这种情况一直持续到没有更多的石子堆为止,此时手中 石子最多 的玩家 获胜 。假设 Alice 和 Bob 都发挥出最佳水平,当 Alice 赢得比赛时返回 true ,当 Bob 赢得比赛时返回 false 。
示例 1:
输入:piles = [5,3,4,5]
输出:true
解释: Alice 先开始,只能拿前 5 颗或后 5 颗石子 。 假设他取了前 5
颗,这一行就变成了 [3,4,5] 。 如果 Bob 拿走前 3 颗,那么剩下的是 [4,5],Alice 拿走后 5 颗赢得 10 分。
如果 Bob 拿走后 5 颗,那么剩下的是 [3,4],Alice 拿走后 4 颗赢得 9 分。 这表明,取前 5 颗石子对 Alice
来说是一个胜利的举动,所以返回 true 。
示例 2:
输入:piles = [3,7,2,3] 输出:true
提示:
2 <= piles.length <= 500
piles.length 是 偶数
1 <= piles[i] <= 500
sum(piles[i]) 是 奇数
解题思路:
dfs + 备忘录,思路和预测赢家一样
预测赢家
代码:
import java.util.*;
class Solution {
int INF = Integer.MAX_VALUE;
public boolean stoneGame(int[] piles) {
int len = piles.length;
int memo[][] = new int[len][len];
for(int i = 0; i < len; i ++) Arrays.fill(memo[i], INF);
return dfs(0, len - 1, piles, memo) > 0;
}
public int dfs(int i, int j, int piles[], int memo[][]) {
if(i > j) return 0;
if(memo[i][j] != INF) return memo[i][j];
int chooseFirst = piles[i] - dfs(i + 1, j, piles, memo);
int chooseLast = piles[j] - dfs(i, j - 1, piles, memo);
memo[i][j] = Math.max(chooseFirst, chooseLast);
return memo[i][j];
}
}

数学

代码:
class Solution {
public boolean stoneGame(int[] piles) {
return true;
}
}



![[C++] 类与对象(中)完整讲述运算符重载示例 -- 日期类(Date) -- const成员](https://img-blog.csdnimg.cn/img_convert/d0bcbdf40c5df492dcddcb68255c5870.png)