Diffusion Model

【碎碎念】感觉Diffusion Model里面的数学公式太多了QwQ，所以自己稍微梳理一下。
我自己是听B站的课程：李宏毅课程听懂的，感觉讲得很清楚

概念模型

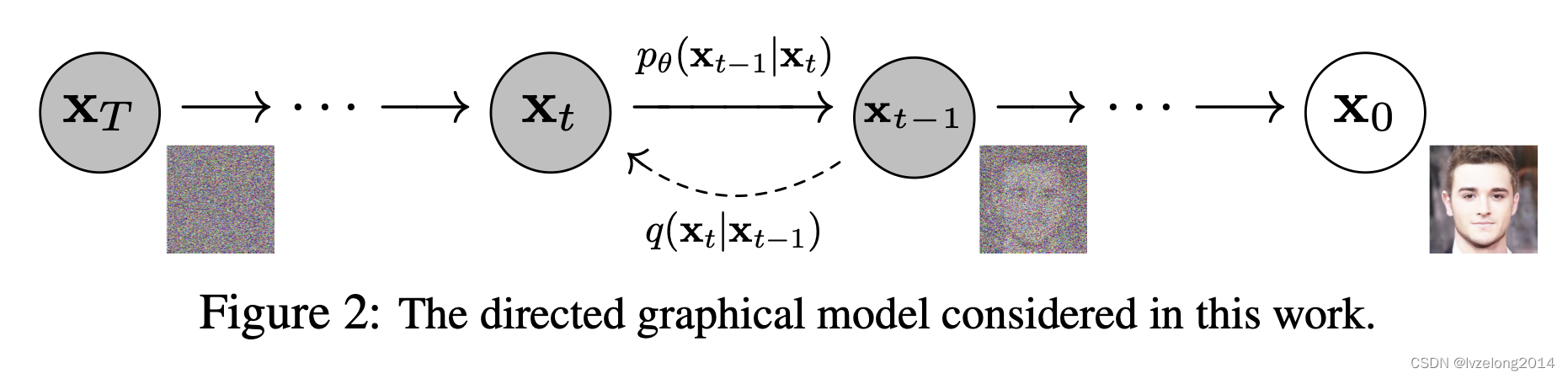
Diffusion Model的基本思想就是：

• 把一张图片通过$T$step 添加高斯噪声，最后会形成一个高斯分布，$\mathcal{N}(0,\mathbf{I})$
• 把添加噪声的每步图片$x_0\cdots x_T$看成随机过程，则形成一个马尔可夫链，每一步是已知的$q(x_t|x_{t-1})$
• 设置一个Network，网络中的参数$\theta$作为先验，如果能预测出逆过程$p_{\theta }(x_{t-1}|x_t)$，就可以从噪声图片生成图片

算法流程

主算法流程如上图，解释以下大致思路：
训练部分：

• Sample一张图片${\mathbf{x}}_0$
• 选择一个步骤$t$
• 优化目标：Denoise网络，给定$t$和$t$步的噪图，能够预测$t-1$步到$t$步添加的噪声长什么样子

推理部分：

• Sample一张噪图
• 从$T$步开始一步一步通过Denoise推理出真实图片

实际上上述只是一个非常粗略的解释，要真正理解这个算法，还有如下几个问题要解决：

1. 如何生成$t$步的噪图
2. 形式化Denoise的优化目标

生成t步的噪图

每一步逐渐混入方差为${\beta }_i$的高斯噪声，得到下面的式子
$$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$$
用重参数化的写法是：
$$\begin{gathered} {\mathbf{x}}_{\mathbf{t}}=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+{\sqrt{\beta }}_t{ϵ}_t \\ {ϵ}_t\sim \mathcal{N}(0,\mathbf{I}) \end{gathered}$$

进一步推到

$$\begin{gathered} {\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}{ϵ}_t \\ =\sqrt{1-{\beta }_t}(\sqrt{1-{\beta }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{{\beta }_{t-1}}{ϵ}_{t-1})+\sqrt{{\beta }_t}{ϵ}_t \\ =\sqrt{(1-{\beta }_t)(1-{\beta }_{t-1})}{\mathbf{x}}_{t-2}+\sqrt{1-(1-{\beta }_t)(1-{\beta }_{t-1})}ϵ \\ =\cdots \\ =\sqrt{{\alpha }_t}{\mathbf{x}}_0+\sqrt{1-{\alpha }_t}ϵ, \\ {\alpha }_t=\prod _{i=1}^{t}1-{\beta }_t \end{gathered}$$

这是根据高斯的可加性原理推导得出的结论。也就是，不需要一步步加，可以一次性推导到位。

优化目标

假设整体的$T$步网络生成的概率分布是$p_{\theta }$，那么其实优化的目标可以是：
$$\underset{\theta }{\max }{\mathbb{E}}_{x_0\sim p_{data}(x_0)}[log{p}_{\theta }({\mathbf{x}}_0)]$$

这个优化目标可以解释为Sample所有数据集的图片，这些图片被$p_{\theta }$ 生成的概率乘积最大（取了个log）

接下来其实利用了一个著名的VLB（变分下界）的定理，这个定理再VAE中使用过，具体的证明可以看视频，这里直接出结论：
$$\log p_{\theta }({\mathbf{x}}_0)\ge {\mathbb{E}}_{{\mathbf{x}}_1\cdots {\mathbf{x}}_T\sim q({\mathbf{x}}_1\cdots {\mathbf{x}}_T|{\mathbf{x}}_0)}[\log \frac{p_{\theta }({\mathbf{x}}_0\cdots {\mathbf{x}}_T)}{q({\mathbf{x}}_1\cdots {\mathbf{x}}_T|{\mathbf{x}}_0)}]$$

原论文经过了一番精彩的数学推导（注意，这段推导是取符号转化成最小化的Loss，所以符号要反着看）：


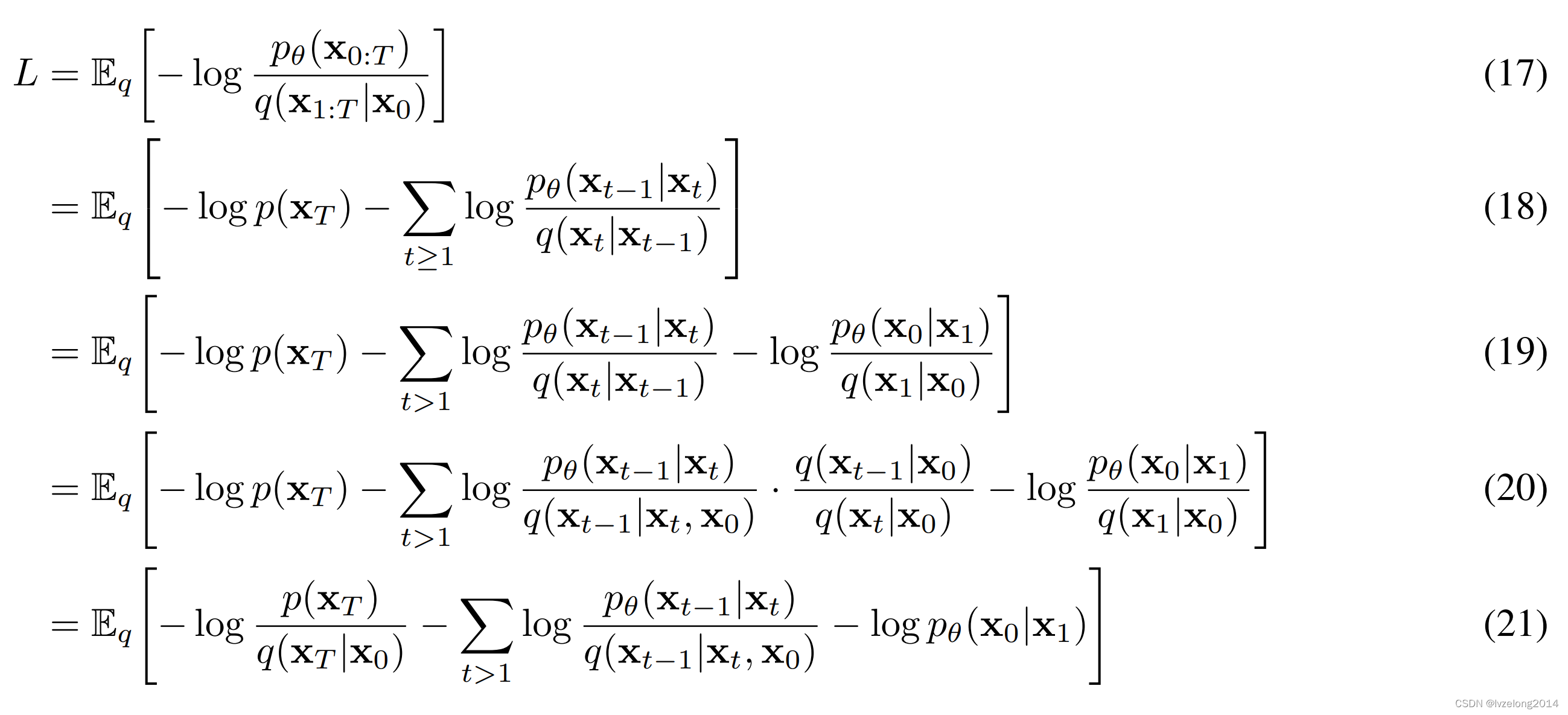
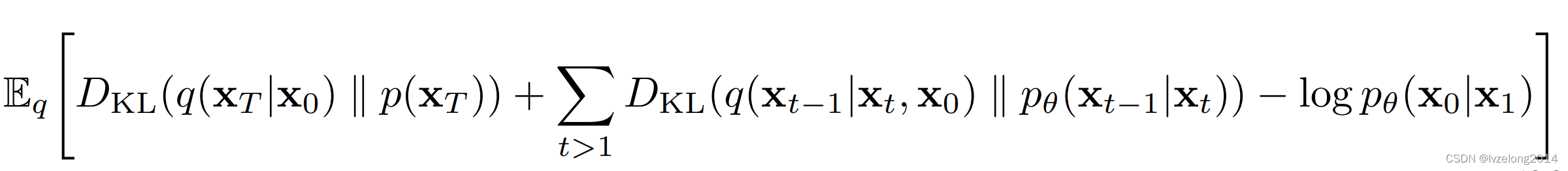
关于这段推导变换的精妙之处，先占个坑，暂时没想出来~
注意到$p({\mathbf{x}}_T)$就是变换到最后的噪声图，而$q({\mathbf{x}}_T|{\mathbf{x}}_0)$是一个固定的过程，这两者都和网络没关系，所以可以直接在优化项中舍去。

$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)$的推导

$$q(x_{t-1}|x_t,x_0)=\frac{q(x_{t-1},x_t,x_0)}{q(x_t,x_0)}=\frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)q(x_0)}{q(x_t|x_0)q(x_0)}=\frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)}{q(x_t|x_0)}$$
发现等式后面每项都是已知的，然后开始经过一番魔幻推导

结果就是还是一个高斯分布
梳理一下思路：我们现在有两个高斯分布$q(x_{t-1}|x_t,x_0)$，$p_{\theta }(x_{t-1}|x_t)$，后者就是我们的降噪网络，我们的目标是让我们的降噪网络和$q(x_{t-1}|x_t,x_0)$的分布尽量接近。
再进一步思考，实际上$q(x_{t-1}|x_t,x_0)$的意思就是给定初始图片，$t\to t-1$这个逆过程的分布
而我们的网络是要生成一个降噪网络，这个优化目标告诉我们，需要在没有初始图片的情况下去拟合这个$t\to t-1$
非常的合理，只不过使用了严谨的数学公式去推导了这个过程罢了。
关于最后一项，说是和VAE类似的处理方法，先占个坑，不解释

优化过程

• $q(x_{t-1}|x_t,x_0)$是一个高斯分布，那我们让$p_{\theta }(x_{t-1}|x_t)$也是高斯分布就行了。
• $q(x_{t-1}|x_t,x_0)$的方差是确定的，那我们让$p_{\theta }(x_{t-1}|x_t)$的方差和它一样就行了
• 所以最后我们需要最小化的，就是两者的平均值。

继续化简

我们让两者形式一致，最后我们需要predict只剩下最后一小项

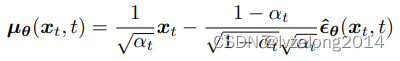
这就是Alog1，2的来源
这篇文章到这里就暂告一段落了，参考文献：
https://arxiv.org/pdf/2208.11970.pdf