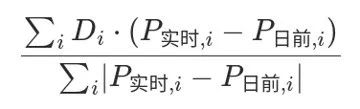第一章 回溯法
1.1 马拦过河卒
| 源程序名 knight.???(pas, c, cpp) 可执行文件名 knight.exe 输入文件名 knight.in 输出文件名 knight.out |
【问题描述】
棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上C点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,A点(0, 0)、B点(n, m)(n, m为不超过15的整数),同样马的位置坐标是需要给出的。现在要求你计算出卒从A点能够到达B点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
【输入】
一行四个数据,分别表示B点坐标和马的坐标。
【输出】
一个数据,表示所有的路径条数。
【样例】
knight.in knight.out
6 6 3 3 6
【算法分析】
从起点开始往下走(只有两个方向可以走),如果某个方向可以走再继续下一步,直到终点,此时计数。最后输出所有的路径数。这种方法可以找出所有可能走法,如果要输出这些走法的话这种方法最合适了,但是本题只要求输出总的路径的条数,当棋盘比较大时,本程序执行会超时,此时最好能找出相应的递推公式更合适,详见后面的递推章节。
1.2 出栈序列统计
| 源程序名 stack1.???(pas, c, cpp) 可执行文件名 stack1.exe 输入文件名 stack1.in 输出文件名 stack1.out |
【问题描述】
栈是常用的一种数据结构,有n令元素在栈顶端一侧等待进栈,栈顶端另一侧是出栈序列。你已经知道栈的操作有两·种:push和pop,前者是将一个元素进栈,后者是将栈顶元素弹出。现在要使用这两种操作,由一个操作序列可以得到一系列的输出序列。请你编程求出对于给定的n,计算并输出由操作数序列1,2,…,n,经过一系列操作可能得到的输出序列总数。
【输入】
一个整数n(1<=n<=15)
【输出】
一个整数,即可能输出序列的总数目。
【样例】
stack1.in stack1.out
3 5
【算法分析】
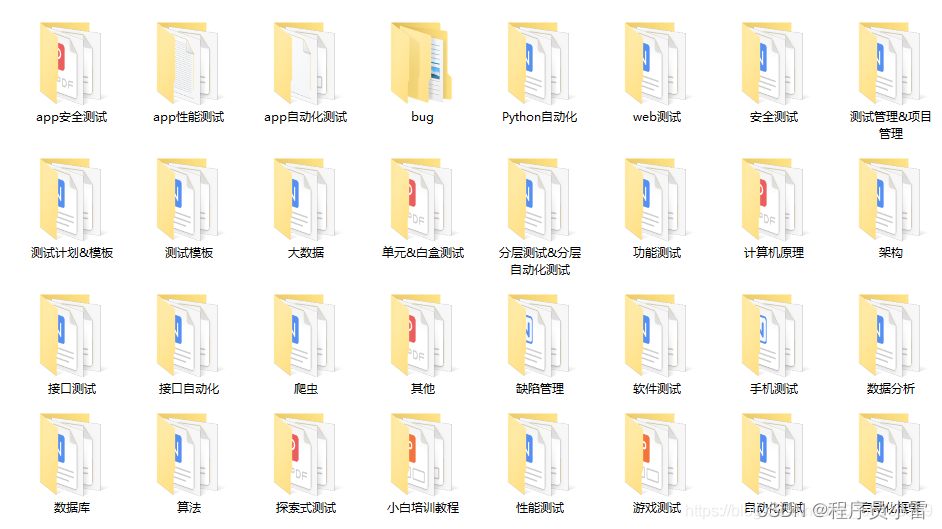
先了解栈的两种基本操作,进栈push就是将元素放入栈顶,栈顶指针上移一位,等待进栈队列也上移一位,出栈pop是将栈顶元素弹出,同时栈顶指针下移一位。
用一个过程采模拟进出栈的过程,可以通过循环加递归来实现回溯:重复这样的过程,如果可以进栈则进一个元素,如果可以出栈则出一个元素。就这样一个一个地试探下去,当出栈元素个数达到n时就计数一次(这也是递归调用结束的条件)。
1.3 算24点
| 源程序名 point24.???(pas, c, cpp) 可执行文件名 point24.exe 输入文件名 point24.in 输出文件名 point24.out |
【问题描述】
几十年前全世界就流行一种数字游戏,至今仍有人乐此不疲.在中国我们把这种游戏称为“算24点”。您作为游戏者将得到4个1~9之间的自然数作为操作数,而您的任务是对这4个操作数进行适当的算术运算,要求运算结果等于24。
您可以使用的运算只有:+,-,*,/,您还可以使用()来改变运算顺序。注意:所有的中间结果须是整数,所以一些除法运算是不允许的(例如,(2*2)/4是合法的,2*(2/4)是不合法的)。下面我们给出一个游戏的具体例子:
若给出的4个操作数是:1、2、3、7,则一种可能的解答是1+2+3*7=24。
【输入】
只有一行,四个1到9之间的自然数。
【输出】
如果有解的话,只要输出一个解,输出的是三行数据,分别表示运算的步骤。其中第一行是输入的两个数和一个运算符和运算后的结果,第二行是第一行的结果和一个输入的数据、运算符、运算后的结果;第三行是第二行的结果和输入的一个数、运算符和“=24”。如果两个操作数有大小的话则先输出大的。
如果没有解则输出“No answer!”
【样例】
point24.in point24.out
1 2 3 7 2+1=3
7*3=21
21+3=24
【算法分析】
计算24点主要应用四种运算.开始状态有四个操作数,一个运算符对应两个操作数,所以一开始选择两个操作数分别对四个操作符进行循环检测,每一次运算后产生了新的数,两个数运算变成一个数,整体是少了一个操作数,所以四个数最终是三次运算。由于操作的层数比较少(只有三层),所以可以用回溯的算法来进行检测,当找到一个解时便结束查找。如果所有的情况都找过后仍然没有,则输出无解的信息。
1.4 冗余依赖
| 源程序名 redund.???(pas, c, cpp) 可执行文件名 redund.exe 输入文件名 redund.in 输出文件名 redund.out |
【问题描述】
在设计关系数据库的表格时,术语“函数依赖”(FD)被用来表示不同域之间的关系。函数依赖是描述一个集合中的域的值与另一个集合中的域的值之间的关系。记号X->Y被用来表示当集合X中的域被赋值后,集合Y的域就可以确定相应的值。例如,一个数据表格包含“社会治安编号”(S)、“姓名”(N)、“地址”(A)、“电话”(P)的域,并且每个人都与某个特定的互不相同的S值相对应,根据域S就可以确定域N、A、P的值。这就记作S->NAP。
写一个程序以找出一组依赖中所有的冗余依赖。一个依赖是冗余的是指它可以通过组里的其他依赖得到。例如,如果组里包括依赖A->B、B->C和A->C,那么第三个依赖是冗余的,因为域C可以用前两个依赖得到(域A确定了域B的值,同样域B确定了域C的值)。在A->B、B->C、C->A、A->C、C->B和B->A中,所有的依赖都是冗余的。
现在要求你编写一个程序,从给定的依赖关系中找出冗余的。
【输入】
输A的文件第一行是一个不超过100的整数n,它表示文件中函数依赖的个数。从第二行起每一行是一个函数依赖且互不重复,每行包含用字符“-”和“>”隔开的非空域列表。列表月包含大写的字母,函数依赖的数据行中不包括空格和制表符,不会出现“平凡”冗余依赖(如A->A)。虽然文件中没有对函数依赖编号,但其顺序就是编号1到n。
【输出】
每一个冗余依赖,以及其他依赖的一个序列以说明该依赖是冗余的,先是一个FD,然后是依赖函数号,接着是"is redundant using FDs:”最后是说明的序列号。
如果许多函数依赖的序列都能被用来说明一个依赖是冗余的,则输出其中最短的证明序列。如果这些函数依赖中不包含冗余依赖,则输出“No redundant FDs”信息。
【样例1】 【样例2】
redund.in redund.out redund.in redund.out
3 FD 3 is redundant using FDs: 1 2 6 FD 3 is redundant using FDs: 1
A->BD {即C可以通过1、2得到} P->RST FD 5 is redundant using FDs: 4 6 2
BD->C VRT->SQP
A->C PS->T
Q->TR
QS->P
SR->V
【算法分析】
一个依赖冗余,就是说它可以由其他依赖推导出来。如何判断一个依赖能否被其他依赖推导出来呢?假设判断的依赖为“a->b”,先找出所有形式为“a->*”的依赖,再由*开始找相关依赖,直到出现“#->b”为止(这里a、b、*、#都表示任意一个域名)。
如何实现这种查找呢?可以通过筒单的回溯来完成。只是找出冗余(如果有的话)还不说明工作就已结束,要到找出所有的能够推导出b的依赖序列,选出其中长度最短的(最短的也可能并不惟一,因此本题答案有可能并不惟一),最短的证明序列中一定不存在多余的依赖,如果不是最短的证明序列,那么该证明序列中就有可能还有冗余依赖。
1.5 走迷宫
| 源程序名 maze.???(pas, c, cpp) 可执行文件名 maze.exe 输入文件名 maze.in 输出文件名 maze.out |
【问题描述】
有一个m*n格的迷宫(表示有m行、n列),其中有可走的也有不可走的,如果用1表示可以走,0表示不可以走,文件读入这m*n个数据和起始点、结束点(起始点和结束点都是用两个数据来描述的,分别表示这个点的行号和列号)。现在要你编程找出所有可行的道路,要求所走的路中没有重复的点,走时只能是上下左右四个方向。如果一条路都不可行,则输出相应信息(用-l表示无路)。
【输入】
第一行是两个数m,n(1<m,n<15),接下来是m行n列由1和0组成的数据,最后两行是起始点和结束点。
【输出】
所有可行的路径,描述一个点时用(x,y)的形式,除开始点外,其他的都要用“一>”表示方向。
如果没有一条可行的路则输出-1。
【样例】
maze.in
5 6
1 0 0 1 0 1
1 1 1 1 1 1
0 0 1 1 1 0
1 1 1 1 1 0
1 1 1 0 1 1
1 1
5 6
maze.out
(1,2)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
【算法分析】
用一个a数组来存放迷宫可走的情况,另外用一个数组b来存放哪些点走过了。每个点用两个数字来描述,一个表示行号,另一个表示列号。对于某一个点(x,y),四个可能走的方向的点描述如下表:
| 1 | ||
| 4 | x,y | 2 |
| 3 |
对应的位置为:(x-1, y),(x, y+1),(x+1, y),(x, y-1)。所以每个点都要试探四个方向,如果没有走过(数组b相应的点的值为0)且可以走(数组a相应点的值为1)同时不越界,就走过去,再看有没有到达终点,到了终点则输出所走的路,否则继续走下去。
这个查找过程用search来描述如下:
procedure search(x, y, b, p);{x,y表示某一个点,b是已经过的点的情况,p是已走过的路}
begin
for i:=1 to 4 do{分别对4个点进行试探}
begin
先记住当前点的位置,已走过的情况和走过的路;
如果第i个点(xl,y1)可以走,则走过去;
如果已达终点,则输出所走的路径并置有路可走的信息,
否则继续从新的点往下查找search(xl,y1,b1,p1);
end;
end;
【思考与提高】
该程序通过引进新的变量和数组来继续新的查找,如果不引进新的变量和数组,那么每一次返回时要将原来的值还原才行,如果那样,程序应如何修改?其实那样更加符合回溯的思想——换条路再试。这类问题也可以归为搜索的问题,如果m和n的值相对比较大,则解可能很多,若题目只要找到一条路就结束程序时,在程序的输出部分后面加上一个halt就行了。
有些情况很明显是无解的,如从起点到终点的矩形中有一行或一列都是为0的,明显道路不通,对于这种情况要很快地“剪掉”多余分枝得出结论,这就是搜索里所说的“剪枝”。从起点开始往下的一层层的结点,看起来如同树枝一样,对于其中的“枯枝”——明显无用的节点可以先行“剪掉”,从而提高搜索速度。
1.6 单向双轨道
| 源程序名 track.???(pas, c, cpp) 可执行文件名 track.exe 输入文件名 track.in 输出文件名 track.out |
【问题描述】
![]()
正在上传…重新上传取消 如图所示l,某火车站有B,C两个调度站,左边入口A处有n辆火车等待进站(从左到右以a、b、c、d编号),右边是出口D,规定在这一段,火车从A进入经过B、C只能从左向右单向开,并且B、C调度站不限定所能停放的车辆数。
从文件输入n及n个小写字母的一个排列,该排列表示火车在出口D处形成的从左到右的火车编号序列。输出为一系列操作过程,每一行形如“h L R”的字母序列,其中h为火车编号,L为h车原先所在位置(位置都以A、B、C、D表示),R为新位置。或者输出‘NO’表示不能完成这样的调度。
【输入】
一个数n(1<n<27)及由n个小写字母组成的字符串。
【输出】
可以调度则输出最短的调度序列,不可以调度时则输出‘NO’。
【样例】
track.in track.out
3 c A B
cba b A C
a A D
b C D
c B D
【算法分析】
这是一道类似于栈的操作题目,只不过是有两个栈B和C可以操作,而对于A序列里的元素,既可以进入B,也可以进入C,或直接到D。解决问题可以从D序列出发反过来看,当前要到D的字符在哪里,如果在A,再看它前面有没有字符,如果有,先让它们进栈(B或C),否则直接到D;如果在B,看是否是栈顶元素,如果是,直接到D,否则将上面的字符进C;如果在C,看是否是栈顶元素,如果是,直接到D,否则无法进行操作,因为只能向右不能向左,这时要回溯。如果所有的情况都检测过,某个字符不能进行到D的操作,则输出无解信息。
由于A里的非直接进入D的字符可以进入B或C,可以跟二进制建立起对应关系,将所有情况列举一遍,再找出其中步骤最少的输出。
1.7 组合的输出
| 源程序名 track.???(pas, c, cpp) 可执行文件名 track.exe 输入文件名 track.in 输出文件名 track.out |
【问题描述】
排列与组合是常用的数学方法,其中组合就是从n个元素中抽出r个元素(不分顺序且r<=n),我们可以简单地将n个元素理解为自然数1,2,…,n,从中任取r个数。
现要求你不用递归的方法输出所有组合。
例如n=5,r=3,所有组合为:
l 2 3 l 2 4 1 2 5 l 3 4 l 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
【输入】
一行两个自然数n、r(1<n<21,1<=r<=n)。
【输出】
所有的组合,每一个组合占一行且其中的元素按由小到大的顺序排列,每个元素占三个字符的位置,所有的组合也按字典顺序。
【样例】
compages.in compages.out
5 3 1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
【算法分析】
如果通过循环加递归来实现回溯比较简单,相应程序为:
| const max=20; var a:array[0..max]of integer; n,r:1..max; procedure compages(k:integer);{选取第k个元素} var i,j:integer; begin {当前所选元素最小为前一个元素加1,最大为n-(r-k),因为后面还有(r-k)个元素要选取,至少为每次选取留一个} for i:=a[k-1]+1 to n-(r-k) do begin a[k]:=i; {选取一个元素} if k=r then begin for j:=1 to r do write(a[j]:3); writeln; end else compages(k+1); end; end; begin {main} readln(n,r); compages(1); {从第一个元素开始选取给合数} end. |
本题要求不用递归来实现回溯,关键要定好回溯的条件。如果选取第i个元素时选择了a[i],根据输出条件应有a[i]-i<=n-r,如果不满足这个条件说明当前第i个元素已再无数可取,要进行回溯,将其值减1,退到上一步将上一步原来的值再增加1,重复上述过程。当全部选取完时,i回到了0,a[0]的值增加1后变为1,这是整个选取过程结束的条件。
1.8 售货员的难题
| 源程序名 salesman.???(pas, c, cpp) 可执行文件名 salesman.exe 输入文件名 salesman.in 输出文件名 salesman.out |
【问题描述】
某乡有n个村庄(1<n<40),有一个售货员,他要到各个村庄去售货,各村庄之间的路程s(0<s<1000)是已知的,且A村到B村与B村到A村的路大多不同。为了提高效率,他从商店出发到每个村庄一次,然后返回商店所在的村,假设商店所在的村庄为1,他不知道选择什么样的路线才能使所走的路程最短。请你帮他选择一条最短的路。
【输入】
村庄数n和各村之间的路程(均是整数)。
【输出】
最短的路程。
【样例】
salesman.in salesman.out
3 {村庄数} 3
0 2 l {村庄1到各村的路程}
1 0 2 {村庄2到各村的路程}
2 1 0 {村庄3到各村的路程}
【算法分析】
题目给定的村庄数不多(≤40),所以可以用回溯的方法,从起点(第一个村庄)出发找出所有经过其他所有村庄的回路,计算其中的最短路程。当村庄数n比较大时这种方法就不太适用了。
用一个过程road(step,line:byte)来描述走的状况,其中step是当前已到村庄数、line是当前所在的村庄。如果step=n,下面只能回起点了,直接看第line个村庄到第一个村庄的路程加上已走的总路程,如果比最小值还小则替换最小值(要保存路径的话也可保存,这是回溯算法的优点,考虑到达最小值的路径可能不止一条,不便于测试,题目没要求输出路径)。如果step还小于n,那么将还没有到过的村庄一个一个地试过去,再调用下一步road(step+1,新到的村庄号)。
1.9 驾车旅游
| 源程序名 tour.???(pas, c, cpp) 可执行文件名 tour.exe 输入文件名 tour.in 输出文件名 tour.out |
【问题描述】
如今许多普通百姓家有了私家车,一些人喜爱自己驾车从一个城市到另一个城市旅游。自己驾车旅游时总会碰到加油和吃饭的问题,在出发之前,驾车人总要想方设法得到从一个城市到另一个城市路线上的加油站的列表,列表中包括了所有加油站的位置及其每升的油价(如3.25元/L)。驾车者一般都有以下的习惯:
(1)除非汽车无法用油箱里的汽油达到下一个加油站或目的地,在油箱里还有不少于最大容量一半的汽油时,驾驶员从不在加油站停下来;
(2)在第一个停下的加油站总是将油箱加满;
(3)在加油站加油的同时,买快餐等吃的东西花去20元。
(4)从起始城市出发时油箱总是满的。
(5)加油站付钱总是精确到0.1元(四舍五入)。
(6)驾车者都知道自己的汽车每升汽油能够行驶的里程数。
现在要你帮忙做的就是编写一个程序,计算出驾车从一个城市到另一个城市的旅游在加油和吃饭方面最少的费用。
【输入】
第一行是一个实数,是从出发地到目的地的距离(单位:km)。
第二行是三个实数和一个整数,其中第一个实数是汽车油箱的最大容量(单位:I。);第二个实数是汽车每升油能行驶的公里数;第三个实数是汽车在出发地加满油箱时的费用(单位元);一个整数是1到50间的数,表示从出发地到目的地线路上加油站的数目。
接下来n行都是两个实数,第一个数表示从出发地到某一个加油站的距离(单位:km);第二个实数表示该加油站汽油的价格(单位:元)。
数据项中的每个数据都是正确的,不需判错。一条线路上的加油站根据其到出发地的距离递增排列并且都不会大于从出发地到目的地的距离。
【输出】
就一个数据,是精确到0.1元的最小的加油和吃饭费用
【样例】
tour.in tour.out
600 379.6
40 8.5 128 3
200 3.52
350 3.45
500 365
【算法分析】
驾车者从出发地出发后对于每个加油站都可能有两种操作,一是进去加油买食品,二是不进去继续前行(如果当前汽车的余油可以的话),这样有n个加油站最多可能有2n种选择。由于加油站数目不太多,可以采用回溯的算法来解决问题。从第一个加油站开始,依次选择所要停下的下一个加油站,从而找出总费用最少的方案,加油站数目最多为50,这样回溯不会进行得很深。在选择下一个要停下的加油站时比较麻烦,不能完全一个一个地试过去,这样时间太长。可以用这样的方法:先找出第一个要停下的加油站,判断其后面的加油站是否可以到达,如果不可到达就必须在这里停下来加油;否则就找出可以到达但如果只用一半汽油则无法到达的所有加油站,依次进行停靠。
1.10关路灯
| 源程序名 power.???(pas, c, cpp) 可执行文件名 power.exe 输入文件名 power.in 输出文件名 power.out |
【问题描述】
某一村庄在一条路线上安装了n盏路灯,每盏灯的功率有大有小(即同一段时间内消耗的电量有多有少)。老张就住在这条路中间某一路灯旁,他有一项工作就是每天早上天亮时一盏一盏地关掉这些路灯。
为了给村里节省电费,老张记录下了每盏路灯的位置和功率,他每次关灯时也都是尽快地去关,但是老张不知道怎样去关灯才能够最节省电。他每天都是在天亮时首先关掉自己所处位置的路灯,然后可以向左也可以向右去关灯。开始他以为先算一下左边路灯的总功率再算一下右边路灯的总功率,然后选择先关掉功率大的一边,再回过头来关掉另一边的路灯,而事实并非如此,因为在关的过程中适当地调头有可能会更省一些。
现在已知老张走的速度为1m/s,每个路灯的位置(是一个整数,即距路线起点的距离,单位:m)、功率(W),老张关灯所用的时间很短而可以忽略不计。
请你为老张编一程序来安排关灯的顺序,使从老张开始关灯时刻算起所有灯消耗电最少(灯关掉后便不再消耗电了)。
【输入】
文件第一行是两个数字n(0<n<50,表示路灯的总数)和c(1<=c<=n老张所处位置的路灯号);
接下来n行,每行两个数据,表示第1盏到第n盏路灯的位置和功率。
【输出】
一个数据,即最少的功耗(单位:J,1J=1W·s)。
【样例】
power.in power.out
5 3 270 {此时关灯顺序为3 4 2 1 5,不必输出这个关灯顺序}
2 10
3 20
5 20
6 30
8 10
【算法分析】
设老张开始所在位置为c,以起始点c为分界点,算出左右两部分总的功率p_left和p_right,再来分别看向左与向右的情况。
向左走时,相应地可以减小左边应费的功,而增加右边应费的功,如果到一个点(一盏路灯处)所要时间为t,减少的功为(p_left+w[i])*t,增加的功为p_right*2t。
向右走时,相应地可以减小右边应费的功,而增加左边应费的功,如果到一个点(一盏路灯处)所要时间为t,减少的功为(p_righ+w[i])*t,增加的功为p_left*2t。
比较向左与向右的情况,找出比较好的一种确定方法。大部分情况能够解出最小值,但不能求出所有情况下最佳的解。
对于每一个所处位置,都可以选择向左或向右,不管是向左还是向右,相应耗电的变化都跟上面所述一样。所以可以选择回溯的算法来实现有限的搜索,对每一个点试探向左与向右的情况,在所有可能的情况中找出最优解。
【思考与提高】
上面的程序运算的范围很有限,当n比较大时就会栈溢出,如n>30时速度就比较慢了。实际情况调头的次数并不会多的,到底在什么时候掉头根据情况而定。我们可以从最后一步来思考:
最后一次关的可能是第一个灯也可能是最后一个灯,哪种情况所费的功小就选哪种;
最后一次关的是第一个灯的话,说明最后的方向是从最后到最前(右边到左边),最后倒数第二次的方向为从左到右,起点可能是原始起点(此时是第一趟),也可能是原始起点左边的点(此时至少是第二趟),一个个地试过去,先设拐一次弯,有可能拐的点都试过去,再试有两次拐弯换方向的情况,当再多的拐弯超过已有的解时就不要再向下试了。采用这种回溯方法,效率更高。
如果n再大一些,如到300以上,上述方法也有它的局限性,此时最好从动态规划法或贪心法的角度去思考。
| 源程序名 maze.???(pas, c, cpp) 可执行文件名 maze.exe 输入文件名 maze.in 输出文件名 maze.out |
【问题描述】
有一个m*n格的迷宫(表示有m行、n列),其中有可走的也有不可走的,如果用1表示可以走,0表示不可以走,文件读入这m*n个数据和起始点、结束点(起始点和结束点都是用两个数据来描述的,分别表示这个点的行号和列号)。现在要你编程找出所有可行的道路,要求所走的路中没有重复的点,走时只能是上下左右四个方向。如果一条路都不可行,则输出相应信息(用-l表示无路)。
【输入】
第一行是两个数m,n(1<m,n<15),接下来是m行n列由1和0组成的数据,最后两行是起始点和结束点。
【输出】
所有可行的路径,描述一个点时用(x,y)的形式,除开始点外,其他的都要用“一>”表示方向。
如果没有一条可行的路则输出-1。
【样例】
maze.in
5 6
1 0 0 1 0 1
1 1 1 1 1 1
0 0 1 1 1 0
1 1 1 1 1 0
1 1 1 0 1 1
1 1
5 6
maze.out
(1,2)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(2,4)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(3,4)->(4,4)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(2,4)->(2,5)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(3,4)->(3,5)->(4,5)->(5,5)->(5,6)
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,4)->(4,5)->(5,5)->(5,6)
【算法分析】
用一个a数组来存放迷宫可走的情况,另外用一个数组b来存放哪些点走过了。每个点用两个数字来描述,一个表示行号,另一个表示列号。对于某一个点(x,y),四个可能走的方向的点描述如下表:
| 1 | ||
| 4 | x,y | 2 |
| 3 |
对应的位置为:(x-1, y),(x, y+1),(x+1, y),(x, y-1)。所以每个点都要试探四个方向,如果没有走过(数组b相应的点的值为0)且可以走(数组a相应点的值为1)同时不越界,就走过去,再看有没有到达终点,到了终点则输出所走的路,否则继续走下去。
这个查找过程用search来描述如下:
procedure search(x, y, b, p);{x,y表示某一个点,b是已经过的点的情况,p是已走过的路}
begin
for i:=1 to 4 do{分别对4个点进行试探}
begin
先记住当前点的位置,已走过的情况和走过的路;
如果第i个点(xl,y1)可以走,则走过去;
如果已达终点,则输出所走的路径并置有路可走的信息,
否则继续从新的点往下查找search(xl,y1,b1,p1);
end;
end;
【思考与提高】
该程序通过引进新的变量和数组来继续新的查找,如果不引进新的变量和数组,那么每一次返回时要将原来的值还原才行,如果那样,程序应如何修改?其实那样更加符合回溯的思想——换条路再试。这类问题也可以归为搜索的问题,如果m和n的值相对比较大,则解可能很多,若题目只要找到一条路就结束程序时,在程序的输出部分后面加上一个halt就行了。
有些情况很明显是无解的,如从起点到终点的矩形中有一行或一列都是为0的,明显道路不通,对于这种情况要很快地“剪掉”多余分枝得出结论,这就是搜索里所说的“剪枝”。从起点开始往下的一层层的结点,看起来如同树枝一样,对于其中的“枯枝”——明显无用的节点可以先行“剪掉”,从而提高搜索速度。
| 源程序名 track.???(pas, c, cpp) 可执行文件名 track.exe 输入文件名 track.in 输出文件名 track.out |
【问题描述】
![]()
正在上传…重新上传取消 如图所示l,某火车站有B,C两个调度站,左边入口A处有n辆火车等待进站(从左到右以a、b、c、d编号),右边是出口D,规定在这一段,火车从A进入经过B、C只能从左向右单向开,并且B、C调度站不限定所能停放的车辆数。
从文件输入n及n个小写字母的一个排列,该排列表示火车在出口D处形成的从左到右的火车编号序列。输出为一系列操作过程,每一行形如“h L R”的字母序列,其中h为火车编号,L为h车原先所在位置(位置都以A、B、C、D表示),R为新位置。或者输出‘NO’表示不能完成这样的调度。
【输入】
一个数n(1<n<27)及由n个小写字母组成的字符串。
【输出】
可以调度则输出最短的调度序列,不可以调度时则输出‘NO’。
【样例】
track.in track.out
3 c A B
cba b A C
a A D
b C D
c B D
【算法分析】
这是一道类似于栈的操作题目,只不过是有两个栈B和C可以操作,而对于A序列里的元素,既可以进入B,也可以进入C,或直接到D。解决问题可以从D序列出发反过来看,当前要到D的字符在哪里,如果在A,再看它前面有没有字符,如果有,先让它们进栈(B或C),否则直接到D;如果在B,看是否是栈顶元素,如果是,直接到D,否则将上面的字符进C;如果在C,看是否是栈顶元素,如果是,直接到D,否则无法进行操作,因为只能向右不能向左,这时要回溯。如果所有的情况都检测过,某个字符不能进行到D的操作,则输出无解信息。
由于A里的非直接进入D的字符可以进入B或C,可以跟二进制建立起对应关系,将所有情况列举一遍,再找出其中步骤最少的输出。
| 源程序名 track.???(pas, c, cpp) 可执行文件名 track.exe 输入文件名 track.in 输出文件名 track.out |
【问题描述】
排列与组合是常用的数学方法,其中组合就是从n个元素中抽出r个元素(不分顺序且r<=n),我们可以简单地将n个元素理解为自然数1,2,…,n,从中任取r个数。
现要求你不用递归的方法输出所有组合。
例如n=5,r=3,所有组合为:
l 2 3 l 2 4 1 2 5 l 3 4 l 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
【输入】
一行两个自然数n、r(1<n<21,1<=r<=n)。
【输出】
所有的组合,每一个组合占一行且其中的元素按由小到大的顺序排列,每个元素占三个字符的位置,所有的组合也按字典顺序。
【样例】
compages.in compages.out
5 3 1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
【算法分析】
如果通过循环加递归来实现回溯比较简单,相应程序为:
| const max=20; var a:array[0..max]of integer; n,r:1..max; procedure compages(k:integer);{选取第k个元素} var i,j:integer; begin {当前所选元素最小为前一个元素加1,最大为n-(r-k),因为后面还有(r-k)个元素要选取,至少为每次选取留一个} for i:=a[k-1]+1 to n-(r-k) do begin a[k]:=i; {选取一个元素} if k=r then begin for j:=1 to r do write(a[j]:3); writeln; end else compages(k+1); end; end; begin {main} readln(n,r); compages(1); {从第一个元素开始选取给合数} end. |
本题要求不用递归来实现回溯,关键要定好回溯的条件。如果选取第i个元素时选择了a[i],根据输出条件应有a[i]-i<=n-r,如果不满足这个条件说明当前第i个元素已再无数可取,要进行回溯,将其值减1,退到上一步将上一步原来的值再增加1,重复上述过程。当全部选取完时,i回到了0,a[0]的值增加1后变为1,这是整个选取过程结束的条件。
| 源程序名 salesman.???(pas, c, cpp) 可执行文件名 salesman.exe 输入文件名 salesman.in 输出文件名 salesman.out |
【问题描述】
某乡有n个村庄(1<n<40),有一个售货员,他要到各个村庄去售货,各村庄之间的路程s(0<s<1000)是已知的,且A村到B村与B村到A村的路大多不同。为了提高效率,他从商店出发到每个村庄一次,然后返回商店所在的村,假设商店所在的村庄为1,他不知道选择什么样的路线才能使所走的路程最短。请你帮他选择一条最短的路。
【输入】
村庄数n和各村之间的路程(均是整数)。
【输出】
最短的路程。
【样例】
salesman.in salesman.out
3 {村庄数} 3
0 2 l {村庄1到各村的路程}
1 0 2 {村庄2到各村的路程}
2 1 0 {村庄3到各村的路程}
【算法分析】
题目给定的村庄数不多(≤40),所以可以用回溯的方法,从起点(第一个村庄)出发找出所有经过其他所有村庄的回路,计算其中的最短路程。当村庄数n比较大时这种方法就不太适用了。
用一个过程road(step,line:byte)来描述走的状况,其中step是当前已到村庄数、line是当前所在的村庄。如果step=n,下面只能回起点了,直接看第line个村庄到第一个村庄的路程加上已走的总路程,如果比最小值还小则替换最小值(要保存路径的话也可保存,这是回溯算法的优点,考虑到达最小值的路径可能不止一条,不便于测试,题目没要求输出路径)。如果step还小于n,那么将还没有到过的村庄一个一个地试过去,再调用下一步road(step+1,新到的村庄号)。
| 源程序名 tour.???(pas, c, cpp) 可执行文件名 tour.exe 输入文件名 tour.in 输出文件名 tour.out |
【问题描述】
如今许多普通百姓家有了私家车,一些人喜爱自己驾车从一个城市到另一个城市旅游。自己驾车旅游时总会碰到加油和吃饭的问题,在出发之前,驾车人总要想方设法得到从一个城市到另一个城市路线上的加油站的列表,列表中包括了所有加油站的位置及其每升的油价(如3.25元/L)。驾车者一般都有以下的习惯:
(1)除非汽车无法用油箱里的汽油达到下一个加油站或目的地,在油箱里还有不少于最大容量一半的汽油时,驾驶员从不在加油站停下来;
(2)在第一个停下的加油站总是将油箱加满;
(3)在加油站加油的同时,买快餐等吃的东西花去20元。
(4)从起始城市出发时油箱总是满的。
(5)加油站付钱总是精确到0.1元(四舍五入)。
(6)驾车者都知道自己的汽车每升汽油能够行驶的里程数。
现在要你帮忙做的就是编写一个程序,计算出驾车从一个城市到另一个城市的旅游在加油和吃饭方面最少的费用。
【输入】
第一行是一个实数,是从出发地到目的地的距离(单位:km)。
第二行是三个实数和一个整数,其中第一个实数是汽车油箱的最大容量(单位:I。);第二个实数是汽车每升油能行驶的公里数;第三个实数是汽车在出发地加满油箱时的费用(单位元);一个整数是1到50间的数,表示从出发地到目的地线路上加油站的数目。
接下来n行都是两个实数,第一个数表示从出发地到某一个加油站的距离(单位:km);第二个实数表示该加油站汽油的价格(单位:元)。
数据项中的每个数据都是正确的,不需判错。一条线路上的加油站根据其到出发地的距离递增排列并且都不会大于从出发地到目的地的距离。
【输出】
就一个数据,是精确到0.1元的最小的加油和吃饭费用
【样例】
tour.in tour.out
600 379.6
40 8.5 128 3
200 3.52
350 3.45
500 365
【算法分析】
驾车者从出发地出发后对于每个加油站都可能有两种操作,一是进去加油买食品,二是不进去继续前行(如果当前汽车的余油可以的话),这样有n个加油站最多可能有2n种选择。由于加油站数目不太多,可以采用回溯的算法来解决问题。从第一个加油站开始,依次选择所要停下的下一个加油站,从而找出总费用最少的方案,加油站数目最多为50,这样回溯不会进行得很深。在选择下一个要停下的加油站时比较麻烦,不能完全一个一个地试过去,这样时间太长。可以用这样的方法:先找出第一个要停下的加油站,判断其后面的加油站是否可以到达,如果不可到达就必须在这里停下来加油;否则就找出可以到达但如果只用一半汽油则无法到达的所有加油站,依次进行停靠。
| 源程序名 power.???(pas, c, cpp) 可执行文件名 power.exe 输入文件名 power.in 输出文件名 power.out |
【问题描述】
某一村庄在一条路线上安装了n盏路灯,每盏灯的功率有大有小(即同一段时间内消耗的电量有多有少)。老张就住在这条路中间某一路灯旁,他有一项工作就是每天早上天亮时一盏一盏地关掉这些路灯。
为了给村里节省电费,老张记录下了每盏路灯的位置和功率,他每次关灯时也都是尽快地去关,但是老张不知道怎样去关灯才能够最节省电。他每天都是在天亮时首先关掉自己所处位置的路灯,然后可以向左也可以向右去关灯。开始他以为先算一下左边路灯的总功率再算一下右边路灯的总功率,然后选择先关掉功率大的一边,再回过头来关掉另一边的路灯,而事实并非如此,因为在关的过程中适当地调头有可能会更省一些。
现在已知老张走的速度为1m/s,每个路灯的位置(是一个整数,即距路线起点的距离,单位:m)、功率(W),老张关灯所用的时间很短而可以忽略不计。
请你为老张编一程序来安排关灯的顺序,使从老张开始关灯时刻算起所有灯消耗电最少(灯关掉后便不再消耗电了)。
【输入】
文件第一行是两个数字n(0<n<50,表示路灯的总数)和c(1<=c<=n老张所处位置的路灯号);
接下来n行,每行两个数据,表示第1盏到第n盏路灯的位置和功率。
【输出】
一个数据,即最少的功耗(单位:J,1J=1W·s)。
【样例】
power.in power.out
5 3 270 {此时关灯顺序为3 4 2 1 5,不必输出这个关灯顺序}
2 10
3 20
5 20
6 30
8 10
【算法分析】
设老张开始所在位置为c,以起始点c为分界点,算出左右两部分总的功率p_left和p_right,再来分别看向左与向右的情况。
向左走时,相应地可以减小左边应费的功,而增加右边应费的功,如果到一个点(一盏路灯处)所要时间为t,减少的功为(p_left+w[i])*t,增加的功为p_right*2t。
向右走时,相应地可以减小右边应费的功,而增加左边应费的功,如果到一个点(一盏路灯处)所要时间为t,减少的功为(p_righ+w[i])*t,增加的功为p_left*2t。
比较向左与向右的情况,找出比较好的一种确定方法。大部分情况能够解出最小值,但不能求出所有情况下最佳的解。
对于每一个所处位置,都可以选择向左或向右,不管是向左还是向右,相应耗电的变化都跟上面所述一样。所以可以选择回溯的算法来实现有限的搜索,对每一个点试探向左与向右的情况,在所有可能的情况中找出最优解。
【思考与提高】
上面的程序运算的范围很有限,当n比较大时就会栈溢出,如n>30时速度就比较慢了。实际情况调头的次数并不会多的,到底在什么时候掉头根据情况而定。我们可以从最后一步来思考:
最后一次关的可能是第一个灯也可能是最后一个灯,哪种情况所费的功小就选哪种;
最后一次关的是第一个灯的话,说明最后的方向是从最后到最前(右边到左边),最后倒数第二次的方向为从左到右,起点可能是原始起点(此时是第一趟),也可能是原始起点左边的点(此时至少是第二趟),一个个地试过去,先设拐一次弯,有可能拐的点都试过去,再试有两次拐弯换方向的情况,当再多的拐弯超过已有的解时就不要再向下试了。采用这种回溯方法,效率更高。
如果n再大一些,如到300以上,上述方法也有它的局限性,此时最好从动态规划法或贪心法的角度去思考。
第二章 递归与递推
2.1 遍历问题
| 源程序名 travel.???(pas, c, cpp) 可执行文件名 travel.exe 输入文件名 travel.in 输出文件名 travel.out |
【问题描述】
我们都很熟悉二叉树的前序、中序、后序遍历,在数据结构中常提出这样的问题:已知一棵二叉树的前序和中序遍历,求它的后序遍历,相应的,已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序遍历,你却不能确定其中序遍历序列,考虑如下图中的几棵二叉树:
a a a a
/ / \ \
b b b b
/ \ / \
c c c c
所有这些二叉树都有着相同的前序遍历和后序遍历,但中序遍历却不相同。
【输入】
输A数据共两行,第一行表示该二叉树的前序遍历结果s1,第二行表示该二叉树的后序遍历结果s2。
【输出】
输出可能的中序遍历序列的总数,结果不超过长整型数。
【样例】
trave1.in trave1.out
abc 4
bca
【算法分析】
根据二叉树先序遍历和后序遍历的特点,可以知道,先序遍历的第一个结点是后序遍历的最后一个结点,对于中序遍历来说却是中间的一个结点,这里所说的中间也只是相对而言的中间。如果一棵二叉树的根结点没有左子树,那么先序遍历的第一个结点也是中序遍历的第一个结点,如果一棵二叉树的根结点没有右子树,那么先序遍历的第一个结点是中序遍历的最后一个结点。我们这里还认为就是中序遍历的中间结点,上面两种情况只是特殊的情况。
设二叉树的结点总数为n(对于输入的字符串来说是它的长度),对于先序遍历的结果,第一个结点为根结点,从第二个结点到最后一个结点分为n种情况:
根结点的左子树结点个数为n-1,右子树结点的个数为0;
根结点的左子树结点个数为n-2,右子树结点的个数为1;
……
根结点的左子树结点个数为n-i,右子树结点的个数为i-1;{0<=i<=n-1);
……
根结点的左子树结点个数为0,右子树结点的个数为n-1。
根据这n种情况,分别将二叉树拆分为左子树和右子树,左子树结点个数为n-i,右子树结点的个数为i-l(0<=i<=n-1),先序遍历的结果是从第二个结点(字符)开始取,而后序遍历的结果里是从第1个结点字符开始取。也就是说对于每一种情况,分两步处理:第一步在先序遍历和后序遍历的结果里取左子树,看是否符合规则,统计这部分可能有的中序遍历的结果数目;第二步在先序遍历和后序遍历的结果里取右子树,看是否符合规则,统计这部分可能有的中序遍历的结果数目。这两步都递归调用了统计过程,不再递归调用的条件就是当统计的是空树或只有一个结点的树,这时返回的值是可能有的中序遍历结果数目。
结合“分类相加原理”和“分步相乘原理”,可以得到下面的递归函数:
| Function count (先序结果first,后序结果last : string) : longint; begin Len:=遍历结果的长度; 如果len为0或1,则返回结果即count:=l 否则 begin t为当前统计后符合条件的数目,初值为0; 分类统计for i:=len-1 downto 0 do begin 在first中取出长度为i的左子树结果LF; 在last中取出长度为i的左子树结果LL; 在first中取出长度为len-1-i的左子树结果RF; 在last中取出长度为len-1-i的右子树结果RL; 如果LF、LL符合基本规则(LF的首字符跟LL的尾字符相同、LF中,所有的 字符在LL中也都有) 并且RF、RL也符合基本规则,那么 t:=t+count(LF,LL)*count(RF,RL); {分步相乘、分步相加} {这里count函数中递归调用了count} end; 返回值为t即count:=t; end; end; 其中,检查先序结果和后序结果两个字符串是否符合基本规则,可以再通过一个函数来实现: function check(先序字符串F,后序字符串L):boolean; begin Check:=true; 如果F的首字符不等于L的尾字符则check:=false; 从F的第二个字符取到最后一个字符,如果该字符不在L中,则check:=false; end; |
【思考与提高】
上面的算法通过递归,结合统计的基本原理“分步相乘,分类相加”,从而统计出所有可能解的个数,如果输入的两个字符串没有解,上述算法同样能得到结果。
在肯定有解的情况下,上述算法最终可以递归调用到0、1个结点,如果有多组解,那么调用到两个结点时,如先序为ab、后序为ba,此时有可能有如下两种结构:
a a
/ \
b b
这两种结构的中序遍历结果分别为:ba、ab,有两种。
根据分步相乘的原理,对比两个字符串,每出现一次如上的情况,可能有的结构数目(结构不同,中序遍历结果也不同,因此可能有的二叉树结构的数目就是可能有的中序遍历结果数目)就乘以2一次,最终得到总的数目。这也可以理解为一种递推的方法。
从这里可以看到,在肯定有解的情况下,给定先序遍历的结果和后序遍历的结果,可能有2n种可能的结构,也就是中序遍历可能得到2n种不同的结果,其中n>=0。那么这里的n最大可能是多少呢?可以证明n的最大值为字符串的长度加1整除2。
递推的程序如下:
| Program travel(intput,output); Var Total,I,m:longint; S1,s2:string; Begin Assign(input,’travel.in’); Assign(output,’travel.out’); Reset(input); rewrite(output); Readln(s1); readln(s2); total:=1; For i:=1 to length(s1)-1 do Begin M:=pos(s1[i],s2); If m>1 then if s[i+1]=s[m-1] then total:=total*2; End; Writeln(total); close(iinput); close(output); End. |
2.2 产生数
| 源程序名 build.???(pas, c, cpp) 可执行文件名 build.exe 输入文件名 build.in 输出文件名 build.out |
【问题描述】
给出一个整数n(n<1030)和m个变换规则(m≤20)。
约定:一个数字可以变换成另一个数字,规则的右部不能为零,即零不能由另一个数字变换而成。而这里所说的一个数字就是指一个一位数。
现在给出一个整数n和m个规则,要你求出对n的每一位数字经过任意次的变换(0次或多次),能产生出多少个不同的整数。
【输入】
共m+2行,第一行是一个不超过30位的整数n,第2行是一个正整数m,接下来的m行是m个变换规则,每一规则是两个数字x、y,中间用一个空格间隔,表示x可以变换成y。
【输出】
仅一行,表示可以产生的不同整数的个数。
【样例】
build.in build.out
1 2 3 6
2
1 2
2 3
【算法分析】
如果本题用搜索,搜索的范围会很大(因为n可能有30位!),显然无法在规定的时间内出解。而我们注意到本题只需计数而不需要求出具体方案,所以我们稍加分析就会发现,可以用乘法原理直接进行计数。
设F[i]表示从数字i出发可以变换成的数字个数(这里的变换可以是直接变换,也可以是间接变换,比如样例中的1可以变换成2,而2又可以变换成3,所以1也可以变换成3;另外自己本身不变换也是一种情况)。那么对于一个长度为m位的整数a,根据乘法原理,能产生的不同的整数的个数为:F[a[1]]*F[a[2]]*F[a[3]]*…*F[a[m]]。
下面的问题是如何求F[i]呢?由于这些变换规则都是反映的数字与数字之间的关系,所以定义一个布尔型的二维数组g[0..9,0..9]来表示每对数字之间是否可以变换,初始时都为False;根据输入的数据,如果数字i能直接变换成数字j,那么g[i,j]置为True,这是通过一次变换就能得到的;接下来考虑那些间接变换可得到的数字对,很明显:如果i可以变为k,k又可以变为j,那么i就可以变为j,即:
for k:=0 to 9 do
for i:=0 to 9 do
for j:=0 to 9 do
g[i,j]=g[i,j]or(g[i,k] and g[k,j]);
最后还要注意,当n很大时,解的个数很大,所以要用高精度运算。
2.3 出栈序列统计
| 源程序名 stack.???(pas, c, cpp) 可执行文件名 stack.exe 输入文件名 stack.in 输出文件名 stack.out |
【问题描述】
栈是常用的一种数据结构,有n个元素在栈顶端一侧等待进栈,栈顶端另一侧是出栈序列。你已经知道栈的操作有两种:push和pop,前者是将一个元素进栈,后者是将栈顶元素弹出。现在要使用这两种操作,由一个操作序列可以得到一系列的输出序列。请你编程求出对于给定的n,计算并输出由操作数序列1,2,…,n,经过一系列操作可能得到的输出序列总数。
【输入】 【输出】
就一个数n(1≤n≤1000)。 一个数,即可能输出序列的总数目。
【样例】
stack.in stack.out
3 5
【算法分析】
在第一章练习里,我们通过回溯的方法计算并输出不同的出栈序列,这里只要求输出不同的出栈序列总数目,所以我们希望能找出相应的递推公式进行处理。
从排列组合的数学知识可以对此类问题加以解决。
我们先对n个元素在出栈前可能的位置进行分析,它们有n个等待进栈的位置,全部进栈后在栈里也占n个位置,也就是说n个元素在出栈前最多可能分布在2*n位置上。
出栈序列其实是从这2n个位置上选择n个位置进行组合,根据组合的原理,从2n个位置选n个,有C(2n,n)个。但是这里不同的是有许多情况是重复的,每次始终有n个连续的空位置,n个连续的空位置在2n个位置里有n+1种,所以重复了n+1次。所以出栈序列的种类数目为:
C(2n,n)/(n+1)=2n*(2n-1)*(2n-2)…*(n+1)/n!/(n+1)=2n*(2n-1)*(2n-2)*…*(n+2)/n!。
考虑到这个数据可能比较大,所以用高精度运算来计算这个结果。
本题实际是一个经典的Catalan数模型。有关Catalan数的详细解释请参考《组合数学》等书。
【思考与提高】
我们知道,在某个状态下,所能做的操作(移动方法)无非有两种:
(1)将右方的等待进栈的第一个元素进栈; (2)将栈顶的元素出栈,进入左边的出栈序列。
设此时右方、栈、左方的元素个数分别为a,b,c。我们就能用(a,b,c)表示出当前的状态。显然n=a+b+c,则c=n-a-b。即已知a和b,c就被确定,所以我们可以用(a,b)来作为状态的表示方法。则起始状态为(n,0),目标状态为(0,0)。
又由上面的两种移动方法,我们可类似的得到两种状态转移方式:
![]()
正在上传…重新上传取消
再设f(a,b)为从状态(a,b)通过移动火车变为状态(0,0)的所有移动方法。类似于动态规划的状态转移方程,我们可写出以下递归式:
![]()
正在上传…重新上传取消
边界值:f(0,0)=1。
有了这个递归公式后,再写程序就比较简单了,请读者自己写出递归程序。
2.4 计数器
| 源程序名 count.???(pas, c, cpp) 可执行文件名 count.exe 输入文件名 count.in 输出文件名 count.out |
【问题描述】
一本书的页数为N,页码从1开始编起,请你求出全部页码中,用了多少个0,1,2,…,9。其中—个页码不含多余的0,如N=1234时第5页不是0005,只是5。
【输入】
一个正整数N(N≤109),表示总的页码。
【输出】
共十行:第k行为数字k-1的个数。
【样例】
count.in count.out
11 1
4
1
1
1
1
1
1
1
1
【算法分析】
本题可以用一个循环从1到n,将其拆为一位一位的数字,并加到相应的变量里,如拆下来是1,则count[1]增加1。这种方法最简单,但当n比较大时,程序运行的时间比较长。这种方法的基本程序段如下:
for i:=1 to n do begin
j:=i;
while j>0 do begin
count[j mod 10]:=count[j mod 10]+1;
j:=j div 10;
end;
end;
当n是整型数据时,程序执行的时间不会太长。而n是长整型范围,就以n是一个9位数为例,当i执行到8位数时,每拆分一次内循环要执行8次,执行完8位数累计内循环执行的次数为:
9*1+90*2+900*3+9000*4+90000*5+900000*6+9000000*7+90000000*8
时间上让人不能忍受。
可以从连续数字本身的规律出发来进行统计,这样速度比较快,先不考虑多余的0的情况,假设从0000~9999,这一万个连续的数,0到9用到的次数都是相同的,一万个四位数,0到9这十个数字共用了40000次,每个数字使用了4000次。
进一步推广,考虑所有的n位数情况,从n个0到n个9,共10n个n位数,0到9十个数字平均使用,每个数字共用了n*10n-1次。
有了这样的规律后,可以从高位向低位进行统计,最后再减去多余的0的个数。
以n=3657为例:(用count数组来存放0到9各个数字的使用次数)
最高位(千位)为3,从0千、1千到2千,000~999重复了3次,每一次从000到999,每个基本数字都使用了3*102=300次,重复3次,所以count[0]~count[9]各增加3*300;
另外最高位的0到2作为千位又重复了1000次,count[0]~count[2]各增加1000,3作为千位用了657次(=n mod 100),因此count[3]增加657;
接下来对百位6再进行类似的处理,0到9在个位和十位平均重复使用6*20次,所以count[0]~count[9]先各增加6*20,0到5作为百位重复使用了100次,所以count[0]~count[5]再各增加100,6作为百位在这里重复用了57次(=n mod 100);因此count[6]增加57;
对十位和个位也进行相同的处理,得出count[0]~count[9]的值;
最后再减去多算的0的个数。
那么0到底多算了多少次呢?
当没有十位及以更高位时,个位的0,只多算了1次;
当没有百位及以更高位时,十位的0,多算了10次;
当没有千位及以更高位时,百位的0,多算了100次;
……
因此在统计m位数时,0多算了(11……1)这样一个全是1的m位数。
基本算法描述如下:
| 输入n; 计算n的位数Len; 将n每一位上的数字存放到数组c里; 计算10的0次方到len-1次方并存放到数组b里; i控制位数,for i:=len downto 1 do begin 0到9的使用次数增加平均使用的次数b[i-1]*(i-1)*c[i]; 0到c[i-1]的使用次数增加作为当前位使用的次数b[i-1]; c[i]的使用次数增加n mod b[i-1] end 最后减去多计算的0的个数; 输出结果。 |
2.5 诸侯安置
| 源程序名 empire.???(pas, c, cpp) 可执行文件名 empire.exe 输入文件名 empire.in 输出文件名 empire.out |
【问题描述】
很久以前,有一个强大的帝国,它的国土成正方形状,如图2—2所示。
这个国家有若干诸侯。由于这些诸侯都曾立下赫赫战功,国王准备给他们每人一块封地(正方形中的一格)。但是,这些诸侯又非常好战,当两个诸侯位于同一行或同一列时,他们就会开战。如下图2—3为n=3时的国土,阴影部分表示诸侯所处的位置。前两幅图中的诸侯可以互相攻击,第三幅则不可以。
![]()
正在上传…重新上传取消
国王自然不愿意看到他的诸侯们互相开战,致使国家动荡不安。 因此,他希望通过合理的安排诸侯所处的位置,使他们两两之间都不能攻击。
现在,给出正方形的边长n,以及需要封地的诸侯数量k,要求你求出所有可能的安置方案数。(n≤l00,k≤2n2-2n+1)
由于方案数可能很多,你只需要输出方案数除以504的余数即可。
【输入】
仅一行,两个整数n和k,中间用一空格隔开。
【输出】
一个整数,表示方案数除以504的余数。
【样例】
empire.in empire.out
2 2 4
【样例说明】
四种安置方案如图2-4所示。注意:镜面和旋转的情况属于不同的方案。
【算法分析】
重新描述一下问题,其实就是在一个边长为2n-1的正菱形(如上图2-2为n=3的情形)上摆放k个棋子,使得任意两个棋子都不在同一行、同一列。试问:这样的摆法共有多少种?
看到这道题目,我们就会立即想起一道经典的老题目:n皇后问题。这道题目与n皇后问题非常相似。但有两个不同点:一是n皇后问题可以斜着攻击对方棋子,而本题不能;二是n皇后问题是在n,n的正方形棋盘上面放置k个皇后,而本题却是在一个正菱形上摆放。我们试着先将n皇后变为不可斜攻的,再作思考,如果不能够斜着攻击,n皇后的公式是:(C(k,n))2*k!。但是本题不是一个正方形,所以这个公式对本题好像没有任何帮助。看来只能够从另外一个角度思考问题了。
首先想到在2n-1列中任意取出k列进行具体分析,这样一来问题就转化成:有一个长为k的数列(无重复元素),每一个数在一个不定的区间[a,b]当中,第i个数一定在区间[ai,bi]之间,求这样的数列有多少种?如果就是这个问题,那么比较难解决,但若把这个数列放在本题中,就比较简单。 因为题目中任意两个区间都是一种包含关系。可以先把区间按照长度排一下序,就可以看出来,再用乘法原理进行求解即可。但是,n最多可到100,k最多可到50,穷举要进行C(50,100)种方案! 显然无法在规定的时间内出解!那么怎么办呢?再继续分析一下问题发现,里面有重叠子问题。如果一个列作为最后一列,且这一列以及前面所有列共放置p个诸侯,设有q种情况,那么这一列后面的所有列共放置p+1个棋子的方案数都要用到q,从而引用乘法原理。而且在穷举过程中,这一个工作做了许多遍,所以干脆用递推。递推前,先把图形转化为类似图2-5的形式(即列排序)。
设f[i,j]表示以第i列为最后一列,放置j个棋子的总方案数,得出公式:
![]()
正在上传…重新上传取消
不过还要注意,当k≥2n-1时,问题无解。
2.6 括号序列
| 源程序名 bracket.???(pas, c, cpp) 可执行文件名 bracket.exe 输入文件名 bracket.in 输出文件名 bracket.out |
【问题描述】
定义如下规则序列(字符串):
1.空序列是规则序列;
2.如果S是规则序列,那么(S)和[S]也是规则序列;
3.如果A和B都是规则序列,那么AB也是规则序列。
例如,下面的字符串都是规则序列:
(),[],(()),([]),()[],()[()]
而以下几个则不是:
(,[,],)(,()),([()
现在,给你一些由‘(’,‘)’,‘[’,‘]’构成的序列,你要做的,是找出一个最短规则序列,使得给你的那个序列是你给出的规则序列的子列。(对于序列a1,a2,…,
![]()
正在上传…重新上传取消和序列bl,b2,…,,如果存在一组下标1≤i1<i2<…<≤m,使得aj=对一切1≤j≤n成立,那么a1,a2…,就叫做b1,b2,…,的子列。
【输入】
输入文件仅一行,全部由‘(’,‘)’,‘]’,‘]’组成,没有其他字符,长度不超过100。
【输出】
输出文件也仅有一行,全部由‘(’,‘)’,‘]’,‘]’组成,没有其他字符,把你找到的规则序列输出即可。因为规则序列可能不止一个,因此要求输出的规则序列中嵌套的层数尽可能地少。
【样例】
bracket.in bracket.out
([() ()[]() {最多的嵌套层数为1,如层数为2时的一种为()[()]}
【算法分析】
对于输入的括号序列字符串,从左向右进行查找,用一个数组来记录查找配对的情况,如果一个括号有相应的括号跟它对应,则将它标记为0,如果没有相应的括号跟它对应,则保存原子始代码的编号,“[]”分别为-1和1,“()”分别为-2和2。
因此对于读入的字符串,首先将其转换为相应的代码存放到数组里,为后面查找匹配做准备。
查找匹配时,可用这样的方法:
如果当前的字符是右括号,则跟前面的一个没有匹配的左括号对照,看是否匹配,如果匹配,则将两个字符标记为0,查找并定位到左边的第一个没有匹配的左括号(如果有的话)。如果当前的字符是左括号,则记住这个不匹配的左括号的位置,为后面找到右括号时匹配做准备。
从第一个字符开始到最后一个字符重复上面的过程,检查处理完毕。
输出时考虑到不增加嵌套的层数,以就近的原则,将出现不匹配的一个括号时,输出两个匹配的括号。
2.7 新汉诺塔
| 源程序名 hanoi.???(pas, c, cpp) 可执行文件名 hanoi.exe 输入文件名 hanoi.in 输出文件名 hanoi.out |
【问题描述】
设有n个大小不等的中空圆盘,按从小到大的顺序从1到n编号。将这n个圆盘任意的迭套在三根立柱上,立柱的编号分别为A、B、C,这个状态称为初始状态。
现在要求找到一种步数最少的移动方案,使得从初始状态转变为目标状态。
移动时有如下要求:
·一次只能移一个盘;
·不允许把大盘移到小盘上面。
【输入】
文件第一行是状态中圆盘总数;
第二到第四行分别是初始状态中A、B、C柱上圆盘的个数和从上到下每个圆盘的编号;
第五到第七行分别是目标状态中A、B、C柱上圆盘的个数和从上到下每个圆盘的编号。
【输出】
每行一步移动方案,格式为:move I from P to Q
最后一行输出最少的步数。
【样例】
Hanoi.in Hanoi.out
5 move 1 from A to B
3 3 2 1 move 2 from A to C
2 5 4 move 1 from B to C
0 move 3 from A to B
1 2 move 1 from C to B
3 5 4 3 move 2 from C to A
1 1 move 1 from B to C
7
【算法分析】
要从初始状态到目标状态.就是要把每个圆盘分别移到自己的目标状态。
怎样才能保证总的移动步数最少呢?关键是首先考虑把编号最大的圆盘移到它的目标状态,因为编号最大的圆盘移到目标位置后就不再移动了,而在编号最大的圆盘没有移到目标之前,编号小的圆盘可能还要移动,即使它已在目标状态。所以编号最大的圆盘一旦固定,对以后的移动不会造成影响。最大的移动好后,再考虑剩余的没有到达目标状态的最大号圆盘……直到最小的编号为1的圆盘到目标状态为止。
设计一个移动过程:move(k,w),表示把编号k的圆盘移到w柱。
2.8 排序集合
| 源程序名 sort.???(pas, c, cpp) 可执行文件名 sort.exe 输入文件名 sort.in 输出文件名 sort.out |
【问题描述】
对于集合N={1,2,…,n}的子集,定义一个称之为“小于”的关系:
设S1={X1,X2,…,Xi},(X1<X2<…<Xi),S2={Y1, Y2, …,Yj},(Y1<Y2<…<Yj),如果存在一个k,(0≤k≤min(i,j)),使得X1=Y1,…,Xk=Yk,且k=i或X(k+1)<Y(k+1),则称S1“小于”S2。
你的任务是,对于任意的n(n≤31)及k(k<2n),求出第k小的子集。
【输入】
输入文件仅一行,包含两个用空格隔开的自然数,n和k。
【输出】
输出文件仅一行,使该子集的元素,由小到大排列。空集输出0。
【样例】
sort.in sort.out
3 4 1 2 3
【算法分析】
我们知道,n个元素构成的集合有2n种情况。本题的意思是:把这些集合按照某种规则排序,然后输入k,输出第k个集合。所以排序的规则是本题的关键,其实很简单,当n=3时,8个集合排序如下:{}<{1}<{l,2}<{l,2,3}<{1,3}<{2}<{2,3}<{3},你发现规律了吗?具体算法为:先推出第k小的一个子集的第一个数宇是多少,第一个数字确定了之后,再推出第二个数字,从第一个数字加1一直计算累加集合个数,直到得到不超过k的最大的那个数字,就是第二位数字,这样一直递推,推到最后一个。要注意:终止条件是有了n个数字或者第i个数字为空,这时递推终止,输出最后的结果。
2.9 青蛙过河
| 源程序名 frog.???(pas, c, cpp) 可执行文件名 frog.exe 输入文件名 frog.in 输出文件名 frog.out |
【问题描述】
![]()
正在上传…重新上传取消 有一条河,左边一个石墩(A区)上有编号为1,2,3,4,…,n的n只青蛙,河中有k个荷叶(C区),还有h个石墩(D区),右边有一个石墩(B区),如下图2—5所示。n只青蛙要过河(从左岸石墩A到右岸石墩B),规则为:
(1)石墩上可以承受任意多只青蛙,荷叶只能承受一只青蛙(不论大小);
(2)青蛙可以:A→B(表示可以从A跳到B,下同),A→C,A→D,C→B,D→B,D→C,C→D;
(3)当一个石墩上有多只青蛙时,则上面的青蛙只能跳到比它大1号的青蛙上面。
你的任务是对于给出的h,k,计算并输出最多能有多少只青蛙可以根据以上规则顺利过河?
【样例】
frog.in frog.out
2 3 {河中间有2个石礅,3个荷叶} 16 {最多有16只青蛙可以按照规则过河}
【算法分析】
结论为:f(h,k)=2h(k+1)
从具体到一般,推导过程如下:
f(0,0)=1
f(0,k)=k+1; (如k=3时,有4只青蛙可以过河)
f(1,k)=2(k+1); (递推思想)
……
依此类推:f(2,k)=(2*(k+1))*2=22(k+1);
……
2.10电话号码
| 源程序名 phone.???(pas, c, cpp) 可执行文件名 phone.exe 输入文件名 phone.in 输出文件名 phone.out |
【问题描述】
电话机上每一个数字下面都写了若干个英文字母。分布如下:
1~abc
2~def
3~ghi
4~ikl
5~mn
6~opq
7~rst
8~uvw
9~xyz
现在给定一个单词表和一串数字密码,请你用单词表中的单词翻译这个密码。
【输入】
第一行为一个正整数N表示单词表中单词的个数(N≤100);
第二行为一个长度不超过100的数字串,表示密码;
接下来的N行,每行一个长度不超过20的单词,表示单词表。
【输出】
仅一行,表示翻译后的原文,如果密码无法翻译,则输出“No Solutions!”,如果密码有多种翻译方式,则输出任意一种即可。
【样例】
phone.in phone.out
8 thi shs b boo k
73373711664
thi
shs
this
is
b
a
boo
k
【算法分析】
本题可以用递归搜索求解。首先,我们注意到一个数字串对应的单词是不惟一的,而反之,一个单词所对应的数字串却是惟一的!所以,我们一开始就读入一大串的数字密码和一些可以出现的单词,我们把每一个单词所表示的密码(是惟一的)存在数组中。然后从密码的开头开始扫描,得出密码的第一个单词有可能的情况,选择其中一种,得出第一个单词,得到除第一个单词以外的后面的子密码。然后用递归实现子密码的破译。若子密码无解,就可以换一种第一个单词的取法,再次试验。如果全是无解,那整个密码也是无解的。另外,首先要判断整个密码串是否是一个单词,避免无限递归。
2.11编码
| 源程序名 encode.???(pas, c, cpp) 可执行文件名 encode.exe 输入文件名 encode.in 输出文件名 encode.out |
【问题描述】
编码工作常被运用于密文或压缩传输。这里我们用一种最简单的编码方式进行编码:把一些有规律的单词编成数宇。
字母表中共有26个字母{a,b,…,z},这些特殊的单词长度不超过6且字母按升序排列。把所有这样的单词放在一起,按字典顺序排列,一个单词的编码就对应着它在字典中的位置。
例如:
a→1 b→2 z→26 ab→27 ac→28
你的任务就是对于所给的单词,求出它的编码。
【输入】
仅一行,被编码的单词。
【输出】
仅一行,对应的编码。如果单词不在字母表中,输出0。
【样例】
encode.in encode.out
ab 27
【算法分析】
对于输入的字符串,首先检查是否符合编码的条件:全是由小写字母组成并且前面的字母不会比后面的字母大。如果符合条件则进行编码,否则输出0。
编码时如果不找规律,可以根据顺序,从第一个符合条件的单词a开始往后构造,每构造一个,相应的编码增加1,直到构造到输入的字符串。
一个单词的后序单词类似于数字的进位,如十进制中8后面是9,9后面是10——进位的情况,再如99后面是100,199后面是200。而这里单词的规则是一串中后面的字符不比前面的大,所以z后是ab,az后是bc,……两个字符的单词最大的为yz,三个字符最小的为abc,最大的为xyz,……六个字符的单词最小的为abcdef,最大的为uvwxyz。
根据上面的进位规则进行构造,构造到输入的字符串时则输出相应的序号。
由此可以写出程序。
另外可以从数学上寻找递推的规则:
一个字符的单词有26个;
两个字符的单词有:25+24+23+…+1个;
{其中ab~az共25个,bc~bz共24个,cd~cz共23个…,yz共1个}
三个字符的单词有:
(24+23+22+…+1)+(23+22+21+…+1)+…+(2+1)+(1)个
abc~ayz bcd~byz wxy~wyz xyz
四个字符的单词有:
((23+22+21+…+1)+(22+21+20+…+1)+…+(2+1)+(1))+
abcd~axyz
((22+21+20+…+1)+(21+20+…+1)+…+(2+1)+(1))+…+…+((1))个
bcde~bxyz wxyz
以此类推,得到相应的数学公式。
第三章 贪心法
3.1 排队接水
| 源程序名 water.???(pas, c, cpp) 可执行文件名 water.exe 输入文件名 water.in 输出文件名 water.out |
【问题描述】
有n个人在一个水龙头前排队接水,假如每个人接水的时间为Ti,请编程找出这n个人排队的一种顺序,使得n个人的平均等待时间最小。
【输入】
输入文件共两行,第一行为n;第二行分别表示第1个人到第n个人每人的接水时间T1,T2,…,Tn,每个数据之间有1个空格。
【输出】
输出文件有两行,第一行为一种排队顺序,即1到n的一种排列;第二行为这种排列方案下的平均等待时间(输出结果精确到小数点后两位)。
【样例】
water.in water.out
10 3 2 7 8 1 4 9 6 10 5
56 12 1 99 1000 234 33 55 99 812 291.90
【算法分析】
平均等待时间是每个人的等待时间之和再除以n,因为n是一个常数,所以等待时间之和最小,也就是平均等待时间最小。假设是按照1~n的自然顺序排列的,则这个问题就是求以下公式的最小值:
![]()
正在上传…重新上传取消
如果用穷举的方法求解,就需要我们产生n个人的所有不同排列,然后计算每种排列所需要等待的时间之和,再“打擂台”得到最小值,但这种方法需要进行n!次求和以及判断,时间复杂度很差!
其实,我们认真研究一下上面的公式,发现可以改写成如下形式:
![]()
正在上传…重新上传取消
这个公式何时取最小值呢?对于任意一种排列k1, k2, k3, …, kn,当
![]()
正在上传…重新上传取消≤≤≤…≤时,total取到最小值。如何证明呢?方法如下:
因为
![]()
正在上传…重新上传取消
假设i<j,而
![]()
正在上传…重新上传取消<,这是的和为total1,而把ki和kj互换位置,设新的和为total2,则:
![]()
正在上传…重新上传取消
我们发现上述△total恒大于0,所以也说明了任何次序的改变,都会导致等待时间的增加。从而证明了我们的设想。
既然如此,我们就得到了一种最有贪心策略:把接水时间少的人尽可能排在前面。这样一样,问题的本质就变成:把n个等待时间按非递减顺序排列,输出这种排列,并求出这种排列下的平均等待时间。
3.2 智力大冲浪
| 源程序名 riddle.???(pas, c, cpp) 可执行文件名 riddle.exe 输入文件名 riddle.in 输出文件名 riddle.out |
【问题描述】
小伟报名参加中央电视台的智力大冲浪节目。本次挑战赛吸引了众多参赛者,主持人为了表彰大家的勇气,先奖励每个参赛者m元。先不要太高兴!因为这些钱还不一定都是你的?!接下来主持人宣布了比赛规则:
首先,比赛时间分为n个时段(n≤500),它又给出了很多小游戏,每个小游戏都必须在规定期限ti前完成(1≤ti≤n)。如果一个游戏没能在规定期限前完成,则要从奖励费m元中扣去一部分钱wi,wi为自然数,不同的游戏扣去的钱是不一样的。当然,每个游戏本身都很简单,保证每个参赛者都能在一个时段内完成,而且都必须从整时段开始。主持人只是想考考每个参赛者如何安排组织自己做游戏的顺序。作为参赛者,小伟很想赢得冠军,当然更想赢取最多的钱!注意:比赛绝对不会让参赛者赔钱!
【输入】
输入文件riddle.in,共4行。
第1行为m,表示一开始奖励给每位参赛者的钱;
第2行为n,表示有n个小游戏;
第3行有n个数,分别表示游戏1到n的规定完成期限;
第4行有n个数,分别表示游戏1到n不能在规定期限前完成的扣款数。
【输出】
输出文件riddle.out,仅1行。表示小伟能赢取最多的钱。
【样例】
riddle.in riddle.out
10000 9950
7
4 2 4 3 1 4 6
70 60 50 40 30 20 10
【算法分析】
因为不同的小游戏不能准时完成时具有不同的扣款权数,而且是最优解问题,所以本题很容易就想到了贪心法。贪心的主要思想是要让扣款数值大的尽量准时完成。这样我们就先把这些任务按照扣款的数目进行排序,把大的排在前面,先进行放置。假如罚款最多的一个任务的完成期限是k,我们应该把它安排在哪个时段完成呢?应该放在第k个时段,因为放在1~k任意一个位置,效果都是一样的。一旦出现一个不可能在规定时限前完成的任务,则把其扔到最大的一个空时间段,这样必然是最优的,因为不能完成的任务,在任意一个时间段中罚款数目都是一样的,具体实现请看下面的参考程序1。
本题也可以有另外一种贪心算法,即先把所有的数据按照结束时间的先后排序,然后从前向后扫描。 当扫描到第n个时段,发现里面所分配的任务的结束时间等于n-1,那么就说明在前面这些任务中必须舍弃一个,于是再扫描第1~n这n个时段,挑出一个最小的去掉并累加扣款值,然后再去调整排列顺序,让后面的元素填补前面的空缺,具体实现请看下面的参考程序2。
3.3 取火柴游戏
| 源程序名 match.???(pas, c, cpp) 可执行文件名 match.exe 输入文件名 match.in 输出文件名 match.out |
【问题描述】
输入k及k个整数n1,n2,…,nk,表示有k堆火柴棒,第i堆火柴棒的根数为ni;接着便是你和计算机取火柴棒的对弈游戏。取的规则如下:每次可以从一堆中取走若干根火柴,也可以一堆全部取走,但不允许跨堆取,也不允许不取。
谁取走最后一根火柴为胜利者。
例如:k=2,n1=n2=2,A代表你,P代表计算机,若决定A先取:
A:(2,2)→(1,2) {从一堆中取一根}
P:(1,2)→(1,1) {从另一堆中取一根}
A:(1,1)→(1,0)
P:(1,0)→ (0,0) {P胜利}
如果决定A后取:
P:(2,2)→(2,0)
A:(2,0)→ 0,0) {A胜利}
又如k=3,n1=1,n2=2,n3=3,A决定后取:
P:(1,2,3)→(0,2,3)
A:(0,2,3)→(0,2,2)
A已将游戏归结为(2,2)的情况,不管P如何取A都必胜。
编一个程序,在给出初始状态之后,判断是先取必胜还是先取必败,如果是先取必胜,请输
出第一次该如何取。如果是先取必败,则输出“lose”。
【样例1】
match.in match.out
3 4 3 {表示第一次从第3堆取4个出来,必胜}
3 6 9 3 6 5 {第一次取后的状态}
【样例2】
match.in match.out
4 lose {先取必败}
15 22 19 10
【算法分析】
从问题的描述分析,可以将问题中的k堆火柴棒抽象为k个非负整数,而每取一次火柴棒可抽象为使其中的一个自然数变小,当所有的数都变为0时,游戏结束,最后—次取火柴棒的人为胜方。
当k较小,且k堆火柴棒也都较小时,可使用递推的方法来处理这个问题,具体做法是从终了状态(全零)反推出初始状态的值是先取必胜还是先取必败,因为某一状态的值可以从它的所有的取一次后的下一状态得到,如果某状态的所有的下一状态都为先取必败,则这一状态为先取必胜,否则为先取必败。
但当k和ni都很大时,上述方法很难行得通,为了解决这个问题,首先引进关于n个非负整数的奇偶状态的定义:如果把n个非负整数都化成二进制数,然后对n个二进制数按位相加(不进行进位),若每一位相加的结果都为偶数,则称这n个非负整数的状态为偶状态,否则称之为奇状态。可以证明:任何一个偶状态在某一个数变小后一定成为奇状态,而对任何一个奇状态,必定可以通过将某一个数的值变小,使得改变后的状态成为偶状态。前一种情况是显然的,因为一个数变小以后其对应的二进制数至少有一位发生改变。这一位的改变就破坏了原来的偶状态。后一种情况可以通过构造的方法来证明,首先对任何一个奇状态,从高位向低位寻找到第一位按位加之和为奇数的二进制位,设这一位为第k位,则n个数的对应的二进制数中至少存在一个数,其第k位为1,将这个二进制数的第k位变成0,则所有二进制数的第k位上的数字之和就变成了偶数。然后再对这个数的比k位低的所有位作如下调整:如果所有二进制数在该位按位加之和为偶数,则不改变该位的值,否则改变该数在该位的值,若原来的值为0,则改为1,若原来的值为1,则改为0,这样就构造出了一个偶状态,并且被改变的那个数一定变小了,因为这个数被改变的所有二进制位中的最高位从1变成了0。
如n=3时,三堆火柴棒的数量分别为3,6,9,则3=(0011)2,6=(0110)2,9=(1001)2,最高位之和为1,其中9对应的二进制数的最高位为1,将其变为0,次高位之和也是1,9对应的二进制数的次高位为0,根据证明过程将其变为1,最后二位数字之和均为偶数,无需作任何改变,这样9=(1001)2被变成了(0101)2=5,显然,3=(0011)2,6=(0110)2,5=(0101)2是一个偶状态。
有了前面的分析,一种贪心算法就出来了。程序中用n个包含16个元素的数组(线性表)来存放对每个非负整数对应的二进制数,如b[i, 0]存放第i个数的最低位,n个数的状态取决于它们对应的二进制数的各位数字之和的奇偶性,而各位数字之和的奇偶性只需用0和1来表示,0表示偶,1表示奇。最后的状态(全0)为偶状态,所以开始状态为偶状态时,先取必败,因为先取后局面变成了奇状态,后取方一定可将字取成偶状态,直至取光为止。反之则先取必胜。
【后记】
大家都知道国际象棋特级大师卡斯帕罗夫与IBM公司研制的“深蓝”超级计算机进行国际象棋人机大战的事吧!
有了以上算法后,我们也可以编写出这样一个游戏程序。让程序代表计算机与人做取火柴棒游戏,由人或计算机先取,要求你编的程序能够尽可能使计算机获胜。
3.4 加工生产调度
| 源程序名 prod.???(pas, c, cpp) 可执行文件名 prod.exe 输入文件名 prod.in 输出文件名 prod.out |
【问题描述】
某工厂收到了n个产品的订单,这n个产品分别在A、B两个车间加工,并且必须先在A车间加工后才可以到B车间加工。
某个产品i在A、B两车间加工的时间分别为Ai、Bi。怎样安排这n个产品的加工顺序,才能使总的加工时间最短。这里所说的加工时间是指:从开始加工第一个产品到最后所有的产品都已在A、B两车间加工完毕的时间。
【输入】
第一行仅—个数据n(0<n<1000),表示产品的数量。
接下来n个数据是表示这n个产品在A车间加工各自所要的时间(都是整数)。
最后的n个数据是表示这n个产品在B车间加工各自所要的时间(都是整数)。
【输出】
第一行一个数据,表示最少的加工时间;
第二行是一种最小加工时间的加工顺序。
【样例】
prod.in
5
3 5 8 7 10
6 2 1 4 9
prod.out
34
1 5 4 2 3
【算法分析】
本题是要求一个加工顺序使得总的加工时间最少,而要使加工时间最少,就是让各车间的空闲时间最少。一旦A车间开始加工,便会不停地进行加工(我们不要去管车间是否能够一直生产,因为他们有三班,可以24时间不停地运转)。关键是B车间在生产的过程中,有可能要等待A车间的初加工产品。很显然所安排的第一个产品在A车间加工时,B车间是要等待的,最后一个产品在B车间加工时,A车间已经完成了任务。
要使总的空闲时间最少,就要把在A车间加工时间最短的部件优先加工,这样使得B车间能以最快的速度开始加工;把放在B车间加工时间最短的产品放在最后加工,这样使得最后A车间的空闲时间最少。
设计出这样的贪心法:
设Mi=min{Ai,Bi}
将M按照由小到大的顺序排序,然后从第一个开始处理,如果Mi=Ai,则将它安排在从头开始的已经安排的生产顺序后面,如果Mi=Bi,则将它安排在从尾开始的已安排的生产顺序前面。
这种安排是否是最少的加工时间,还要通过数学证明。证明如下:
设S=<J1,J2,…,Jn),是等待加工的作业序列,如果A车间开始加工S中的产品时,B车间还在加工其他产品,t时刻后B车间就可利用A车间加工过的产品。在这样的条件下,加工S中任务所要的最短时间T(S, t)=min{Ai+T(s-{Ji},Bi+max{t-Ai, 0})},其中,Ji∈S。
图3-1是加工作业i时A车间等待B车间的情况:
![]()
正在上传…重新上传取消
图3-1 A等B的情况
图3-2是加工作业i时B车间等待A车间的情形:
![]()
正在上传…重新上传取消
图3-2 B等A的情况
假设最佳的方案中,先加工作业Ji,然后再加工作业Jj,则有:
![]()
正在上传…重新上传取消
![]()
正在上传…重新上传取消
如果
![]()
正在上传…重新上传取消,则
如果
![]()
正在上传…重新上传取消,则
如果
![]()
正在上传…重新上传取消,则
如果将作业Ji和作业Jj的加工顺序调整,则有:
![]()
正在上传…重新上传取消
其中,
![]()
正在上传…重新上传取消
按照上面的假设,有T<=T’,所以有:
![]()
正在上传…重新上传取消
从而有:
![]()
正在上传…重新上传取消
即:
![]()
转存失败重新上传取消
这说是所谓的Johnson公式,也就是说在此公式成立的条件下,优先安排任务Ji在Jj之前可以得到最优解。也就是在A车间加工时间短的安排在前面,在B车间加工时间短的任务安排在后面。
以样例数据为例:
(A1, A2, A3, A4, A5)=(3, 5, 8, 7, 10)
(B1, B2, B3, B4, B5)=(6, 2, 1, 4, 9)
则(m1, m2, m3, m4, m5)=(3, 2, 1, 4, 9)
排序之后为:(m3, m2, m1, m4, m5)
处理m3,因为m3=B3,所以m3安排在后面(,,,,3);
处理m2,因为m2=B2,所以m2安排在后面(,,,2,3);
处理m1,因为m1=A1,所以m1安排在前面(1,,,2,3);
处理m4,因为m4=B4,所以m4安排在后面(1,,4,2,3);
处理m5,因为m5=B5,所以m5安排在后面(1,5,4,2,3)。
从而得到加工的顺序1,5,4,2,3。计算出最短的加工时间34。
【补充说明】
由于本题的原始数据并没有保证数据间没有重复,所以在数据有重复的情况下生产调度安排并不是惟一的。但是最少的加工时间是惟一的。
3.5 最大乘积
| 源程序名 maxmul.???(pas, c, cpp) 可执行文件名 maxmul.exe 输入文件名 maxmul.in 输出文件名 maxmul.out |
【问题描述】
一个正整数一般可以分为几个互不相同的自然数的和,如3=1+2,4=1+3,5=1+4=2+3,6=1+5=2+4,…。
现在你的任务是将指定的正整数n分解成若干个互不相同的自然数的和,且使这些自然数的乘积最大。
【输入】
只一个正整数n,(3≤n≤10000)。
【输出】
第一行是分解方案,相邻的数之间用一个空格分开,并且按由小到大的顺序。
第二行是最大的乘积。
【样例】
maxmul.in maxmul.out
10 2 3 5
30
【算法分析】
初看此题,很容易想到用回溯法进行搜索,但是这里的n范围比较大,最多到10000,如果盲目搜索,运行时间比较长,效率很低,对于部分数据可能得到结果,对于大部分数据会超时或栈溢出。
先来看看几个n比较小的例子,看能否从中找出规律:
| n | 分解方案 | 最大的乘积 |
| 5 | 2 3 | 6 |
| 6 | 2 4 | 8 |
| 7 | 3 4 | 12 |
| 8 | 3 5 | 15 |
| 9 | 2 3 4 | 24 |
| 10 | 2 3 5 | 30 |
可以发现,将n分解成a1, a2, a3, a4,…, am这m个自然数,该序列为从2开始的一串由小到大的自然数,如果a1为1,则对乘积没有影响,而且使n减少,没有实际意义,只有特殊情况如n为3、4时才可能用上。
设h>=5,可以证明当将h拆分为两个不相同的部分并且两部分都大于1时两部分的乘积大于h。证明如下:
将h分为两部分:a,h-a其中2<=a<h/2,两部分的乘积为a*(h-a)。
a*(h-a)-h=h*a-a*a-h=h*(a-1)-a*a
因为h>2*a,所以a*(h-a)-h>2*a*(a-1)-a*a=a*a-2*a=a*(a-2)
又因为a>=2,所以a*(a-2)>=0,所以a*(h-a)-h>O即a*(h-a)>h。
从上面的证明可以看出,对于指定的正整数,如果其大于等于5,将它拆分为不同的部分后乘积变大,对于中间结果也是如此。因此可以将指定的n,依次拆成a1+a2+a3+a4+…+am,乘积最大。
现在的问题是如何拆分才能保证n=a1+a2+a3+a4+…+am呢?
可以先这样取:当和不足n时,a1取2,a2取3,…,am-1取m,即从2开始按照自然数的顺序取数,最后剩余的数给am,如果am<=am-1,此时am跟前面的数字出现了重复,则把am从后面开始平均分布给前面的m-1个数。为什么要从后面开始往前呢?同样是考虑数据不出现重复的问题,如果是从前面往后面来平均分配,如2加上1以后变成3,就跟后面的已有的3出现了重复。这样操作到底是否正确、是否能保证乘积最大呢?还要加以证明。证明过程如下:
设两个整数a,b的和为2s,且a<>b,设a=s-1,则b=s+1,a*b=(s-1)*(s+1)=s2-1,如果a=s-2,则b=s+2,a*b=(s-2)*(s+2)=s2-4。
a-b的绝对值越小,乘积的常数项越大,即乘积越大,上面的序列a1, a2, a3, a4, …, am正好满足了a-b的绝对值最小。但是还要注意两个特例就是n=3和n=4的情况,它们的分解方案分别为1,2和1,3,乘积分别为2和3。
以n=10为例,先拆分为:10=2+3+4+1,最后一项为1,比4小,将其分配给前面的一项,得到10=2+3+5,所以最大的乘积为2*3*5=30。
以n=20为例,拆分为:20=2+3+4+5+6,正好是连续自然数的和,所以最大乘积为2*3*4*5*6=720。
再以n=26为例,先拆分为:26=2+3+4+5+6+6,因为最后一项为6,不比最后第二项大,所以将其平均分给前面的项,优先考虑后面的项,即前面的4项各分到1,笫5项6分到2,最后是26=3+4+5+6+8,所以最大的乘积为3*4*5*6*8=2880。
由于n可能大到10000,分解之后的各项乘积位数比较多,超过普通的数据类型的位数,所以要用到高精度运算来进行整数的乘法运算,将结果保存在数组里。
本题的贪心策略就是:
要使乘积最大,尽可能地将指定的n(n>4)拆分成从2开始的连续的自然数的和,如果最后有剩余的数,将这个剩余的数在优先考虑后面项的情况下平均分给前面的各项。
基本算法描述如下:
| (1)拆分过程 拆分的数a先取2; 当n>a时做 Begin 选择a作为一项; a增加1; n减少a; End; 如果n>0,那么将n从最后一项开始平均分给各项; 如果n还大于0,再从最后一项开始分一次; (2)求乘积 设置一个数组来存放乘积,初始状态位数为1,结果为1; 将上面拆分的各项依次跟数组各项相乘并考虑进位; |
3.6 种树
| 源程序名 trees.???(pas, c, cpp) 可执行文件名 trees.exe 输入文件名 trees.in 输出文件名 trees.out |
【问题描述】
一条街的一边有几座房子。因为环保原因居民想要在路边种些树。路边的地区被分割成块,并被编号成1..N。每个部分为一个单位尺寸大小并最多可种一棵树。每个居民想在门前种些树并指定了三个号码B,E,T。这三个数表示该居民想在B和E之间最少种T棵树。当然,B≤E,居民必须记住在指定区不能种多于区域地块数的树,所以T≤E-B+l。居民们想种树的各自区域可以交叉。你的任务是求出能满足所有要求的最少的树的数量。
写一个程序完成以下工作:
* 从trees.in读入数据
* 计算最少要种树的数量和位置
* 把结果写到trees.out
【输入】
第一行包含数据N,区域的个数(0<N≤30000);
第二行包含H,房子的数目(0<H≤5000);
下面的H行描述居民们的需要:B E T,0<B≤E≤30000,T≤E-B+1。
【输出】
输出文件第一行写有树的数目,下面的行包括所有树的位置,相邻两数之间用一个空格隔开。
【样例】
trees.in trees.out
9 5
4 1 4 5 8 9
1 4 2
4 6 2
8 9 2
3 5 2
【算法分析】
不难想到下面的贪心算法:按照每个区间的右端点排序,从左向右扫描,把每个区间内的树都尽量种在该区间的右端,由于后一个区间的右端不在这个区间的右端的左边(排序),可以保证这些树尽可能多地被下面的区间利用到。
扫描需要的时间为O(h),更新需要的时间为O(n),所以总的时间复杂度为O(n*h)。
3.7 餐巾
| 源程序名 napkin.???(pas, c, cpp) 可执行文件名 napkin.exe 输入文件名 napkin.in 输出文件名 napkin.out |
【问题描述】
一个餐厅在相继的N天里,第i天需要Ri块餐巾(i=l,2,…,N)。餐厅可以从三种途径获得餐巾。
(1)购买新的餐巾,每块需p分;
(2)把用过的餐巾送到快洗部,洗一块需m天,费用需f分(f<p)。如m=l时,第一天送到快洗部的餐巾第二天就可以使用了,送慢洗的情况也如此。
(3)把餐巾送到慢洗部,洗一块需n天(n>m),费用需s分(s<f)。
在每天结束时,餐厅必须决定多少块用过的餐巾送到快洗部,多少块送慢洗部。在每天开始时,餐厅必须决定是否购买新餐巾及多少,使洗好的和新购的餐巾之和满足当天的需求量Ri,并使N天总的费用最小。
【输入】
输入文件共3行,第1行为总天数;第2行为每天所需的餐巾块数;第3行为每块餐巾的新购费用p,快洗所需天数m,快洗所需费用f,慢洗所需天数n,慢洗所需费用s。
【输出】
输出文件共n+1行。第1行为最小的费用。下面的n行为从第1天开始每天需要的总餐巾数、需购买的新餐巾数、结束时往快、慢洗部送洗的餐巾数以及用到的来自快洗的餐巾数和来自慢洗的餐巾数。
【样例】
napkin.in napkin.out
3 64
3 2 4 3 3 1 2 0 0
10 1 6 2 3 2 1 2 0 1 0
4 0 0 0 2 2
【算法分析】
在思考这个问题时,一般容易想到从洗的角度去思考,这就必然要对每天的餐巾来源进行分类穷举,当天数较长,每天需求量较大时,穷举的数量级至少为每天的餐巾数之积,程序很难在规定时间内运行出最优解。如果从买的角度去思考这个问题,则该问题就变得十分简单。在确定要买的餐巾数之后,显然这些餐巾购买得越早,被反复利用的可能就越大。也就是说,这些餐巾必须在最早的几天中购买,余下的缺口用洗出来的餐巾来填补,对每天用下来的餐巾,假设全部都送洗,但送洗时不确定其状态,即它们有可能被快洗,有可能被慢洗,也可能不用洗,其状态在今后被选用时再确定。在确定每天的需求时,除去买的,剩下的首先要选用慢洗为好。这种餐巾有多少应用多少,不够再选用快洗出来的餐巾。选用快洗出来的餐巾时,应选用最近的若干天中才快洗出来的餐巾,这样可以保证有更多的餐巾被慢洗出来。这就是我
们的贪心思想。
对所要购买的餐巾数进行穷举,开始时其值为所需用餐巾数之和,当购买量太少而周转不过来时,程序结束。在确定了购买的餐巾总数后,按上述算法构造出最小费用方案,所有的最小费用方案中的最优解即为问题的解。程序(见本书光盘)中数组need存放每天需用的餐巾数,数组fromslow记录每天来自慢洗的餐巾数。数组fromfast记录每天来自快洗的餐巾数,数组buy记录每天购买的餐巾数。变量restslow存储当天可供选用的已经慢洗好的餐巾数。这个算法的数量级为O(n),其中n为所有天中需用的餐巾数之总和。
3.8 马拉松接力赛
| 源程序名 marathon.???(pas, c, cpp) 可执行文件名 marathon.exe 输入文件名 marath.in 输出文件名 marath.out |
【问题描述】
某城市冬季举办环城25km马拉松接力赛,每个代表队有5人参加比赛,比赛要求每个的每名参赛选手只能跑一次,一次至少跑1km、最多只能跑10km,而且每个选手所跑的公里数必须为整数,即接力的地方在整公里处。
刘老师作为学校代表队的教练,精心选择了5名长跑能手,进行了训练和测试,得到了这5名选手尽力连续跑1km、2km、…、10km的所用时间。现在他要进行一个合理的安排,让每个选手跑合适的公里数,使学校代表队跑完25km所用的时间最短。根据队员的情况,这个最短的时间是惟一的,但安排方案可能并不惟一。
根据测试情况及一般运动员的情况得知,连续跑1km要比连续跑2km速度快,连续跑2km又要比连续跑3km速度快……也就是说连续跑的路程越长,速度越慢,当然也有特殊的,就是速度不会变慢,但是绝不可能变快。
【输入】
5行数据,分别是1到5号队员的测试数据,每行的10个整数,表示某一个运动员尽力连续跑1km、2km、…、10km所用的时间。
【输出】
两行,第一行是最短的时间,第二行是五个数据,分别是1到5号队员各自连续跑的公里数。
【样例】
marath.in marath.out
333 700 1200 1710 2240 2613 3245 3956 4778 5899 9748
300 610 960 1370 1800 2712 3834 4834 5998 7682 6 5 5 4 5
298 612 990 1560 2109 2896 3790 4747 5996 7654
289 577 890 1381 1976 2734 3876 5678 6890 9876
312 633 995 1467 1845 2634 3636 4812 5999 8123
【算法分析】
初看此题,好象是一个排列问题,选取5个10之间的数,共有10*10*10*10*10=100000种情况,对每一种情况,再看其和是否为25,在和为25的情况下再计算所用的总时间,找出其中最少的。
这种枚举的方法,肯定能找到最优解,但是这样做的效率不高,执行时间长,这里是5个选手还行,如果更多,如15个选手,就要对l015种可能情况进行判定,再快的计算机也要较长的时间来执行。
因为运动员连续跑一公里要比连续跑两公里速度快、连续跑两公里又要比连续跑三公里速度快……也就是说连续跑的路程越长,速度越慢,所以我们可以将每个选手的所跑时间进行分段处理,计算出各自所跑每一公里所用的时间。又因为要求每个选手至少跑一公里,先给每一个人分配一公里。剩下的里程由哪个选手来跑呢?这时检查各自所跑第二公里所用的时间,哪个用的时间最短就选这个选手继续跑一公里,因为这样做可以保证当前所用的时间最少,这个所手所跑的公里数增加1。下一公里继续用这种方法选,看当前要跑一公里哪个用的时间最短就选谁,选了谁,谁所跑的公里数增加l,下面要检查的时间段就是他的下一段……如此反复直到25公里分配完为止。
对于每个运动员跑各公里所用的时间不一定要单独计算出来,如它跑第5公里所用的时间等于他连续跑完5公里所用的时间减去他连续跑4公里所用的时间。
本题所用的贪心策略就是:
先分配每个运动员跑一公里;剩下的20公里始终选择所有运动员当中下一公里跑的时间最短的,直到分配完。
这样局部的最优保证整体的最优。
3.9 线性存储问题
| 源程序名 storage.???(pas, c, cpp) 可执行文件名 storage.exe 输入文件名 storage.in 输出文件名 storage.out |
【问题描述】
磁带等存储介质存储信息时基本上都是一种线性存储的方式,线性存储方式虽然简单,但查询检索时往往要经过一些其它信息,不象磁盘等存储介质在目录区找到后可直接定位到某一区城,因此线性存储总有它的局限性。但是由于磁带等线性存储有简单、保存时间相对较长等优点,现在仍然在使用。
如果有n段信息资料要线性存储在某种存储介质上,它们的长度分别是L1,L2,…,Ln,存储介质能够保存下所有这些信息,假设它们的使用(查询检索)的频率分别是F1,F2,…,Fn,要如何存储这些信息资料才能使平均检索时间最短。
你的任务就是编程安排一种平均检索时间最短的方案。
【输入】
第一行是一个正整数n(n<10000),接下来是n行数据,每行两个整数分别是第1段信息的长度(1到10000之间)和使用的频率(万分比,在0到9000之间),总的频率之和为10000。
所输入数据均不要判错。
【输出】
依次存储信息段的编号。每个数据之间用一个空格隔开。
【样例】
storage.in storage.out
5 4 1 3 5 2
10 4000
20 1000
30 1000
35 1500
12 2500
【算法分析】
根据统计的基本原理,n段信息资料的使用(查询检索)的频率之和应为1,即F1+F2+…+Fn=1,如果总的检索次数为m,第I段信息资料使用的次数为m*Fi,设平均检索速度为v单位长度/单位时间,而它的长度为Li,每次所用的时间为Ti-1+Li/V,其中Ti-1为通过安排在第I个信息段前面的所有信息所要的时间,访问信息段I所有次数总的时间时:
m*Fi*(Ti-1+Li/v)。
因为上表达式中m、v可看作是常数,所以单一访问时间Fi与Li及前面的安排有关,每段信息均是这样,由此我们可采用如下的贪心方法:
根据(频率*长度)进行由大到小的排序,然后根据这个排序安排某一信息段在相应位置,从而得到的总的检索时间最短,也就是平均检索时间最短。
3.10扇区填数
| 源程序名 fan.???(pas, c, cpp) 可执行文件名 fan.exe 输入文件名 fan.in 输出文件名 fan.out |
【问题描述】
有一个圆,当输入一个整数n(1≤n≤6)后,它被分成n个扇区,请你为每一扇区选择一个自然数(大于0的整数)。
向各个扇区放入数之后,你可以从单个扇区中选出—个数,也可以从相邻的两个或多个扇区中各选一个数,相加后形成一个新的数,请使用这些整数形成一个连续的整数序列,:1,2,3,…,i,你的任务是使i尽可能地大。
【输入】
只一个整数n(1<=n<=6)。
【输出】
第一行是最大的i,接下来的几行是所有能达到最大i的填法。
由于圆里不分顺序,所以同一种填法可以有多种输出。为了减少这种情况,这里规定从1,开始输出(因为连续数里要有1,所以所填的数中肯定有1)。
【样例】
fan.in fan.out
1 1
1
【算法分析】
假设圆已经被分成了n个扇区,并且已经在这n个扇区中填好了数字,先来看看填好数字后最多有多少种选择连续的数字并求和的方法,以N=4为例:
单独选一个,有n种即1、2、3、4;
选择相邻两个也有n种即12、23、34、41
选择相邻三个也有n种即123、234、341、412;
选择相邻四个只有一种即1234。
总共有n*(n-1)+1种,当n=4时有13种。
如果每一种选择所求的和都不同,那么能够构成的最多有n*(n-1)+1个不同的数。我们当然希望能够达到的最大的连续数就是从1到n*(n-1)+1了,如N=4时就是1到13。
现在的问题是如何保证这n*(n-1)+1个数就是从1到n*(n-1)+1。在填数时首先填1,接下来的n-1个数都保证不同且最小为2,再看其他的取相邻的多个数的情况了。在n<=6的情况下都能满足这个要求,对于n>6时就不一定了。
从这种最优策略出发,再结合回溯法找出所有可能的情况。
第四章 分治
4.1 取余运算
| 源程序名 mod.???(pas, c, cpp) 可执行文件名 mod.exe 输入文件名 mod.in 输出文件名 mod.out |
【问题描述】
输入b,p,k的值,求b p mod k的值。其中b,p,k*k为长整型数。
【样例】
mod.in mod.out
2 10 9 2^10 mod 9=7
【知识准备】
进制转换的思想、二分法。
【算法分析】
本题主要的难点在于数据规模很大(b, p都是长整型数),对于bp显然不能死算,那样的话时间复杂度和编程复杂度都很大。
下面先介绍一个原理:a*b mod k=(a mod k)*(b mod k)mod k。显然有了这个原理,就可以把较大的幂分解成较小的,因而免去高精度计算等复杂过程。那么怎样分解最有效呢?显然对于任何一个自然数P,有p=2*p div 2+p mod 2,如19=2*19 div 2十19 mod 2=2*9+1,利用上述原理就可以把b的19次方除以k的余数转换为求b的9次方除以k的余数,即b19=b2*9+1=b*b9*b9,再进一步分解下去就不难求得整个问题的解。
这是一个典型的分治问题,具体实现的时候是用递推的方法来处理的,如p=19,有19=2*9+1,9=2*4+1,4=2*2+0,2=2*1+0,1=2*0+1,反过来,我们可以从0出发,通过乘以2再加上一个0或1而推出1,2,4,9,19,这样就逐步得到了原来的指数,进而递推出以b为底,依次以这些数为指数的自然数除以k的余数。不难看出这里每一次乘以2后要加的数就是19对应的二进制数的各位数字,即1,0,0,1,1,而19=(10011)2,求解的过程也就是将二进制数还原为十进制数的过程。
具体实现请看下面的程序,程序中用数组binary存放p对应的二进制数,总位数为len,binary[1]存放最底位。变量rest记录每一步求得的余数。
4.2 地毯填补问题
| 源程序名 blank.???(pas, c, cpp) 可执行文件名 blank.exe 输入文件名 blank.in 输出文件名 blank.out |
【问题描述】
相传在一个古老的阿拉伯国家里,有一座宫殿。宫殿里有个四四方方的格子迷宫,国王选择驸马的方法非常特殊,也非常简单:公主就站在其中一个方格子上,只要谁能用地毯将除公主站立的地方外的所有地方盖上,美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住,毯子的形状有所规定,只能有四种选择(如图4-l):
(1) (2) (3) (4)
并且每一方格只能用一层地毯,迷宫的大小为(2k)2的方形。当然,也不能让公主无限制的在那儿等,对吧?由于你使用的是计算机,所以实现时间为1s。
【输入】
输入文件共2行。
第一行:k,即给定被填补迷宫的大小为2k(0<k≤10);
第二行:x y,即给出公主所在方格的坐标(x为行坐标,y为列坐标),x和y之间有一个空格隔开。
【输出】
将迷宫填补完整的方案:每一补(行)为x y c (x,y为毯子拐角的行坐标和列坐标,c为使用毯子的形状,具体见上面的图1,毯子形状分别用1、2、3、4表示,x、y、c之间用一个空格隔开)。
【样例】
blank.in blank.out
3 5 5 1
3 3 2 2 4
1 1 4
1 4 3
4 1 2
4 4 1
2 7 3
1 5 4
1 8 3
3 6 3
4 8 1
7 2 2
5 1 4
6 3 2
8 1 2
8 4 1
7 7 1
6 6 1
5 8 3
8 5 2
8 8 1
【知识准备】
分治思想和递归程序设计。
【算法分析】
拿到这个问题后,便有一种递归重复的感觉。首先对最简单的情况(即k=1)进行分析:公主只会在4个方格中的一个:
左上角:则使用3号毯子补,毯子拐角坐标位于(2, 2);{下面就简称为毯子坐标}
左下角:则使用2号毯子补,毯子拐角坐标位于(1, 2);
右上角:则使用1号毯子补,毯子拐角坐标位于(2, 1);
右下角:则使用4号毯子补,毯子拐角坐标位于(1, 1);
其实这样不能说明什么问题,但是继续讨论就会有收获,即讨论k=2的情况(如图4-1):
| # | # | # | ● |
| # | ○ | # | # |
| # | ○ | ○ | # |
| # | # | # | # |
我们假设公主所在的位置用实心圆表示,即上图中的(1, 4),那么我们就可以把1号毯子放在(2, 3)处,这样就将(1, 3)至(2, 4)的k=1见方全部覆盖(#表示地毯)。接下来就是3个k=1的见方继续填满,这样问题就归结为k=1的情况了,但是有一点不同的是:没有“公主”了,每一个k=1的小见方都会留下一个空白(即上图中的空心圆),那么空白就有:1*3=3个,组合后便又是一个地毯形状。
好了,现在有感觉了吧,我们用分治法来解决它!对于任意k>1的宫殿,均可以将其化分为4个k/2大小的宫殿,先看一下公主站的位置是属于哪一块,因为根据公主所在的位置,我们可以确定中间位置所放的毯子类型,再递归处理公主所站的那一块,直到出现边界条件k=1的情况,然后在公主边上铺上一块合适的地毯,递归结束。
由于要递归到每一格,复杂度就是面积,就是O(22*k*k)。
4.3 平面上的最接近点对
| 源程序名 nearest.???(pas, c, cpp) 可执行文件名 nearest.exe 输入文件名 nearest.in 输出文件名 nearest.out |
【问题描述】
给定平面上n个点,找出其中的一对点的距离,使得在这n个点的所有点对中,该距离为所有点对中最小的。
【输入】
第一行:n;2≤n≤60000
接下来n行:每行两个实数:x y,表示一个点的行坐标和列坐标,中间用一个空格隔开。
【输出】
仅一行,一个实数,表示最短距离,精确到小数点后面4位。
【样例】
nearest.in nearest.out
3 1.0000
1 1
1 2
2 2
【参考程序】
中位数、解析几何、时间复杂度、二分法
【算法分析】
如果n很小,那么本题很容易。我们只要将每一点对于其它n-1个点的距离算出,找出最小距离即可。时间复杂度O(n2)。但本题n很大,显然会超时。所以我们要寻找更快的解决问题的方法。我们首先想到能不能缩小计算的规模,即把n个点的问题分治成一些小规模的问题呢?
由于二维情况下的问题计算过于复杂,所以先讨论一维的情况,假设点集为S。
我们用X轴上某个点m将点集S划分为2个子集S1和S2,使得S1={x∈S|x≤m};S2={x∈S|x>m}。这样一来,对于所有p∈S1和q∈S2有p<q。
递归地在S1和S2上找出其最接近的点对{p1, p2}和{q1, q2},并设δ=MIN{|p2-p1|,|q2-q1|},S中的最接近点对或者是{p1, p2},或者是{q1, q2},或者是某个{p3, q3},其中p3∈S1且q3∈S2。如图4-2所示:
![]()
正在上传…重新上传取消
图 4-2 一维情形的分治法
我们注意到,如果S的最接近点对是{p3, q3},即|p3-q3|<δ,则p3和q3两者与m的距离不超过δ,即|p3-m|<δ,|q3-m|<δ,也就是说,p3∈(m-δ, m),q3∈(m, m+δ)。由于每个长度为δ的半闭区间至多包含S1中的一个点,并且m是S1和S2的分割点,因此(m-δ, m)中至多包含S中的一个点,则此点就是S1中的最大点。同理,如果(m-δ, m)中有S中的点,则此点就是S2中最小点。因此,我们用线性时间就可以将S1的解和S2的解合并成为S的解。也就是说,按这种分治策略,合并可在O(n)时间内完成。这样是否就可以得到一个有效算法了呢?还有一个问题有待解决,即分割点m的选择,即S1和S2的划分。选取分割点m的一个基本要求是由此导出集合S的一个线性分割,即S=S1∪S2,S1≠φ,S2≠φ,且S1∈{x|x≤m},S2∈{x|x>m}。容易看出,如果选取m=(MAX(S)+MIN(S))/2,可以满足线性分割的要求。选取分割点后,再用O(n)时间即可将S划分成S1={x∈S|x≤m}和S2={x∈S|x>m}。然而,这样选取分割点m,有可能造成划分出的子集S1和S2的不平衡。例如在最坏情况下,S1只有1个,S2有n-1个,由此产生的分治在最坏情况下所需的时间T(n)应满足递归方程:
T(n)=T(n-1)+O(n)
它的解是T(n)=O(n2)。这种效率降低的现象可以通过分治中“平衡子问题”的方法加以解决。也就是说,我们可以通过适当选择分割点m,使S1和S2中有大致相等个数的点。自然地,我们会想到用S的n个点的坐标的中位数来作分割点。这样一来,我们就能在O(n)的时间里确定m(证明略),从而得到效率相对较高的分割点。
至此,我们可以设计出一个求一维点集S中最接近点对的距离的算法:
| Function npair1(S); Begin If S中只有2个点 Then δ:=|x[2]-x[1]| Else if S中只有1个点 Then δ:=∞ Else begin M:=S中各点的坐标值的中位数; 构造S1和S2;{S1∈{x|x≤m },S2∈{x|x>m }} δ1:=npair1(S1); δ2:=npair1(S2); P:=max(S1); Q:=min(S2); δ:=min(δ1, δ2, q-p); end; Exit(δ) End; |
由以上的分析可知,该算法的分割步骤总共耗时O(n)。因此,算法耗费的计算时间T(n)满足递归方程:
T(2)=1
T(n)=2T(n/2)+O(n);
解此递归方程可得T(n)=O(n*Log2n)。
这个一维问题的算法看上去比用排序加扫描更加复杂,然而它可以推广到二维。
假设S为平面上的点集,每个点都有2个坐标值x和y。为了将点集S线性分割为大小大致相等的2个子集S1和S2,我们选取一垂直线l:x=m来作为分割直线。其中m为S中各点X坐标的中位数。由此将S分割为S1={p∈S|x(p)≤m}和S2={p∈S|x(p)>m}。从而使S1和S2分别位于直线l的左侧和右侧,且S=S1∪S2。由于m是S中各点X坐标值的中位数,因此S1和S2中的点数大致相等。
![]()
正在上传…重新上传取消 递归地在S1和S2上求解最接近点对问题,我们分别得到S1和S2中的最小距离δ1和δ2。现设δ=min(δ1, δ2)。若S的最接近点对(p, q)之间的距离d(p, q)<δ,则p和q必分属于S1和S2。不妨设p∈S1,q∈S2。那么,p和q距直线L的距离均小于δ。 因此,我们若用P1和P2分别表示直线L的左边和右边的宽为δ的2个垂直长条,则p∈P1且q∈P2,如图4-3所示:
据直线L的距离小于δ的所有点
在一维的情形下,距分割点距离为δ的2个区间(m-δ, m),(m, m+δ)中最多各有S中一个点,因而这2点成为惟一的未检查过的最接近点对候选者。二维的情形则要复杂一些,此时,P1中所有点与P2中所有点构成的点对均为最接近点对的候选者。在最坏情况下有
![]()
正在上传…重新上传取消对这样的候选者。但是P1和P2中的点具有以下的稀疏性质,它使我们不必检查所有这对候选者。考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者,则必有d(p, q)<δ。满足这个条件的P2中的点有多少个呢?容易看出这样的点一定落在一个δ*2δ的矩形R中(如图4-4所示)。
由δ的意义可知,P2中任何2个S中的点的距离都不小于δ。由此而来可以推出矩形R中最多只有6个δ/2*2/3*δ的矩形(如图4-5所示)。
![]()
正在上传…重新上传取消
图 4-4 包含点q的δ*2δ矩形R 图 4-5 图4-6
若矩形R中有多于6个S中的点,则由鸽笼原理易知至少有一个δ/2*2/3*δ的小矩形中有2个以上S中的点。设U,V是这样2个点,它们位于同一小矩形中,则:
![]()
正在上传…重新上传取消≤
因此,
![]()
正在上传…重新上传取消≤。这与δ的意义相矛盾。也就是说矩形R中最多只有6个S中的点。
图4-6是矩形R中含有S中的6个点的极端情形。由于这种稀疏性质,对于P1中任一点p,P2中最多只有6个点与它构成最接近点对的候选者。因此,在分治的合并步骤中,我们最多需要检查
![]()
正在上传…重新上传取消对候选者,而不是对候选者。这是否就意味着我们可以在O(n)时间内完成分治法的合并步骤呢?现在还不能确定,因为我们还不知道要检查哪6个点。为了解决这个问题,我们可以将p和P2中所有S2的点投影到垂线L上。由于能与p点一起构成最接近点对候选者的S2中点一定在矩形R中,所以它们在直线L上的投影距p在L上投影点的距离小于δ。由上面的分析可知,这种投影点最多只有6个。因此,若将P1和P2中所有S的点按其Y坐标排好序,则对P1中所有点,对排好序的点列作一次扫描,就可以找出所有最接近点对的候选者,对P1中每一点最多只要检查P2中排好序的相继6个点。
至此,我们得出用分治法求二维最接近点对距离的算法:
| Function npair(s); Begin If S中只有2个点 Then δ:=S中这2点的距离 Else if S中只有1个点 Then δ:=∞ Else begin (1)m:=S中各点X坐标值的中位数; 构造S1和S2; (2)δ1:=npair1(S1); δ2:=npair1(S2); (3)δm:=min(δ1, δ2); (4)设P1是S1中距垂直分割线L的距离在δm之间的所有点组成的集合, P2是S2中距分割线L的距离在δm之间的所有点组成的集合。将P1 和P2中的点依其Y坐标值从小到大排序,并设P1*和P2*是相应的已 排好序的点列; (5)通过扫描P1*,对于P1*中每个点检查P2*中与其距离在δm之内的所 有点(最多6个)可以完成合并。当P1*中的扫描指针可在宽为2*δm 的一个区间内移动。设δ1是按这种扫描方式找到的点对间的最小距 离; (6)δ:=min(δm, δt); end; Exit(δ) End; |
下面我们来分析上述算法的时间复杂性。设对于n个点的平面点集S,在(1)和(5)步用了O(n)时间,(3)和(6)用的是常数时间,(2)则用了
![]()
正在上传…重新上传取消时间,而在(4),最坏情况要O(nlog2n)时间,仍然无法承受,所以我们在整个程序的开始时,就先将S中的点对按Y座标值排序,这样一来(4)和(5)两步的时间就只需O(n)的时间了,所以总的计算时间同样满足:
T(2)=1,
![]()
正在上传…重新上传取消
由此,该问题的时间复杂度为O(nlog2n),在渐进的意义下为最优算法了。空间复杂度为O(n)。
4.4 求方程的根
| 源程序名 equation.???(pas, c, cpp) 可执行文件名 equation.exe 输入文件名 equation.in 输出文件名 equation.out |
【问题描述】
输入m,n,p,a,b,求方程f(x)=mx+nx-px=0在[a,b]内的根。m,n,p,a,b均为整数,且a<b;m,n,p都大于等于1。如果有根,则输出,精确到1E-11;如果无方程根,则输出“NO”。
【样例】
equation.in equation.out
2 3 4 1 2 1.5071265916E+00
2.9103830457E-11
【算法分析】
首先这是一个单调递增函数,对于一个单调递增(或递减)函数,如图4-7所示,判断在[a, b]范围内是否有解,解是多少。方法有多种,常用的一种方法叫“迭代法”,也就是“二分法”。先判断f(a)·f(b)≤0,如果满足则说明在[a, b]范围内有解,否则无解。如果有解再判断x=(a+b)/2是不是解,如果是则输出解结束程序,否则我们采用二分法,将范围缩小到[a, x)或(x, b],究竟在哪一半区间里有解,则要看是f(a)·f(x)<0还是f(x)·f(b)<0。
![]()
正在上传…重新上传取消
当然对于yx,我们需要用换底公式把它换成exp(xln(y))。
4.5 小车问题
| 源程序名 car.???(pas, c, cpp) 可执行文件名 car.exe 输入文件名 car.in 输出文件名 car.out |
【问题描述】
甲、乙两人同时从A地出发要尽快同时赶到B地。出发时A地有一辆小车,可是这辆小车除了驾驶员外只能带一人。已知甲、乙两人的步行速度一样,且小于车的速度。问:怎样利用小车才能使两人尽快同时到达。
【输入】
仅一行,三个数据分别表示AB两地的距离s,人的步行速度a,车的速度b。
【输出】
两人同时到达B地需要的最短时间。
【样例】
car.in car.out
120 5 25 9.6000000000E+00
【算法分析】
最佳方案为:甲先乘车到达K处后下车步行,小车再回头接已走到C处的乙,在D处相遇后,乙再乘车赶往B,最后甲、乙一起到达B地。这样问题就转换成了求K处的位置,我们用二分法,不断尝试,直到满足同时到达的时间精度。算法框架如下:
(1)输入s,a,b;
(2)c0:=0;c1:=s;c:=(c0+c1)/2;
(3)求t1,t2;
(4)如果t1<t2,那么c:=(c0+c)/2
否则c:=(c+c1)/2;
反复执行(3)和(4),直到abs(t1-t2)满足精度要求(即小于误差标准)。
4.6 黑白棋子的移动
| 源程序名 chessman.???(pas, c, cpp) 可执行文件名 chessman.exe 输入文件名 chessman.in 输出文件名 chessman.out |
【问题描述】
有2n个棋子(n≥4)排成一行,开始为位置白子全部在左边,黑子全部在右边,如下图为n=5的情况:
○○○○○●●●●●
移动棋子的规则是:每次必须同时移动相邻的两个棋子,颜色不限,可以左移也可以右移到空位上去,但不能调换两个棋子的左右位置。每次移动必须跳过若干个棋子(不能平移),要求最后能移成黑白相间的一行棋子。如n=5时,成为:
○●○●○●○●○●
任务:编程打印出移动过程。
【样例】
chessman.in chessman.out
7 step 0:ooooooo*******--
step 1:oooooo--******o*
step 2:oooooo--******o*
step 3:ooooo--*****o*o*
step 4:ooooo*****--o*o*
step 5:oooo--****o*o*o*
step 6:oooo****--o*o*o*
step 7:ooo--***o*o*o*o*
step 8:ooo*o**--*o*o*o*
step 9:o--*o**oo*o*o*o*
step 10:o*o*o*--o*o*o*o*
step 11:--o*o*o*o*o*o*o*
【问题分析】
我们先从n=4开始试试看,初始时:
○○○○●●●●
第1步:○○○——●●●○●(—表示空位)
第2步:○○○●○●●——●
第3步:○——●○●●○○●
第4步:○●○●○●——○●
第5步:——○●○●○●○●
如果n=5呢?我们继续尝试,希望看出一些规律,初始时:
○○○○○●●●●●
第1步:○○○○——●●●●○●
第2步:○○○○●●●●——○●
这样,n=5的问题又分解成了n=4的情况,下面只要再做一下n=4的5个步骤就行了。同理,n=6的情况又可以分解成n=5的情况,……,所以,对于一个规模为n的问题,我们很容易地就把它分治成了规模为n-1的相同类型子问题。
数据结构如下:数组c[1..max]用来作为棋子移动的场所,初始时,c[1]~c[n]存放白子(用字符o表示),c[n+1]~c[2n]存放黑子(用字符*表示),c[2n+1],c[2n+2]为空位置(用字符—表示)。最后结果在c[3]~c[2n+2]中。
4.7 麦森数(NOIP2003)
| 源程序名 mason.???(pas, c, cpp) 可执行文件名 mason.exe 输入文件名 mason.in 输出文件名 mason.out |
【问题描述】
形如2p-1的素数称为麦森数,这时P一定也是个素数。但反过来不一定,即如果P是个素数,2p-1不一定也是素数。到1998年底,人们已找到了37个麦森数。最大的一个是P=3021377,它有909526位。麦森数有许多重要应用,它与完全数密切相关。
任务:从文件中输入P(1000<P<3100000),计算2p-1的位数和最后500位数字(用十进制高精度数表示)。
【输入】
文件中只包含一个整数P(1000<P<3100000)。
【输出】
第一行:十进制高精度数2p-1的位数;
第2~11行:十进制高精度数2p-1的最后500位数字(每行输出50位,共输出10行,不足500位时高位补0);
不必验证2p-1与P是否为素数。
【样例】
mason.in
1279
mason.out
386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087
【问题分析】
本题的解题方法很多,其中分治也是一种巧妙的方法。首先可以想到:2n=(2 n div 2)2*2 n mod 2 ,即:如果要计算2n,就要先算出2 n div 2,然后用高精度乘法算它的平方,如果n是奇数还要再乘以2,写成递归公式就是:f(n)=(f(n div 2))2*2(n mod 2)。
当然,递归是要有边界值的,这就是当n=0时,f(n)=1。还要补充一点,该数的长度是可以用公式计算的,所以在做高精度乘法时,只要取最后500位运算就行了。
4.8 旅行家的预算(NOIP1999)
| 源程序名 trip.???(pas, c, cpp) 可执行文件名 trip.exe 输入文件名 trip.in 输出文件名 trip.out |
【问题描述】
一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市(假设出发时油箱是空的)。给定两个城市之间的距离D1、汽车油箱的容量C(以升为单位)、每升汽油能行驶的距离D2、出发点每升汽油价格P和沿途油站数N(N可以为零),油站i离出发点的距离Di、每升汽油价格Pi(i=1,2,…,N)。计算结果四舍五入至小数点后两位。如果无法到达目的地,则输出“No Solution”。
【样例】
trip.in
275.6 11.9 27.4 2.8 2 (分别表示D1,C,D2,P,N)
102.0 2.9 (以下共N行,分别表示油站i离出发点的距离Di和每升汽油价格Pi)
220.0 2.2
trip.out
26.95(该数据表示最小费用)
【问题分析】
看到这道题,许多人都马上判断出穷举是不可行的,因为数据都是以实数的形式给出的。但是,不用穷举,有什么更好的方法呢?比较容易想到的是分治法。
首先找到(从后向前)油价最低的加油站,显然车至该站油箱应为空,这样就可将起点至该站与该站至终点作为两段独立考虑,分别求其最小费用,二者之和即为总费用,这样一直分下去,若某段只有起点与终点两个加油站时无需再分,如某一段油价最低的加油站即为起点,则如能一次加油即到达该段终点则最好,若不能,则加满油再考虑油箱有油情况下的二分法,考虑起点之外所有的加油站中从后往前油价最低的加油站,若该加油站位于起点加满油后不能到达之处,则到达该站时油箱应该为空,以该站为界将全程分为两个独立段考虑,前半段为有油情况,后半段为无油情况。第二种情况,若该加油站处于起点加满油后能到达之处,则将该段总路程缩短为该加油站至终点的情况,该加油站在该段路程中最便宜,若从该站加满油仍不能到达终点,则继续分治即可。
程序被设计成一个递归函数money,形式参数start表示起点站,形式参数stop表示终点站,形式参数rest表示到达加油站start时汽车油箱余下的油的容量,money函数最终计算出从加油站start到stop区间内的最小费用,细节详见光盘所附程序清单和注释。
4.9 飞行计划
| 源程序名 trgovac.???(pas, c, cpp) 可执行文件名 trgovac.exe |
【问题描述】
16岁那年,Mirko从大学毕业当起了推销员。他必须访问N个城市一次且仅一次,为他的产品做广告。像所有的推销员一样,他将乘坐飞机来往于城市之间。
每两个城市之间有且仅有一条航线,而且总是花费1小时的时间。飞机一刻不停地沿着航线飞行。飞机的起飞时间总是在整点,例如,飞机中午从城市A起飞,飞向城市B,那么它将在下午1点在城市B降落,然后立即返回城市A,再次到达城市A的时间应该是下午2点。
Mirko想作一个计划,使得他可以在沿途的每个城市(不包括起点和终点)花上一小时做广告,然后立即前往下一个城市。换句话说,他想把N个城市排成一个序列g1,…,gn,对于每个i(1<i<n),Mirko可以在到达gi一小时后从gi出发到gi+1。Mirko可以在任何时候从g1出发(但要是整点)。
可惜的是,Mirko没有飞机时刻表,所以他不得不打电话询问航空公司。每次打电话,Mirko将选择两个不同的城市A和B,电话的那头会告诉他中午起飞的AB之间的航班是从A到B还是从B到A。打电话是要付电话费的,所以如果Mirko不想在打电话上花太多的钞票,就必须足够地聪明了。
另外,接电话的有可能是航空公司的老板。如果是他的话,他就会和Mirko开玩笑,使得Mirko尽可能多地打电话。为了开玩笑,他就不见得会按照时刻表上写的回答Mirko了。他会重新安排航班的路线,尽量让Mirko花最多的钱打电话。但是,如果接电话的是普通的职员,他会如实地回答Mirko。第一个接电话的人,以后也将一直接电话。
请你写一个程序帮助Mirko作计划。
【库】
这是一道交互式问题,你的程序必须和库trg_lib进行交互。库trg_lib中含有三个函数或过程。
Init——只能在程序开始时调用一次。返回城市的数目n,城市编号从1到n。
Function init:integer;
Int init(void);
Pitaj——打电话的过程。对于一对不同的城市A和B,如果中午的航班从A到B则返回A,否则返回B。如果pitaj(A,B)=A,则pitaj(B,A)=A。
Function pitaj(a:integer; b:integer):integer;
Int pitaj(int a,int b);
Gotovo——调用这个过程输出你的计划。Raspored[i]表示题目中说的gi。调用完这个过程之后,你的程序会自动结束。
Procedure gotovo(raspored:array of integer);
Void gotovo(int raspored[]);
【对使用PascaI的选手】
在程序开头加上uses trg_lib
【对使用C或C++的选手】
在程序开头加上#include “trg_lib.h”
最多会有900座城市,你的程序最多只能打10000次电话。
【如何测试自己的程序】
给你的库只包含普通职员的功能。Trgovac.in里面包含所有问题的答案。第一行包含城市的数目,第i+1行是pitag(i,j)的答案(j=i+1,i+2,…,n)。相邻的数用空格隔开。
例子:
5
1 1 1 5
3 4 5
3 5
5
你的程序结束后,库会建立两个新文件:trgovac.log包含交互的具体情况;trgovac.out包含打电话的次数,和你的程序返回的最终计划。如果你打电话的次数太多,文件只包含-1;如果问的问题不合法,文件只包含-2。
【注释】
一半的测试数据是普通职员回答的,另一半是精神错乱的老板回答的。
【问题分析】
本题我们可以采用二分法求解。具体分析如下:
对于已知的一条链和一个点,有以下3种情况:
1、*-->[]-->[]-->[]
2、[]-->[]-->[]-->*
3、---------->*-------->
| |
| |
[]-->[]-->[]-->[]-->[]
第1、第2种情况很好解决,第3种情况采用二分法:
---------->*-------->
| | |
| | |
[Be]——>[]——>[Mid]——>[]——>[En]
可以考虑*和mid的关系,if *-->mid then En:=mid else Be:=mid;这样,最后必然会出现这样的情况:
---->*---->
| |
| |
[Be]-->[En]
直接走上面的路径就可以了。总的提问次数为n*log2n。
第五章 图
| 源程序名 hospital.???(pas, c, cpp) 可执行文件名 hospital.exe 输入文件名 hospital.in 输出文件名 hospital.out |
【问题描述】
设有一棵二叉树,如图5-1:
131
/ \
24 123
/ \
420 405
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为l。如上图中,若医院建在:
【输入】
第一行一个整数n,表示树的结点数。(n≤100)
接下来的n行每行描述了一个结点的状况,包含三个整数,整数之间用空格(一个或多个)分隔,其中:第一个数为居民人口数;第二个数为左链接,为0表示无链接;第三个数为右链接。
【输出】
一个整数,表示最小距离和。
【样例】
hospital.in hospital.out
5 81
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
【知识准备】
图的遍历和最短路径。
【算法分析】
本题的求解任务十分明了:求一个最小路径之和。
根据题意,对n个结点,共有n个路径之和:用记号Si表示通向结点i的路径之和,则
![]()
正在上传…重新上传取消,其中Wj为结点j的居民数,g(i,j)为结点j到结点i的最短路径长度。下面表中反映的是样例的各项数据:
|
正在上传…重新上传取消j
正在上传…重新上传取消g(i,j) i | 1 | 2 | 3 | 4 | 5 | Si |
| 1 | 0 | 1 | 1 | 2 | 2 | 0×13+1×4+1×12+2×20+2×40=136 |
| 2 | 1 | 0 | 2 | 3 | 3 | 1×13+0×4+2×12+3×20+3×40=217 |
| 3 | 1 | 2 | 0 | 1 | 1 | 1×13+2×4+0×12+1×20+1×40=81 |
| 4 | 2 | 3 | 1 | 0 | 2 | 2×13+3×4+1×12+0×20+2×40=130 |
| 5 | 2 | 3 | 1 | 2 | 0 | 2×13+3×4+1×12+2×20+0×40=90 |
从表中可知S3=81最小,医院应建在3号居民点,使得所有居民走的路径之和为最小。
由此可知,本题的关键是求g[i,j],即图中任意两点间的最短路径长度。
求任意两点间的最短路径采用下面的弗洛伊德(Floyd)算法。
(1)数据结构:
w:array[1..100]of longing; 描述个居民点人口数
g:array[1..100, 1..100]of longint 初值为图的邻接矩阵,最终为最短路径长度
(2)数据的读入:
本题数据结构的原形为二叉树,数据提供为孩子标识法,分支长度为1,建立带权图的邻接矩阵,分下面两步:
①g[i,j]←Max {Max为一较大数,表示结点i与j之间无直接相连边}
②读入n个结点信息:
for i:=1 to n do
begin
g[i,j]:=0;
readln(w[i],l,r);
if l>0 then begin
g[i,l]:=l; g[l,i]:=l
end;
if r>0 then begin
g[i,r]:=l; g[r,i]:=l
end;
(3)弗洛伊德算法求任意两点间的最短路径长度
for k:=1 to n do
for i:=1 to n do
if i<>k then for j:=1 to n do
if (i<>j)and(k<>j)and(g[i,k]+g[k,j]<g[i,j]) then g[i,j]:=g[i,k]+g[k,j];
(4)求最小的路程和min
min:=max longint;
for i:=1 to n do
begin
sum:=0;
for j:=1 to n do sum:=sum+w[i]*g[i,j];
if sum<min then min:=sum;
end;
(5)输出
writeln(min);
| 源程序名 work.???(pas, c, cpp) 可执行文件名 work.exe 输入文件名 work.in 输出文件名 work.out |
【问题描述】
造一幢大楼是一项艰巨的工程,它是由n个子任务构成的,给它们分别编号1,2,…,n(5≤n≤1000)。由于对一些任务的起始条件有着严格的限制,所以每个任务的起始时间T1,T2,…,Tn并不是很容易确定的(但这些起始时间都是非负整数,因为它们必须在整个工程开始后启动)。例如:挖掘完成后,紧接着就要打地基;但是混凝土浇筑完成后,却要等待一段时间再去掉模板。
这种要求就可以用M(5≤m≤5000)个不等式表示,不等式形如Ti-Tj≤b代表i和j的起始时间必须满足的条件。每个不等式的右边都是一个常数b,这些常数可能不相同,但是它们都在区间(-100,100)内。
你的任务就是写一个程序,给定像上面那样的不等式,找出一种可能的起始时间序列T1,T2,…,Tn,或者判断问题无解。对于有解的情况,要使最早进行的那个任务和整个工程的起始时间相同,也就是说,T1,T2,…,Tn中至少有一个为0。
【输入】
第一行是用空格隔开的两个正整数n和m,下面的m行每行有三个用空格隔开的整数i,j,b对应着不等式Ti-Tj≤b。
【输出】
如果有可行的方案,那么输出N行,每行都有一个非负整数且至少有一个为0,按顺序表示每个任务的起始时间。如果没有可行的方案,就输出信息“NO SOLUTION”。
【样例1】
work.in work.out
5 8 0
1 2 0 2
1 5 –1 5
2 5 1 4
3 1 5 1
4 1 4
4 3 –1
5 3 –1
5 4 –3
【样例2】
work.in work.out
5 5 NO SOLUTION
1 2 –3
1 5 –1
2 5 –1
5 1 –5
4 1 4
【算法分析】
本题是一类称为约束满足问题的典型问题,问题描述成n个子任务的起始时间Ti及它们之间在取值上的约束,求一种满足所有约束的取值方法。
将工程的n个子任务1,2,…,n作为一有向图G的n个顶点,顶点Vi(i=1,…,n)的关键值为子任务i的起始时间Ti,我们并不需要关心顶点之间的弧及其弧长,而是要确定顶点的关键值Ti的取值,满足所有的约束条件。本题的约束条件由m个不等式Ti-Tj≤b给出,这样的有向图称为约束图。
为了确定每一个Ti的值,先假设某一个子任务的起始时间为零,如设Tj=0,则其余子任务的起始时间Ti相对于T1可设置其起始时间为一区间[-maxt,maxt]。
下面分析不等式Ti-Tj≤b。此不等式可变形为如下两种形式:
(1)Ti≤Tj+b意味Ti的最大值为Tj+b;
(2)Tj≥Ti-b意味Tj的最大值为Ti-b;
因此,根据题中给出的m个不等式,逐步调整各个Ti的最小值和最大值。
设high[i]为Ti当前的最大值,low[i]为Ti当前的最小值。
high[j]为Tj当前的最大值,low[j]为Tj当前的最小值。
若high[i]-high[j]>b,则high[i]=high[j]+b(根据Ti≤Tj+b),
若low[i]-low[j]<b,则low[j]=low[i]-b(根据Ti≥Ti-b)。
以上的调整终止视下列两种情况而定:
(1)对所有的不等式Ti-Tj≤b,不再有high[i]或low[j]的调整;
(2)若存在high[i]<low[i]或high[j]<low[j]则表示不存在T1,T2,…,Tn能满足所有m个不等式Ti-Tj≤b,即问题无解。
根据以上思路,先建立约束图,每个结点代表一个起始时间值,并记录其可能的取值范围:
数组high,low:array[1..maxn]of longint;{n个子任务起始时间的取值范围}
high[1]=0; low[1]=0; {设置n个起始时间的初值,其中Ti=0}
for i:=2 to n do begin
high[i]:=maxt; {Ti的上界}
low[i]:=-maxt; {Tj的下界}
end;
约束条件(m个不等式)用记录数组表示:
type {不等式结构}
Tinequ=record
i,j,b:longint;
end;
var
arrinequ:array[1..maxm]of Tinequ; {存放m个不等式}
利用约束条件,逐一调整每一个起始时间的取值范围,直到无法调整为止。
主要算法如下:
| flag:=true; {调整状态标记} noans:=false; {解的有无标记} while (flag) do {进行约束传递,根据不等式调整各个起始时间值} begin flag:=false; for k:=1 to m do with arrinequ[k] do begin if (high[i]-high[j]>b) then begin high[i]:=high[j]+b; flag:=true; end; {调整Ti的上界} if (low[i]-low[j]>b) then begin low[j]:=low[i]-b; flag:=true; end; {调整Tj的下界} if (low[i]>high[i]) or (low[j]>high[j]) then begin {无法满足当前不等式,则调整终止} noans:=true; {问题无解noans=true} flag:=false; break; end; end; end; |
下面以样例说明:
【样例1】
8个不等式如下
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| i | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 5 |
| j | 2 | 5 | 5 | 1 | 1 | 3 | 3 | 4 |
| b | 0 | -1 | 1 | 5 | 4 | -1 | -3 | -3 |
顶点的关键值Ti的调整记录:
| 初值 | 第1轮调整 | 第2轮调整 | 第3轮调整 | |
| high[1] | 0 | 0 | 0 | 0 |
| low[1] | 0 | 0 | 0 | 0 |
| high[2] | 100000 | 100000 | 2 | 2 |
| low[2] | -10000 | 2 | 2 | 2 |
| high[3] | 100000 | 5 | 5 | 5 |
| low[3] | -10000 | 4 | 5 | 5 |
| high[4] | 100000 | 4 | 4 | 4 |
| low[4] | -10000 | 4 | 4 | 4 |
| high[5] | 100000 | 1 | 1 | 1 |
| low[5] | -10000 | 1 | 1 | 1 |
| 调整状态 | 有变化 | 有变化 | 无变化 | |
【样例2】
5个不等式如下
| 编号 | 1 | 2 | 3 | 4 | 5 |
| i | 1 | 1 | 2 | 5 | 4 |
| j | 2 | 5 | 5 | 1 | 1 |
| b | -3 | -1 | -1 | -5 | 4 |
顶点关键值Ti的调整记录:
| 初值 | 第一轮调整 | 第二轮调整 | ||
| 1 | high | 0 | 0 | |
| low | 0 | 0 | ||
| 2 | high | 100000 | 99999 | |
| low | -10000 | 3 | ||
| 3 | high | 100000 | 10000 | |
| low | -10000 | -10000 | ||
| 4 | high | 100000 | 4 | |
| low | -10000 | -10000 | ||
| 5 | high | 100000 | -5 | |
| low | -10000 | 1 | ||
| 调整情况 | high[5]<low[5]终止 | |||
经第一轮调整,调整过程终止,即问题无解。
从样例2所给不等式也可看出,因为:
T1-T2≤-3,→T2>T1
T2-T5≤-1,→T5>T2
T5-T1≤-5,→T1>T5
这三个不等式不能同时成立,因此问题无解。
| 源程序名 servers.???(pas, c, cpp) 可执行文件名 servers.exe 输入文件名 servers.in 输出文件名 servers.out |
【问题描述】
Byteland王国准备在各服务器间建立大型网络并提供多种服务。
网络由n台服务器组成,用双向的线连接。两台服务器之间最多只能有一条线直接连接,同时,每台服务器最多只能和10台服务器直接连接,但是任意两台服务器间必然存在一条路径将它们连接在一起。每条传输线都有一个固定传输的速度。δ(V, W)表示服务器V和W之间的最短路径长度,且对任意的V有δ(V, V)=0。
有些服务器比别的服务器提供更多的服务,它们的重要程度要高一些。我们用r(V)表示服务器V的重要程度(rank)。rank越高的服务器越重要。
每台服务器都会存储它附近的服务器的信息。当然,不是所有服务器的信息都存,只有感兴趣的服务器信息才会被存储。服务器V对服务器W感兴趣是指,不存在服务器U满足,r(U)>r(W)且δ(V, U)<δ(V, W)。
举个例子来说,所有具有最高rank的服务器都会被别的服务器感兴趣。如果V是一台具有最高rank的服务器,由于δ(V, V)=0,所以V只对具有最高rank的服务器感兴趣。我们定义B(V)为V感兴趣的服务器的集合。
我们希望计算所有服务器储存的信息量,即所有服务器的|B(V)|之和。Byteland王国并不希望存储大量的数据,所以所有服务器存储的数据量(|B(V)|之和)不会超过30n。
你的任务是写一个程序,读入Byteland王国的网络分布,计算所有服务器存储的数据量。
【输入】
第一行两个整数n和m,(1≤n≤30000,1≤m≤5n)。n表示服务器的数量,m表示传输线的数量。
接下来n行,每行一个整数,第i行的整数为r(i)(1≤r(i)≤10),表示第i台服务器的rank。
接下来m行,每行表示各条传输线的信息,包含三个整数a,b,t(1≤t≤1000,1≤a,b≤n,a≠b)。a和b是传榆线所连接的两台服务器的编号,t是传输线的长度。
【输出】
一个整数,表示所有服务器存储的数据总量,即|B(V)|之和。
【样例】
servers.in servers.out
4 3 9
2
3
1
1
1 4 30
2 3 20
3 4 20
注:B(1)={1,2},B(2)={2},B(3)={2,3},B(4)={1,2,3,4}。
【知识准备】
Dijkstra算法,及其O((n+e)log2n)或O(nlog2n+e)的实现。
【算法分析】
本题的难点在于问题的规模。如果问题的规模在100左右,那么这将是一道非常容易的题目。因为O(n3)的算法是很容易想到的:
(1)求出任意两点间的最短路径,时间复杂度为O(n3);
(2)枚举任意两点,根据定义判断一个节点是否对另一个节点感兴趣,时间复杂度为O(n3)。
当然,对于30000规模的本题来说,O(n3)的算法是绝对不可行的,即便降到O(n2)也不行,只有O(nlog2n)或O(n)是可以接受的。
既然现在可以得到的算法与要求相去甚远,要想一鼓作气得到一个可行的算法似乎就不是那么容易了。我们不妨先来看看我们可以做些什么。
判断一个节点V是否对节点W感兴趣,就是要判断是否存在一个rank大于r(W)的节点U,δ(V, U)<δ(V, W)。所以,节点V到某个特定的rank的节点(集合)的最短距离是一个非常重要的值。如果我们可以在O(nlog2n)时间内求出所有节点到特定rank的节点(集合)的最短距离,我们就成功地完成了算法的一个重要环节。
用Dijkstva算法反过来求特定rank的节点(集合)到所有点的最短距离——以所有特定rank的节点为起点(rank=1, 2, 3, …或10),求这一点集到所有点的最短距离。由于图中与每个点关联的边最多只有10条,所以图中的边数最多为5n。用Priority Queue(Heap, Winner Tree或Fibonacci Heap等)来实现Dijkstra算法,时间复杂度为O((n+e)log2n)(用Fibonacci Heap实现,更确切的时间复杂度是O(nlog2n+e))。这里,e=5n,因而求一遍最短路径的时间复杂度为O(nlog2n)。由于1≤rank≤10,每个rank都要求一遍最短路径,所以求出每个节点到所有rank的最短路径长度的时间复杂度为O(10*(5+1)nlog2n),即O(nlog2n)。
求出所有点到特定rank的节点(集合)的最短距离,就完成了判断任意节点V对W是否感兴趣的一半工作。另一半是求任意节点V到W的最短距离。前面求节点到rank的最短距离时,利用的是rank范围之小——只有10种,以10个rank集合作起点,用Dijkstra算法求10次最短路径。但是,如果是求任意两点的最短路径,就不可能只求很少次数的最短路径了。一般来说,求任意两点最短路径是Ω(n2)的(这只是一个很松的下界),这样的规模已经远远超出了可承受的范围。但是,要判断V对W是否感兴趣,δ(V, W)又是必须求的,所以n次Dijkstra算法求最短路径肯定是逃不掉的(或者也可以用一次Floyd算法代替,但是时间复杂度一样,可认为等价)。那么,我们又能从哪里来降这个时间复杂度呢?
题目中提到:所有服务器储存的数据量(|B(V)|之和)不会超过30n。这就是说,最多只存在30n对(V, W)满足V对W感兴趣。所以,就本题来说,我们需要处理的点对最少可能只有30n个,求最短距离的下界也就变成Ω(30n)=Ω(n)了(当然,这也只是很松的下界)。虽说下界是Ω(n),其实我们只需要有O(nlog2n)的算法就可以满足要求了。
从前面估算下界的过程中我们也看到,计算在下界中的代价都是感兴趣的点对(一个节点对另一个节点感兴趣),其余部分为不感兴趣的点对。我们如果想降低时间复杂度,就要避免不必要的计算,即避免计算不感兴趣的点对的最短路径。
我们来看当V对W不感兴趣时的情况。根据定义,δ(V, W)>δ(V, r(W)+1)。如果是以W为起点,用Dijkstra算法求最短路径的话。当扩展到V时,发现V对W不感兴趣,即δ(V, W)>δ(V, r(W)+1)。那么,如果再由V扩展求得到U的最短路径,则:
δ(U, W)=δ(V, W)+δ(U, V),
δ(U, r(W)+1)=δ(V, r(W)+1)+δ(U, V),
由于δ(V, W)>δ(V, r(W)+1),
所以δ(V, W)+δ(U, V)>δ(V, r(W)+1)+δ(U, V),即δ(U, W)>δ(U, r(W)+1)
所以,U对W也不感兴趣。因此,如果以W为起点,求其他点到W的最短路径,以判断其他点是否对W感兴趣,当扩展到对W不感兴趣的节点时,就可以不继续扩展下去了(只扩展对W感兴趣的节点)。
我们知道,所有感兴趣的点对不超过30n。因此,以所有点作起点,用Dijkstra算法求最短路径的时间复杂度可由平摊分析得为O(30(n+e)log2n)=O(30(n+5n)log2n)=O(nlog2n)。
由此,我们看到判断一节点是否对另一节点感兴趣,两个关键的步骤都可以在O(nlog2n)时间内完成。当然算法的系数是很大的,不过由于n不大,这个时间复杂度还是完全可以承受的。下面就总结一下前面得到的算法:
(1)分别以rank=1, 2, …, 10的节点(集合)作为起点,求该节点(集合)到所有点的最短距离(其实也就是所有点到该节点(集合)的最短距离);
(2)以每个点作为起点,求该点到所有点的最短距离。当求得某节点的最短距离的同时根据求得的最短距离和该节点到rank大于起点的节点(集合)的最短距离,判断该节点是否对起点感兴趣。如果感兴趣,则找到一对感兴趣的点对,否则,停止扩展该节点,因为该节点不可能扩展出对起点感兴趣的节点。
总结解题的过程,可以发现解决本题的关键有三点:一是稀疏图,正因为图中边比较稀疏所以我们可以用Dijkstra+Priority Queue的方法将求最短路径的时间复杂度降为O(nlog2n);二是rank的范围很小,rank的范围只有10,所以我们只用了10次Dijkstra算法就求得了所有点到特定rank的最短距离;三是感兴趣的点对只有很少,由于感兴趣的点对只有30n,我们通过只计算感兴趣点对的最短路径,将求点与点间最短路径的时间复杂度降到了O(nlog2n)。这三点,只要有一点没有抓住。本题就不可能得到解决。
| 源程序名 age.???(pas, c, cpp) 可执行文件名 age.exe 输入文件名 age.in 输出文件名 age.out |
【问题描述】
由于外国间谍的大量渗入,国家安全正处于高度的危机之中。如果A间谍手中掌握着关于B间谍的犯罪证据,则称A可以揭发B。有些间谍收受贿赂,只要给他们一定数量的美元,他们就愿意交出手中掌握的全部情报。所以,如果我们能够收买一些间谍的话,我们就可能控制间谍网中的每一分子。因为一旦我们逮捕了一个间谍,他手中掌握的情报都将归我们所有,这样就有可能逮捕新的间谍,掌握新的情报。
我们的反间谍机关提供了一份资料,色括所有已知的受贿的间谍,以及他们愿意收受的具体数额。同时我们还知道哪些间谍手中具体掌握了哪些间谍的资料。假设总共有n个间谍(n不超过3000),每个间谍分别用1到3000的整数来标识。
请根据这份资料,判断我们是否有可能控制全部的间谍,如果可以,求出我们所需要支付的最少资金。否则,输出不能被控制的一个间谍。
【输入】
输入文件age.in第一行只有一个整数n。
第二行是整数p。表示愿意被收买的人数,1≤p≤n。
接下来的p行,每行有两个整数,第一个数是一个愿意被收买的间谍的编号,第二个数表示他将会被收买的数额。这个数额不超过20000。
紧跟着一行只有一个整数r,1≤r≤8000。然后r行,每行两个正整数,表示数对(A, B),A间谍掌握B间谍的证据。
【输出】
答案输出到age.out。
如果可以控制所有间谍,第一行输出YES,并在第二行输出所需要支付的贿金最小值。否则输出NO,并在第二行输出不能控制的间谍中,编号最小的间谍编号。
【样例1】
age.in age.out
3 YES
2 110
1 10
2 100
2
1 3
2 3
【样例2】
age.in age.out
4 NO
2 3
1 100
4 200
2
1 2
3 4
【算法分析】
根据题中给出的间谍的相互控制关系,建立有向图。找出有向图中的所有强连通分量,用每个强连通分量中最便宜的点(需支付最少贿金的间谍)来代替这些强连通分量,将强连通分量收缩为单个节点。收缩强连通分量后的图中,入度为0的节点即代表需要贿赂的间谍。
| 源程序名 guards.???(pas, c, cpp) 可执行文件名 guards.exe 输入文件名 guards.in 输出文件名 guards.out |
【问题描述】
从前有一个王国,这个王国的城堡是一个矩形,被分为M×N个方格。一些方格是墙,而另一些是空地。这个王国的国王在城堡里设了一些陷阱,每个陷阱占据一块空地。
一天,国王决定在城堡里布置守卫,他希望安排尽量多的守卫。守卫们都是经过严格训练的,所以一旦他们发现同行或同列中有人的话,他们立即向那人射击。因此,国王希望能够合理地布置守卫,使他们互相之间不能看见,这样他们就不可能互相射击了。守卫们只能被布置在空地上,不能被布置在陷阱或墙上,且一块空地只能布置一个守卫。如果两个守卫在同一行或同一列,并且他们之间没有墙的话,他们就能互相看见。(守卫就像象棋里的车一样)
你的任务是写一个程序,根据给定的城堡,计算最多可布置多少个守卫,并设计出布置的方案。
【输入】
第一行两个整数M和N(1≤M,N≤200),表示城堡的规模。
接下来M行N列的整数,描述的是城堡的地形。第i行j列的数用ai,j表示。
ai,j=0,表示方格[i,j]是一块空地;
ai,j=1,表示方格[i,j]是一个陷阱;
ai,j=2,表示方格[i,j]是墙。
【输出】
第一行一个整数K,表示最多可布置K个守卫。
此后K行,每行两个整数xi和yi,描述一个守卫的位置。
【样例】
guards.in guards.out
3 4 2
2 0 0 0 1 2
2 2 2 1 3 3
0 1 0 2
样例数据如图5-2(黑色方格为墙,白色方格为空地,圆圈为陷阱,G表示守卫)
| ○ | |||
| ○ |
| G | |||
| ○ | |||
| ○ | G |
【算法分析】
本题的关键在构图。
城堡其实就是一个棋盘。我们把棋盘上横向和纵向连续的极长段(不含墙)都分离出来。显然,每一段上最多只能放一个guard,而且guard总是放在一个纵向段和一个横向段的交界处,所以一个guard和一个纵向段和一个横向段有关。
我们把纵向段和横向段都抽象成图中的节点,如果一个纵向段和一个横向段相交的话,就在两点之间连一条边。这样,guard就成为了图中的边。前面得出的性质抽象成图的语言就是,每个点只能和一条边相连,每条边只能连接一个纵向边的点和一个横向边的点。因此,这样的图是二分图,我们所求的正是二分图的匹配。而要布置最多的guards,就是匹配数要最大,即最大匹配。
图中节点数为n(n≤200),求最大匹配的时间复杂度为O(n2.5)。
| 源程序名 kleague.???(pas, c, cpp) 可执行文件名 kleague.exe 输入文件名 kleague.in 输出文件名 kleague.out |
【问题描述】
K-联赛职业足球俱乐部的球迷们都是有组织的训练有素的啦啦队员,就像红魔啦啦队一样(2002年韩日世界杯上韩国队的啦啦队)。这个赛季,经过很多场比赛以后,球迷们希望知道他们支持的球队是否还有机会赢得最后的联赛冠军。换句话说,球队是否可以通过某种特定的比赛结果最终取得最高的积分(获胜场次最多)。(允许出现多支队并列第一的情况。)
现在,给出每个队的胜负场数,wi和di,分别表示teami的胜场和负场(1≤i≤n)。还给出ai,j,表示teami和teamj之间还剩多少场比赛要进行(1≤i,j≤n)。这里,n表示参加联赛的队数,所有的队分别用1,2,…,n来编号。你的任务是找出所有还有可能获得冠军的球队。
所有队参加的比赛数是相同的,并且为了简化问题,你可以认为不存在平局(比赛结果只有胜或负两种)。
【输入】
第一行一个整数n(1≤n≤25),表示联赛中的队数。
第二行2n个数,w1,d1,w2,d2,……,wn,dn,所有的数不超过100。
第三行n2个数,a1,1,a1,2,…,a1,n,a2,1,…,a2,2,a2,n,…,an,1,an,2,…,an,n,所有的数都不超过10。ai,j=aj,i,如果i=j,则ai,j=0。
【输出】
仅一行,输出所有可能获得冠军的球队,按其编号升序输出,中间用空格分隔。
【样例1】
kleague.in kleague.out
3 1 2 3
2 0 1 1 0 2
0 2 2 2 0 2 2 2 0
【样例2】
kleague.in kleague.out
3 1 2
4 0 2 2 0 4
0 1 1 1 0 1 1 1 0
【样例3】
kleague.in kleague.out
4 2 4
0 3 3 1 1 3 3 0
0 0 0 2 0 0 1 0 0 1 0 0 2 0 0 0
【算法分析】
看一个队是否有希望夺冠,首先,这个队此后的比赛自然是赢越多越好,所以先让这个队把以后的比赛都赢下来,算出这个队最高能拿多少分。下面关键就看是否有可能让其他队的积分都低于刚才计算出的最高分。
建立一个网络,所有的球队作为图中的节点,每两个队之间的比赛也作为图中的节点。从网络的源各连一条边到“比赛的节点”,容量为两队间还剩的比赛场数。从“每个队的节点”都连一条边到网络的汇,容量为这个队当前的积分与最高分之差。如果一个“比赛的节点”代表的是A与B之间的比赛,那么从这个节点连两条边分别到“A队的节点”和“B队的节点”,容量为无穷大。
如果这个网络的最大流等于所有还未进行的比赛的场次之和,那么需要我们判断的那个队抗有可能夺得冠军。
本题要我们找出所有可能夺冠的队,那么只需枚举所有的球队,判断它们是否有可能夺冠即可。
| 源程序名 machine.???(pas, c, cpp) 可执行文件名 machine.exe 输入文件名 machine.in 输出文件名 machine.out |
【问题描述】
我们知道机器调度是计算机科学中一个非常经典的问题。调度问题有很多种,具体条件不同,问题就不同。现在我们要处理的是两个机器的调度问题。
有两个机器A和B。机器A有n种工作模式,我们称之为mode_0,mode_l,……,mode_n-1。同样,机器B有m种工作模式,我们称之为mode_0,mode_1,……,mode_m-1。初始时,两台机器的工作模式均为mode_0。现在有k个任务,每个工作都可以在两台机器中任意一台的特定的模式下被加工。例如,job0能在机器A的mode_3或机器B的mode_4下被加工,jobl能在机器A的mode_2或机器B的mode_4下被加工,等等。因此,对于任意的jobi,我们可以用三元组(i,x,y)来表示jobi在机器A的mode_x或机器B的mode_y下被加工。
显然,要完成所有工作,我们需要不时的改变机器的工作模式。但是,改变机器的工作状态就必须重启机器,这是需要代价的。你的任务是,合理的分配任务给适当的机器,使机器的重启次数尽量少。
【输入】
第一行三个整数n,m(n,m<100),k(k<1000)。接下来的k行,每行三个整数i,x,y。
【输出】
只一行一个整数,表示最少的重启次数。
【样例】
machine.in machine.out
5 5 10 3
0 1 1
1 1 2
2 1 3
3 1 4
4 2 1
5 2 2
6 2 3
7 2 4
8 3 3
9 4 3
【问题分析】
本题所求的是工作模式的最少切换次数,实际上也就是求最少需要使用多少个工作模式,因为一个工作模式被切换两次肯定是不合算的,一旦切换到一个工作模式就应该把这个工作模式可以完成的工作都完成。
将两台机器的工作模式分别看成n个和m个节点。jobi分别和机器A和B的mode_x和mode_y相关:jobi要被完成,就必须切换到机器A的mode_x或切换到机器B的mode_y。将jobi看作图中的一条边——连接节点x和节点y的边,那么这条边就要求x和y两个节点中至少要有一个节点被取出来。这正符合覆盖集的性质。
我们构成的图是二分图,要求最少的切换次数,就是要使覆盖集最小。二分图的最小覆盖集问题等价于二分图的最大匹配问题。因此,只需对此二分图求一个最大匹配即是我们要求的答案。时间复杂度
![]()
正在上传…重新上传取消。
| 源程序名 road.???(pas, c, cpp) 可执行文件名 road.exe 输入文件名 road.in 输出文件名 road.out |
【问题描述】
某国有n个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
(1)如果两个或以上城市申请修建同一条公路,则让它们共同修建;
![]()
正在上传…重新上传取消(2)如果三个或以上的城市申请修建的公路成环。如下图,A申请修建公路AB,B申请修建公路BC,C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请;
(3)其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相:连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
【输入】
第一行一个整数n,表示城市的数量。(n≤5000)
以下n行,每行两个整数x和y,表示一个城市的坐标。(-1000000≤x,y≤1000000)
![]()
正在上传…重新上传取消【输出】
一个实数,四舍五入保留两位小数,表示公路总长。(保证有惟一解)
【样例】
road.in road.out 修建的公路如图所示:
4 6.47
0 0
1 2
-1 2
0 4
【问题分析】
三条规则中的第二条是故弄玄虚。如果三个或三个以上的城市申请修建的公路成环,那么这些公路的长度必然都相同,否则不满足“每个城市选择一个与它最近的城市,申请修建通往该城市的公路”。所以,如果成环,其实是任意去掉一条路。
本题要我们求的实际上是最小成成树,也就是说,按规则生成的是图的最小生成树。为什么呢?很显然,按规则生成的应该是树。根据规则:每个城市选择一个与它最近的城市,申请修建通往该城市的公路。那么,对于图中任意的环,环上最长边必被舍弃。这就与求最小生成树的“破环法”完全相符了。
用Prim算法求图中的最小生成树,最小生成树上各边的长度只和即是所求的答案。时间复杂度为O(n2)。
但是,本题还有其特殊性。本题是在Euclid空间求最小生成树,Euclid空间最小生成树有O(nlog2n)的算法,是用Voronoi图+Kruskal算法(或用Prim+heap代替Kruskal)实现的。
| 源程序名 speed.???(pas, c, cpp) 可执行文件名 speed.exe 输入文件名 speed.in 输出文件名 speed.out |
【问题描述】
在这个繁忙的社会中,我们往往不再去选择最短的道路,而是选择最快的路线。开车时每条道路的限速成为最关键的问题。不幸的是,有一些限速的标志丢失了,因此你无法得知应该开多快。一种可以辩解的解决方案是,按照原来的速度行驶。你的任务是计算两地间的最快路线。
你将获得一份现代化城市的道路交通信息。为了使问题简化,地图只包括路口和道路。每条道路是有向的,只连接了两条道路,并且最多只有一块限速标志,位于路的起点。两地A和B,最多只有一条道路从A连接到B。你可以假设加速能够在瞬间完成并且不会有交通堵塞等情况影响你。当然,你的车速不能超过当前的速度限制。
【输入】
输入文件SPEED.IN的第一行是3个整数N,M和D(2<=N<=150),表示道路的数目,用0..N-1标记。M是道路的总数,D表示你的目的地。接下来的M行,每行描述一条道路,每行有4个整数A(0≤A<N),B(0≤B<N),V(0≤V≤500)and L(1≤L≤500),这条路是从A到B的,速度限制是V,长度为L。如果V是0,表示这条路的限速未知。如果V不为0,则经过该路的时间T=L/V。否则T=L/Vold,Vold是你到达该路口前的速度。开始时你位于0点,并且速度为70。
【输出】
输出文件SPEED.OUT仅一行整数,表示从0到D经过的城市。
输出的顺序必须按照你经过这些城市的顺序,以0开始,以D结束。仅有一条最快路线。
【样例】
speed.in speed.out
6 15 1 0 5 2 3 1
0 1 25 68
0 2 30 50
0 5 0 101
1 2 70 77
1 3 35 42
2 0 0 22
2 1 40 86
2 3 0 23
2 4 45 40
3 1 64 14
3 5 0 23
4 1 95 8
5 1 0 84
5 2 90 64
5 3 36 40
【问题分析】
首先,利用预处理计算任意两个节点之间只经过无限速标志的路的最短距离。这可以用F1ovd算法得到,时间复杂度为O(n3)。
计算城市1到城市D之间最快路径时,只需对Dijkstra稍作修改即可:在Dijkstra算法中,用一个已计算出最短路径的节点去刷新其他节点当前最短路径长度时,除了要枚举有限速标志的路以外,还要在此路的基础上,枚举通过此路后要经过无限速标志的路到达的节点。时间复杂度为O(n2+mn),即O(mn)。
第六章 树
| 源程序名 tree.???(pas, c, cpp) 可执行文件名 tree.exe 输入文件名 tree.in 输出文件名 tree.out |
![]()
正在上传…重新上传取消【问题描述】
一个边长为n的正三角形可以被划分成若干个小的边长为1的正三角形,称为单位三
角形。如右图,边长为3的正三角形被分成三层共9个小的正三角形,我们把它们从顶到
底,从左到右以1~9编号,见右图。同理,边长为n的正三角形可以划分成n2个单位三
角形。
![]()
正在上传…重新上传取消 四个这样的边长为n的正三角形可以组成一个三棱锥。我们将正三棱锥的三个侧面依
顺时针次序(从顶向底视角)编号为A, B, C,底面编号为D。侧面的A, B, C号三角形以
三棱锥的顶点为顶,底面的D号三角形以它与A,B三角形的交点为顶。左图为三棱锥展
开后的平面图,每个面上标有圆点的是该面的顶,该图中侧面A, B, C分别向纸内方向折
叠即可还原成三棱锥。我们把这A,B、C、D四个面各自划分成n2个单位三角形。
对于任意两个单位三角形,如有一条边相邻,则称它们为相邻的单位三角形。显然,每个单位三角形有三个相邻的单位三角形。现在,把1—4n2分别随机填入四个面总共4n2个单位三角形中。
现在要求你编程求由单位三角形组成的最大排序二叉树。所谓最大排序二叉树,是指在所有由单位三角形组成的排序二叉树中节点最多的一棵树.对于任一单位三角形,可选它三个相邻的单位三角形中任意一个作为父节点,其余两个分别作为左孩子和右孩子。当然,做根节点的单位三角形不需要父节点,而左孩子和右孩于对于二叉树中的任意节点来说并不是都必须的。
【输入】
输入文件为tree.in。其中第一行是一个整数n(1<=n<=18),随后的4n2个数,依次为三棱锥四个面上所填的数字。
【输出】
输出文件为tree.out。其中仅包含一个整数,表示最大的排序二又树所含的节点数目。
【样例】
输入文件对应下图:
![]()
正在上传…重新上传取消
A B C D
tree.in tree.out
3 22 13 9 17
19 25 15 1
33 20 26 28
32 21 18 7
31 12 17 2
29 24 8 6
3 23 16 36
5 34 27
4 35 11
30 14 10
输出样例文件对应的最大排序二叉树如下图所示:
![]()
正在上传…重新上传取消
【知识准备】
记忆化搜索的基本概念和实现方法。
【算法分析】
在讨论问题的解法之前,我们先来看看二叉排序树的性质。
二叉排序树是一棵满足下列性质的二又树:
性质1 它或是一棵空树,或是一棵二叉树,满足左子树的所有结点的值都小于根结点的值,右子树的所有结点的值都大于根结点的值;
性质2 它若有子树,则它的子树也是二叉排序树。
根据性质1,我们可以知道,二叉排序树的左右子树是互不交叉的。也就是说,如果确定了根结点,那么我们就可以将余下的结点分成两个集合,其中一个集合的元素可能在左子树上,另一集合的元素可能在右子树上,而没有一个结点同时可以属于两个集合。这一条性质,满足了无后效性的要求,正因为二叉排序树的左右子树是互不交叉的,所以如果确定根结点后,求得的左子树,对求右子树是毫无影响的。因此,如果要使排序树尽可能大,就必须满足左右子树各自都是最大的,即局部最优满足全局最优。
根据性质2,二叉排序树的左右子树也是二叉排序树。而前面已经分析得到,左右子树也必须是极大的。所以,求子树的过程也是一个求极大二叉排序树的过程,是原问题的一个子问题。那么,求二叉排序树的过程就可以分成若干个阶段来执行,每个阶段就是求一棵极大的二叉排序子树。
由此,我们看到,本题中,二叉排序树满足阶段性(性质2)和无后效性(性质1),可以用动态规划解决。
下面来看具体解决问题的方法。
不用说,首先必须对给出的正三棱锥建图,建成一张普通的无向图。
根据正三棱锥中结点的性质,每个结点均与三个结点相连。而根据二叉排序树的性质,当一个结点成为另一个结点的子结点后,它属于左子树还是右子树也就确定下来了。所以,可以对每个结点进行状态分离,分离出三种状态——该结点作为与它相连的三个结点的子结点时,所得的子树的状态。但是,一个子结点可以根据它的父结点知道的仅仅是该子树的一个界(左子树为上界,右子树为下界),还有一个界不确定,所以还需对分离出来的状态再进行状态分离,每个状态代表以一个值为界(上界或下界)时的子树状态。
整个分离过程如下图所示:
![]()
正在上传…重新上传取消
确定了状态后,我们要做的事就是推出状态转移方程。
前面已经提到,一个极大的二叉排序树,它的左右子树也必须是极大的。因此,如果我们确定以结点n为根结点,设所有可以作为它左子结点的集合为N1,所有可以作为它右子结点的集合为N2,则以n为根结点、结点大小在区间[l, r]上的最大二叉排序树的结点个数为:
![]()
正在上传…重新上传取消
我们所要求的最大的二叉排序树的结点个数为:
![]()
正在上传…重新上传取消,其中n为结点的总个数
从转移方程来看,我们定义的状态是三维的。那么,时间复杂度理应为O(n3)。其实并非如此。每个结点的状态虽然包含下界和上界,但是不论是左子结点还是右子结点,它的一个界取决于它的父结点,也就是一个界可用它所属的父结点来表示,真正需要分离的只有一维状态,要计算的也只有一维。因此,本题时间复杂度是O(n2)(更准确的说应该是O(3n2))。
此外,由于本题呈现一个无向图结构,如果用递推形式来实现动态规划,不免带来很大的麻烦。因为无向图的阶段性是很不明显的,尽管我们从树结构中分出了阶段。不过,实现动态规划的方式不仅仅是递推,还可以使用搜索形式——记忆化搜索。用记忆化搜索来实现本题的动态规划可以大大降低编程复杂度。
6.2 树的重量
| 源程序名 weight.???(pas, c, cpp) 可执行文件名 weight.exe 输入文件名 weight.in 输出文件名 weight.out |
【问题描述】
树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树,其叶节点表示一个物种,两个叶节点之间的距离表示两个物种的差异。现在,一个重要的问题是,根据物种之间的距离,重构相应的“进化树”。
令N={1..n},用一个N上的矩阵M来定义树T。其中,矩阵M满足:对于任意的i,j,k,有M[i,j]+M[j,k]<=M[i,k]。树T满足:
1.叶节点属于集合N;
2.边权均为非负整数;
3.dT(i,j)=M[i,j],其中dT(i,j)表示树上i到j的最短路径长度。
如下图,矩阵M描述了一棵树。
![]()
正在上传…重新上传取消
树的重量是指树上所有边权之和。对于任意给出的合法矩阵M,它所能表示树的重量是惟一确定的,不可能找到两棵不同重量的树,它们都符合矩阵M。你的任务就是,根据给出的矩阵M,计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树,这棵树的总重量为15。
![]()
正在上传…重新上传取消
【输入】
输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-l行,给出的是矩阵M的一个上三角(不包含对角线),矩阵中所有元素是不超过100的非负整数。输入数据保证合法。
输入数据以n=0结尾。
【输出】
对于每组输入,输出一行,一个整数,表示树的重量。
【样例】
weight.in weight.out
5 15
5 9 12 8 71
8 11 7
5 1
4
4
15 36 60
31 55
36
0
【知识准备】
树的基本特征。
【算法分析】
本题是一道涉及树性质的算法题,所以我们应该以树的性质为突破口,来讨论本题的算法。
首先来看一下简单的实例,就以题目中给出的例子来说明。下图所示的树,有5个叶子节点,两个内点,6条边。我们已知的信息是任意两个叶子节点之间的距离,所以我们讨论的必然是叶子节点之间的关系,不可能涉及内点。
![]()
正在上传…重新上传取消
从图中我们可以看出,有些叶子结点是连在同一个内点上的,如①和②;也有些连在不同的内点上,如①和④。我们来看连在同一内点上的叶子节点有什么特殊的性质。就以①和②为例,①到③、④、⑤的距离分别为9、12、8,②到③、④、⑤的距离分别为8、11、7,正好都相差l。这个“1”差在哪里呢?①连到内点的边长为3,②连到内点的边长为2,两者相差为1。所以,相差的“1”正好就是两节点连到内点上的边长的差。再看①到②的距离,由于两叶子节点都是连在同一个内点上的,所以他们之间的距离,就是两者到内点的边长和。知道的边长和以及边长差,求出两边长就不难做到了。(注意:两叶子节点连到内点的边长是未知的)
再看一下不连在同一内点上的节点,①和④。①到②、③、⑤的距离分别为5、9、8,④到②、③、⑤的距离分别为11、5、4,没有一个统一的“差”。
其实,前面的结论都是非常直观而显然的,只不过关键是如何去利用。我们先来总结一下前面的结论:
(1)如果两叶子节点连在同一个内点上,则它们到其他叶子节点的距离有一个统一的“差”;
(2)如果两叶子节点连在不同的内点上,则它们到其他叶子节点的距离没有一个统一的“差”;
○
/
○────●────●
a \
○
值得注意的是,图6-3中的a点不能算内点。我们所指的内点是至少连接两个叶子节点的点,像a这样的点完全可以去掉,不会影响树的权值和,如下图。
○
/
○─────────●
\
○
(3)如果两叶子节点连在同一个内点上,则它们之间的距离等于它们各自到内点的边长的和。
根据(1)和(2)两条性质,很容易得到判断连接相同内点的两个叶子节点的方法,即必须满足它们到其他所有叶子节点有统一的距离差(充分且必要)。
找到两个连接相同内点的叶子节点并计算出它们各自到内点的边长(不妨设为l1和l2)以后,我们可以作这样的操作:删去一个节点,令另一个节点到内点的边长为l1+l2。这样得到的新树,权值和与原树相同,但叶子节点少了一个,如下图。
![]()
正在上传…重新上传取消
反复利用上述操作,最后会得到一棵只有两个叶子节点的树,这两个节点之间的边长就是原树的权值和。
算法需要反复执行n-2次删除节点的操作。每次操作中,需要枚举两个叶子节点,并且还要有一个一维的判断,时间复杂度是O(n3)的。所以,整个算法的时间复杂度是O(n4)的。对于一个规模仅有30的题目来说,O(n4)的算法足以解决问题了。当然,算法本身应该还是有改进的余地的,不过这里就不加以讨论了。
6.3 信号放大器
| 源程序名 booster.???(pas, c, cpp) 可执行文件名 booster.exe 输入文件名 booster.in 输出文件名 booster.out |
【问题描述】
树型网络是最节省材料的网络。所谓树型网络,是指一个无环的连通网络,网络中任意两个结点间有且仅有一条通信道路。
网络中有一个结点是服务器,负责将信号直接或间接地发送到各终端机。如图6-4,server结点发出一个信号给结点a和c,a再转发给b。如此,整个网络都收到这个信号了。
server a b
●────○────○
│
│
○
但是,实际操作中,信号从一个结点发到另一个结点,会出现信号强度的衰减。衰减量一般由线路长度决定。 server 3 a 2 b
●────○────○
│
│1
○
如上图,边上所标的数字为边的衰减量。假设从server出发一个强度为4个单位的信号,发到结点a后强度衰减为4-3=1个单位。结点a再将其转发给结点b。由于信号强度为1,衰减量为2,因此信号无法发送到b。
一个解决这一问题的方法是,安装信号放大器。信号放大器的作用是将强度大于零的信号还原成初始强度(从服务器出发时的强度)。
上图中,若在结点a处安装一个信号放大器,则强度为4的信号发到a处,即被放大至4。这样,信号就可以被发送的网络中的任意一个节点了。为了简化问题,我们假定每个结点只处理一次信号,当它第二次收到某个信号时,就忽略此信号。
你的任务是根据给出的树型网络,计算出最少需要安装的信号放大器数量。
【输入】
第一行一个整数n,表示网络中结点的数量。(n<=100000)
第2~n+1行,每行描述一个节点的连接关系。其中第i+1行,描述的是结点i的连接关系:首先一个整数k,表示与结点i相连的结点的数量。此后2k个数,每两个描述一个与结点i相连的结点,分别表示结点的编号(编号在1~n之间)和该结点与结点i之间的边的信号衰减量。结点1表示服务器。
最后一行,一个整数,表示从服务器上出发信号的强度。
【输出】
一个整数,表示要使信号能够传遍整个网络,需要安装的最少的信号放大器数量。
如果不论如何安装信号放大器,都无法使信号传遍整个网络,则输出“No solution.”
【样例】
booster.in booster.out
4 1
2 2 3 3 1
2 1 3 4 2
1 1 1
1 2 2
4
【问题分析】
用贪心算法求解。从叶结点往根结点回推,当信号强度不够继续传送时,即增加一个信号放大器。算法的时间复杂度为O(n)。
| 源程序名 gallery.???(pas, c, cpp) 可执行文件名 gallery.exe 输入文件名 gallery.in 输出文件名 gallery.out |
【问题描述】
经过数月的精心准备,Peer Brelstet,一个出了名的盗画者,准备开始他的下一个行动。艺术馆的结构,每条走廊要么分叉为两条走廊,要么通向一个展览室。Peer知道每个展室里藏画的数量,并且他精确测量了通过每条走廊的时间。由于经验老到,他拿下一幅画需要5秒的时间。你的任务是编一个程序,计算在警察赶来之前,他最多能偷到多少幅画。
![]()
正在上传…重新上传取消
【输入】
第1行是警察赶到的时间,以s为单位。第2行描述了艺术馆的结构,是一串非负整数,成对地出现:每一对的第一个数是走过一条走廊的时间,第2个数是它末端的藏画数量;如果第2个数是0,那么说明这条走廊分叉为两条另外的走廊。数据按照深度优先的次序给出,请看样例。
一个展室最多有20幅画。通过每个走廊的时间不超过20s。艺术馆最多有100个展室。警察赶到的时间在10min以内。
【输出】
输出偷到的画的数量。
【样例】
gallery.in(如图6-6) gallery.out
60 2
7 0 8 0 3 1 14 2 10 0 12 4 6 2
【问题分析】
用树型动态规划求解。首先,题目保证数是二叉树。定义状态f(n, t)表示在结点n所在子树上花t时间所能取到的最大分值,则状态转移方程为
f(n, t)=max{f(left, t0)+f(right, t-t0)}
其中left和right为n的左右子结点,t0的取值范围为[0, t]。
算法的时间复杂度为O(n3)。
| 源程序名 party.???(pas, c, cpp) 可执行文件名 party.exe 输入文件名 party.in 输出文件名 party.out |
【问题描述】
你要组织一个由你公司的人参加的聚会。你希望聚会非常愉快,尽可能多地找些有趣的热闹。但是劝你不要同时邀请某个人和他的上司,因为这可能带来争吵。给定N个人(姓名,他幽默的系数,以及他上司的名字),编程找到能使幽默系数和最大的若干个人。
【输入】
第一行一个整数N(N<100)。接下来有N行,每一行描述一个人的信息,信息之间用空格隔开。姓名是长度不超过20的字符串,幽默系数是在0到100之间的整数。
【输出】
所邀请的人最大的幽默系数和。
【样例】
party.in party.out
5 8
BART 1 HOMER
HOMER 2 MONTGOMERY
MONTGOMERY 1 NOBODY
LISA 3 HOMER
SMITHERS 4 MONTGOMERY
【问题分析】
用动态规划求解。首先,很显然公司的人员关系构成了一棵树。设f[a]为a参加会议的情况下,以他为根的子树取得的最大幽默值;g[a]为a不参加会议的情况下,以他为根的子树取得的最大幽默值。那么,状态转移方程就是:
f[a]=g[b1]+g[b2]+…+g[bk]+1
g[a]=max(f[b1], g[b1])+max(f[b2], g[b2])+…+max(f[bk], g[bk])
其中b1, b2, …, bk为a的子结点。
最后的答案就是max(f[root], g[root]),root是树根。
| 源程序名 roads.???(pas, c, cpp) 可执行文件名 roads.exe 输入文件名 roads.in 输出文件名 roads.out |
【问题描述】
一场可怕的地震后,人们用N个牲口棚(1≤N≤150,编号1..N)重建了农夫John的牧场。由于人们没有时间建设多余的道路,所以现在从一个牲口棚到另一个牲口棚的道路是惟一的。因此,牧场运输系统可以被构建成一棵树。John想要知道另一次地震会造成多严重的破坏。有些道路一旦被毁坏,就会使一棵含有P(1≤P≤N)个牲口棚的子树和剩余的牲口棚分离,John想知道这些道路的最小数目。
【输入】
第1行:2个整数,N和P
第2..N行:每行2个整数I和J,表示节点I是节点J的父节点。
【输出】
单独一行,包含一旦被破坏将分离出恰含P个节点的子树的道路的最小数目。
【样例】
roads.in roads.out
11 6 2
1 2
1 3
1 4
1 5
2 6
2 7
2 8
4 9
4 10
4 11
【样例解释】
如果道路1-4和1-5被破坏,含有节点(1,2,3,6,7,8)的子树将被分离出来
【问题分析】
用树型动态规划求解。定义f(n, m)为在n为根的子树中取m个节点的最小代价,则状态转移方程为:
f(n, m)=min{f(n0, m0)+f(n1, m1)+f(n2, m2)+…+f(nk, mk)}
其中,n0, n1, n2, …, nk为n的k个儿子,m0+m1+m2+…+mk=m,并且定义f(ni, 0)=1。
最后的结果为:
min{f(root, p), min{f(n, p) | n≠root}}
| 源程序名 tele.???(pas, c, cpp) 可执行文件名 tele.exe 输入文件名 tele.in 输出文件名 tele.out |
【问题描述】
某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构,这棵树的根结点位于足球比赛的现场,树叶为各个用户终端,其他中转站为该树的内部节点。
从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的,一场转播的总费用等于传输信号的费用总和。
现在每个用户都准备了一笔费用想观看这场精彩的足球比赛,有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。
写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。
【输入】
输入文件的第一行包含两个用空格隔开的整数N和M,其中2≤N≤3000,1≤M≤N-1,N为整个有线电视网的结点总数,M为用户终端的数量。
第一个转播站即树的根结点编号为1,其他的转播站编号为2到N-M,用户终端编号为N-M+1到N。
接下来的N-M行每行表示—个转播站的数据,第i+1行表示第i个转播站的数据,其格式如下:
K A1 C1 A2 C2 … Ak Ck
K表示该转播站下接K个结点(转播站或用户),每个结点对应一对整数A与C,A表示结点编号,C表示从当前转播站传输信号到结点A的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。
【输出】
输出文件仅一行,包含一个整数,表示上述问题所要求的最大用户数。
![]()
正在上传…重新上传取消【样例】
tele.in tele.out
5 3 2
2 2 2 5 3
2 3 2 4 3
3 4 2
【样例解释】
如右图所示,共有五个结点。结点①为根结点,即现场直播站,②为一
个中转站,③④⑤为用户端,共M个,编号从N-M+1到N,他们为观看比
赛分别准备的钱数为3、4、2,从结点①可以传送信号到结点②,费用为2,
也可以传送信号到结点⑤,费用为3(第二行数据所示),从结点②可以传输信号到结点③,费用为2。也可传输信号到结点④,费用为3(第三行数据所示),如果要让所有用户(③④⑤)都能看上比赛,则信号传输的总费用为:
2+3+2+3=10,大于用户愿意支付的总费用3+4+2=9,有线电视网就亏本了,而只让③④两个用户看比赛就不亏本了。
【问题分析】
用动态规划求解。状态这样定义,设F[A, M]为A结点下支持M个用户所能得到的最大赢利。转移方程为:
F[A, M]=Max{F[B1, M1]+F[B2, M2]+…+F[Bk, Mk] | Bi是A的子结点,M1+M2+…+Mk=M}
可以考虑将多叉数转换成二叉树来做,也可以考虑动态地分配内存。这样,空间复杂度约为O(n),时间复杂度为O(n2)。
第七章 搜索
7.1 最多因子数
| 源程序名 divisors.???(pas, c, cpp) 可执行文件名 divisors.exe 输入文件名 divisors.in 输出文件名 divisors.out |
【问题描述】
数学家们喜欢各种类型的有奇怪特性的数。例如,他们认为945是一个有趣的数,因为它是第一个所有约数之和大于本身的奇数。
为了帮助他们寻找有趣的数,你将写一个程序扫描一定范围内的数,并确定在此范围内约数个数最多的那个数。不幸的是,这个数和给定的范围的都比较大,用简单的方法寻找可能需要较多的运行时间。所以请确定你的算法能在几秒内完成最大范围内的扫描。
【输入】
只有一行,给出扫描的范围,由下界L和上界U确定。满足2≤L≤U≤1000000000。
【输出】
对于给定的范围,输出该范围内约数个数D最多的数P。若有多个,则输出最小的那个。请输出“Between L and U,P has a maximum of D divisors.”,其中L,U,P和D的含义同前面所述。
【样例】
divisors.in divisors.out
1000 2000 Between 1000 and 2000, 1680 has a maximum of 40 divisors.
【知识准备】
深度优先搜索的基本实现方法及剪枝的基本概念。
【算法分析】
本题的要求是,求出一个给定区间内的含因子数最多的整数。
首先,有必要明确一下如何求一个数的因子数。若一个数N满足N=P1N1·P2N2·P3N3·…·PmNm,其中P1, P2, …, Pm是N的m个质因子。则N的约数个数为(N1+1)·(N2+1)·(N3+1)·…·(Nm+1)。这一公式可以通过乘法原理来证明。
有了求因子数的公式后,最容易想到的算法就是,枚举区间内的每个整数,统计它们的约数个数。这个算法很容易实现,但是时间复杂度却相当高。因为区间中整数的范围是1~1000000000,整个枚举一遍并计算因子数的代价约为109×(109)0.5=1013.5。这个规模是无法忍受的。所以,我们需要尽量优化时间。
分析一下枚举的过程就会发现,如果我们分别枚举两个数n和p·n(p为一相对较大的质数),那么我们将重复计算两次n的因子数。其实,如果枚举顺序得当的话,完全可以在n的基础上去计算p·n,而如果能在n的基础上计算p·n,就相当于计算p·n的因子数只用了O(1)的时间。这是一个比较形象的例子,类似的(可能相对更复杂一些)重复计算在枚举过程中应该是普遍存在的。这就是枚举效率低的根本所在。为了解决这一重复,我们可以选取另一种搜索顺序——枚举质因子。这样的搜索顺序可以避免前面所说了类似n和p·n的重复计算。
定义number为当前搜索到的数。初始时,令number=1,然后从最小的质数2开始枚举,枚举因子中包含0个2、1个2、2个2、…、k个2的情况……直至number·2k大于区间的上限(max)。对于每个“2k的情况”,令number:=number*2k,在这个基础上,再枚举因子3的情况。然后在3的基础上枚举因子5的情况,然后是7的情况……整个过程是一个深度搜索的过程,搜索的过程中,利用前面提到的求因子数的公式可以算出当前的number的因子数供下一层枚举继承。当number大于等于区间下限(min)时,我们就找到了一个区间内的数(枚举的过程已保证number不超过上界)。所有枚举得到的区间内的数中,因子数的最大值就是我们要求的目标。
这样的枚举完全去除了重复计算,但是这还是不够的,因为光1~1000000000内的数每枚举一遍就有109个单位的操作。所以,我们还需要找到一些剪枝的方法,进一步优化时间。
我们看到,如果当前搜索状态为(from, number, total),其中,from是指当前枚举到的质因子(按从小到大枚举),total是指number中包含的因子数。那么剩下的因子数最多为q=logfrommax/number,这些因子组成的因子个数最大为2q。因此,当前所能取到的(理想情况)最大约数个数就是total·2q。如果这个数仍然无法超过当前最优解,则这一分支不可能产生最优解,可以剪去。
此外,如果[(min-1)/number]=[max/number],则表示以当前状态搜索下去,结果肯定不在区间内了,就无法产生合法解,也可剪去。不过,这一剪枝作用不是很大,因为即使不剪,再搜索一层也就退出了。
以上两个剪枝,前一个是最优化剪枝,后一个是合法性剪枝。相比较而言,前一个剪枝的作用要大得多。
下面我们用平摊分析的方法来讨论一下搜索的复杂度。由于枚举的过程中没有重复计算,每枚举一个质因子,都可以得到一个不同的number(number≤max),所以可以将每一个单位的枚举质因子的代价与一个不超过max的number对应,并且还可在两者之间建立双射。不同的number最多只有max个,所以枚举的总代价不超过O(max),max≤109。
加上了剪枝以后,计算总代价就远远小于O(max)了。从运行效果来看,即便是最大数据,也可以很快出解。
从本题的解决过程中可以看到,最关键的有两步:
(1)采用合理的搜索顺序,避免重复计算;
(2)利用最优化剪枝和合法性剪枝,剪去一些不可能产生最优解或合法解的分支。
这两种优化的方法在搜索中的地位是极其重要的,当然可能在本题中的重要性体现得格外突出。
7.2 黑白棋游戏
| 源程序名 game.???(pas, c, cpp) 可执行文件名 game.exe 输入文件名 game.in 输出文件名 game.out |
【问题描述】
黑白棋游戏的棋盘由4×4方格阵列构成。棋盘的每一方格中放有1枚棋子,共有8枚白棋子和8枚黑棋子。这16枚棋子的每一种放置方案都构成一个游戏状态。在棋盘上拥有1条公共边的2个方格称为相邻方格。一个方格最多可有4个相邻方格。在玩黑白棋游戏时,每一步可将任何2个相邻方格中棋子互换位置。对于给定的初始游戏状态和目标游戏状态,编程计算从初始游戏状态变化到目标游戏状态的最短着棋序列。
【输入】
输入文件共有8行。前四行是初始游戏状态,后四行是目标游戏状态。每行4个数分别表示该行放置的棋子颜色。“0”表示白棋;“1”表示黑棋。
【输出】
输出文件的第一行是着棋步数n。接下来n行,每行4个数分别表示该步交换棋子的两个相邻方格的位置。例如,abcd表示将棋盘上(a,b)处的棋子与(c,d)处的棋子换位。
【样例】
game.in game.out
1111 4
0000 1222
1110 1424
0010 3242
1010 4344
0101
1010
0101
【知识准备】
(1)宽度优先搜索的基本概念;
(2)位操作相关知识。
【算法分析】
本题是一道典型的宽度优先搜索题。宽度优先搜索的方法本身应该是很显然的:根据题目的描述,对于任意一个棋盘状态,可以通过交换相邻两个格子中的棋子得到新的状态(一次最多得到24个新状态)。所以,我们可以从题目给出的起始状态开始不停的扩展,直至扩展出目标状态。最后,只需输出扩展的路径即可。
上述算法已经可以完全解决本题了。但是,我们现在要继续往细节里讨论本题,讨论本题的实现。
宽度优先搜索的核心是状态的扩展,状态的扩展是通过状态转换实现的。普通的状态转换的方法就是按照题目的定义模拟实现。这里,我们要讨论的是高效简洁的状态转换的方法。
首先是状态的表示。题目中的棋盘是由16个格子组成的(4×4),如下图。
| a1 | a2 | a3 | a4 |
| a5 | a6 | a7 | a8 |
| a9 | a10 | a11 | a12 |
| a13 | a14 | a15 | a16 |
这16个格子,每个格子里非0即1,所以可以将棋盘写成一个长度为16的01串。
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 | a16 |
这个0l串可以用一个16bit的整数来表示。也就是说,我们可以用一个0~65535的整数来表示一个状态。
下面最关键的就是状态的转换了。根据题目的定义,每次操作可以交换棋盘上相邻两个格子中的棋子。显然,如果相邻两个格子中的棋子相同,交换是没有意义的,所以我们只需要考虑相邻格子中棋子颜色不同的情况。相邻有两种情况,左右相邻和上下相邻。如图,a1和a2为左右相邻,而a8和a12为上下相邻。我们讨论状态转换的时候,将对这两种“相邻”分别处理。
| a1 | a2 | a3 | a4 |
| a5 | a6 | a7 | a8 |
| a9 | a10 | a11 | a12 |
| a13 | a14 | a15 | a16 |
图7-2
首先来看左右相邻的情况,以a15和a16为例。它们交换以后,得到的棋盘状态为:
| a1 | a2 | a3 | a4 |
| a5 | a6 | a7 | a8 |
| a9 | a10 | a11 | a12 |
| a13 | a14 | a16 | a15 |
图7-3
但是,从另一个角度来考虑问题,a15=??a16,所以经过转换后,就相当于将a15和a16取反。从位操作的角度来看,设原状态为s,那么a15和a16交换后得到的新状态s15为:
s15=s xor 3
同样的,还可以推出a14和a15交换后得到的新状态s14为:
s14=s xor 6=s xor (3*21)
当然,还有以下很多状态公式:
s13=s xor 12=s xor(3*22)
s11=s xor 48=s xor(3*24)
s10=s xor 96=s xor(3*25)
这里有两个需要注意之点:
(1)交换的两个棋子的颜色必须不同,否则公式不成立;
(2)根据状态转换的定义s4、s8、s12、s16对应的公式不成立,因为它们右边没有相邻的棋子。
最后,我们总结一下左右相邻情况下的状态转换公式(棋子颜色必须不同)
sk=s xor(3*215-k),其中k≠4, 8, 12, 16
与“左右相邻”对应的是“上下相邻”。“上下相邻”情况的分析与“左右相邻”类似,这里就不详细展开了,只列出转换的公式(同样,棋子颜色也必须不同)
sk=s xor(17*212-k),其中k≤12
有了上面两个状态转换的公式,我们只需将起始状态和目标状态转换成16bit的整数,利用公式从起始状态扩展至目标状态即可。整个过程的时间复杂度是O(24*216)。
从另一个角度考虑问题。本题给出了起始状态和目标状态,那么我们完全可以从这两个状态开始,分别扩展——也就是用双向宽度优先搜索的方法来解决本题。一般来说,双向搜索扩展出的状态总数要比单向少很多,时间和空间复杂度都会有所降低。
7.3 纵横填字游戏
| 源程序名 puzzle.???(pas, c, cpp) 可执行文件名 puzzle.exe 输入文件名 puzzle.in 输出文件名 puzzle.out |
【问题描述】
这个题目要求你编写一个程序来解决一个纵横填字游戏。
这个游戏比我们在报纸上见到的通常的填字游戏要简单。游戏仅给出单词的起始位置,方面(横向或纵向)以及单词的长度。只要单词的长度正好,游戏中能填入任何一个来自词典的单词。
在游戏中单词相交处的字母必须相同,当然,任何单词只准使用一次。
思考一下以下这个游戏。
例如,假定从上到下有5行,用0到4来表示,从左到右有5列,用0到4来表示。我们用(X, Y)来表示填字游戏中第X列和第Y行的字母。
在这个游戏中,我们需填入5个单词:在(0, 0)的右边填入一个4个字母的单词,在(0, 0)的下方填入一个4个字母的单词,在(2, 0)的下方填入一个4个字母的单词,在(0, 2)的右边填入一个3个字母的单词,最后在(2, 3)的右边填入一个3个字母的单词。字典上所有的单词都能使用但最多只能使用一次。例如,以下是一个可能的解决方案。
(0, 0)右边,LATE
(0, 0)下面,LIED
(2, 0)下面,TELL
(2, 3)右边,LOW
【输入】
输入文件的第一行是作为字典使用的—个文本文件名,你可以假定这个文件存在,是可读的并且包含最多不超过100000个单词,并且按词典顺序存储,每行一个单词。字典中所有的单词所含的字母可以是大写或小写(在这个问题中字母的大小写是无关紧要的)。你可以假设字典中所有单词的长度不超过20个字符。输入文件的下一行包含一个整数n(n≤15),表示要填的单词的数量。接下来的n行中每行给出关于一个单词的提示,在每个提示中分别给出单词的首字母在填字游戏中的列和行的位置,后面根据单词的方向是横向还是纵向,相应跟字符A或字符D,最后一个数表示该单词的长度,以上数据之间均用空格隔开。
你能作以下的进一步的假设。
(1)填字游戏的尺寸不超过10×10。
(2)游戏盘中放得下所有的单词。
(3)用给定的词典是能够破解出该游戏的。
【输出】
输出文件应该包含n行,输出游戏中可填入的所有单词。单词应该每行出现一个,并且按输入文件中提示的顺序输出。每个单词中所有的字母必须是大写的。所有的单词必须来自给定的词典文件(忽略大小写)。任何单词只能使用一次。对于给定输入文件可能有大量的正确解决方案,你只须输出其中的任意一个解决方案。
【样例】
puzzle.in puzzle.out
words.txt LATE
5 LIED
0 0 A 4 TELL
0 0 D 4 EEL
2 0 D 4 LOW
0 2 A 3
2 3 A 3
【知识准备】
(1)深度优先搜索的基本实现方法;
(2)Hash表的基本理论及其实现方法(主要是“吊桶处理冲突法”)。
【算法分析】
本题是一个规模巨大的搜索问题,其规模主要体现在词典(单词表)中的单词数(最多可达到100000),这意味着每在一个空位中填一个单词就可能有100000种选择。
搜索题一般来说都会有很强的剪枝性,但是本题没有,除了一些合法性的剪枝外,基本上找不到任何可行的剪枝,哪怕是效果很弱的剪枝也没有。
先来看看最简单而且能够非常自然想到的搜索方法:一个一个空位枚举,对于题目给出的每个空位在单词表中枚举一个暂时符合要求的单词填进去。这个算法最坏情况的时间复杂度是O(100000n)的(n≤20)。当然,10000020的阶一般是达不到的,但是要达到1000002应该不是很难办到的,而1000002已经足以让程序超时了。
让我们分析一下上面算法的瓶颈。
对于O(100000n)的算法来说,降一点指数其实效果不是非常明显的,因为起码要把n降到1.x才能不超时,而且降指数也不是那么容易办到的。然而,如果能把100000这个底数降低到很小,比方说一个小常数,效果应该就很好了。由于n不大,只有20,如果底数很小的话(设为c),算法的时间复杂度就是O(cn),再加上一些可行性的剪枝,程序的效率应该是很高的。
现在的问题就是,如何来降这个100000的底数了。前面提到的最简单的搜索方法,每枚举一个单词都要扫描一遍单词表,这是极大的浪费,因为单词表中绝大多数的单词都是非法的(根据一般英语词典的情况来说)。实际上,我们扫描一遍单词表的目的是找出所有当前合法的单词,而实现这一目的并非只能用扫描一遍单词表这种方法。
我们知道有一个概率常数级的查找方法——Hash法。
当然,Hash一般是用来查找单一元素的,而我们要查找的是所有的合法单词(每个合法单词都是不同的),也就是查找多个元素。在这点上,Hash是不适合作本题的查找数据结构的。不过,稍微利用一下Hash的特殊性质,这个问题就解决了。Hash需要设计Hash函数,而Hash函数是有不可避免的冲突的,如果被查找元素发生冲突,则可能找到多个目标元素,必须在多个目标元素中找出真正要查找的元素。我们正好可以抓住“冲突”这一点,利用这个“冲突”,设计一个比较特殊的Hash函数,让所有的合法单词的Hash函数值相同,即让所有合法单词“冲突”。这样,要找合法单词,只要计算一下任一合法单词对应的Hash函数值,然后在Hash表中把该值对应的所有冲突单词找出来即可。
现在我们就来设计这个Hash函数。其实这个函数说来也简单:首先确定一个搜索的顺序(即先搜索哪个空位,后搜索哪个空位),然后就可以确定搜索每个空位时该空位中被确定的字母的位置。
如图7-4,共有两个空位可填单词,(0, 1)~(2, 1)和(1, 0)~(1, 2)。假设先填(0, 1)~(2, 1),这时没有任何位置的字母被确定,所有长度为3的单词都是合法的单词。但是,填完第一个单词以后,对于空位(1, 0)~(1, 2)来说,就有一个位置的字母已经被确定下来了,它就是(1, 1)位置上的字母。
图7-4
|
正在上传…重新上传取消 | …… |
正在上传…重新上传取消 | …… |
正在上传…重新上传取消 |
图7-5
如图7-5,设一个长度为L的单词的第i1、i2、…in位上已经被确定下来,那么一种可以选择的Hash函数是
![]()
正在上传…重新上传取消
这里,p可以是任取的一个数(一般来说,p取质数效果比较好),HASHLEN是Hash表的长度(一般也是取质数效果较佳)。
设计完了Hash函数以后,一切的做法就一目了然了:首先确定一个搜索的顺序,根据每一步空位上确定的字母的位置,对每个单词按特定的Hash函数计算其Hash函数值,并将其放入Hash表(建议用“吊桶法”处理冲突),这是一个初始化的过程。然后,按前面定的顺序进行搜索(这个顺序最好是每次都选能确定字母数最多空位),根据确定的字母计算出合法单词对应的Hash函数值,并从Hash表中取出所有合法单词(当然,也可能会取出少量的非法单词,可以稍加判断将其去除),进行枚举。
算法的总体思想是利用Hash表来快速的查找合法单词,以达到可行性剪枝的目的。
最后,我们来简单分析一下算法的复杂性。由于使用了Hash表,复杂度是概率的,很难估算。需要指出的是,待选的单词表是一个词典,词典一般是正态分布的,所以除了搜索的第一层以外,以后的合法单词肯定都是很少的,再加上合法性剪枝的成分,实际上程序的效率应该是很高的。但是,这个算法毕竟还是指数级的,虽然使用了Hash表基本上把所有的无用功都去掉了(当然,还会有一些非法单词产生冲突,不过,当Hash表长度达到单词数的两倍以上后,这样的冲突概率一般都很小,基本可以忽略)。指数级的算法肯定不是一个完美的算法,所以如果数据非常强的话,这个算法也是有可能超时的,只是这样的数据很难出,至少现在还没能找出这样的数据来。
7.4 魔术数字游戏
| 源程序名 magic.???(pas, c, cpp) 可执行文件名 magic.exe 输入文件名 magic.in 输出文件名 magic.out |
【问题描述】
填数字方格的游戏有很多种变化,如下图所示的4×4方格中,我们要选择从数字1到16来填满这十六个格子(Aij,其中i=1..4,j=1..4)。为了让游戏更有挑战性,我们要求下列六项中的每一项所指定的四个格子,其数字累加的和必须为34:
四个角落上的数字,即A11+A14+A41+A44=34。
每个角落上的2×2方格中的数字,例如左上角:A11+A12+A21+A22=34。
最中间的2×2方格中的数字,即A22+A23+A32+A33=34。
每条水平线上四个格子中的数字,即Ai1+Ai2+Ai3+Ai4=34,其中i=1..4。
每条垂直线上四个格子中的数字,即A1j+A2j+A3j+A4j=34,其中j=1..4。
两条对角线上四个格子中的数字,例如左上角到右下角:A11+A22+A33+A44=34。
右上角到左下角:A14+A23+A32+A41=34
| A11 | A12 | A13 | A14 |
| A21 | A22 | A23 | A24 |
| A31 | A32 | A33 | A34 |
| A41 | A42 | A43 | A44 |
【输入】
输入文件会指定把数字1先固定在某一格内。输入的文件只有一行包含两个正数据I和J,表示第1行和第J列的格子放数字1。剩下的十五个格子,请按照前述六项条件用数字2到16来填满。
【输出】
把全部的正确解答用每4行一组写到输出文件,每行四个数,相邻两数之间用一个空格隔开。两组答案之间,要以一个空白行相间,并且依序排好。排序的方式,是先从第一行的数字开始比较,每一行数字,由最左边的数字开始比,数字较小的解答必须先输出到文件中。
【样例】
magic.in magic.out
1 1 1 4 13 16
14 15 2 3
8 5 12 9
11 10 7 6
1 4 13 16
14 15 2 3
12 9 8 5
7 6 11 10
【问题分析】
设方格中的16个数为16个未知数。根据题目给出的约束,可以列出16个方程。
四个角落上的数字:
A11+A14+A41+A44=34
每个角落上的2*2方格中的数字:
A11+A12+A21+A22=34
A13+A14+A23+A24=34
A31+A32+A41+A42=34
A33+A34+A43+A44=34
最中间的2*2方格中的数字:
A22+A23+A32+A33=34
每条水平线上四个格子中的数字:
Ai1+Ai2+Ai3+Ai4=34,其中i=1..4。
每条垂直线上四个格子中的数字:
A1j+A2j+A3j+A4j=34,其中j=1..4。
两条对角线上四个格子中的数字:
A11+A22+A33+A44=34
A14+A23+A32+A41=34
当然,这16个方程是有线性相关的,所以这个方程组是不定方程。解方程时,可能会出现自由未知量。不过,未知数的取值范围较小(1~16),所以可以通过枚举自由未知量的方法来求得所有解。
7.5 魔板
| 源程序名 panel.???(pas, c, cpp) 可执行文件名 panel.exe 输入文件名 panel.in 输出文件名 panel.out |
【问题描述】
有这样一种魔板:它是一个长方形的面板,被划分成n行m列的n*m个方格。每个方格内有一个小灯泡,灯泡的状态有两种(亮或暗)。我们可以通过若干操作使魔板从一个状态改变为另一个状态。操作的方式有两种:
(1)任选一行,改变该行中所有灯泡的状态,即亮的变暗、暗的变亮;
(2)任选两列,交换其位置。
当然并不是任意的两种状态都可以通过若干操作来实现互相转化的。
你的任务就是根据给定两个魔板状态,判断两个状态能否互相转化。
【输入】
文件中包含多组数据。第一行一个整数k,表示有k组数据。
每组数据的第一行两个整数n和m。(0<n,m≤100)
以下的n行描述第一个魔板。每行有m个数字(0或1),中间用空格分隔。若第x行的第y个数字为0,则表示魔板的第x行y列的灯泡为“亮”;否则为“暗”。
然后的n行描述第二个魔板。数据格式同上。
任意两组数据间没有空行。
【输出】
共k行,依次描述每一组数据的结果。
若两个魔板可以相互转化,则输出YES,否则输出NO。(注意:请使用大写字母)
【样例】
panel.in panel.out
2 YES
3 4 NO
0 1 0 1
1 0 0 1
0 0 0 0
0 1 0 1
1 1 0 0
0 0 0 0
2 2
0 0
0 1
1 1
1 1
【问题分析】
用改变第一个魔板的方法来得到第二个魔板。
枚举每一个列交换到第一列的情况。第一列确定以后,每一行是否应该变色也就确定下来了。然后再检查每一列是否与目标状态的每一列存在一一对应,如果存在一一对应,两个魔板就可以互相转化。
7.6 三维扫描
| 源程序名 scan.???(pas, c, cpp) 可执行文件名 scan.exe 输入文件名 scan.in 输出文件名 scan.out |
【问题描述】
工业和医学上经常要用到一种诊断技术——核磁共振成像(Magnetic Resonance Imagers)。利用该技术可以对三维物体(例如大脑)进行扫描。扫描的结果用一个三维的数组来保存,数组的每一个元素表示空间的一个像素。数组的元素是0~255的整数,表示该像素的灰度。例如0表示该像素是黑色的,255表示该像素是白色的。
![]()
正在上传…重新上传取消被扫描的物体往往是由若干个部件组合而成的。例如临床医学要对病变的器官进行检查,而器官是由一些不同的组织构成的。在实际问题中,同一个部件内部的色彩变化相对连续,而不同的部件的交界处色彩往往有突变。下图是一个简化的植物细胞的例子。
![]()
正在上传…重新上传取消
从细胞的平面图来看,该细胞大致是由四个“部件”构成的,细胞壁、细胞核、液泡和细胞质。为了方便起见,我们对部件的概念做如下的规定:
(1)如果一个像素属于某部件,则或者该像素至少与该部件的一个像素相邻,或者该像素单独组成一个部件。(说明:每一个像素与前后、左右、上下的6个像素相邻)
(2)同一个部件内部,相邻两个像素的灰度差不超过正整数M。M决定了程序识别部件的灵敏度。
请你编一个程序,对于给定的物体,判断该物体是由几个部件组成的。
【输入】
第一行是三个正整数L,W.H(L,W,H≤50),表示物体的长、宽、高。
第二行是一个整数M(0≤M≤255),表示识别部件的灵敏度。
接下来是L×W×H个O~255的非负整数,按照空间坐标从小到大的顺序依次给出每个像素的灰度。
说明:对于空间两点P1(x1, y1, z1)和P2(x2, y2, z2),P1<P2当切仅当
(x1<x2)或者(x1=x2且y1<y2)或者(x1=x2且y1=y2且z1<z2)s
【输出】
一个整数N,表示一共识别出几个部件。
【样例】
scan.in scan.out
2 2 2 2
0
1 1 1 1 2 2 2 2
【问题分析】
根据定义,如果相邻两个格子的颜色差小于M,那么它们属于同一个部件。利用flood fill,不断找出没有被fill的格子,flood fill得到与它同部件的所有格子,即分离出了一个部分。统计一下,就能得到部件数。
7.7 拼字游戏
| 源程序名 scrabble.???(pas, c, cpp) 可执行文件名 scrabble.exe 输入文件名 scrabble.in 输出文件名 scrabble.out |
【问题描述】
有一个未知的4×4的拼盘M,它的每个元素都是正整数。给出4行元素的总和,4列元素的总和以及两条对角线元素总和。另外还给出了拼盘中任意4个位置的元素值,它们的位置在输入文件中给定。
编写一个程序求出拼盘中另外12个位置的正整数的值,要求这些元素的行之和,列之和以及对角线之和与输入文件中给定的值相一致。
【输入】
输入文件包含用空格隔开的22个正整数。
前四个数字分别表示四行中每一行元素的总和,接下来的4个数字分别表示4列中每列元素的总和。接下来的数字表示主对角线元素的总和,即M(0, 0)+M(1,1)+M(2, 2)+M(3, 3)。然后的数字(第10个数字)表示逆对角线上元数之和,即M(0, 3)+M(1, 2)+M(2, 1)+M(3, 0)。剩下的部分还包含12个数字,被分成三个一组的形式i,j,k。表示M(i,j)=k。
你可以假设任何行对角线或列之和不会超过300。另外还可假设对于给定的输入文件总是存在解决方案。
【输出】
输出文件应包含按4×4的形式输出的16个数字,同一行的四个数字用一个空个隔开。注意:对于给定的输入文件,可能有一个以上可能的解决方案。任何一个方案都是可接受的。
【样例】
scrabble.in
130 120 172 140 157 93 144 168 66 195 0 1 15 1 3 49 2 2 16 3 0 33
scrabble.out
22 15 28 65
49 1 21 49
53 76 16 27
33 1 79 27
【问题分析】
设4×4的方格中的16个数为16个未知数。根据题目给的信息,我们知道其中4个未知数的值,也就是有了4个方程。此外,我们还知道4行4列和两条对角线的和,也就是10个方程。所以,加起来一共是12个方程。
显然,这个方程组是不定方程。解这个方程,会出现自由未知量,不过自由未知量的个数很少,并且都是300以内的整数,所以我们可以通过枚举自由未知量来求解不定方程组的解。
7.8 小木棍
| 源程序名 stick.???(pas, c, cpp) 可执行文件名 stick.exe 输入文件名 stick.in 输出文件名 stick.out |
【问题描述】
乔治有一些同样长的小木棍,他把这些木棍随意砍成几段,直到每段的长都不超过50。
现在,他想把小木棍拼接成原来的样子,但是却忘记了自己开始时有多少根木棍和它们的长度。
给出每段小木棍的长度,编程帮他找出原始木棍的最小可能长度。
【输入】
输入文件共有二行。
第一行为一个单独的整数N表示看过以后的小木柜的总数,其中N≤60,第二行为N个用空个隔开的正整数,表示N跟小木棍的长度。
【输出】
输出文件仅一行,表示要求的原始木棍的最小可能长度。
【样例】
stick.in stick.out
9 6
5 2 1 5 2 1 5 2 1
【问题分析】
搜索的顺序是枚举原始木棍的长度,从小到大或从大到小均可。但注意从大到小枚举的时候,可以剪枝,如果长度为k·L的原始木棍尝试失败的话,长度为L的就不必尝试了,因为必然也是失败的。
得到了原始木棍的长度后,一个一个的去枚举拼它的方案。注意,枚举要按字典序,举个例子说,就是不允许出现第一个木棍是由第2、5、6个小木棍拼成,而第二个木棍是由第1、3、4个小木棍拼成(2、5、6的字典序大于1、3、4)。
枚举的过程中,有一个比较强的剪枝:如果放入一个长度为len的小木棍后,正好拼成了一个原始长度的木棍,但是拼后面的木棍失败,那么就没有必要再枚举比len短的木棍了。因为一段整空间被一个刚好长度的木棍去填总是不亏的。(为方便起见,可以事先将小木棍降序排列)
7.9 单词游戏
| 源程序名 words.???(pas, c, cpp) 可执行文件名 words.exe 输入文件名 words.in 输出文件名 words.out |
【问题描述】
Io和Ao在玩一个单词游戏。
他们轮流说出一个仅包含元音字母的单词,并且后一个单词的第一个字母必须与前一个单词的最后一个字母一致。
游戏可以从任何一个单词开始。
任何单词禁止说两遍,游戏中只能使用给定词典中含有的单词。
游戏的复杂度定义为游戏中所使用的单词长度总和。
编写程序,求出使用一本给定的词典来玩这个游戏所能达到的游戏最大可能复杂度。
【输入】
输入文件的第一行,表示一个自然数N(1≤N≤16),N表示一本字典中包含的单词数量以下的每一行包含字典中的一个单词,每一个单词是由字母A、E、I、O和U组成的一个字符串,每个单词的长度将小于等于100,所有的单词是不一样的。
【输出】
输出文件仅有一行,表示该游戏的最大可能复杂度。
【样例】
words.in words.out
5 16
IOO
IUUO
AI
OIOOI
AOOI
【问题分析】
枚举要取的单词,如果这个单词构成的图存在欧拉路(不一定是回路),则存在一个单词接龙的方案,这些单词的长度和就是一个解。答案是所有解的最大值。算法的时间复杂度是O(2n·n),n≤16。
第八章 动态规划
8.1 字串距离
| 源程序名 blast.???(pas, c, cpp) 可执行文件名 blast.exe 输入文件名 blast.in 输出文件名 blast.out |
【问题描述】
设有字符串X,我们称在X的头尾及中间插入任意多个空格后构成的新字符串为X的扩展串,如字符串X为”abcbcd”,则字符串“abcb□cd”,“□a□bcbcd□”和“abcb□cd□”都是X的扩展串,这里“□”代表空格字符。
如果A1是字符串A的扩展串,B1是字符串B的扩展串,A1与B1具有相同的长度,那么我扪定义字符串A1与B1的距离为相应位置上的字符的距离总和,而两个非空格字符的距离定义为它们的ASCII码的差的绝对值,而空格字符与其他任意字符之间的距离为已知的定值K,空格字符与空格字符的距离为0。在字符串A、B的所有扩展串中,必定存在两个等长的扩展串A1、B1,使得A1与B1之间的距离达到最小,我们将这一距离定义为字符串A、B的距离。
请你写一个程序,求出字符串A、B的距离。
【输入】
输入文件第一行为字符串A,第二行为字符串B。A、B均由小写字母组成且长度均不超过2000。第三行为一个整数K(1≤K≤100),表示空格与其他字符的距离。
【输出】
输出文件仅一行包含一个整数,表示所求得字符串A、B的距离。
【样例】
blast.in blast.out
cmc 10
snmn
2
【算法分析】
字符串A和B的扩展串最大长度是A和B的长度之和。如字符串A为“abcbd”,字符串B为“bbcd”,它们的长度分别是la=5、lb=4,则它们的扩展串长度最大值为LA+LB=9,即A的扩展串的5个字符分别对应B的扩展串中的5个空格,相应B的扩展串的4个字符对应A的扩展串中的4个空格。例如下面是两个字符串的长度为9的扩展串:
a□b c□b□d□
□b□□b□c□d
而A和B的最短扩展串长度为la与lb的较大者,下面是A和B的长度最短的扩展串:
a b cbd
b□bcd
因此,两个字符串的等长扩展串的数量是非常大的,寻找最佳“匹配”(对应位置字符距离和最小)的任务十分繁重,用穷举法无法忍受,何况本题字符串长度达到2000,巨大的数据规模,势必启发我们必须寻求更有效的方法:动态规划。
记<A1, A2, …, Ai>为A串中A1到Ai的一个扩展串,<B1, B2, …, Bj>为B串中B1到Bj的一个扩展串。这两个扩展串形成最佳匹配的条件是(1)长度一样;(2)对应位置字符距离之和最小。
首先分析扩展串<A1, A2, …, Ai>与扩展串<B1, B2, …, Bj>长度一样的构造方法。扩展串<A1, A2, …, Ai>与扩展串<B1, B2, …, Bj>可以从下列三种情况扩张成等长:
(1)<A1, A2, …, Ai>与<B1, B2, …, Bj-1>为两个等长的扩展串,则在<A1, A2, …, Ai>后加一空格,<B1, B2, …, Bj-1>加字符Bj;
(2)<A1, A2, …, Ai-1>与<B1, B2, …, Bj>为两个等长的扩展串,则在<A1, A2, …, Ai-1>添加字符Ai,在<B1, B2, …, Bj>后加一空格;
(3)<A1, A2, …, Ai-1>与<B1, B2, …, Bj-1>为两个等长的扩展串,则在<A1, A2, …, Ai-1>后添加字符Ai,在<B1, B2, …, Bj-1>后添加字符Bj。
其次,如何使扩展成等长的这两个扩展串为最佳匹配,即对应位置字符距离之和最小,其前提是上述三种扩展方法中,被扩展的三对等长的扩展串都应该是最佳匹配,以这三种扩展方法形成的等长扩展串(A1, A2, …, Ai>和<B1, B2, …, Bj>也有三种不同情形,其中对应位置字符距离之和最小的是最佳匹配。
为了能量化上述的构造过程,引入记号g[i, j]为字符串A的子串A1, A2, …, Ai与字符串B的子串B1, B2, …, Bj的距离,也就是扩展串<A1, A2, …, Ai>与扩展串<B1, B2, …, Bj>是一个最佳匹配。则有下列状态转移方程:
g[i, j]=Min{g[i-1, j]+k, g[i, j-1]+k, g[i-1, j-1]+
![]()
正在上传…重新上传取消} 0≤i≤La 0≤j≤Lb
其中,k位字符与字符之间的距离;
![]()
正在上传…重新上传取消为字符ai与字符bi的距离。
初始值:g[0, 0]=0 g[0, j]=j·k g[i, 0]=i·k
综上所述,本题的主要算法如下:
(1)数据结构
var a, b:array[1..2000]of byte; {以ASCII码表示的字符串}
g:array[0..2000, 0..2000]of longint; {各阶段的匹配距离}
(2)读入字符串A、B,转换为ASCII码
la:=0; lb:=0;
while not(eoln(f)) do {子串长度单元}
begin {从文件中读入一行字符}
read(f, c);
inc(la);
a[la]:=ord(c);
end;
readln(f);
while not(eoln(f)) do
begin
read(f, c);
inc(lb);
b[lb]:=ord(c);
end;
readln(f);
(3)根据状态转移方程求g[la, lb]
g[0, 0]:=0;
for i:=1 to la do g[i, 0]:=k+g[i-1, 0];
for j:=1 to lb do g[0, j]:=k+g[0, j-1];
for i:=1 to la do
for j:=1 to lb do
begin
g[i, j]:=k+g[i-1,j];
temp:=g[i, j-1]+k;
if g[i, j]>temp then g[i, j]:=temp;
temp:=g[i-1,j-1]+abs(a[i]-b[j]);
if g[i, j]>temp then g[i, j]:=temp;
end;
(4)输出
writeln(f, g[la, lb]);
8.2 血缘关系
| 源程序名 family.???(pas, c, cpp) 可执行文件名 family.exe 输入文件名 family.in 输出文件名 family.out |
【问题描述】
我们正在研究妖怪家族的血缘关系。每个妖怪都有相同数量的基因,但是不同的妖怪的基因可能是不同的。我们希望知道任意给定的两个妖怪之间究竟有多少相同的基因。由于基因数量相当庞大,直接检测是行不通的。但是,我们知道妖怪家族的家谱,所以我们可以根据家谱来估算两个妖怪之间相同基因的数量。
妖怪之间的基因继承关系相当简单:如果妖怪C是妖怪A和B的孩子,则C的任意一个基因只能是继承A或B的基因,继承A或B的概率各占50%。所有基因可认为是相互独立的,每个基因的继承关系不受别的基因影响。
现在,我们来定义两个妖怪X和Y的基因相似程度。例如,有一个家族,这个家族中有两个毫无关系(没有相同基因)的妖怪A和B,及它们的孩子C和D。那么C和D相似程度是多少呢?因为C和D的基因都来自A和B,从概率来说,各占50%。所以,依概率计算C和D平均有50%的相同基因,C和D的基因相似程度为50%。需要注意的是,如果A和B之间存在相同基因的话,C和D的基因相似程度就不再是50%了。
你的任务是写一个程序,对于给定的家谱以及成对出现的妖怪,计算它们之间的基因相似程度。
【输入】
第一行两个整数n和k。n(2≤n≤300)表示家族中成员数,它们分别用1, 2, …, n来表示。k(0≤k≤n-2)表示这个家族中有父母的妖怪数量(其他的妖怪没有父母,它们之间可以认为毫无关系,即没有任何相同基因)。
接下来的k行,每行三个整数a, b, c,表示妖怪a是妖怪b的孩子。
然后是一行一个整数m(1≤m≤n2),表示需要计算基因相似程度的妖怪对数。
接下来的m行,每行两个整数,表示需要计算基因相似程度的两个妖怪。
你可以认为这里给出的家谱总是合法的。具体来说就是,没有任何的妖怪会成为自己的祖先,并且你也不必担心会存在性别错乱问题。
【输出】
共m行。可k行表示第k对妖怪之间的基因相似程度。你必须按百分比输出,有多少精度就输出多少,但不允许出现多余的0(注意,0.001的情况应输出0.1%,而不是.1%)。具体格式参见样例。
【样例】
family.in family.out
7 4 0%
4 1 2 50%
5 2 3 81.25%
6 4 5 100%
7 5 6
4
1 2
2 6
7 5
3 3
【知识准备】
(1)基本的概率计算知识;
(2)递推原理(包括记忆化搜索)。
【算法分析】
本题是一道概率计算题,但这个概率计算又是建立在Family Tree模型上的。Family Tree是一个有向无环图,有明显的阶段性(辈分关系),而且没有后效性(没有人可以成为自己的祖先),符合动态规划模型的基本条件。因此,应该可以套用类似动态规划的方法来解决。
我们先来明确一下相似程度的计算方法。假设我们要求的是A和B的相似程度(设为P(A, B)),那么有两种情况是显然的:
(1)A=B:P(A, B)=1;
(2)A与B无相同基因:P(A, B)=0。
这是计算其他复杂情况的基础。因为动态规划就是从一些特定的状态(边界条件)出发,分阶段推出其他状态的值的。
再来看一般的情况,设A0和A1是A的父母。那么,取概率平均情况,A拥有A0和A1的基因各占一半。假设A0与B的相似程度为P(A0, B),A1与B的相似程度为P(A1, B),那么P(A, B)与P(A0, B)和P(A1, B)之间应该是一个什么样的关系呢?很容易猜想到:
P(A, B)=(P(A0, B)+P(A1, B))/2
但是,这只是一个猜想。要让它变为一个结论还需要证明:
我们用归纳法来证明。
首先,我们知道,在这个问题中不同基因都是从特定的祖先传下来的,不会出现同一个基因采自不同的祖先的情况(注:这里的祖先是指那些没有父母的妖怪)。所以,如果A与B有相同的基因,这些基因必然来自同一个祖先。这里,我们最想说明的是,祖先那代是不存在两个人,它们之间不同的基因相同的概率不一样,因为它们相同的概率都是0。
现在,A有祖先A0和A1,A0和A1与B的相似程度分别为P(A0, B)和P(A1, B)。从祖先一代开始归纳,可由归纳假设A0与B、A1与B之间每个基因相同的概率都是一样的,分别都是P(A0, B)和P(A1, B)。A的单个基因,它可能是继承A0的,也可能是继承A1的,概率各50%。继承A0的话与B相同的概率是P(A0, B),继承A1的话与B相同的概率是P(A1, B)。那么这个基因与B相同的概率就是:
(P(A0, B)+P(A1, B))/2
因此,A的每个基因与B相同的概率都是(P(A0, B)+P(A1, B))/2,具有相同的概率。进而,A与B相同基因的数量概率平均也为(P(A0, B)+P(A1, B))/2,A与B的相似程度 P(A, B)=(P(A0, B)+P(A1, B))/2
这样就归纳证明了P(A, B)的概率递推公式。
下面总结一下前面得出的结论:
(1)边界条件:
① A=B:P(A, B)=1;
② A与B无相同基因:P(A, B)=0;
(2)递推关系:
P(A, B)=(P(A0, B)+P(A1, B))/2,其中A0和A1是A的父母
有了边界条件和递推关系,以及Family Tree的阶段性和无后效性作为前提,用动态规划解决问题的所有条件都已满足。应该说,从理论上来讲,本题已经完全解决。下面需要讨论的仅仅是实现方法而已。
动态规划的实现方法有两种:一种是逆向的递推,另一种是正向的记忆化搜索(递归)。这两种方法都是可行的,区别仅仅在于,递推需要更多的考虑状态的阶段性,按照阶段计算出所有状态的值;而记忆化搜索只需要承认状态具有阶段性,无需考虑阶段,只需要按照递推式本身设计带记忆化的递归函数即可。
本题给出的仅仅是一棵Family Tree,并没有给出Family Tree的阶段,如果要用递推的话,就必须先给Family Tree分阶段(拓扑排序)。所以,本题显然更适合用记忆化搜索来实现。
另外,需要注意的是,本题所求的答案是有多少精度就输出多少精度。300个节点的图,少说也可以构成几十层的Family Tree,算出的结果至少也有小数点后几十位。所以,高精度是必不可少的(保险起见,可以设置300位的高精度)。
分析一下本题的时间复杂度。动态规划的状态有n2个,转移代价为O(C)(高精度计算的代价)。因此,时间复杂度为为O(Cn2),n≤300。
严格的讲,本题的算法不能算动态规划的方法,因为本题不存在最优化,应该仅仅是一个递推。不过,从分析问题的过程来看,它里面包含了很多动态规划的思想,例如,阶段性和无后效性,特别是使用了动态规划的一种实现方法记忆化搜索。
8.3 尼克的任务
| 源程序名 lignja.???(pas, c, cpp) 可执行文件名 lignja.exe 输入文件名 lignja.in 输出文件名 lignja.out |
【问题描述】
尼克每天上班之前都连接上英特网,接收他的上司发来的邮件,这些邮件包含了尼克主管的部门当天要完成的全部任务,每个任务由一个开始时刻与一个持续时间构成。
尼克的一个工作日为N分钟,从第一分钟开始到第N分钟结束。当尼克到达单位后他就开始干活。如果在同一时刻有多个任务需要完戍,尼克可以任选其中的一个来做,而其余的则由他的同事完成,反之如果只有一个任务,则该任务必需由尼克去完成,假如某些任务开始时刻尼克正在工作,则这些任务也由尼克的同事完成。如果某任务于第P分钟开始,持续时间为T分钟,则该任务将在第P+T-1分钟结束。
写一个程序计算尼克应该如何选取任务,才能获得最大的空暇时间。
【输入】
输入数据第一行含两个用空格隔开的整数N和K(1≤N≤10000,1≤K≤10000),N表示尼克的工作时间,单位为分钟,K表示任务总数。
接下来共有K行,每一行有两个用空格隔开的整数P和T,表示该任务从第P分钟开始,持续时间为T分钟,其中1≤P≤N,1≤P+T-1≤N。
【输出】
输出文件仅一行,包含一个整数,表示尼克可能获得的最大空暇时间。
【样例】
lignja.in lignja.out
15 6 4
1 2
1 6
4 11
8 5
8 1
11 5
【算法分析】
题目给定的数据规模十分巨大:1≤K≤10000。采用穷举方法显然是不合适的。根据求最大的空暇时间这一解题要求,先将K个任务放在一边,以分钟为阶段,设置minute[i]表示从第i分钟开始到最后一分钟所能获得的最大空暇时间,决定该值的因素主要是从第i分钟起到第n分钟选取哪几个任务,与i分钟以前开始的任务无关。由后往前逐一递推求各阶段的minute值:
(1)初始值minute[n+1]=0
(2)对于minute[i],在任务表中若找不到从第i分钟开始做的任务,则minute[i]比minute[i+1]多出一分钟的空暇时间;若任务表中有一个或多个从第i分钟开始的任务,这时,如何选定其中的一个任务去做,使所获空暇时间最大,是求解的关键。下面我们举例说明。
设任务表中第i分钟开始的任务有下列3个:
任务K1 P1=i T1=5
任务K2 P2=i T2=8
任务K3 P3=i T3=7
而已经获得的后面的minute值如下:
minute[i+5]=4,minute[i+8]=5,minute[i+7]=3
若选任务K1,则从第i分钟到第i+1分钟无空暇。这时从第i分钟开始能获得的空暇时间与第i+5分钟开始获得的空暇时间相同。因为从第i分钟到i+5-1分钟这时段中在做任务K1,无空暇。因此,minute[i]=minute[i+5]=4。
同样,若做任务K2,这时的minute[i]=minute[i+8]=5
若做任务K3,这时的minute[i]=minute[1+7]=3
显然选任务K2,所得的空暇时间最大。
因此,有下面的状态转移方程:
![]()
正在上传…重新上传取消
其中,Tj表示从第i分钟开始的任务所持续的时间。
下面是题目所给样例的minute值的求解。
| 任务编号K | 1 | 2 | 3 | 4 | 5 | 6 |
| 开始时间P | 1 | 1 | 4 | 8 | 8 | 11 |
| 持续时间T | 2 | 6 | 11 | 5 | 1 | 5 |
| 时刻I | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| minute[i] | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 |
| 选任务号k | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 4 | 0 | 0 | 0 | 3 | 0 | 0 | 2 |
注:选任务号为该时刻开始做的任务之一,0表示无该时刻开始的任务。
问题所求得最后结果为从第1分钟开始到最后时刻所获最大的空暇时间minute[1]。
主要算法描述如下:
(1)数据结构
var p:array[1..10000]of integer; {任务开始时间}
t:array[1..10000]of integer; {任务持续时间}
minute:array[0..10001]of integer; {各阶段最大空暇时间}
(2)数据读入
① readln(n, k); {读入总的工作时间n及任务k}
② 读入k个任务信息
for i:=1 to k do readln(p[i],t[i]); {假设任务的开始时间按有小到大排列}
(3)递推求minute[i]
j:=k; {从最后一个任务选起}
for i:=n downto 1 do
begin
minute[i]:=0;
if p[i]<>i then minute[i]:=1+minute[i+1] {无任务可选}
else while p[j]=i do {有从i分钟开始的任务}
begin
if minute[i+t[j]]>minute[i] then minute[i]:=minute[i+t[j]]; {求最大空暇时间}
j:=j-1; {下一个任务}
end;
end;
(4)输出解
writeln(minute[1]);
8.4 书的复制
| 源程序名 book.???(pas, c, cpp) 可执行文件名 book.exe 输入文件名 book.in 输出文件名 book.out |
【问题描述】
现在要把m本有顺序的书分给k给人复制(抄写),每一个人的抄写速度都一样,一本书不允许给两个(或以上)的人抄写,分给每一个人的书,必须是连续的,比如不能把第一、第三、第四本书给同一个人抄写。
现在请你设计一种方案,使得复制时间最短。复制时间为抄写页数最多的人用去的时间。
【输入】
第一行两个整数m,k;(k≤m≤500)
第二行m个整数,第i个整数表示第i本书的页数。
【输出】
共k行,每行两个整数,第i行表示第i个人抄写的书的起始编号和终止编号。k行的起始编号应该从小到大排列,如果有多解,则尽可能让前面的人少抄写。
【样例】
book.in book.out
9 3 1 5
1 2 3 4 5 6 7 8 9 6 7
8 9
【问题分析】
本题可以用动态规划解决,但是动态规划并不是一个聪明的方法,这个后面会提到。不管怎样,我们还是先介绍动态规划的方法。
设f(n, k)为前n本书交由k个人抄写,需要的最短时间,则状态转移方程为
f(n, k)=min{max{f(i, k-1),
![]()
正在上传…重新上传取消}, i=1, 2, …, n-1}
状态数为n·k,转移代价为O(n),故时间复杂度为O(n2·k)。
不难看出,上述方程满足四边形不等式,所以如果利用四边形不等式的性质,转移代价由平摊分析可得平均为O(1)。因此,时间复杂度可以降为O(n·k)。
动态规划求出的仅仅是最优值,如果要输出具体方案,还需根据动态规划计算得到的最优值,做一个贪心设计。具体来说,设最优值为T,那么k个人,每个人抄写最多T页。按顺序将书分配给k人去抄写,从第一个人开始,如果他还能写,就给他;否则第一个人工作分配完毕,开始分配第二个人的工作;以后再是第三个、第四个、……直至第k个。一遍贪心结束后,具体的分配方案也就出来了。贪心部分的复杂度是O(n)的。
从前面的分析可以看到,动态规划部分仅仅是求出了一个最优值,具体方案是通过贪心求得的。而动态规划这部分的时间复杂度却是相当之高,所以用动态规划来求最优值是很不合算的。可以看到,当每人抄写的页数T单调增加时,需要的人数单调减少,这就符合了二分法的基本要求。我们可以对T二分枚举,对每个枚举的T,用贪心法既求出需要的人数又求出具体的方案。所以,通过二分就能求得需要人数为k的最小的Tmin和相应的方案了。时间复杂度为O(nlog2c),c为所有书本的页数和。
从这道题目的解题过程中,我们可以看到动态规划也不是万金油,有时更一般的方法却可以得到更好的结果。
8.5 多米诺骨
| 源程序名 dom.???(pas, c, cpp) 可执行文件名 dom.exe 输入文件名 dom.in 输出文件名 dom.out |
【问题描述】
多米诺骨牌有上下2个方块组成,每个方块中有1~6个点。现有排成行的n个多米诺骨牌如图8-1所示。
| ● ● ● ● ● ● | ● | ● | ● | |||
| ● | ● ● ● ● ● | ● ● ● | ● ● |
上方块中点数之和记为
![]()
正在上传…重新上传取消,下方块中点数之和记为,它们的差为。例如在图8-1中,=6+1+1+1=9,=1+5+3+2=11,=2。每个多米诺骨牌可以旋转180°,使得上下两个方块互换位置。
编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。
对于图8-1中的例子,只要将最后一个多米诺骨牌旋转180°,可使上下2行点数之差为0。
【输入】
输入文件的第一行是一个正整数n(1≤n≤1000),表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数,表示多米诺骨牌上下方块中的点数a和b,且1≤a,b≤6。
【输出】
输出文件仅一行,包含一个整数。表示求得的最小旋转次数。
【样例】
dom.in dom.out
4 1
6 1
1 5
1 3
1 2
【问题分析】
本问题可归约为经典的背包问题。
假设一个骨牌的点数差的绝对值是s,那么它实际可以取到的点数差就是-s或s。我们不妨对取值进行一下平移,让每个骨牌可以取到的点数差为0和2s。这样,骨牌的“取正值还是负值”就转化为背包的“取与不取”了。
那么,我们求解的目标会怎样变化呢?本来,我们的目标是让取值的总和为0。现在,我们对每个骨牌的取值作了平移,平移的距离为s。那么,最后的取值总和就应该是∑s,即所有骨牌的平移距离之和。
8.6 平板涂色
| 源程序名 paint.???(pas, c, cpp) 可执行文件名 paint.exe 输入文件名 paint.in 输出文件名 paint.out |
【问题描述】
CE数码公司开发了一种名为自动涂色机(APM)的产品。它能用预定的颜色给一块由不同尺寸且互不覆盖的矩形构成的平板涂色。
![]()
正在上传…重新上传取消 ──→x 0 1 2 3 4 5 6
| Blue (A) | Red (B) | |
| Red (D) | Blue (E) | |
| Blue (C) | ||
| Red (G) | ||
| Blue (F) | ||
为了涂色,APM需要使用一组刷子。每个刷子涂一种不同的颜色C。APM拿起一把有颜色C的刷子,并给所有颜色为C且符合下面限制的矩形涂色:
为了避免颜料渗漏使颜色混合,一个矩形只能在所有紧靠它上方的矩形涂色后,才能涂色。例如图中矩形F必须在C和D涂色后才能涂色。注意,每一个矩形必须立刻涂满,不能只涂一部分。
写一个程序求一个使APM拿起刷子次数最少的涂色方案。注意,如果一把刷子被拿起超过一次,则每一次都必须记入总数中。
【输入】
文件paint.in第一行为矩形的个数N。下面有N行描述了N个矩形。每个矩形有5个整数描述,左上角的y坐标和x坐标,右下角的y坐标和x坐标,以及预定颜色。
颜色号为1到20的整数。
平板的左上角坐标总是(0, 0)。
坐标的范围是0..99。
N小于16。
【输出】
输出至文件paint.out,文件中记录拿起刷子的最少次数。
【样例】
paint.in paint.out
7 3
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2
【问题分析】
指数型动态规划。
由于N小于16,故可以以一个N-bit的二进制数A作为状态,其中每个二进制位表示一个格子的涂色情况,二进制位0表示该格子未被涂色,二进制1表示该格子已被涂色。
用F[A]表示要得到状态A,最少需要改变多少次颜色。对于每个状态A,通过枚举涂色方案来推新的状态。
8.7 三角形牧场
| 源程序名 pasture.???(pas, c, cpp) 可执行文件名 pasture.exe 输入文件名 pasture.in 输出文件名 pasture.out |
【问题描述】
和所有人一样,奶牛喜欢变化。它们正在设想新造型的牧场。奶牛建筑师Hei想建造围有漂亮白色栅栏的三角形牧场。她拥有N(3≤N≤40)块木板,每块的长度Li(1≤Li≤40)都是整数,她想用所有的木板围成一个三角形使得牧场面积最大。
请帮助Hei小姐构造这样的牧场,并计算出这个最大牧场的面积。
【输入】
第1行:一个整数N
第2..N+1行:每行包含一个整数,即是木板长度。
【输出】
仅一个整数:最大牧场面积乘以100然后舍尾的结果。如果无法构建,输出-1。
【样例】
pasture.in pasture.out
5 692
1
1
3
3
4
【样例解释】
692=舍尾后的(100×三角形面积),此三角形为等边三角形,边长为4。
【问题分析】
二维的背包问题。
将所有的木板当作背包,木板的长度作为背包的重量。与普通背包问题不同的是,这里有两个背包。所以,我们要求的不是重量w是否能得到,而是一个重量二元组(w0, w1)是否能得到。求解的方法与普通背包问题基本相同,只不过状态是二维的。
求得所有可以得到的二元组后,枚举所有的二元组。对于任意的(w0, w1),w0, w1,w—w0—w1(w表示所有背包的总重量)即是对应的三角形三边之长(可能是非法三角形)。这些三角形中面积最大者就是我们所求的答案。
8.8 分组
| 源程序名 teams.???(pas, c, cpp) 可执行文件名 teams.exe 输入文件名 teams.in 输出文件名 teams.out |
【问题描述】
你的任务是把一些人分成两组,使得:
·每个人都被分到其中一组;
·每个组都至少有一个人;
·一组中的每个人都认识其他同组成员;
·两组的成员人数近两接近。
这个问题可能有多个解决方案,你只要输出任意一个即可,或者输出这样的分组法不存在。
【输入】
为了简单起见,所有的人都用一个整数标记,每个人号码不同,从1到N。
输入文件的第一行包括一个整数N(2≤N≤100),N就是需要分组的总人数;接下来的N行对应了这N个人,按每个人号码的升序排列,每一行给出了一串号码Aij(1≤Aij≤N,Aij≠i),代表了第i个人所认识的人的号码,号码之间用空格隔开,并以一个“0”结束。
【输出】
如果分组方法不存在,就输出信息“No solution”(输出时无需加引号)至输出文件;否则用两行输出分组方案;第一行先输出第一组的人数,然后给出第一组成员的号码,每个号码前有一个空格,同理给出第二组的信息。每组的成员号码顺序和组别顺序并不重要。
【样例】
teams.in teams.out
5 3 1 3 5
2 3 5 0 2 2 4
1 4 5 3 0
1 2 5 0
1 2 3 0
4 3 2 1 0
【问题分析】
首先,确定这样的一组集合(Ai, Bi),集合Ai中的人必须和集合Bi的人分在不同组。这些集合可通过人与人之间认识与不认识的关系得到。
得到这些集合对后,问题就转化为一个背包问题了——即如何分配这些二元组,使得两边人数差尽量小。这个背包问题可以通过“平移”的方法转化为普通的背包问题。
第九章 数学问题
9.1 多项式展开系数
| 源程序名 equal.???(pas, c, cpp) 可执行文件名 equal.exe 输入文件名 equal.in 输出文件名 equal.out |
【问题描述】
二项式展开系数大家已经十分熟悉了:
![]()
正在上传…重新上传取消
现在我们将问题推广到任意t个实数的和的n次方(x1+x2+…+xt)n的展开式。我们想知道多项式(x1+x2+…+xt)n中的任意一项
![]()
正在上传…重新上传取消的系数。例如,将一个三项式(x1+x2+x3)3展开后,可以得到:
(x1+x2+x3)3=
![]()
正在上传…重新上传取消+++++++++ 其中,的系数为3
【输入】
第一行,两个整数n和t,中间用空格分隔。分别表示多项式幂和项数。
第二行,t个整数n1, n2, …, nt,中间用空格分隔。分别表示x1, x2, …, xn的幂。(n1+n2+…+nt=n,1≤n, t≤12)
【输出】
仅一行,一个整数(保证在长整型范围内)。表示多项式(x1+x2+…+xt)n中的项
![]()
正在上传…重新上传取消的系数。
【样例】
equal.in equal.out
3 3 3
2 1 0
【知识准备】
组合数运算; 二项式展开; 代数式的恒等变形。
【算法分析】
(1)利用二项式展开公式
![]()
正在上传…重新上传取消推广到多项式的展开:
![]()
正在上传…重新上传取消
其中含有
![]()
正在上传…重新上传取消的一项即为上式右边展开后的一项:
![]()
正在上传…重新上传取消
整理得到:
![]()
正在上传…重新上传取消 ①
所以要想求(x1+x2+…+xt)n 的任意一项
![]()
正在上传…重新上传取消的系数只要将①式中令x1=x2=…=xt=1,得到
(2)因为
![]()
正在上传…重新上传取消
![]()
正在上传…重新上传取消
……
![]()
正在上传…重新上传取消
![]()
正在上传…重新上传取消
所以
![]()
正在上传…重新上传取消
(3)由分析(1)、(2)求
![]()
正在上传…重新上传取消的系数化为求上述的除法运算:
① 先计算n!;
② 将n!逐一去除n1, n2, …, nt;
③ 最后的商为所求结果。
由于题目所给n≤12,计算n!可在长整型范围内,无需采用高精度运算。
设数组no:array[1..t]为nt;total为n!。主要算法描述如下
total:=1;
for i:=1 to n do total:=total+i; {求n!}
for i:=1 to t do
for j:=1 to no[i] do
9.2 两数之和
| 源程序名 pair.???(pas, c, cpp) 可执行文件名 pair.exe 输入文件名 pair.in 输出文件名 pair.out |
【问题描述】
我们知道从n个非负整数中任取两个相加共有n*(n-1)/2个和,现在已知这n*(n-1)/2个和值,要求n个非负整数。
【输入】
输入文件仅有一行,包含n*(n-1)/2+1个空格隔开的非负整数,其中第一个数表示n(2<n<10),其余n*(n-1)/2个数表示和值,每个数不超过100000。
【输出】
输出文件仅一行,按从小到大的次序依次输出一组满足要求的n个非负整数,相邻两个整数之间用一个空格隔开;若问题无解则输出“Impossible”。
【样例】
pair.in pair.out
3 1269 1160 1663 383 777 886
【算法分析】
本题的规模只有10,看似一道搜索题。其实不然,搜索固然有可能出解,但是本题是有多项式级算法的。本题的难点就在于要理清这看似混乱的n(n-1)/2个“和”的关系,从中寻找突破口。
那么,突破口在哪里呢?n(n-1)/2个“和”是任意给出的,并未按照什么指定的顺序,所以从表面上看这些数(和)之间似乎没有什么区别。当然,我们必须在这些数(和)中制造出一些区别来,因为没有区别我们也就无从下手。对什么信息也没有的一些数,惟一可以制造出的区别就是它们之间的大小关系。根据数的大小关系,我们可以对这n(n-1)/2个数排序。排完序后,可以成为突破口的无非就是那么几个,最小的数(和)、最大的数(和)、中位数……我们不可能随便找一个数出来作为突破口,因为随便找一个数的话,大小关系就失去意义了。所以,这时我们需要注意的只有这么几个数了:最小的数(和)、最大的数(和)和中位数。
中位数看上去似乎也很难成为突破口,因为我们无法预知中位数是哪两个数的和。而最小、最大的两个数(“最小的和”与“最大的和”)则不同,最小的和必然是最小的两个数之和,最大的和必然是最大的两个数之和。由问题对称性,最小与最大其实是等价的,所以我们可以只考虑最小的情况,解决了最小,最大也就相应解决了。
最小的和是最小的两个数之和,这是一条已经确定的与最小的两个数相关的信息。当然,就凭这些信息,我们还是无法知道最小的两个数究竟是多少,这是我们目前面临的一个障碍。我们不妨先跳过这个障碍,考虑以后的问题。我们可以假设已经知道最小的数的大小,这样我们又可以很顺利的知道次小的数是多少了(最小的和-最小的数)。
知道最小的两个数的大小对我们有什么好处呢?其实关键是知道最小的数是多少,这是至关重要的,因为很多特殊的和都与最小的数有关。试想,我们知道了最小的两个数,也就确定了一个和(最小的和)。把这个“和”从n(n-1)/2个和中去掉,剩下的n(n-1)/2-1个和中又会产生新的最小的和。这个新的最小的和是哪两个数的和呢?应该是最小的数与第三小的数的和。由于我们假设已经知道最小的数,我们自然就可以通过作差得到第三小的数了。
得到前三小的数后,我们就确定了3个“和”了。籽这三个“和”从n(n-1)/2个和中去掉,剩下的n(n-1)/2-3个和中又会产生新的最小的和。这个新的最小的和必然是最小的数与第四小的数的和。由于最小的数已知,第四小的数就可以算出了。
更一般的情况,知道了前k小的数,那么我们就确定了k(k-1)/2个和了。将这k(k-1)/2个和从n(n-1)/2个和中去掉,剩下的n(n-1)/2-k(k-1)/2个和中又会产生新的最小的和。这个新的最小的和必然是最小的数与第k+1小的数的和。由于最小的数已知,第k+1小的数就可以通过作差得到。
如此,在知道了最小的数的情况下,不断的从当前最小的和入手,就可以从小到大依次把所有的数都推算出来了。
不过,有一点还是需要注意的,前面所有的推导都是建立在最小的数已知的情况下的,但实际情况是最小的数未知。所以,我们还需要创造条件,使最小的数由未知变为已知。
一个简单而可行的方法就是枚举最小的数。简单就不必说了,为什么说枚举是可行的呢?因为题目规定所有的数都不超过100000,因此总共需要枚举的方案数最多只有100000。而在知道最小的数的情况下,推算出其他数的代价是O(n2),n≤10。100000*102的计算代价是可以承受的。
最后,我们总结一下前面得到的算法。
(1)枚举最小的数;
(2)根据最小的数和最小的和,得到次小的数;
(3)由前k小的数推出第k+1小的数。
算法的时间复杂度是O(Cn2),其中C表示数值的大小。
从本题的解题过程中,我们看到其中最关键的一步就是以最小的和作为突破口。在解决数学问题的时候,很多情况下从为数不多的信息中寻找突破口是至关重要的。找到了突破口,问题本身也就迎刃而解了。
9.3 盒子与球
| 源程序名 box.???(pas, c, cpp) 可执行文件名 box.exe 输入文件名 box.in 输出文件名 box.out |
【问题描述】
现有r个互不相同的盒子和n个互不相同的球,要将这n个球放入r个盒子中,且不允许有空盒子。问有多少种方法?
例如:有2个不同的盒子(分别编为1号和2号)和3个不同的球(分别编为1、2、3号),则有6种不同的方法:
| 1号盒子 | 1号球 | 1、2号球 | 1、3号球 | 2号球 | 2、3号球 | 3号球 |
| 2号盒子 | 2、3号球 | 3号球 | 2号球 | 1、3号球 | 1号球 | 1、2号球 |
【输入】
两个整数,n和r,中间用空格分隔。(0≤n, r≤10)
【输出】
仅一行,一个整数(保证在长整型范围内)。表示n个球放入r个盒子的方法。
【样例】
box.in
3 2
box.out
6
【知识准备】
第二类Stirling数。
【算法分析】
先考虑三种情况:
(1)若盒子数r大于球数n,根据题意不允许有空盒的要求,放置的方法数为零;
(2)若r=1,则只有一种放法;
(3)若r=n,相当于将n个不同的球进行排列,故有n!种。
下面考虑1<r<n的情况。
n个不同的球放入r个不同的盒子中,可以先把r个盒子视为相同的,即先求出n个不同的球放入r个相同的盒子中,且不允许有空盒子的不同方案数,设为S(n, r);再将r个盒子进行全排列,共有r!。
记号f(n, r)为n个不同的球放入r个不同盒子中,且不允许有空盒子的不同放法,根据乘法原理,有f(n, r)=S(n, r)·r!
如何求S(n, r)?请看如下定义:
定义 n个有区别的球放入r个相同的盒子中,要求无一空盒,其不同的方案数s(n, r)称为第二类Stirling数。
例如:红(k)、黄(y)、蓝(b)、白(w)四种颜色的球,放入两个无区别的盒子里,不允许空盒,其方案数共有如下7种:
| 方案 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 第1盒子 | r | y | b | w | ry | rb | rw |
| 第2盒子 | ybw | rbw | ryw | ryb | bw | yw | yb |
所以S(4, 2)=7
下面就1≤n≤5,1≤r≤n列出各个S(n, r)的植如下
| r n | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | ||||
| 2 | 1 | 1 | |||
| 3 | 1 | 3 | 1 | ||
| 4 | 1 | 7 | 6 | 1 | |
| 5 | 1 | 15 | 25 | 10 | 1 |
定理 第二类Stirling数满足下面的递推关系
S(n, r)=r·S(n-1, r)+S(n-1, r-1) (n>1, r≥1)
证明:设n个不同的球为b1, b2, …, bn,从中取一个球设为b1。把这n个球放入r个盒子无一空盒的方案全体可分为两类:
(1)b1独占一盒,其余n-1个球放入r-1个盒子无一空盒的方案数为S(n-1,r-1)
(2)b1不独占一盒,这相当于先将b2, b3, …, bn。这n-1个球放入r个盒子,不允许有空盒的方案数共有S(n-1, r),然后将b1放入其中一盒,这一盒子有r种可挑选,故b1不独占一盒的方案数为r·S(n-1, r)。
根据加法原理,则有:
S(n, r)=r·S(n-1, r)+S(n-1, r-1)(n>1,r≥1)
对于n=r,或r=1,显然有S(n, n)=1,S(n, 1)=1。
综上所述,本题的算法可用第二类Stirling数的递推关系先求出S(n, r),再乘上r!,即得所求方案数。
主要算法描述如下:
(1)数据结构
const maxn=10 {球的最大数目}
var s:array[0..maxn, 0..maxn]of longint; {存放第二类数}
(2)用下列二重循环求S(n, r)
① 置S[0, 0]=1;
② for i:=1 to n do
for j:=1 to r do
S(i, j)=i*S(i-1,j)+S(i-1, j-1)
③ 计算方案数S
S:=S[n, r]
For i:=1 to r do S:=S*I;
9.4 取数游戏
| 源程序名 cycle.???(pas, c, cpp) 可执行文件名 cycle.exe 输入文件名 cycle.in 输出文件名 cycle.out |
【问题描述】
有一个取数的游戏。初始时,给出一个环,环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后,将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏,两人轮流取数,取数的规则如下:
(1)选择硬币左边或者右边的一条边,并且边上的数非0;
(2)将这条边上的数减至任意一个非负整数(至少要有所减小);
(3)将硬币移至边的另一端。
如果轮到一个玩家走,这时硬币左右两边的边上的数值都是0,那么这个玩家就输了。
如下图,描述的是Alice和Bob两人的对弈过程,其中黑色节点表示硬币所在节点。结果图(d)中,轮到Bob走时,硬币两边的边上都是0,所以Alcie获胜。
![]()
正在上传…重新上传取消
(a)Alice (b)Bob (c)Alice (d)Bob
现在,你的任务就是根据给出的环、边上的数值以及起点(硬币所在位置),判断先走方是否有必胜的策略。
【输入】
第一行一个整数N(N≤20),表示环上的节点数。
第二行N个数,数值不超过30,依次表示N条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。
【输出】
仅一行。若存在必胜策略,则输出“YES”,否则输出“NO”。
【样例】
cycle.in cycle.out
4 YES
2 5 3 0
cycle.in cycle.out
3 NO
0 0 0
【问题分析】
本题的数据规模(N≤20,边上的数值不超过30)实际上是一个幌子,是想误导我们走向搜索的道路。
考虑一个简化的问题。如果硬币的一边的数值为0,那么惟一可能取胜的走法就是向另一边移动,并且把边上的数减到0。因为如果不把边上的数减到0,那么下一步对方会将硬币移动到原来的位置,并且将边上的数减到0,这样硬币两边的数值就都为0了。所以,对于一边有0的情况,双方惟一的走法就是不停的向另一边移动,并取完边上的数值。因此,判断是否有必胜策略,就是看另一个方向上连续的非零边是否为奇数条。
那么两边都非零的情况呢?如果有一个方向上连续的非零边为奇数条,那么显然是有必胜策略的,因为只需往这个方向走并取完边上的数即可。如果两个方向上连续的非零边都是偶数条,则没有必胜策略。因为不管往哪个方向走,必然不能取完边上的数,否则必败。如果不取完,则下一步对方可以将硬币移动回原来的位置并取完边上的数,这样就变成了一边为0、另一边有偶数条连续的非零边的情况,还是必败。所以,对于一般的情况,只需判断硬币的两边是否至少有一边存在奇数条连续的非零边。如果存在,则有必胜策略;否则无必胜策略。算法的时间复杂度为O(N)。
9.5 磁盘碎片整理
| 源程序名 defrag.???(pas, c, cpp) 可执行文件名 defrag.exe 输入文件名 defrag.in 输出文件名 defrag.out |
【问题描述】
出于最高安全性考虑,司令部采用了特殊的安全操作系统,该系统采用一个特殊的文件系统。在这个文件系统中所有磁盘空间都被分成了相同尺寸的N块,用整数1到N标识。每个文件占用磁盘上任意区域的一块或多块存储区,未被文件占用的存储块被认为是可是用的。如果文件存储在磁盘上自然连续的存储块中,则能被以最快的速度读出。
因为磁盘是匀速转动的,所以存取上面不同的存储块需要的时间也不同。读取磁盘开头处的存储块比读取磁盘尾处的存储块快。根据以上现象,我们事先将文件按其存取频率的大小用整数1到K标识。按文件在磁盘上的最佳存储方法,1号文件将占用1, 2, …, S1的存储块,2号文件将占用S1+1, S1+2, …, S1+S2的存储块,以此类推(Si是被第i个文件占用的存储块的个数)。为了将文件以最佳形式存储在磁盘上,需要执行存储块移动操作。一个存储块移动操作包括从磁盘上读取一个被占用的存储块至内存并将它写入其他空的存储块,然后宣称前一个存储块被释放,后一个存储块被占用。
本程序的目的是通过执行最少次数的存储块移动操作,将文件安最佳方式存储到磁盘上,注意同一个文件的存储块在移动之后其相对次序不可改变。
【输入】
每个磁盘说明的第一行包含两个用空格隔开的整数N和K(1≤K≤N≤100000),接下来的K行每行说明一个文件,对第i个文件的说明是这样的:首先以整数Si开头,表示第i个文件的存储块数量,1<=Si<=N-K,然后跟Si个整数,每个整数之间用空格隔开,表示该文件按自然顺序在磁盘上占用的存储块的标识。所有这些数都介于1和N之间,包括1和N。一个磁盘说明中所有存储块的标识都是不同的,并且该盘至少有一个空的存储块。
【输出】
对于每一个磁盘说明,只需输出一行句子“We need M move operations”,M表示将文件按最佳方式存储到磁盘上所需进行的最少存储块移动操作次数。如果文件已按最佳方式存储,仅需输出“No optimization needed.”。
【样例】
defrag.in defrag.out
20 3 We need 9move operations
4 2 3 11 12
1 7
3 18 5 10
【问题分析】
本题可以看作是一个置换的调整问题。按文件块的目标位置对文件块编号后,调整文件块位置的问题就转化为调整置换的问题了。不过,本题还有一点特殊之处,就是存在一些数,它们不要求归位,这些数可作为交换空间。
找出所有的循环节,分情况讨论。如果一个循环节上所有的数都是要求归位的,那么必须先利用交换空间将一个数先交换出去,然后其他数都归位,最后再把交换出去的数换回来。如果这个循环节上有不需要归位的数,则可直接贪心,将可以归位的尽量归位即可。
9.6 欧几里德的游戏
| 源程序名 game.???(pas, c, cpp) 可执行文件名 game.exe 输入文件名 game.in 输出文件名 game.out |
【问题描述】
欧几里德的两个后代Stan和Ollie正在玩一种数字游戏,这个游戏是他们的祖先欧几里德发明的。给定两个正整数M和N,从Stan开始,从其中较大的一个数,减去较小的数的正整数倍,当然,得到的数不能小于0。然后是Ollie,对刚才得到的数,和M,N中较小的那个数,再进行同样的操作……直到一个人得到了0,他就取得了胜利。下面是他们用(25,7)两个数游戏的过程:
Start:25 7
Stan:11 7
Ollie:4 7
Stan:4 3
Ollie:1 3
Stan:1 0
Stan赢得了游戏的胜利。
现在,假设他们完美地操作,谁会取得胜利呢?
【输入】
第一行为测试数据的组数C。下面有C行,每行为一组数据,包含两个正整数M, N。(M, N不超过长整型。)
【输出】
对每组输入数据输出一行,如果Stan胜利,则输出“Stan wins”;否则输出“Ollie wins”
【样例】
game.in game.out
2 Stan wins
25 7 Ollie wins
24 15
【问题分析】
这是一道博弈题。解题的关键在于把握胜负状态的关系。
任意的状态只有两种可能:一种可能是胜状态——即有必胜策略,另一种可能是负状态——即没有必胜策略。对于任意的胜状态,无论如何走,都不可能走到另一个胜状态;而任意的负状态,至少存在一种走法可以走到胜状态。(0, 0)是初始的胜状态。
考察任意的状态(a, b),不妨假设a≥b。如果
![]()
正在上传…重新上传取消<2,则只有一种走法,即将(a, b)变为(a-b, b)。那么,(a, b)是何种状态就取决于(a-b, b)是何种状态:根据前面胜负状态的定义可知,(a-b, b)为胜状态时,(a, b)为负状态;(a-b, b)为负状态时,(a, b)为胜状态。
如果
![]()
正在上传…重新上传取消≥2,则至少存在两种走法:将(a, b)变为(c, b)或(c+b, b),这里c=a mod b。如果这两个状态中至少有一个是负状态,则根据定义(a, b)是胜状态。如果两个状态都是胜状态,由于(c+b, b)可以变为(c, b),这就与“胜状态只能走到负状态”产生了矛盾,所以两个状态都是胜状态的情况是不存在的。因此,≥2时,(a, b)必为胜状态。
总结一下前面的结论,设f(a, b)为状态(a, b)的胜负情况(1表示胜状态,0表示负状态),a≥b,则:
1、
![]()
正在上传…重新上传取消 2、
9.7 百事世界杯之旅
| 源程序名 pepsl.???(pas, c, cpp) 可执行文件名 pepsl.exe 输入文件名 pepsl.in 输出文件名 pepsl.out |
【问题描述】
“……在2002年6月之前购买的百事任何饮料的瓶盖上都会有一个百事球星的名字。只要凑齐所有百事球星的名字,就可参加百事世界杯之旅的抽奖活动,获得球星背包,随声听,更克赴日韩观看世界杯。还不赶快行动!”
你关上电视,心想:假设有n个不同的球星名字,每个名字出现的概率相同,平均需要买几瓶饮料才能凑齐所有的名字呢?
【输入】
整数n(2≤n≤33),表示不同球星名字的个数。
【输出】
输出凑齐所有的名字平均需要买的饮料瓶数。如果是一个整数,则直接输出,否则应该直接按照分数格式输出,例如五又二十分之三应该输出为:
3
5--
20
第一行是分数部分的分子,第二行首先是整数部分,然后是由减号组成的分数线,第三行是分母。减号的个数应等于分母的为数。分子和分母的首位都与第一个减号对齐。
分数必须是不可约的。
【样例】
pepsi.in pepsi.out
2 3
【提示】
“平均”的定义:如果在任意多次随机实验中,需要购买k1, k2, k3, …瓶饮料才能凑齐,而k1, k2, k3, …出现的频率分别是p1, p2, p3, …,那么,平均需要购买的饮料瓶数应为:k1* p1+k2*p2+k3* p3+…
【算法分析】
这道题目主要考察的是数学的推导能力。假设f[n, k]为一共有n个球星,现在还剩k个未收集到,还需购买饮料的平均次数。则有:
![]()
正在上传…重新上传取消
经移项整理,可得:
![]()
正在上传…重新上传取消
我们所要求的实际上应该是f(n, n),根据f(n, k)的递推式,可得
![]()
正在上传…重新上传取消
其中,H(n)表示Harmonic Number。
9.8 倒酒
| 源程序名 pour.???(pas, c, cpp) 可执行文件名 pour.exe 输入文件名 pour.in 输出文件名 pour.out |
【问题描述】
Winy是一家酒吧的老板,他的酒吧提供两种体积的啤酒,a ml和b ml,分别使用容积为a ml和b ml的酒杯来装载。
酒吧的生意并不好。Winy发现酒鬼们都非常穷。有时,他们会因为负担不起aml或者bml啤酒的消费,而不得不离去。因此,Winy决定出售第三种体积的啤酒(较小体积的啤酒)。
Winy只有两种杯子,容积分别为a ml和b ml,而且啤酒杯是没有刻度的。他只能通过两种杯子和酒桶间的互相倾倒来得到新的体积的酒。
为了简化倒酒的步骤,Winy规定:
(1)a≥b;
(2)酒桶容积无限大,酒桶中酒的体积也是无限大(但远小于桶的容积);
(3)只包含三种可能的倒酒操作:
①将酒桶中的酒倒入容积为b ml的酒杯中;
②将容积为a ml的酒杯中的酒倒入酒桶;
③将容积为b ml的酒杯中的酒倒入容积为a ml的酒杯中。
(4)每次倒酒必须把杯子倒满或把被倾倒的杯子倒空。
Winy希望通过若干次倾倒得到容积为a ml酒杯中剩下的酒的体积尽可能小,他请求你帮助他设计倾倒的方案
【输入】
两个整数a和b(0<b≤a≤109)
【输出】
第一行一个整数c,表示可以得到的酒的最小体积。
第二行两个整数Pa和Pb(中间用一个空格分隔),分别表示从体积为a ml的酒杯中倒出酒的次数和将酒倒入体积为b ml的酒杯中的次数。
若有多种可能的Pa、Pb满足要求,那么请输出Pa最小的一个。若在Pa最小的情况下,有多个Pb满足要求,请输出Pb最小的一个。
【样例】
pour.in pour.out
5 3 1
1 2
倾倒的方案为:
1、桶->B杯; 2、B杯->A杯;
3、桶->B杯; 4、B杯->A杯;
5、A杯->桶; 6、B杯->A杯;
【问题分析】
解模方程。
首先,c=gcd(a, b)。写成模方程形式即为bx≡c(mod a)。
设Pa,Pb分别为从体积为a ml。的酒杯中倒出酒的次数和将酒倒入体积为b mL的酒杯
中的次数,则有c=bPb-aPa。
用Euclid辗转相除法求出Pa,Pb即可。时间复杂度为O(log2n)。
9.9 班级聚会
| 源程序名 reunion.???(pas, c, cpp) 可执行文件名 reunion.exe 输入文件名 reunion.in 输出文件名 reunion.out |
【问题描述】
毕业25年以后,我们的主人公开始准备同学聚会。打了无数电话后他终于搞到了所有同学的地址。他们有些人仍在本城市,但大多数人分散在其他的城市。不过,他发现一个巧合,所有地址都恰好分散在一条铁路线上。他准备出发邀请但无法决定应该在哪个地方举行宴会。最后他决定选择一个地点,使大家旅行的花费和最小。
不幸的是,我们的主人公既不擅长数学,也不擅长计算机。他请你帮忙写一个程序,根据他同学的地址,选择聚会的最佳地点。
【输入】
输入文件的每一行描述了一个城市的信息。
首先是城市里同学的个数,紧跟着是这个城市到Moscow(起点站)的距离(km),最后是城市的名称。最后一行描述的总是Moscow,它在铁路线的一端,距离为0。
【输出】
聚会地点城市名称和旅行费用(单程),两者之间用一空格隔开。每km花费一个卢布。
【样例】
reunion.in reunion.out
7 9289 Vladivostok Yalutorovsk 112125
5 8523 Chabarovsk
3 5184 Irkutsk
8 2213 Yalutorovsk
10 0 Moscow
【问题分析】
中位数问题。找这样一个点(城市)——它左边的人数与右边的人数差的绝对值最小。时间复杂度为O(n)。
本问题的参考程序作者特意不加注释,以考察读者能否根据以上问题分析,将程序看懂并理解。