文章目录
- 前言
- 一、今天学习了什么?
- 二、动态规划
- 1.概念
- 2.题目
- 总结
前言
提示:这里为每天自己的学习内容心情总结;
Learn By Doing,Now or Never,Writing is organized thinking.
提示:以下是本篇文章正文内容
一、今天学习了什么?
- 学习了代码随想录关于动态规划的算法;
- 还有01背包问题
二、动态规划
1.概念
「动态规划」(Dynamic Programming),适用于很多重叠子问题的场景**,每一个结果一定是由于上一个状态推导出来的,选择和状态转移**。解题步骤如下:
- 确定dp数组(dp table)以及下标的含义;
- 确定递推公式;
- dp数组如何初始化;
- 确定遍历顺序;
- 举例推导dp数组;
「01 背包问题」是指,有 n 个物品和一个最多能背负 w 重量的背包,求该背包能背负的最大重量。第 i 个物品的重量为 weight[i] ,价值为 value[i] 。
有两种解法:
- 二维数组:
- dp[i] [j] ,表示从下标为 [0,i] 的物品中,放进背包容量为 j 时的最大价值;
- 确定遍历的顺序,先遍历背包容量,再去逐个遍历物品个数;
- 一维数组:
- dp[i] ,表示背包容量为 i 时的背包最大价值;
- 先遍历物品,再去遍历背包容量,并且保证遍历背包容量时是从大到小的,保证物品只会被放入了一次。
/**
* - 采用二维数组解决背包问题
* - 只有当当前背包的容量能放下当前物品的重量时,才需要去判断是否需要将物品放入背包中
* - 按照先遍历物品,再去遍历背包容量的顺序执行
*/
public static int testWeightBagProblem01(int[] weight, int[] value, int bagSize) {
int m = weight.length;
int[][] dp = new int[m][bagSize + 1];
for (int j = weight[0]; j <= bagSize; j++) {
dp[0][j] = value[0];
}
for (int j = 1; j <= bagSize; j++) {
for (int i = 1; i < m; i++) {
if (j >= weight[i]) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[m - 1][bagSize];
}
/**
* - 一维数组
* - 背包容量的最大值取决于之前背包容量更小时候的最大值
*/
public static int testWeightBagProblem02(int[] weight, int[] value, int bagSize) {
int[] dp = new int[bagSize + 1];
for (int i = 0; i < weight.length; i++) {// 先遍历物品
for (int j = bagSize; j >= weight[i]; j--) {// 再去遍历背包容量
// 判断将此物品放入背包的结果
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); //不放、放
}
}
return dp[bagSize];
}
2.题目
- 509. 斐波那契数
public int fib(int n) {
if (n == 0 || n == 1) {
return n;
}
/**
* 动态规划
* - dp数组
* - 选择
* - 状态转移
* dp[i] 代表f(n)
*/
int[] dp = new int[n + 3];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
- 70. 爬楼梯
public int climbStairs(int n) {
if (n == 1 || n == 2) {
return n;
}
/**
* 遇到重叠子问题,采用动态规划
* - dp数组含义:dp[i]表示有dp[i]种方法可以爬到楼顶(楼顶的台阶数为i)
* - 初始化
* - 状态转移和选择
*/
int[] dp = new int[n + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
- 746. 使用最小花费爬楼梯
public int minCostClimbingStairs(int[] cost) {
/**
* - 采用动态规划
* - dp[i]:爬上i层使用的最少的花费
*/
int[] dp = new int[cost.length + 1];
for (int i = 2; i <= cost.length; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.length];
}
- 62. 不同路径
public int uniquePaths(int m, int n) {
/**
* - 每次都需要选择,采用动态规划
* - dp[i][j]:到达(i,j)点的路径
*/
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
- 63. 不同路径 II
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
/**
* 还是使用动态规划,只不过需要判断是否可达
*/
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
if (obstacleGrid[i][0] == 1) {
break;
}
dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {
if (obstacleGrid[0][j] == 1) {
break;
}
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) {
continue;
}
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
- 343. 整数拆分
public int integerBreak(int n) {
if (n <= 3) {
return n - 1;
}
/**
* - 如何使用动态规划呢?
* - 就需要从怎么拆入手
* - 是否要拆,取决于拆完后结果和之前的结果谁更大
*/
int[] dp = new int[n + 1];
dp[2] = 1;
for (int i = 3; i <= n; i++) {
for (int j = 1; j <= i - j; j++) {
dp[i] = Math.max(dp[i], Math.max((i - j) * j, dp[i - j] * j));
}
}
return dp[n];
}
public int integerBreak2(int n) {
if (n <= 3) {
return n - 1;
}
/**
* - 这是纯数学解答
* - 任何整数都可以拆成2和3
* - 怎么拆,取决于模上3的余数是多少
*/
int remainder = n % 3;
int times = n / 3;
if (remainder == 0) {
return (int) Math.pow(3, times);
} else if (remainder == 1) {
return (int) Math.pow(3, times - 1) * 4;
} else {
return (int) Math.pow(3, times) * 2;
}
}
- 96. 不同的二叉搜索树(⭐⭐⭐⭐⭐)
这个题有点难,在于如何的合适区拆分成子问题:
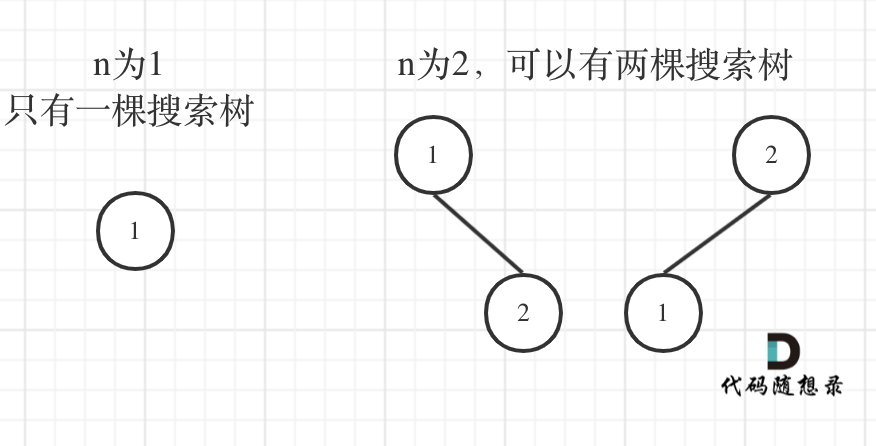
应该先举几个例子,画画图,看看有没有什么规律,如图:
- 当
n = 1 , 2时都很直观; - 当
n = 3时,分为:- 当1为头结点的时候,其右子树有两个节点,看这两个节点的布局,是不是和 n 为2的时候两棵树的布局是一样的啊!
- 当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
- 当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
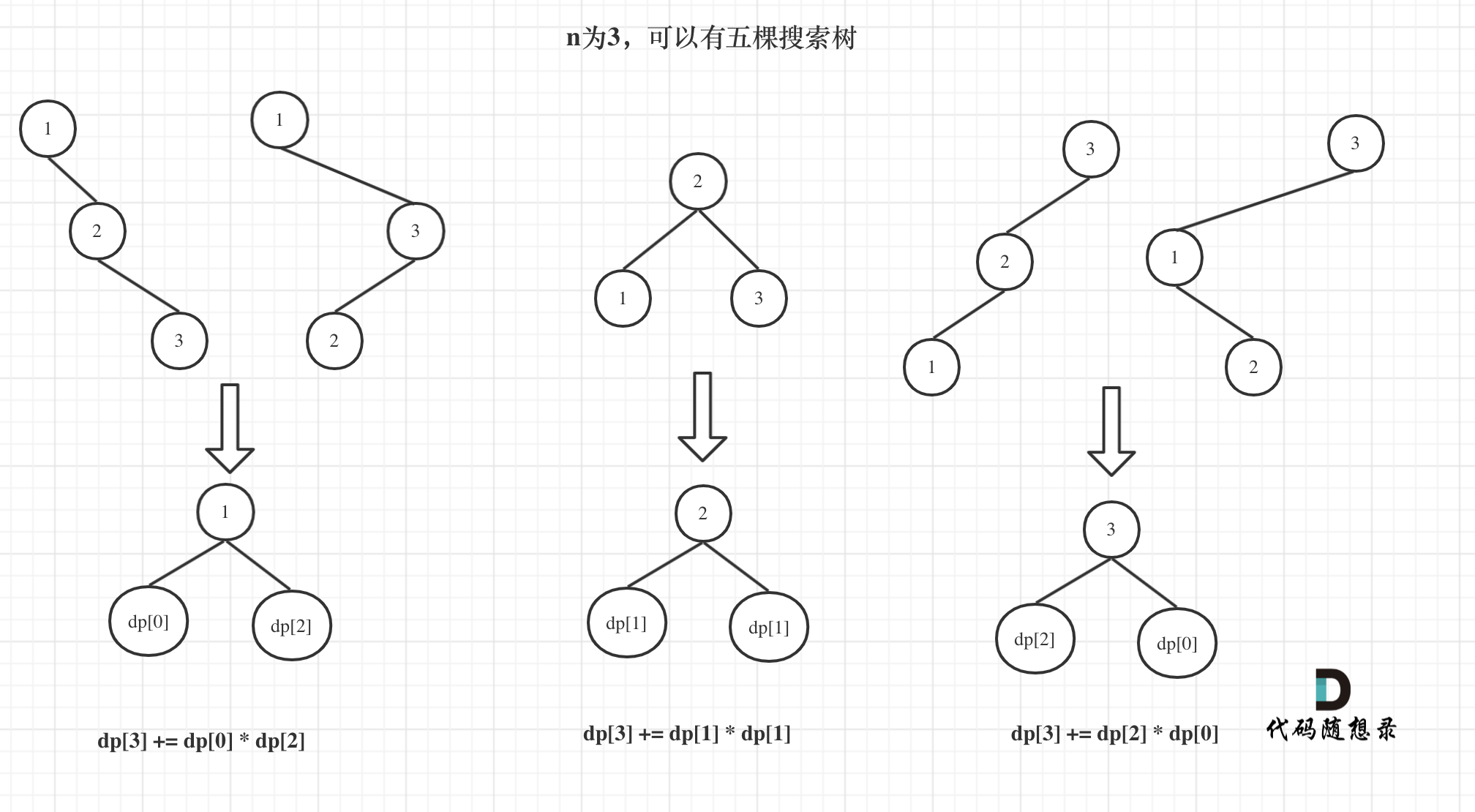
- dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量;
- dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2];
- 元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量;
- 元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量;
- 元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量;
public int numTrees(int n) {
/**
* - 这个题有点难,在于如何正确的处理拆分子问题
* - dp[i],代表i个节点组成的二叉搜索树的种数
* - 拆分为 1.2.3.....i 为头节点组成的二叉搜索树的之和就是i个节点组成的二叉搜索树的种数
*/
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[i - j] * dp[j - 1];
}
}
return dp[n];
}
- 416. 分割等和子集(⭐⭐⭐)
public boolean canPartition(int[] nums) {
/**
* - 可以将问题看成,是否能将数组中的元素凑出数组元素和的一半
* - 背包容量为一半的数组和,物品价值和物品重量都是nums数组
* - 采用一维数组的话,dp[i]代表数组容量为i时能背的最大价值
*/
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if (sum % 2 != 0) {
return false;
}
sum /= 2;
int[] dp = new int[sum + 1];
for (int i = nums[0]; i <= sum; i++) {
dp[i] = nums[0];
}
for (int i = 1; i < nums.length; i++) {
for (int j = sum; j >= nums[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
return dp[sum] == sum;
}
- 1049. 最后一块石头的重量 II
public int lastStoneWeightII(int[] stones) {
/**
* - 也是背包问题
*/
int sum = 0;
for (int i = 0; i < stones.length; i++) {
sum += stones[i];
}
int target = sum / 2;
int[] dp = new int[target + 1];
for (int i = stones[0]; i <= target; i++) {
dp[i] = stones[0];
}
for (int i = 1; i < stones.length; i++) {
for (int j = target; j >= stones[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - 2 * dp[target];
}
总结
提示:这里对文章进行总结:
今天效率一般,心情有点emo,很害怕。