力扣刷题笔记（每日更新~）

提示：这里可以添加本文要记录的大概内容：

本文主要用于记录刷题笔记，温故而知新~

提示：以下是本篇文章正文内容，下面案例可供参考

一、什么是时间复杂度？

时间复杂度： 时间复杂度是衡量算法运行时间随输入规模增长而增长的速度。它表示算法执行所需的基本操作次数或步骤数量。通常使用大O记号（O）来表示时间复杂度，表示最坏情况下的运行时间上界。常见的时间复杂度包括：

O(1)：常数时间复杂度，算法的执行时间与输入规模无关。
O(log n)：对数时间复杂度，常见于二分查找等分治算法。
O(n)：线性时间复杂度，算法的执行时间与输入规模成正比。
O(n logn)：线性对数时间复杂度，常见于快速排序、归并排序等排序算法。
O(n^2)：平方时间复杂度，常见于冒泡排序、插入排序等。
O(2^n)：指数时间复杂度，通常表示暴力枚举等指数级别的算法。

空间复杂度： 空间复杂度是衡量算法所需的内存空间随输入规模增长而增长的速度。与时间复杂度类似，它也表示算法的额外资源消耗。通常也使用大O记号来表示空间复杂度。常见的空间复杂度包括：

O(1)：常数空间复杂度，算法的内存使用与输入规模无关，只使用有限的固定额外内存。
O(n)：线性空间复杂度，算法的内存使用与输入规模成正比。
O(n^2)：平方空间复杂度，通常表示算法使用了二维数组等随着输入规模平方级别增长的内存。

二、什么是递归？

递归是一种编程技术，其中一个函数在其定义中调用自己，以解决问题或执行任务。递归可用于解决可以被分解为更小的相似子问题的问题。

举个套娃的例子来说明递归：

在这里插入图片描述

假设有一组套娃，每个套娃都可以包含另一个更小的套娃。我们的任务是逐个打开套娃，直到所有的套娃都被打开。这可以通过递归来实现。

 1. 打开最外层的套娃
 2. 在最外层套娃中找到下一层的套娃
 3. 重复步骤 2，直到找到最内层的套娃
 4. 逐层返回，打开每个套娃

递归的特点（方法的反复调用）：

一个问题的解可以分为几个子问题的解
问题和子问题的求解思路完全一样，除了数据规模不同
存在终止条件

三、刷题记录

leetcode 70-爬楼梯

力扣题库地址：爬楼梯
题目：
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
示例1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

分析图片：
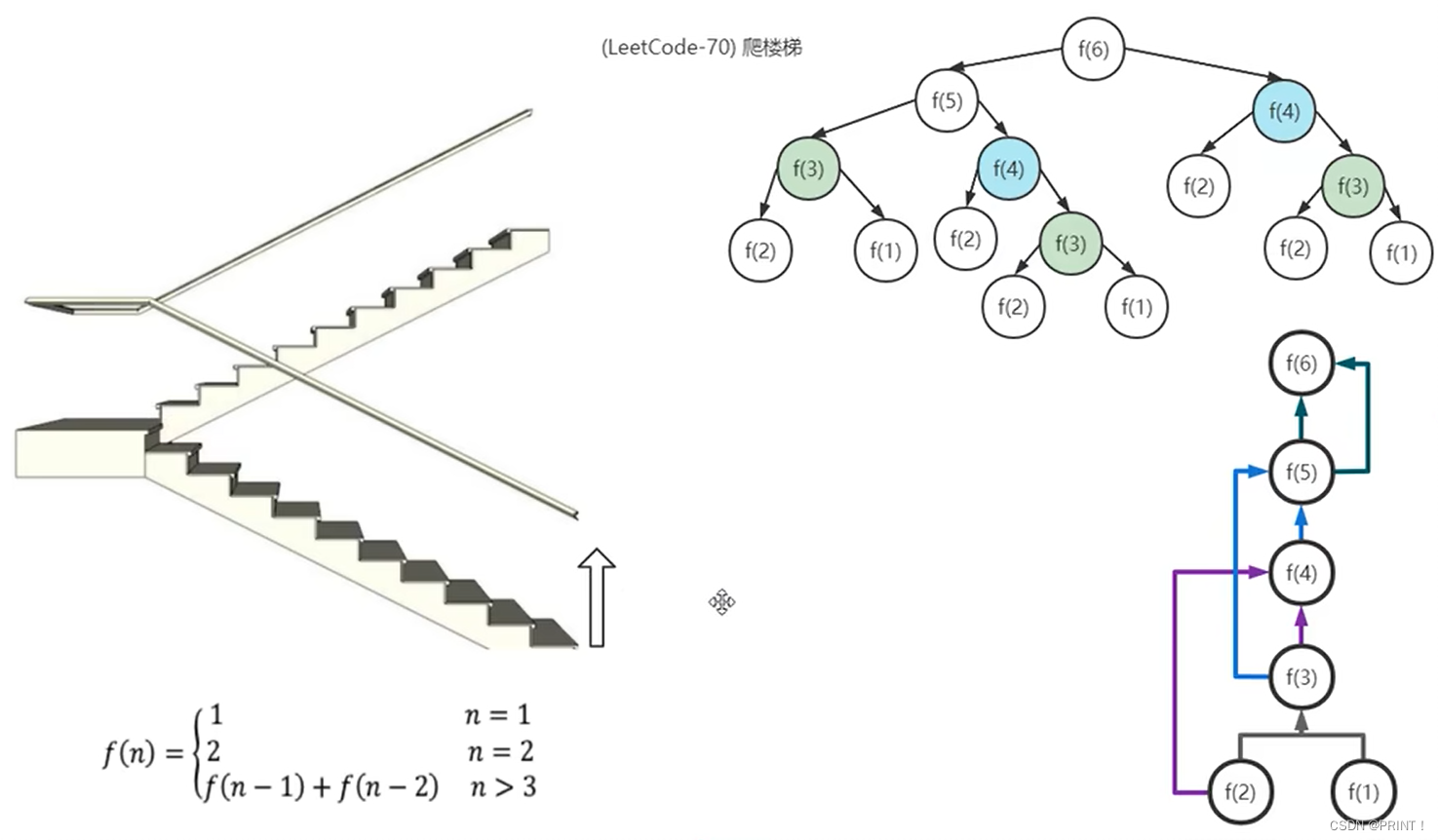
在这里插入图片描述
执行代码：

public class StudyDemo {
    public static void main(String[] args){
        int n = 20;
        System.out.println(method(n));
    }

    public static int method(int n){
        if(n==1){
            return 1;
        } else if (n==2) {
            return 2;
        }else {
            int pre = 2;
            int prePre = 1;
            int result = 0;
            for(int i=3;i<=n;i++){
                result = pre+prePre;
                prePre = pre;
                pre = result;
            }
            return result;
        }
    }
}