题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

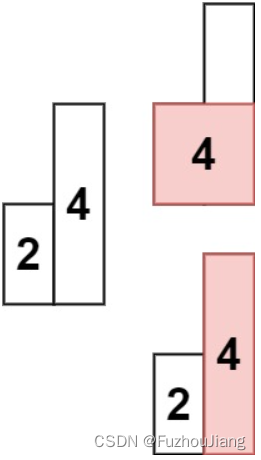
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

解答

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
#if 0   // 双指针法
        vector<int> minLeftIndex(heights.size());
        vector<int> minRightIndex(heights.size());
        int size = heights.size();

        // 记录每个柱子左边第一个小于该柱子的下标
        minLeftIndex[0] = -1;
        for(int i = 1; i < size; i++)
        {
            int t = i - 1;
            // 不断向左寻找
            while(t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
            minLeftIndex[i] = t;
        }

        // 记录每个柱子右边第一个小于该柱子的下标
        minRightIndex[size - 1] = size;
        for(int i = size - 2; i >= 0; i--)
        {
            int t = i + 1;
            // 不断向左寻找
            while(t < size && heights[t] >= heights[i]) t = minRightIndex[t];
            minRightIndex[i] = t;
        }

        int res = 0;
        for(int i = 0; i < size; i++)
        {
            int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
            res = max(sum, res);
        }
        return res;
#else   // 单调栈，栈顶到栈底要从大到小，遇到比栈顶小的元素即计算可能结果
        // 栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求的最大面积的高度和宽度（低高低！！！）
        int res = 0;
        stack<int> st;

        // 数组头尾补上0
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        st.push(0);

        for(int i = 1; i < heights.size(); i++)
        {
            if(heights[i] > heights[st.top()])
            {
                st.push(i);
            }
            else if(heights[i] == heights[st.top()])
            {
                st.pop();
                st.push(i);
            }
            else
            {
                // 低高（栈顶元素）低（当前元素） 构成可能答案
                while(!st.empty() && heights[i] < heights[st.top()])
                {
                    int mid = st.top();
                    st.pop();
                    if(!st.empty())
                    {
                        int left = st.top();
                        int right = i;
                        int w = right - left - 1;
                        int h = heights[mid];
                        res = max(res, w * h);
                    }
                }
            }
            st.push(i);
        }
        return res;
#endif

    }
};