Array ColoringArray Coloring
题目大意
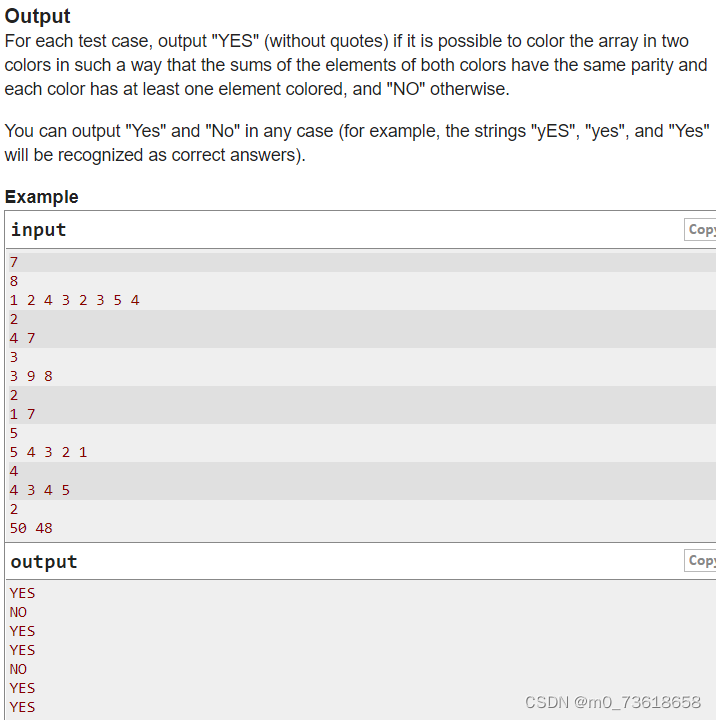
题目要求判断是否可以将数组元素分为两种颜色,使得两种颜色元素的和具有相同的奇偶性,并且每种颜色至少有一个元素被着色。
思路分析
可以通过统计数组中奇数和偶数的个数来判断是否满足条件。分析可知,如果奇数的个数是偶数个,则一定可以满足条件。
时间复杂度
O(n)
AC代码
#include<bits/stdc++.h>
using namespace std;
void solve()
{
int n;
cin>>n;
vector<int> a(n);
int od=0,ev=0;
for(int i=0;i<n;i++){
cin>>a[i];
if(a[i]%2) od++;
else ev++;
}
if(od%2==0)
cout<<"Yes\n";
else cout<<"No\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int t;
cin>>t;
while(t--)
solve();
return 0;
}
B. Maximum RoundingB. Maximum Rounding
题目大意
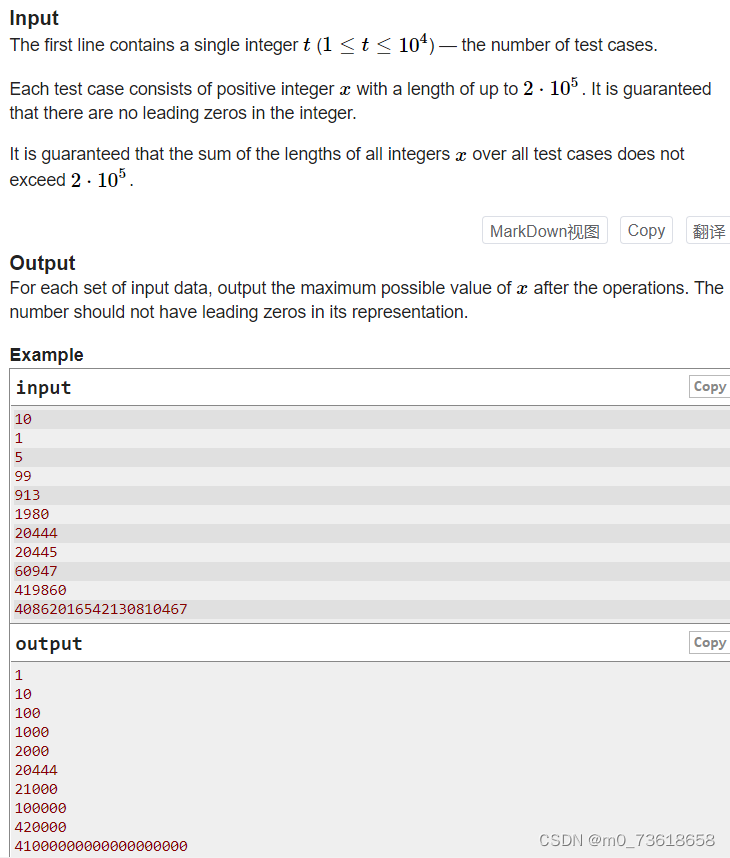
题目要求对给定的数字进行操作,使其尽可能地大。操作规则如下:
选择一个正整数 k,并将数字 x 向第 k 位取整。
注意:位数从右往左编号,从0开始。如果数字有 k 位,则认为第 k 位上的数字为0。
取整操作如下:
如果第 (k-1) 位上的数字大于等于 5,则将第 k 位上的数字加1;否则第 k位上的数字保持不变(采用数学取整规则)。
如果操作前第 k 位上的数字为9,并且需要增加1,则需要找到一个最小的位置 k’(k’>k),使得第 k’ 位上的数字小于9,并将第 k’ 位上的数字加1。然后令 k=k’。
之后,将小于 k 的所有位替换为0。
思路分析
从右往左遍历数字,如果当前位上的数字大于等于5,则将上一位的数字加1;如果当前位上的数字为9,并且需要增加1,则向左找到一个最小的位置可以进行加1操作。最后将小于当前位的所有位替换为0。这样可以确保得到最大的数字。
时间复杂度
O(n)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
string s;
cin>>s;
int p=-1;
for(int i=s.size()-1;i>0;i--)
if(s[i]>='5'){
s[i-1]++;
p=i;
}
if(s[0]>='5') cout<<'1',p=0; // 如果第一位大于等于5,直接输出1
for(int i=p;i<s.size();i++)
s[i]='0';
cout<<s<<endl;
}
return 0;
}
C. Assembly via MinimumsC. Assembly via Minimums
题目大意
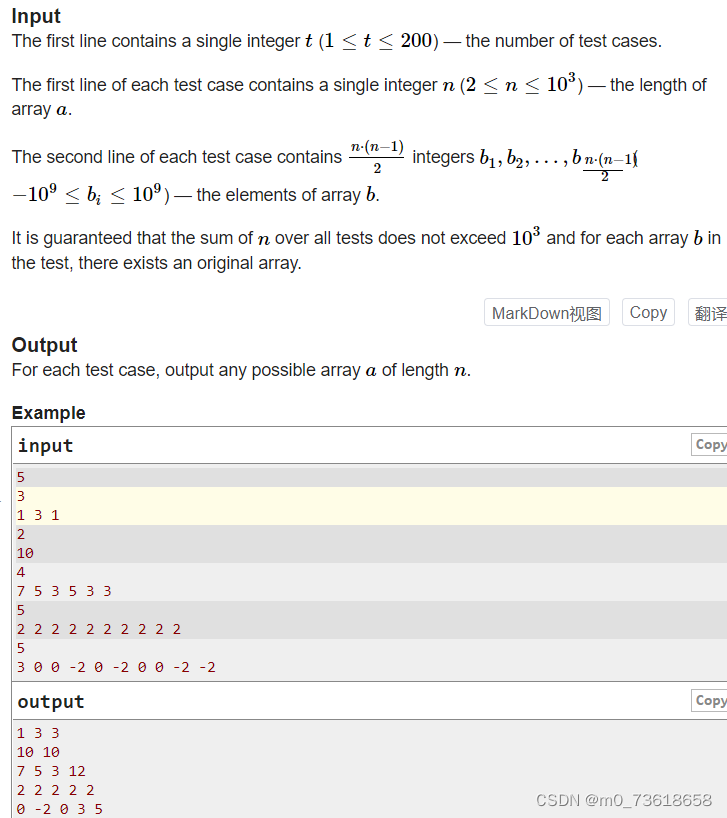
Sasha有一个整数数组a,他对于所有的i和j (i<j),都写下了ai和aj的最小值,从而得到了一个新的数组b。然后他随机地打乱了数组b的元素。不幸的是,他忘记了原来的数组a,你的任务是从数组b恢复出可能的数组a。
思路分析
本题与顺序无关,a组排好序从小到大对应b组(n-1)个a[0],(n-2)个a[1],(n-3)个a[2],…
例如:b 3 3 3 5 5 7
a 3 5 7 100000
最小的a[0]在b中有n-1=4-1=3个,因为以a[0]为最小的数对有n-1个,所以在b中a有n-1个
最后一个a[i]是最大值,必须大于b中的最大值(这样b中的最大值才能成为一个数对的更小的那个),只要是数列a的最大值即可
时间复杂度
O(n2 log n)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int t;cin>>t;
while(t--)
{
int n;cin>>n;
int m=n*(n-1)/2,b[m];
for(int i=0;i<m;i++)cin>>b[i];
sort(b,b+m); // 对数组b进行排序
for(int i=0;i<m;i+=--n)cout<<b[i]<<' '; //i每次加上--n,最小的的b[0]有n-1个......
cout<<"1000000000\n";
}
}
D. Strong VerticesD. Strong Vertices
题目大意
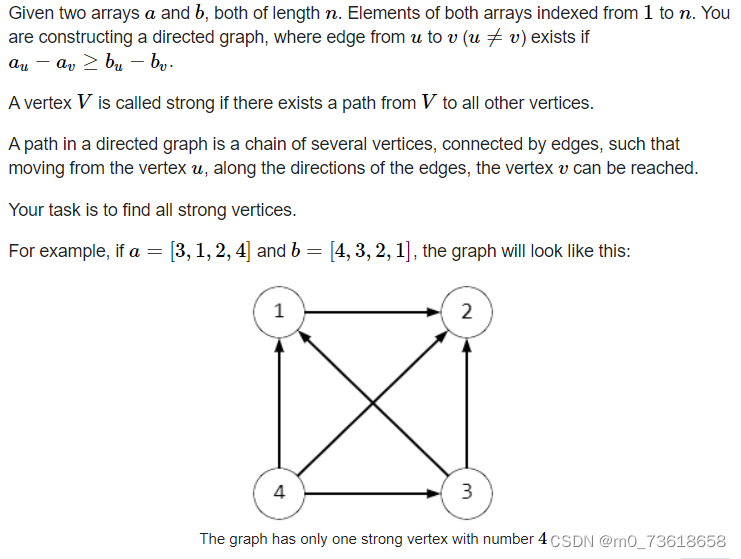
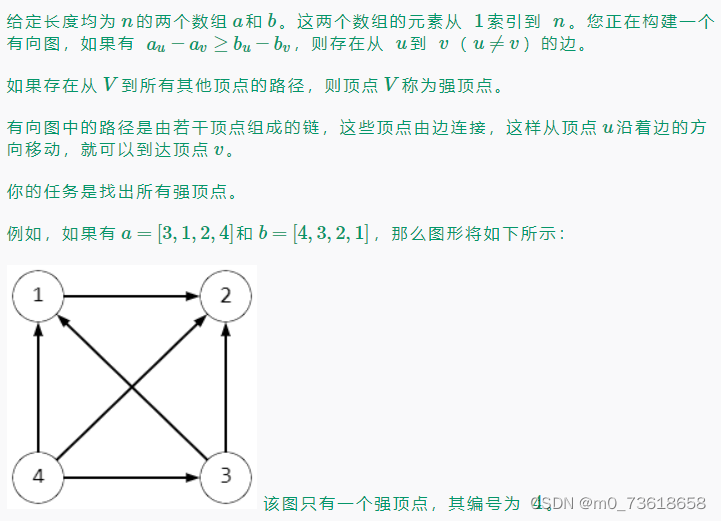
要求找出所有的strong vertices。给定两个长度为n的数组a和b,我们需要构建一个有向图,如果对于任意的u≠v,满足au−av≥bu−bv,则存在一条从u到v的边。
思路分析(摘自官方题解)
首先将不等式变形为au−bu≥av−bv。然后我们可以定义一个新数组c,其中ci=ai−bi,这样不等式变成了cu≥cv。
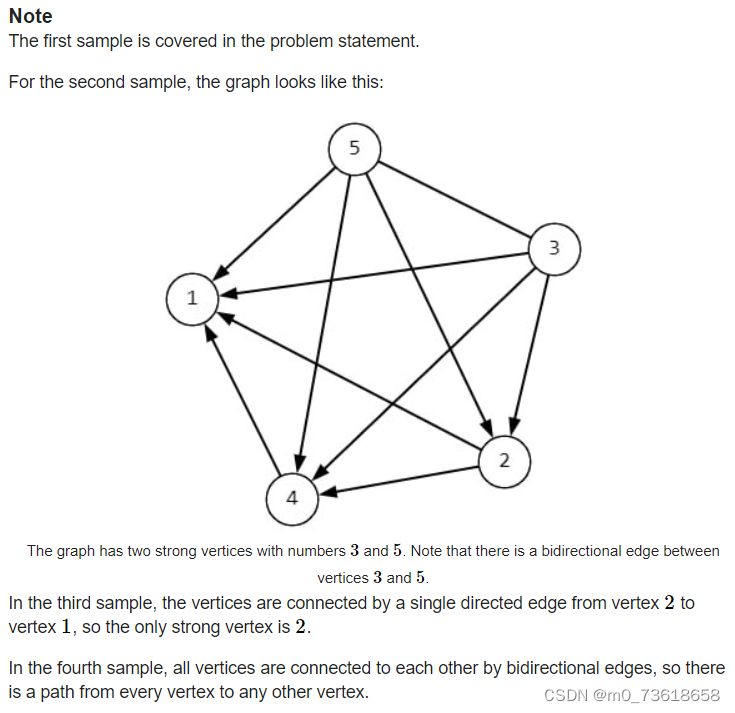
假设集合p1,…pm是具有最大cv的顶点v的集合。从每个pi都有一条到其他所有顶点的路径,因为cpi不小于任何其他的cu值,所以集合p一定在我们的答案中。
接下来的问题是是否还有其他顶点在我们的答案中?
我们来证明一下,对于任意不是最大值的顶点v,那么v到p中的任何顶点都没有路径。首先观察到v和任何pi之间没有边。所以路径必须经过其他顶点。但是即使存在到另一个顶点u的路径,cu仍然小于cpi,所以无法到达任何pi。
因此,我们可以得出结论,答案将始终是使cv最大化的顶点集合。
时间复杂度
O(t*n)
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int a[N],b[N];
int main()
{
int t;cin>>t;
while(t--)
{
int n;cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)cin>>b[i];
int mx=INT_MIN;
for(int i=1;i<=n;i++)mx=max(mx,a[i]-b[i]);
int c=0;
for(int i=1;i<=n;i++)c+=(a[i]-b[i]==mx);
cout<<c<<"\n";
for(int i=1;i<=n;i++)if(a]-b[i]==mx)cout<<i<<' ';
cout<<"\n";
}
}
E. Power of PointsE. Power of Points
题目大意
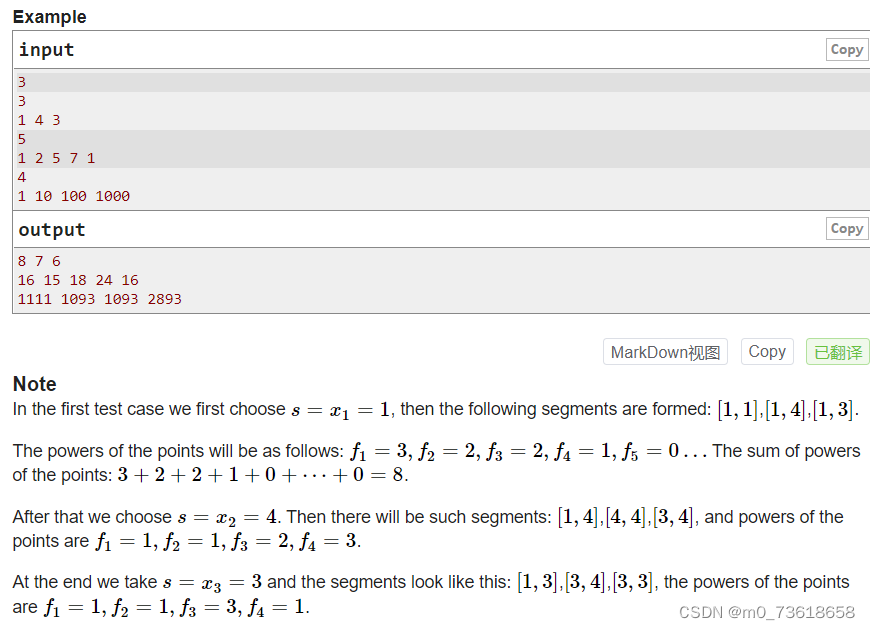
给定一个包含n个点的数轴,每个点具有整数坐标。对于每个整数s,我们构造线段将s与每个点连接起来,然后计算每个整数点在这些线段中的交点数。
思路分析
首先对给定的点进行排序。然后,用两个变量s1和s2分别记录当前已遍历的点的坐标和和剩余点的坐标和。遍历每个点,更新s1和s2的值,并计算该点的幂。最后输出所有点的幂。
官方题解

时间复杂度
O(nlogn)
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
pair<int,int>x[N];
long long a[N];
int main()
{
int t;cin>>t;
while(t--)
{
int n;cin>>n;
long long s1=0,s2=0;
for(int i=1;i<=n;i++)
{
cin>>x[i].first;
x[i].second=i;
s2+=x[i].first;
}
sort(x+1,x+n+1);
for(int i=1;i<=n;i++)
{
s2-=x[i].first;
s1+=x[i].first;
a[x[i].second]=n+1ll*x[i].first*(2*i-n)-s1+s2;
}
for(int i=1;i<=n;i++)cout<<a[i]<<" \n"[i==n];
}
}
F. Sum and Product
题目大意
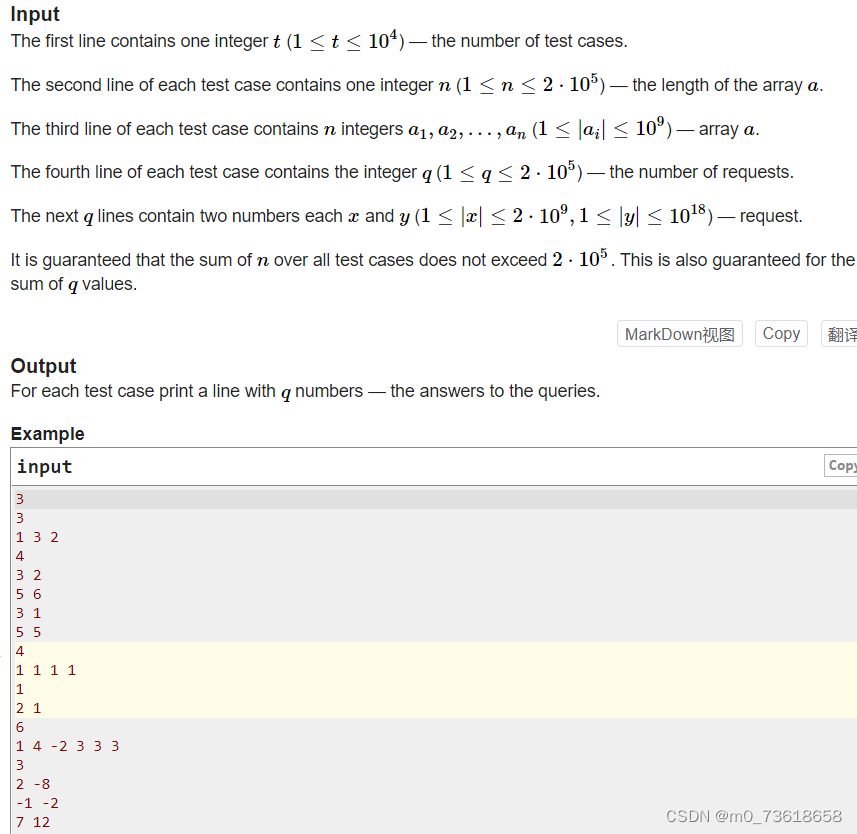
给定一个长度为n的数组a,以及q个查询。每个查询给定两个数x和y,要求找出满足以下条件的数组元素对(i,j)的数量:1≤i<j≤n、ai+aj=x,以及ai⋅aj=y。
思路分析
这个问题可以通过使用哈希映射和二分查找来解决。首先将数组a中的所有元素放入哈希映射中,然后对于每个查询,计算出满足条件的i和j对的数量。
-
首先,将数组a中的所有元素放入哈希映射中。
-
然后,对于每个查询,计算出满足ai+aj=x和aiaj=y的i和j对的数量。
-
最后,我们输出满足条件的i和j对的数量。
官方题解

时间复杂度
O(n+q)
AC代码
#include<bits/stdc++.h>
using namespace std;
map<long long,int>cnt;
long long my_sqrt(long long a)
{
long long l=0,r=5000000001;
while(r-l>1)
{
long long mid=(l+r)/2;
if(1ll*mid*mid<=a)l=mid;
else r=mid;
}
return l;
}
long long get(int b,long long c)
{
long long D=1ll*b*b-4ll*c;
if(D<0)return 0;
long long x1=(b-my_sqrt(D))/2;
long long x2=(b+my_sqrt(D))/2;
if(x1+x2!=b||x1*x2!=c)return 0;
if(x1==x2)return 1ll*cnt[x1]*(cnt[x1]-1)/2ll;
else return 1ll*cnt[x1]*cnt[x2];
}
int main()
{
int t;cin>>t;
while(t--)
{
int n;cin>>n;
cnt.clear();
for(int i=1;i<=n;i++)
{
int x;cin>>x;
cnt[x]++;
}
int q;cin>>q;
for(int i=0;i<q;i++)
{
int b;long long c;
cin>>b>>c;
cout<<get(b,c)<<" \n"[i==q-1];
}
}
}
G. Counting GraphsG. Counting Graphs
题目大意
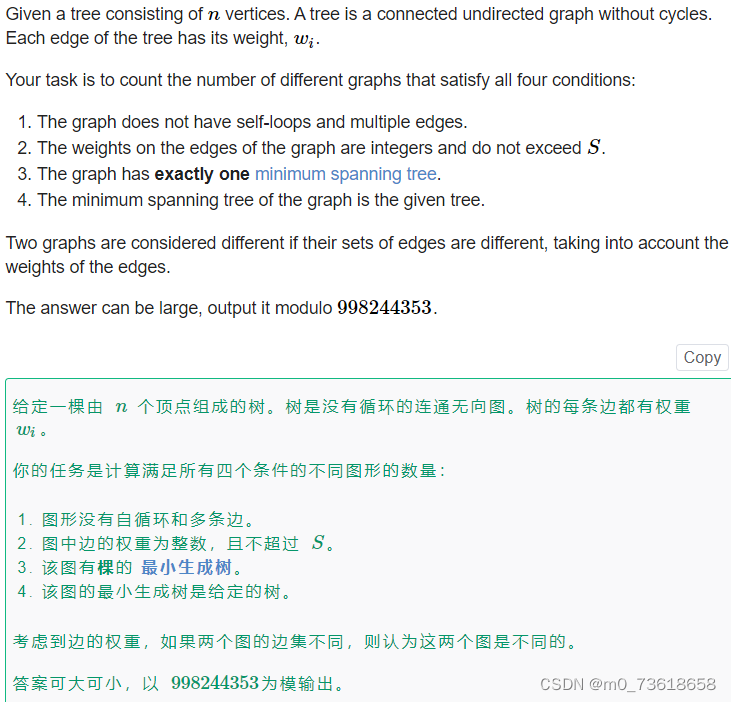
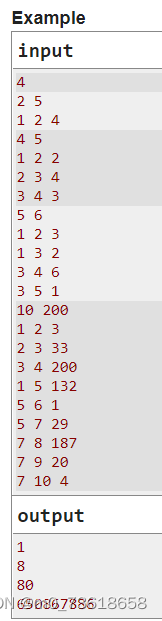
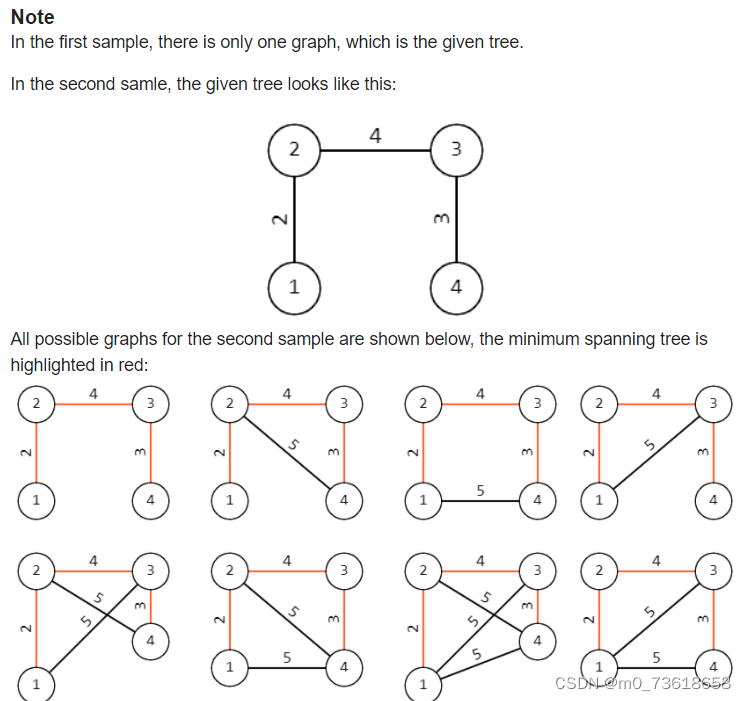
要求计算满足一定条件的不同图形的数量。给定一棵由n个顶点组成的树,树的每条边都有一个权重wi。需要找出满足以下条件的不同图形的数量:
1.图形没有自循环和多条边。
2.图中边的权重为整数,且不超过S。
3.该图有一棵最小生成树。
4.该图的最小生成树是给定的树。
思路分析
可以使用Kruskal算法来构建最小生成树,并计算满足条件的图形的数量。
- 首先,读取整数t,表示有t个测试用例。对于每个测试用例,读取整数n和S,分别表示树的顶点数和权重的上限。接下来,使用一个for循环读取每个边的信息,并将边按照权重从小到大进行排序。
- 然后,初始化并查集p和sz,并将每个顶点初始化为一个独立的连通分量。使用另一个for循环遍历每条边,将当前边的两个顶点所在的连通分量合并,并计算满足条件的图形的数量。
- 在合并连通分量的过程中,可以使用并查集来快速查找每个顶点所属的连通分量的领导节点。同时,还需要维护每个连通分量的大小sz。
- 为了计算满足条件的图形的数量,可以使用幂运算binpow来求解。对于每条边a[i],假设当前边连接的两个连通分量的大小分别为sub_u和sub_v,那么符合条件的图形的数量为(S-a[i].w+1)^(sub_u*sub_v-1),将这个结果乘到ans上。
- 最后,输出ans即为满足条件的不同图形的数量。
官方题解

时间复杂度
O(nlogn)
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N = 200000, mod = 998244353;
int p[N + 1], sz[N + 1];
struct edge
{
int u, v, w;
void read() { cin >> u >> v >> w; } // 读取边的信息
bool operator<(edge x) { return w < x.w; } // 按照边的权重进行排序
} a[N + 1];
int leader(int v)
{
if (p[v] == v)
return v;
else
return p[v] = leader(p[v]);
}
void unite(int u, int v)
{
u = leader(u);
v = leader(v);
p[u] = v; // 合并两个连通分量
sz[v] += sz[u]; // 更新连通分量的大小
}
long long binpow(long long a, long long n)
{
if (n == 0)
return 1;
if (n % 2 == 0)
return binpow(a * a % mod, n / 2);
else
return a * binpow(a, n - 1) % mod; // 幂运算
}
int main()
{
int t;
cin >> t;
while (t--)
{
int n, S;
cin >> n >> S;
for (int i = 1; i <= n; i++)
p[i] = i, sz[i] = 1; // 初始化并查集和连通分量大小
for (int i = 0; i < n - 1; i++)
a[i].read(); // 读取边的信息
sort(a, a + n - 1); // 按照权重排序
long long ans = 1;
for (int i = 0; i < n - 1; i++)
{
int sub_u = sz[leader(a[i].u)];
int sub_v = sz[leader(a[i].v)];
ans = ans * binpow(S - a[i].w + 1, 1ll * sub_u * sub_v - 1) % mod; // 计算满足条件的图形的数量
unite(a[i].u, a[i].v); // 合并连通分量
}
cout << ans << "\n";
}
return 0;
}