文章目录
- 前言
- 问题
- 状态向量和观测向量
- 加性噪声的形式
- 状态方程及求导
- 观测方程及求导
- 状态初始化
- 过程噪声和观测噪声
- 卡尔曼滤波过程
- code
前言
卡尔曼滤波器在1960年被卡尔曼发明之后,被广泛应用在动态系统预测。在自动驾驶、机器人、AR领域等应用广泛。卡尔曼滤波器使用类似马尔可夫链的性质,假设系统状态只与上一时刻的系统状态有关。基础的卡尔曼滤波器使用线型方程对系统状态进行建模。为了能够应用到非线性系统,扩展卡尔曼滤波器利用泰勒展开,并只保留一次项,抛弃高次项,将非线性关系近似为线性关系。
问题
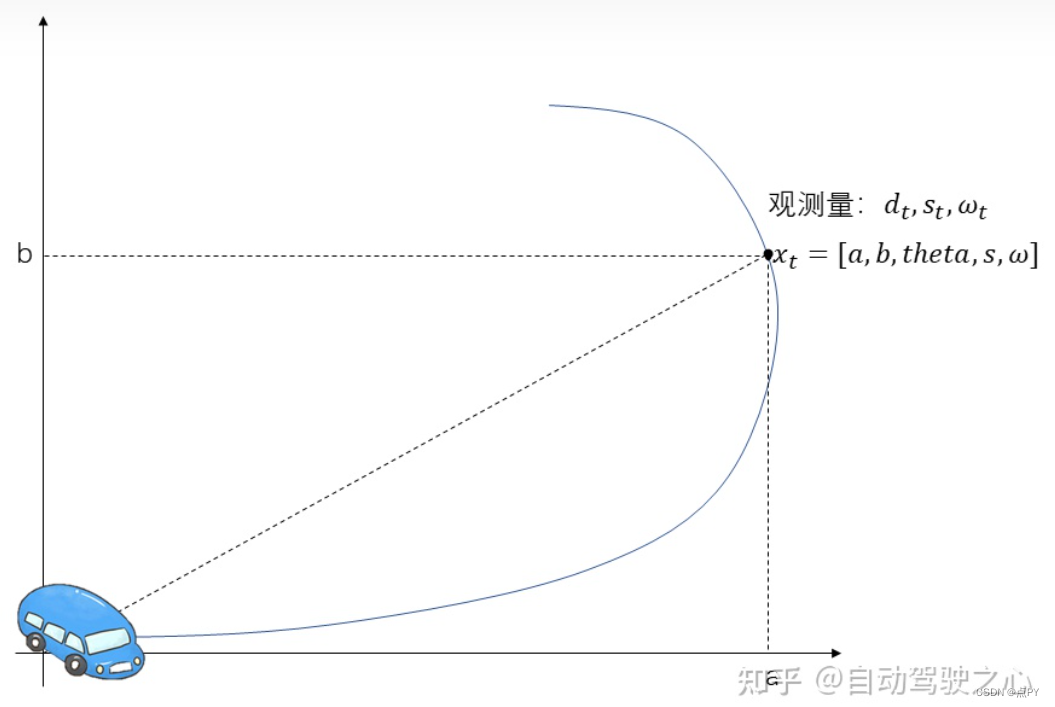
假设有一个小车从原点出发,每个时间间隔ΔT,车上的传感器可以输出车此时的速度ωt 和角速度ωt。同时,在原点处有一个探测器,同样可以每个ΔT的时间间隔,探测出车辆距离原点的距离dt。 我们希望能够求出小车每一时刻对应的x轴和y轴坐标at , bt
状态向量和观测向量
我们另小车每一时刻的x,y坐标、此时小车的车身角度,速度和角速度这5个状态当作状态向量,于是
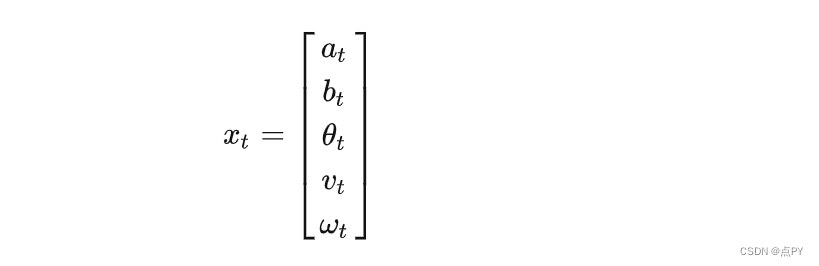
同时,另观测向量为距离原点距离的平方、速度、角速度,于是

加性噪声的形式
为了简化计算过程,我们这里将噪声项提到非线性方程外面,变成加性噪声的形式。
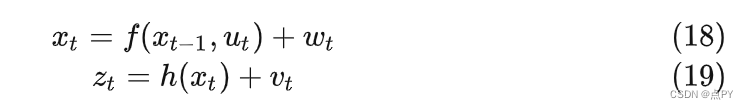
状态方程及求导
小车的x坐标等于上一时刻的x坐标以及这个时间段小车行使过的距离在x轴的投影。小车在每个时间段形式的距离为
v*ΔT;距离在x轴的投影相当于乘上cos(θ)。y坐标同理。角度则是每一时刻的角速度积分。于是,我们可以写出状态方程: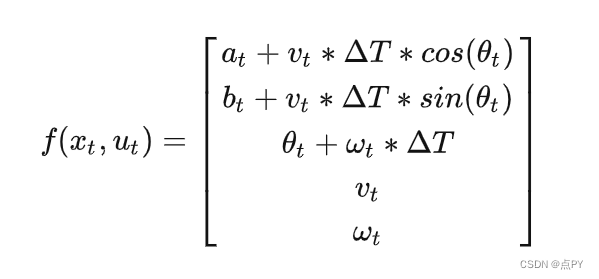
将函数f相对于状态向量xt求偏导数,可以得到
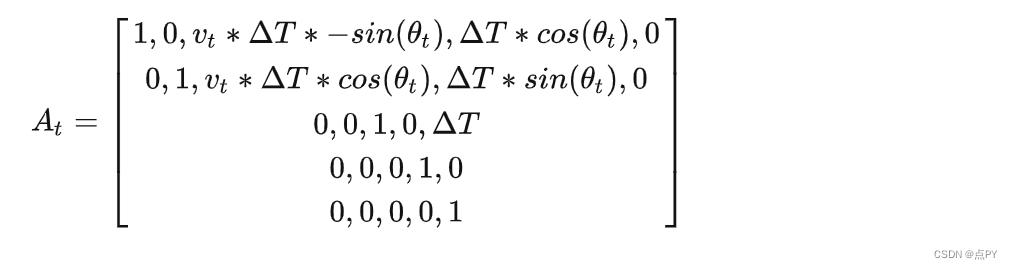
观测方程及求导
我们将小车与原点距离的平方、速度、角速度作为观测向量,即
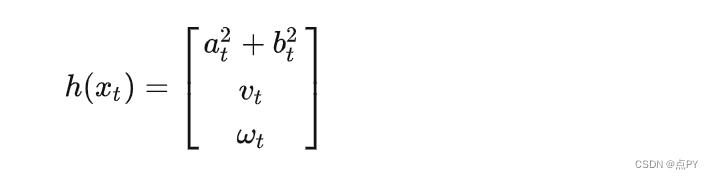
将上述方程对状态方程求偏导数可以得到
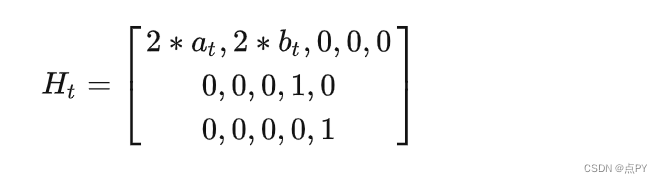
状态初始化
系统状态我们可以简单以全0向量作为初始值,即

另一个需要初始化的值是状态向量协方差矩阵P0。经过实验发现在滤波过程对P0的值似乎有点敏感,主要是不能只有对角线有值。实际上,如果在实际应用中,可以先采集一段数据计算出各个变量的初始值。这里将P0设为如下值

过程噪声和观测噪声
过程噪声的协方差和观测噪声的协方差矩阵我们设置为一个较小的值即可。只不过这里的Q矩阵似乎比较敏感。而且由于我们用了速度和角速度做积分,而另外一个观测量距离并不能为角度提供更多的信息。因此,对于角度,这里并不能得到比简单的积分好很多的结果。
# 过程噪声的协方差,需要调整的参数
Q = np.array([
[0.01, 0, 0, 0, 0],
[0, 0.01, 0, 0, 0],
[0, 0, 0.0001, 0, 0],
[0, 0, 0, 0.01, 0],
[0, 0, 0, 0, 0.01]
])
# 观测噪声协方差矩阵
R = np.array([
[0.0001, 0, 0],
[0., 0.0001, 0],
[0, 0, 0.0001]
]) # 观测噪声的协方差,需要调整的参数
卡尔曼滤波过程
有了上面的雅各比矩阵推导,就可以利用公式(13-17)进行滤波过程。过程只用了到一些矩阵乘法,十分简单。具体可以看代码。

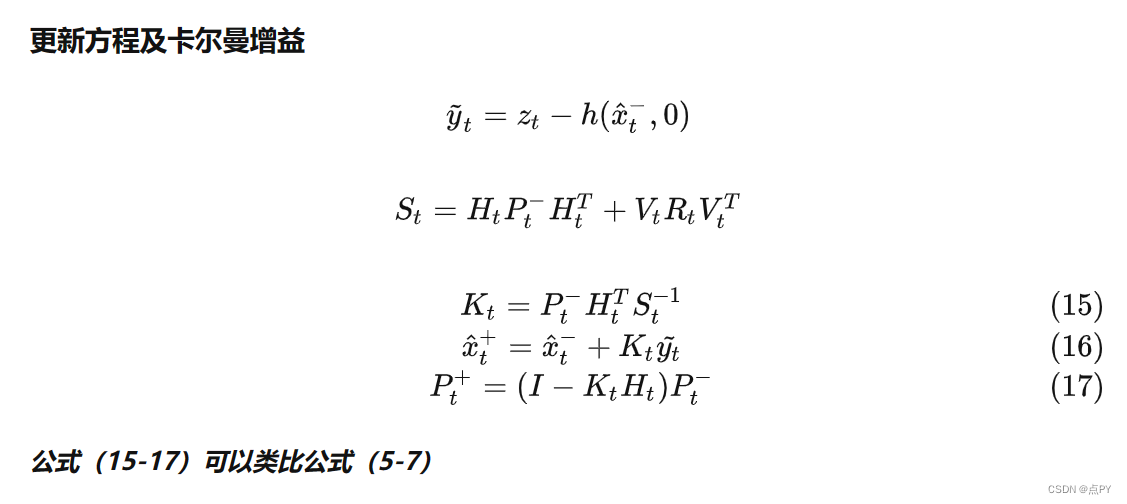
code
https://github.com/zeal-up/KalmanFilterTutorial