行列式意义是什么?
行列式等于它的各个列对应的向量张成的平行2n面体的体积,这是因为行列式是一个交替多重线性形式,而我们通常理解的欧式空间中的体积也是这样一个函数(单位立方体体积为1,沿某条边扩大c倍体积就扩大c倍,交换两条边以后体积反号——这一条是补充定义的,我们认为体积是有向体积,其数值表示体积大小,正负号表示各条边的排列顺序或坐标轴手性),而满足归一性、多线性、反对称性的函数是唯一的,所以行列式的直观理解就是欧式空间中的有向体积。
用矩阵与线性变换的同构来解释也很好理解,行列式就是矩阵对应的线性变换对空间的拉伸程度的度量,或者说物体经过变换前后的体积比。特别地,如果矩阵不是满秩的,意味着一个nnn维的空间变换后被压扁了,变成了其中的一个n−1n-1n-1维的超平面甚至是维度更低的超直线,所以原来空间中的体积元在变换后体积为0,此时行列式也是0。多元函数积分作变量代换后要乘一个Jacobi行列式就是这个道理,表示变换前后的微元体积比。
=
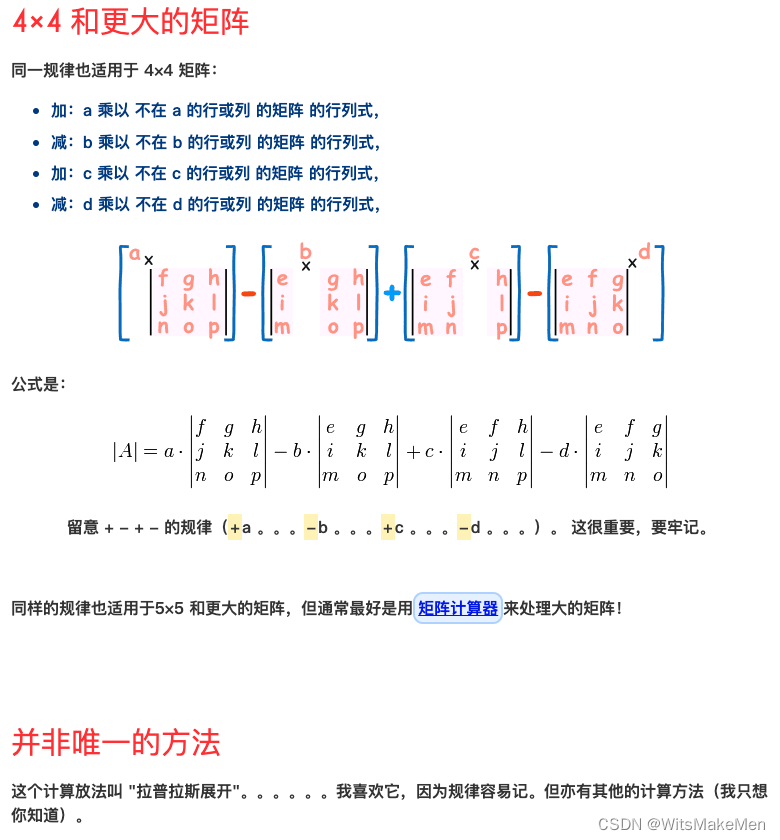
矩阵的行列式