NLP学习笔记(一) RNN基本介绍

news2025/1/19 22:04:50

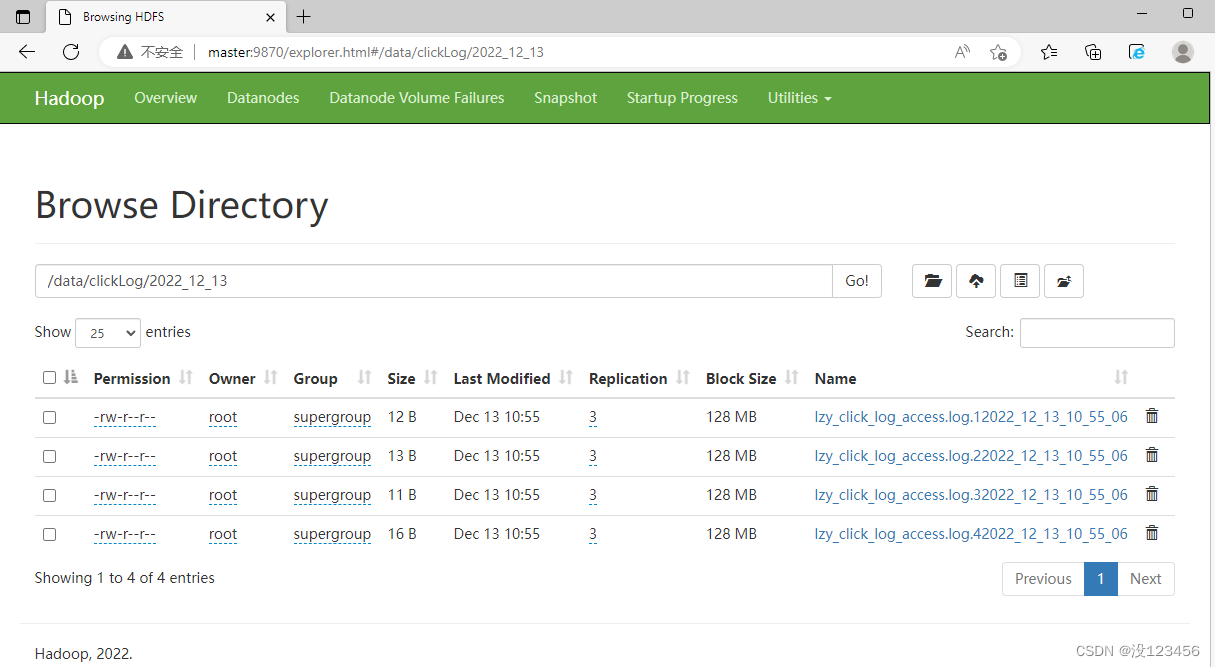
大家好，我是半虹，这篇文章来讲循环神经网络 (Recurrent Neural Network, RNN)

文章行文思路如下：

首先通过前馈神经网络引出为啥需要循环神经网络
然后介绍循环神经网络的核心思想与运作方式
最后拓展两个循环神经网络常见且常用的变体

在讲循环神经网络前，先来回顾下前馈神经网络，这是深度学习中最基础的网络结构之一

前馈神经网络也称为多层感知机，由多个隐藏层叠加得到，每个隐藏层可看作是一个线性模型加激活函数

为简单起见，这里先以单层感知机为例进行介绍

上图是单层感知机的结构示意图，其中， $X$ 是输入， $H$ 是输出

对应的公式表达如下所示：
$\alpha(X W_{xh} + b_{h})$
其中， $W_{xh}$ 和 $b_{h}$ 都是隐藏层的参数，表示可学习的权重矩阵， $\alpha$ 是激活函数

研究表明，前馈神经网络具有很强的学习能力，只要有足够多训练数据，理论上能拟合任意函数

既然如此，那为什么还需要有循环神经网络呢

这是因为前馈神经网络只能单独处理每个输入，对于网络而言，前一个输入和后一个输入是没有任何关系的

这在处理时序数据时前馈神经网络就会显得力不从心，一个典型的场景就是文本处理

举个例子，假设现在我们需要完成一个词性标注任务，给定的句子是：我在看画

如果用前馈神经网络完成上述任务时，就会出现下面的情况：

这是因为前馈神经网络对于句子中的每个词都是独立处理的

对于画这个词，在不给定上下文的情况下，它既可以是动词，也可以是名词，这时候网络无法判断它的词性

而人是怎么判断词性的呢？当我们发现看是动词时，自然就能推断画是名词，因为动词后接的是名词

这就引出一个重要的结论，在处理文本时，网络需要根据之前的词语来理解当前的词语

这就是循环神经网络的核心，在处理序列当前的数据时，同时考虑序列之前的数据

循环神经网络是怎么做到这一点的呢？答案就是：使用一个隐状态保存之前的信息，具体网络结构请看下图：

要注意这里的隐状态跟隐藏层不是一回事噢

上图左半部分是循环神经网络的结构示意图，右半部分是其按时间展开的示意图

可以看到，循环神经网络当前隐藏层的输出不仅取决于当前的输入，而且取决于先前隐藏层的输出

对应的公式表达如下所示：
$H_{t} = \alpha(X_{t} W_{xh} + H_{t-1} W_{hh} + b_{h})$
其中， $H_{t}$ 是当前隐藏层， $X_{t}$ 是当前输入， $H_{t-1}$ 是先前隐藏层， $W_{xh}$ 、 $W_{hh}$ 和 $b_h$ 都是可学习的参数

对比循环神经网络和前馈神经网络的结构表示和公式表达，可以很清楚地发现两者的区别

在结构表示上，循环神经网络增加了一个隐状态，能保存上一个隐藏层的信息

在公式表达上，循环神经网络计算当前隐藏层时，不仅取决于当前输入，还会考虑先前的隐藏层

能理解这两点，就能理解循环神经网络的核心思想

为了帮助大家进一步理解循环神经网络的工作方式，下面我们举一个例子来说，并给出关键代码

假设我们用循环神经网络对下面这个句子进行编码：我在画画

import torch
import torch.nn as nn

# 定义输入数据
# 对于输入句子我在画画，首先用独热编码得到其向量表示

x1 = torch.tensor([1, 0, 0]).float() # 我
x2 = torch.tensor([0, 1, 0]).float() # 在
x3 = torch.tensor([0, 0, 1]).float() # 画
x4 = torch.tensor([0, 0, 1]).float() # 画

h0 = torch.zeros(5) # 初始化隐状态

# 定义模型参数
# 模型的输入是三维向量，这里定义模型的输出是五维向量

W_xh = nn.Parameter(torch.randn(3, 5), requires_grad = True)
W_hh = nn.Parameter(torch.randn(5, 5), requires_grad = True)
b_h  = nn.Parameter(torch.randn(5)   , requires_grad = True)

# 前向传播

h1 = torch.tanh(torch.matmul(x1, W_xh) + torch.matmul(h0, W_hh) + b_h)
h2 = torch.tanh(torch.matmul(x2, W_xh) + torch.matmul(h1, W_hh) + b_h)
h3 = torch.tanh(torch.matmul(x3, W_xh) + torch.matmul(h2, W_hh) + b_h)
h4 = torch.tanh(torch.matmul(x4, W_xh) + torch.matmul(h3, W_hh) + b_h)

# 结果验证
# 可以发现，即使是对于同一个词语，得到的表示也是不一样的
# 这是因为在计算当前词语时，会考虑先前的词语

print(h3) # tensor([0.9787, 0.9974, 0.9995, 0.9999, 0.9970])
print(h4) # tensor([0.6867, 0.6352, 0.9994, 0.2269, 0.9801])