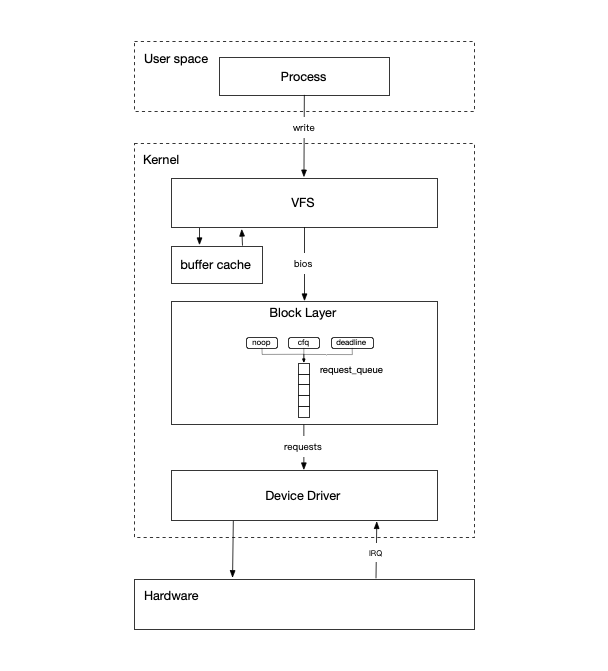
算法竞赛入门【码蹄集进阶塔335题】(MT2226-2250)
文章目录
- 算法竞赛入门【码蹄集进阶塔335题】(MT2226-2250)
- 前言
- 为什么突然想学算法了?
- 为什么选择码蹄集作为刷题软件?
- 目录
- 1. MT2226 36进制2
- 2. MT2227 36进制3
- 3. MT2228 36进制4
- 4. MT2229 excel的烦恼
- 5. MT2230 单条件和
- 6. MT2231 lowbit
- 7. MT2232 位运算
- 8. MT2233 三进制计算机1
- 9. MT2234 三进制计算机2
- 10. MT2235 整数大小比较
- 11. MT2236 升级版斐波那契数列
- 12. MT2237 2的n次幂
- 13. MT2238 大斐列
- 14. MT2239 个数统计
- 15. MT2240 个数统计2
- 16. MT2241 幸运数
- 17. MT2242 num++
- 18. MT2243 A+B problem
- 19. MT2244 A-B problem
- 20. MT2245 求圆周率
- 21. MT2246 派的n位
- 22. MT2247 进行一个幂的运算
- 23. MT2248 快速幂
- 24. MT2249 幂和
- 25. MT2250 Good Num的数量
- 结语
前言

为什么突然想学算法了?
> 用较为“官方”的语言讲,是因为算法对计算机科学的所有分支都非常重要。 在绝大多数的计算机科学分支领域中,要想完成任何实质性的工作,理解算法的基础知识并掌握与算法密切相关的数据结构知识是必不可少的。
> 但从实际而言,是因为当下快到了考研和找工作的年纪(ಥ_ಥ),无论走哪一条路,都不免需要一些相对丰富的算法知识,是故,便产生了一个暑假速成算法的计划,可能对于像我这种算法竞赛小白而言,几乎很难,但我仍然还是想尝试一下,毕竟,梦想还是要有的,万一实现了呢?~( ̄▽ ̄~)~

为什么选择码蹄集作为刷题软件?
码蹄集,是在全国高等学校计算机教学与产业实践资源建设专家委员会(TIPCC) 指导下建设的,其依托全国各大名校计算机系和清华大学出版社等单位的强大资源,旨在为计算机学习爱好者提供全面和权威的计算机习题。
目录
1. MT2226 36进制2
(1)题目描述
36进制,是数据的一种表示方法。同我们日常生活中的表示法不一样。它由0-9,A-Z组成。与10进制的对应关系是:O-9对应O-9;A-Z对应10-35。
本题中,请你创建一个36进制类,统一使用大写字母,使其能够进行== ,l=, > ,>=,<,<=比较。
格式
输入格式:
第一行输入一个整数n,表示比较次数。
接下来n行,每行输入一个比较操作,格式如下:
.
输出格式: 对于每个比较操作,输出比较的结果。
样例1
输入:
8
84 <= Q
J9VM < UETR
4H == 9M
-W4L >= IKL
-PP7 <= U9W
L7G != L7G
UII5X > TVCFW
A90H2 >= Z41Q1
.
输出:
False
True
False
False
True
False
True
False
备注:
保证:对于100%的数据: 1≤n ≤2,000,输入的36进制数不超过1,001位。
(2)参考代码
def main():
#code here
n = int(input())
for i in range(n):
x,op,y=input().split(" ")
x = int(x,36)
y = int(y,36)
if op == "==":
print(x==y)
elif op=="<=":
print(x<=y)
elif op==">=":
print(x>=y)
elif op=="<":
print(x<y)
elif op==">":
print(x>y)
elif op=="!=":
print(x!=y)
if __name__ == '__main__':
main();
2. MT2227 36进制3
(1)题目描述
36进制,是数据的一种表示方法。同我们日常生活中的表示法不一样。它由0-9,A-Z组成。与10进制的对应关系是:0-9对应O-9;A-Z对应10-35。
本题中,请你创建一个36进制类,我们要求其能进行加法与减法操作,统一使用大写字母。其中初始36进制数为0,请你输出进行了n次操作后这个数的36进制值。
格式
输入格式:
第一行输入一个十进制整数n,n表示操作组数。
接下来n行,每行输入一个36进制整数,若该数前面无符号,则为加法;若该数前面有个负号,则为减法。
.
输出格式:
输出进行了n项操作后,36进制数的值。
样例1
输入:
7
123
-ABC
456
0
-FZ
8FZ
QWERTY
.
输出: QWEUPV
备注:
保证:对于100%的数据:1<n ≤20,000,输入的36进制数不超过1,001位。
(2)参考代码
def base10_to_base36(num):
num_str = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
prefix = ""
if num == 0:
return "0"
base36 = []
if num < 0:
prefix = "-"
num = -num
while num != 0:
num, i = divmod(num, 36) # 返回 number // 36 , number%36
base36.append(num_str[i])
return prefix + "".join(reversed(base36))
def base36_to_base10(numStr):
if numStr.startswith("-"):
return -int(numStr.lstrip("-"), 36)
return int(numStr, 36)
def main():
n = int(input())
sum = 0
for i in range(n):
sum += base36_to_base10(input())
print(base10_to_base36(sum))
pass
if __name__ == '__main__':
main()
3. MT2228 36进制4
(1)题目描述
36进制,是数据的一种表示方法。同我们日常生活中的表示法不一样。它由0一9,A-Z组成。与10进制的对应关系是: 0-9对应0一9;A-Z对应10-35。
本题中,请你创建一个36进制类,我们要求其能进行乘法操作,统一使用大写字母。
格式
输入格式:
第一行输入一个整数n,表示数据组数。对于每组数据,输入两个36进制整数α和b。
.
输出格式: 输出一行一个36进制整数表示a与b的乘积。
样例1
输入:
6
0 -Z
1 1
10 10
-Z -Z
QWE RTY
-JK JK
.
输出:
0
1
100
Y1
KSNZV8
-AMF4
备注:
保证:对于100%的数据: 1n ≤40,输入的36进制数不超过1,001位。
(2)参考代码
def base10_to_base36(num):
num_str = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
prefix = ""
if num == 0:
return "0"
base36 = []
if num < 0:
prefix = "-"
num = -num
while num != 0:
num, i = divmod(num, 36) # 返回 number // 36 , number%36
base36.append(num_str[i])
return prefix + "".join(reversed(base36))
def base36_to_base10(numStr):
if numStr.startswith("-"):
return -int(numStr.lstrip("-"), 36)
return int(numStr, 36)
def main():
n = int(input())
for i in range(n):
x, y = [base36_to_base10(j) for j in input().split()]
print(base10_to_base36(x*y))
pass
if __name__ == '__main__':
main()
4. MT2229 excel的烦恼
(1)题目描述
你用过Excel嘛?
在excel中,第一列被标为A,第二列为B,以此类推,第26列为Z。接下来为由两个字母构成的列号:第27列为AA,第28列为AB…在标为ZZ的列之后则由三个字母构成列号,如此类推。
行号为从1开始的整数。
单元格的坐标由列号和行号连接而成。比如,BC23表示位于第55列23行的单元格。
有时也会采用被称为RXCY的坐标系统,其中X与Y为整数,坐标(X,Y)直接描述了对应单元格的位置。比如,R23C55即为前面所述的单元格。
您的任务是编写一个程序,将所给的单元格坐标转换为另一种坐标系统下面的形式。
格式
输入格式:
第一行一个整数T(1≤T<105)表示将有T次询问。
接下来T行,每行一个坐标。
输出T行,每行一个被转换的坐标。
.
输出格式: n行,每行一个被转换的坐标。
样例1:
输入:
3
R12C3
AE32
BB11
.
输出:
C12
R32C31
R11C54
备注:
每个坐标都是正确的。保证输入输出数据均在int范围内。输入输出数据字母部分均为大写。
(2)参考代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int a[N];
int main(){
int t;
cin>>t;
while(t--){
string s;
cin>>s;
int r,c;
r=s.find("R");
c=s.find("C");
if(r==0&&c!=0&&c!=-1&&s[c-1]>='0'&&s[c-1]<='9'){
int x,y;
x=stoi(s.substr(1,c-r-1));
y=stoi(s.substr(c+1));
stack<char> st;
while(y){
st.push((char)((y-1)%26+'A'));
y--;
y/=26;
}
while(!st.empty()){
cout<<st.top();
st.pop();
}
cout<<x<<endl;
}
else{
int mid;
for(int i=0;i<s.length();i++){
if(s[i]<='9'&&s[i]>='0'){
mid=i;
break;
}
}
string col=s.substr(0,mid);
int x,y;
x=stoi(s.substr(mid));
y=0;
for(int i=0;i<col.length();i++){
y*=26;
y+=(col[i]-'A'+1);
}
cout<<"R"<<x<<"C"<<y<<endl;
}
}
return 0;
}
5. MT2230 单条件和
(1)题目描述
“单条件”是数理逻辑中的5种常用连接词之一,记作“→”。它是二元运算。相当于“如果…那么……” 、“因为…所以……”、“只要…就……”等。也可称为“蕴涵”。“p→q”读作“如果p,那么q”,其中p称为前件,q称为后件。
其真值表如下:

如“异或和”为a0a20…can,我们现在要求“单条件和”,即a1→a2→…→an,对a1,a2…an作位意义上的单条件运算求和。
请按unsignedint类型进行运算。
格式
输入格式:
第一行一个整数n,表示有n个需要求单条件和的整数。第二行输入n个需要求单条件和的整数。
.
输出格式: 输出一个答案unsigned int类型整数。
样例1
输入:
10
1 2 3 4 5 6 7 8 9 10
.
输出: 4294967290
备注:
保证:对于100%的数据: 1<n ≤5,000,000。
(2)参考代码
#include<stdio.h>
const int N = 100005;
char ss[150];
unsigned int A[5000005];
int main()
{
int n;
int i=0,j=0;
scanf("%d",&n);
unsigned int v,ans=0;
for(i=0;i<n;++i){
scanf("%u",&v);
A[i] = v;
}
if(n==1){
printf("%d\n",A[0]);
return 0;
}
for(j=0;j<32;++j){
if(A[n-1] & (1<<j)){
ans |= (1<<j);
continue;
}
unsigned int v = (A[0]>>j) & 1;
for(i=1;i<n;++i){
unsigned int t = (A[i]>>j) & 1;
if(v==1 && t==0){
v = 0;
}else{
v = 1;
}
}
if(v){
ans |= (1<<j);
}
}
printf("%u\n",ans);
return 0; }
6. MT2231 lowbit
(1)题目描述
lowbit(z)是a的二进制表达式中最低位的1所对应的值(О无最低位1,规定lowbit(0)= 0 )。
请你编写lowbit(az)函数。
格式
输入格式:
第一行一个整数n表示数据组数。
接下来n行,每行(以十进制形式)输入一个整数(在int范围内)。
.
输出格式: 对于每组数据,将其输入的整数作为参数传入lowbit(a)函数,并(以十进制形式)输出lowbit(a)函数返回的值。
样例1
输入:
8
-1
0
1
2
3
4
5
6
.
输出:
1
0
1
2
1
4
1
2
备注:
保证:对于100%的数据:1≤n ≤1,000,000。
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int main( )
{
int n;
cin >> n;
for(int i = 0;i < n;i++){
int num = 0;
scanf("%d", &num);
printf("%d\n", num&(-num));
}
return 0;
}
7. MT2232 位运算
(1)题目描述

格式
输入格式:
第一行一个整数n。
第二行n个整数a[i]。
.
输出格式: 输出一行一个整数表示答案,即操作后所有数的平方和的最大值。
样例1
输入:
2
2 4
.
输出: 28
备注:
(2)参考代码
import time
from typing import List, Tuple
from collections import deque, Counter
from queue import PriorityQueue
import math
from functools import lru_cache
#from sortedcontainers import SortedDict, SortedSet
import random
import copy
import sys
sys.setrecursionlimit(999999999)
def main():
n = int(input())
arr = list(map(int, input().split()))
cnt = [0] * 32
for v in arr:
for b in range(32):
if v & (1 << b):
cnt[b] += 1
tot = 0
for _ in range(n):
val = 0
for i in range(32):
if cnt[i]:
cnt[i] -= 1
val |= (1 << i)
tot += val** 2
print(tot)
if __name__ == '__main__':
main();
8. MT2233 三进制计算机1
(1)题目描述
莫斯科国立大学研究员设计了第一批三进制计算机CeTyHb和CeTyHb70。设计计划由科学院院士C·几·Co6oneB在1956年发起。该计划旨在为大专院校、科研院所、设计单位和生产车间提供一种价廉物美的计算机。在头两年测试期,CeTyHb几乎不需要任何调试就运行得非常顺利,它甚至能执行一些现有的程序。1960年,CeTyHb开始公共测试。
1960年4月,CeTyHb就顺利地通过了公测。它在不同的室温下都表现出惊人的可靠性和稳定性。它的生产和维护也比同期其它计算机要容易得多,而且应用面广,因此CeTyHb被建议投入批量生产。
可是,苏联官僚对这个经济计划外的科幻产物持否定的态度且勒令其停产。而此时,对CeTyHb的订单却如雪片般从各方飞来,但30到50台的年产量远不足以应付市场需求。很快,计划合作生产CeTyHb的工厂倒闭了。1965年,CeTyHb停产了。取而代之的是一种二进制计算机,但价格却贵出2.5倍。
CeTyHb总共生产了150台(包括样机)。从加里宁格勒到雅库茨克,从阿什哈巴德到新西伯利亚,全苏都能看到CeTyHb的身影。各地都对CeTyHb的反应不错,认为它编程简单(不需要使用汇编语言),适用于工程计算、工业控制、计算机教学等各个领域。
有了CeTyHb的成功经验,研究员们决定不放弃三进制计算机的计划。他们在1970年推出了CeTyHb 70型计算机。CeTyHb 70对三进制的特性和概念有了进一步的完善和理解:建立了三进制字节——tryte (对应于二进制的byte),每个三进制字节由6个三进制位(trit,约等于9.5个二进制位bit)构成;指令集符合三进制逻辑;算术指令允许更多的操作数长——1、2和3字节(三进制),结果长度也扩展到6字节(三进制)。
对CeTyHb 70而言,传统计算机的字的概念已经失去意义了。编程的过程就是对三进制运算和三进制地址的操作。这些基于三进制字节的命令将会通过对虚拟指令的编译而得到。*
CeTyHb 70成了莫斯科国立大学三进制计算机的绝唱。由于得不到上级的支持,这个科研项目不得不无限期停顿下来。
三进制计算机,是以三进法数字系统为基础而发展的计算机。在光子计算机研究领域也有涉及。
三进制代码的一个特点是对称,即相反数的一致性,因此它就和二进制代码不同,不存在无符号数的概念。这样,三进制计算机的架构也要简单、稳定、经济得多。其指令系统也更便于阅读,而且非常高效。
在一般情况下,命题不一定为真或假,还可能为未知。在三进制逻辑学中,符号1代表真;符号-1代表假;符号0代表未知。这种逻辑表达方式更符合计算机在人工智能方面的发展趋势,它为计算机的模糊运算和自主学习提供了可能。
在本题中,请你将输入的对称三进制数转换为对应的十进制数。对称三进制数不是用0/1/2表示,比较特殊,是用1/0/-1表示,故名对称。本题中-1用符号’-‘表示,而1和0直接表示即可。
格式
输入格式:
第一行输入一个整数n,表示数据组数。
接下来n行,每行输入一个对称三进制整数。
.
输出格式:
对于第2~n+1行输入的每一个对称三进制整数,分别输出其十进制形式。
样例1
输入:
8
-0
-1
0
1
1-
10
1–
.
输出:
-3
-2
-1
0
1
2
3
5
备注:
样例中2=3-1,3=3+0*1,5=9-3-1。
保证:对于100%的数据: 1≤n ≤ 1,000,000,输入的对称三进制数对应的整数在int类型范围内。
(2)参考代码
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <string.h>
#include <algorithm>
#include <map>
#include <vector>
#include <algorithm>
#include <vector>
#include <set>
#include <queue>
#include <string>
#include <unordered_map>
#include <unordered_set>
using namespace std;
const int N = 100005;
char s[N];
int main(){
#ifdef TEST
freopen("/Users/grh/Programming/CLionProjects/AlgoCoding/input.txt", "r", stdin);
#endif
int n; scanf("%d", &n);
long long val;
for (int i = 0; i < n; i++) {
scanf("%s", s);
int len = strlen(s);
long long pow = 1;
long long ans = 0;
for (int i = len-1; i >= 0; i--) {
if (s[i] == '-') ans -= pow;
else if (s[i] == '1') ans += pow;
pow *= 3;
}
printf("%lld\n", ans);
}
return 0;
}
9. MT2234 三进制计算机2
(1)题目描述
三进制计算机,是以三进法数字系统为基础而发展的计算机。在光子计算机研究领域也有涉及。莫斯科国立大学研究员设计了第一批三进制计算机CeTyHb和CeTyHb70。
三进制代码的一个特点是对称,即相反数的一致性,因此它就和二进制代码不同,不存在无符号数的概念。这样,三进制计算机的架构也要简单、稳定、经济得多。其指令系统也更便于阅读,而且非常高效。
在一般情况下,命题不一定为真或假,还可能为未知。在三进制逻辑学中,符号1代表真;符号-1代表假;符号0代表未知。这种逻辑表达方式更符合计算机在人工智能方面的发展趋势,它为计算机的模糊运算和自主学习提供了可能。
在本题中,请你将输入的十进制数转换为对应的对称三进制数。对称三进制数不是用0/1/2表示,比较特殊,是用1/0/-1表示,故名对称,其中-1请用符号′-‘表示,而1和0直接表示即可。
格式
输入格式:
第一行输入一个整数n,表示数据组数。
接下来n行,每行输入一个十进制整数。
.
输出格式: 对于第2~n+1行输入的每一个十进制整数,分别输出其三进制形式。
样例1
输入:
8
-3
-2
-1
0
1
2
3
5
.
输出:
-0
-1
0
1
1-
10
1–
(2)参考代码
#include <cstdio>
using namespace std;
int main()
{
int n, len;
scanf("%d", &n);
while (n--)
{
int num, len = 0;
char str[256];
bool isNeg = false;
scanf("%d", &num);
if (num < 0)
{
isNeg = true;
num = -num;
}
do
{
int rem = num % 3;
num /= 3;
// 余数为2,本位变为‘-’
if (rem == 2)
{
str[len] = '-';
// 高一位加上1
num++;
}
else if (rem == 0)
str[len] = '0';
else if (rem == 1)
str[len] = '1';
len++;
} while (num > 0);
if (isNeg)
// 负数转换
for (int i = 0; i < len; i++)
if (str[i] == '-')
str[i] = '1';
else if (str[i] == '1')
str[i] = '-';
for (int i = len - 1; i >= 0; i--)
putchar(str[i]);
putchar('\n');
}
return 0;
}
10. MT2235 整数大小比较
(1)题目描述
给出两个正整数,判断他们的大小。
格式
输入格式: 两个正整数
.
输出格式:
若前者大,输出>
若后者大,输出<
若一样大,输出=
样例1
输入: 1412894619244619891 23762842222
.
输出: >
备注:
保证所有数在2的100次方以内
(2)参考代码
def main():
#code here
x, y = [int(i) for i in input().split()]
if x > y:
print(">")
elif x < y:
print("<")
else:
print("=")
pass
if __name__ == '__main__':
main();
11. MT2236 升级版斐波那契数列
(1)题目描述
我们都知道斐波那契数列一项是前两项的和,现在我们规定一个升级版斐波那契数列,一项为前三项的和,要求前n项的和。
格式
输入格式: 第一行包含一个数n
.
输出格式: 前n项的和
样例1
输入: 4
.
输出: 6
备注:
其中:4<n ≤1000
(2)参考代码
def main():
#code here
n = int(input())
a=1
b=1
c=1
ans=3
cnt=3
while cnt!=n:
d=a+b+c
ans+=d
a=b
b=c
c=d
cnt+=1
print(ans)
if __name__ == '__main__':
main();
12. MT2237 2的n次幂
(1)题目描述
任意给定一个正整数N(N ≤100),计算2的n次方的值。
格式
输入格式: 输入一个正整数N
.
输出格式: 输出2的N次方的值。
样例1
输入: 5
.
输出: 32
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int main( )
{
int n;
scanf("%d",&n);
double res = 1;
for(int i = 0;i <n;i++){
res*=2;
}
printf("%.00f",res);
return 0;
}
13. MT2238 大斐列
(1)题目描述
计算斐波那契数列第n项。

格式
输入格式: 一个整数n
.
输出格式: 一个整数F[n]
样例1
输入: 6
.
输出: 8
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+100;
int f[N][N];
void add(int a,int b,int c){
int carry=0;
for(int i=1;i<N;i++){
f[c][i]=f[a][i]+f[b][i]+carry;
carry=0;
if(f[c][i]>=10){
carry=1;
f[c][i]-=10;
}
}
}
int main( )
{
int n;
cin>>n;
f[1][1]=f[2][1]=1;
for(int i=3;i<=n;i++){
add(i-1,i-2,i);
}
int p=N-1;
while(f[n][p]==0) p--;
for(int i=p;i>=1;i--){
cout<<f[n][i];
}
cout<<endl;
return 0;
}
14. MT2239 个数统计
(1)题目描述
给你一个非负整数N,请求出他的阶乘N!中某个数a出现的次数m。
例如:N =5, a=1时,5! =120 ,故m=1。
格式
输入格式: 输入一行用空格隔开的两个非负整数,分别代表N和a。
.
输出格式: 输出一行一个正整数代表m。
样例1
输入: 6 2
.
输出: 1
备注:
其中:0≤n ≤1000,0 ≤a ≤9。
(2)参考代码
#include<bits/stdc++.h>
#define N 100000
using namespace std;
int length = 1, tmp, a[N];
void Mul(int n){ //高精乘
for(int i = 1 ; i <= n ; i++){
for(int j = 0 ; j < length ; j++){ //length表示为数组长度
tmp += a[j] * i; //tmp为当前结果与进位之和
a[j] = tmp % N; //每一个int数组里头,都存了一个小于N的整型
tmp /= N; //算出进位
if(tmp && j == length - 1) length++; //表明数组长度要进行扩增
}
}
}
int main(){
int n, m;
cin>>n>>m;
a[0] = 1; //初始化
Mul(n);
//用string保存答案
string str = "", s;
char tmp[N];
sprintf(tmp, "%d" , a[length - 1]); //利用sprintf将数字转为字符串,方便统计
s = tmp, str += s;
for(int i = length - 2; i >= 0 ; i--){
sprintf(tmp, "%05d" , a[i]); //利用sprintf将数字转为字符串,方便统计
s = tmp, str += s;
}
//计算结果
int sum = 0, len = str.length();
for(int i = 0 ; i < len ; i++){
if(str[i] - '0' == m) sum++;
}
printf("%d", sum);
}
15. MT2240 个数统计2
(1)题目描述
给你一个非负整数N,请求出他的阶乘N!中某个数b出现的次数m。
注意,判断时,不关注数字出现在哪一位,只关注数字是否一致。例如:N=5,b=12时,5!=120,故m=1
格式
输入格式: 输入一行用空格隔开的两个非负整数,分别代表N和b
.
输出格式: 输出一行一个正整数代表m
样例1
输入: 5 10
.
输出: 0
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int jie(int n,string b){
int static a[10000],i,j,l=0,s,res;
string str="";
a[0]=1;
for(int i=1;i<=n;i++){
s=0;
for(int j=0;j<=l;j++){
s=s+a[j]*i;
a[j]=s%10;
s/=10;
}
while(s){
l++;
a[l]=s%10;
s/=10;
}
}
for(int i=l;i>=0;i--){
str+=a[i]+'0';
}
int begin=-1;
while((begin=str.find(b,begin+1))!=string::npos) res++;
return res;
}
int main( )
{
int n,m;
string b;
cin >>n>>b;
m = jie(n,b);
cout<<m;
return 0;
}
16. MT2241 幸运数
(1)题目描述
小码哥的幸运数是7,他想知道n!中有几个幸运数。
比如12!= 479001600其中数字7出现的次数是1,所以有1个幸运数。
格式
输入格式: 一个整数n。
.
输出格式: 一个整数,表示幸运数个数
样例1
输入: 12
.
输出: 1
备注:
对于100%的数据0≤n ≤1000
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int jie(int n){
int static a[10000],i,j,l=0,s,res;
a[0]=1;
for(int i=1;i<=n;i++) {
s=0;
for(int j=0;j<=l;j++) {
s=s+a[j]*i;
a[j]=s%10;
s/=10;
}
while(s) {
l++;
a[l]=s%10;
s/=10;
}
}
for(int i=l;i>=0;i--){
if(a[i]==7) res++;
}
return res;
}
int main( )
{
int n,res;
cin >>n;
res = jie(n);
cout<<res;
return 0;
}
17. MT2242 num++
(1)题目描述
有一个长度为m+1的数列{ an},它长得十分随意。第一项值为1,接下来m项a= ag+ agy。现给出每一项的a, gy 求出数列接下来m项并输出。
格式
输入格式:
第一行一个正整数m,表示第1项之后的数列项数。
接下来m行,每行两个整数c, y表示这一项为第c项a。与第y项ay的和,保证α和 agy为已存在的项。
.
输出格式: m行。每行一个整数表示答案。
样例1
输入:
5
1 1
2 2
3 3
4 4
5 4
.
输出:
2
4
8
16
24
备注:
其中: m≤1000
(2)参考代码
def main():
a=[0,1]
x=[0,0]
y=[0,0]
n=int(input())
for i in range(2,n+2):
t,q=map(int,input().split())
x.append(t)
y.append(q)
for i in range(2,n+2):
a.append(a[x[i]]+a[y[i]])
print(a[i])
pass
if __name__ == '__main__':
main();
18. MT2243 A+B problem
(1)题目描述
计算A+B(1≤A,B≤1010000))要求使用struct 或 class并重载运算符。
格式
输入格式: 两行每行一个整数A,B
.
输出格式: 一个整数A+B
样例1
输入:
1
1
.
输出: 2
(2)参考代码
#include <bits/stdc++.h>
using namespace std;
class Num {
public:
Num(string s) {
for (int i = s.size() - 1; i >= 0; i--) {
A.push_back(s[i] - '0');
}
}
Num(vector<int> &A) {
this->A = A;
}
Num operator+(const Num &b) {
vector<int> C;
vector<int> A = this->getVector();
vector<int> B = b.getVector();
int t = 0;
for (int i = 0; i < A.size() || i < B.size() || t; i++) {
if (i < A.size())
t += A[i];
if (i < B.size())
t += B[i];
C.push_back(t % 10);
t /= 10;
}
Num c(C);
return c;
}
vector<int> getVector() const {
return A;
}
void print() {
for (int i = A.size() - 1; i >= 0; i--) {
printf("%d", A[i]);
}
}
private:
vector<int> A;
};
int main() {
string a, b;
vector<int> A, B;
cin >> a >> b;
Num numA(a);
Num numB(b);
Num numC = numA + numB;
numC.print();
return 0;
}
19. MT2244 A-B problem
(1)题目描述
计算A-B(A,B≤1010000)要求使用struct 或class并重载运算符。
格式
输入格式: 两行每行一个整数A,B
.
输出格式: 一个整数A-B
样例1
输入:
2
1
.
输出: 1
(2)参考代码
#include<iostream>
#include<cstring>
using namespace std;
int a[100000001],b[10000001],c[10000001],lena,lenb,lenc,i;
char n[100001],n1[100001],n2[100001];
int main()
{
scanf("%s",n1);
scanf("%s",n2);
if(strlen(n1)<strlen(n2)||(strlen(n1)==strlen(n2)&&strcmp(n1,n2)<0))//n1-n2<0的情况
{
strcpy(n,n1);
strcpy(n1,n2);
strcpy(n2,n);//变成n2-n1取负
cout<<"-";
}
lena=strlen(n1);lenb=strlen(n2);
for(i=0;i<=lena-1;i++)a[lena-i]=int(n1[i]-'0');
for(i=0;i<=lenb-1;i++)b[lenb-i]=int(n2[i]-'0');
i=1;
while(i<=lena||i<=lenb)
{
if(a[i]<b[i])
{//关键处,模拟竖式减法
a[i]+=10;
a[i+1]--;
}
c[i]=a[i]-b[i];
i++;
}
lenc=i;
while((c[lenc]==0)&&(lenc>1))lenc--;//最高位0判断
for(i=lenc;i>=1;i--)cout<<c[i];//倒序输出
cout<<endl;
return 0;
}
20. MT2245 求圆周率
(1)题目描述

格式
输入格式: 只有一行,一个整数n,表示圆周率精确到小数点后位数。
.
输出格式: 输出精确到第n位的Π。
样例1
输入: 10
.
输出: 3.1415926535
备注:
保证:对于100%的数据:0≤n ≤1,000。
(2)参考代码
#include <time.h>
#include <iostream>
#include <list>
#include<math.h>
using namespace std;
// 估测要计算的次数
int count(int n)
{
int i = 1;
double sum = 0;
int a, b;
while(1)
{
a = 2 * i + 1;
b = i;
sum = sum + log10(a / b);
i++;
if (sum > n + 1) {
return i;
}
}
}
int main()
{
// 定义我们需要多少个结点
#define NODE_NUM 1050
list<int> num(NODE_NUM, 0);// 存放R(n)
list<int> sum(NODE_NUM, 0);// 存放Sum(n)
int print;// 所需精度
cin >> print;
int cnt = count(print);// 所需迭代次数
// 我们直接将 R(1) 初始化为2,这样就可以免去后面再统一乘2
num.front() = 2;
sum.front() = 2;
// 这里循环的 i 就是 n
for (int i = 1; i <= cnt; ++i)
{
int ret = 0;// 记录进位,补位情况
// 计算R(n + 1)
// 计算 R(n) * n
for (list<int>::reverse_iterator cur1 = num.rbegin(); cur1 != num.rend(); cur1++)
{
// 每一位都是本位乘i,再加上进位
int val = *cur1 * i + ret;
// 保存进位
ret = val / 10;
// 保存本位
*cur1 = val % 10;
}
ret = 0;
// 计算 R(n) * n / (2n + 1)
for (list<int>::iterator cur1 = num.begin(); cur1 != num.end(); cur1++)
{
// 除数
int div = (i << 1) + 1;
// 加上前一位的余数
int val = *cur1 + ret * 10;
// 除法,保存本位
*cur1 = val / div;
// 保存余数
ret = val - *cur1 * div;
}
ret = 0;
// 计算 sum += R(n + 1)
for (auto cur2 = sum.rbegin(), cur1 = num.rbegin(); cur2 != sum.rend(); cur2++, cur1++)
{
// 大数加法
int val = *cur1 + *cur2 + ret;
*cur2 = val % 10;
ret = val / 10;
}
}
// 打印
if(print==0) cout<<sum.front();
else cout << sum.front() << '.';
list<int>::iterator it = sum.begin();
it++;
int i = 0;
while (i < print)
{
cout << *it;
it++;
i++;
}
return 0;
}
21. MT2246 派的n位
(1)题目描述
利用反三角函数幂级展开式来逼近pi的值。
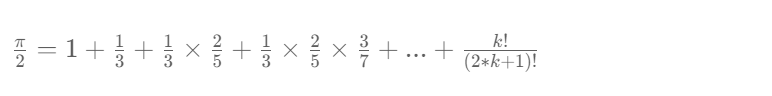
格式
输入格式: 第一行有一个数n,表示求到小数点n位(0-1000)
.
输出格式: 一行,输出保留到小数点n位的Π的表示
样例1
输入: 5
.
输出: 3.14159
(2)参考代码
#include <iostream>
#include <cstdio>
#include <string>
using namespace std;
int n;
string s="14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661300192787661119590921642019893";
int main(){
scanf("%d",&n);
if(n==0) printf("3");
else{
printf("3.");
for(int i=0;i<n;++i) cout<<s[i];
}
return 0;
}
22. MT2247 进行一个幂的运算
(1)题目描述
让我们来简单练习一下求幂。
给出m和k,求m的2的k次方-1次幂。答案对100000007取模。
格式
输入格式: 两个整数m, k,意义如题所示
.
输出格式: 一个整数表示答案
样例1
输入: 5 3
.
输出: 78125
备注:
数据范围:1≤m≤100000,0 ≤k ≤1000000
(2)参考代码
#include <iostream>
#define MOD 100000007
using namespace std;
long long fast_pow(int a, int b){
long long x = a; // 底数
long long res = 1; // 结果
while(b>0){
res=(res*x)%MOD;
b--;
x=(x*x)%MOD;
}
return res;
}
int main() {
long long p = 0;
long long ans = 0;
int m, k;
cin >> m >> k;
//m的2^k-1次方,m的指数用二进制表示为k个1,不必再判断指数的当前位置是0还是1
ans = fast_pow(m,k);
cout << ans << endl;
return 0;
}
23. MT2248 快速幂
(1)题目描述

格式
输入格式: 三个用空格隔开的整数a,b和c。
.
输出格式: 一个整数,表示a的b次 mod c 的值。
样例1
输入: 2 3 9
.
输出: 8
备注:
提示: 1≤a,b,c ≤10000000。
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int main( )
{
long long a,b,c;
cin>>a>>b>>c;
long long ans=1,base=a;
while(b!=0){
if(b&1!=0){
ans*=base;
}
ans%=c;
base*=base;
base%=c;
b>>=1;
}
cout<<ans;
return 0;}
24. MT2249 幂和
(1)题目描述

格式
输入格式: 一个正整数n
.
输出格式: 输出所求的值
样例1
输入: 3
.
输出: 32
备注:
n 100000。
(2)参考代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll MOD = 998244353;
ll solve(ll x) {
ll res = 1;
ll p = x;
while (p > 0) {
if (p & 1) res = (res * x) % MOD;
x = (x * x) % MOD;
p >>= 1;
}
return res;
}
int main() {
ll n;
cin >> n;
ll res = 0;
for (ll i = 1; i <= n; ++i) res = (res + solve(i)) % MOD;
cout << res;
return 0;
}
25. MT2250 Good Num的数量
(1)题目描述
Good Num的定义:数字下标从0开始,偶数下标处的数字都是偶数;奇数下标处的数字都是质数。
给定整数k,求解长度为k且是Good Num的数的数量。结果对109+7取模。请编写函数count来完成数量统计,传入参数k,最后返回取模之后的结果。
保证输入的都是正整数并且不考虑前导0。
格式
输入格式: 第一行一个整数k(1≤k ≤10的15次)。
.
输出格式: 输出取模之后的结果。
样例1
输入: 122222222222222
.
输出: 223203480
样例2
输入: 2
.
输出: 20
备注:
其中: 1≤k ≤10的15次
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
long long powmod(long long a,long long b,long long MOD)
{
a %= MOD;
long long ans = 1;
while(b>0) {
if(b&1)
ans = ans * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return ans;
}
int GoodNumbers(long long n)
{
long long ans = 1;
long long p4 = n/2;
long long p5 = n - p4;
long long MOD = 1e9 + 7;
ans = powmod(4,p4,MOD) % MOD * powmod(5,p5,MOD) % MOD;
ans %= MOD;
return (int)ans;
}
int main( )
{
long long k;
scanf("%lld", &k);
cout << GoodNumbers(k) << endl;
return 0;
}
结语
感谢大家一直以来的不断支持与鼓励,码题集题库中的进阶塔350题正在逐步更新,之后会逐步跟进星耀,王者的题,尽请期待!!!
同时,也希望这些题能帮助到大家,一起进步,祝愿每一个算法道路上的“苦行僧”们,都能够历经磨难,终成正果,既然选择了这条路,走到了这里,中途放弃,岂不是太过可惜?
另附中国计算机学会的杰出会员、常务理事轩哥博士的B站视频讲解链接https://space.bilibili.com/518554541/?spm_id_from=333.999.0.0,供大家更好的进行学习与刷题~( ̄▽ ̄~)~
愿你的结局,配得上你一路的颠沛流离。


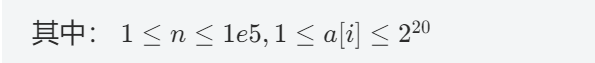

![[附源码]Python计算机毕业设计大学生网上书店Django(程序+LW)](https://img-blog.csdnimg.cn/7735b9ffca0e4919838935a3c8a49107.png)






![[附源码]Nodejs计算机毕业设计基于Java网上玩具商店Express(程序+LW)](https://img-blog.csdnimg.cn/5be6af9494634d168cf84b3ebcc3d9d4.png)