1. 方法原理

1.1 动机与贡献

摘要要点：基于盲点去噪的网络受网络设计和/或输入数据的影响会丢失部分信息 --> 有价值的信息损失会降低去噪的上限, 改进的方向:

• 引入一个全局感知的掩码映射，加速训练
• 使用一种 re-visible 的损失函数训练网络

改进的一些难点：

• 盲点占据数据的很大部分，预测像素点的感受野会丢失很多有价值的信息，降低网络性能
• 每次迭代中只优化部分像素会导致收敛变慢
• 很多工作对噪声对进行训练，要求噪声的分布是相同的

Blind2Unblind具体内容:

• 将每个噪声图像分块，并将每个快中的特定像素设置为盲点，得到了一个全局蒙版作为输入
• 将这些全局蒙版作为一个batch输入到网络之中
• 全局映射器对盲点位置的噪声体进行采样，投影到同一个平面上进行去噪

---

小结

• 动机：Noise2Void 盲点网络可以避免恒等映射，但是会损失信息，从而影响去噪的效果

• 挑战：如何将不可见的盲点转换为可见的盲点？既能利用盲点结构去噪，也能利用全部的信息提高性能

• 贡献：

  1. 提出了一种新的自监督去噪框架，使盲点位置像素可见，无需子样本，噪声模式先验和恒等映射。
  2. 提供了re-visible 损失的理论分析，给出了这种损失收敛的上限和下限

---

1.2 方法细节

(1) Noise2Void

N2V目标是最小化 $$\underset{\theta }{\mathrm{argmin}}{E}_y||f_{\theta }(y_{RF(i)})-y_i|{|}_2^2$$

这里的$f_{\theta }(.)$就是去噪网络，$y_{RF(i)}$是去噪中心i附近的patch，$y_i$是中心像素点。

注意该方法的强假设条件：

• 信号是不相互独立的
• 给定信号的条件下，噪声是相互独立的
• 噪声的均值是0

(2) re-visible without identity mapping

从多任务中借鉴其优化目标
$$\underset{\theta }{\mathrm{argmin}}{E}_y||h(f_{\theta }({\Omega }_y))-y|{|}_2^2+\lambda .||f_{\theta }(y)-y|{|}_2^2$$

其中，${\Omega }_y$表示掩码体；$h(.)$是一个全局感知掩码映射器，用于对盲点所在的去噪像素进行采样，λ 是一个常数。

用L1范数表示
$$\underset{\theta }{\mathrm{argmin}}||h(f_{\theta }({\Omega }_y))-y|{|}_1+\lambda .||{\hat{f}}_{\theta }(y)-y|{|}_1$$

其中，${\hat{f}}_{\theta }(y)$ 不需要求梯度，对梯度没有贡献。

那么优化目标可以构建为
$$\underset{\theta }{\mathrm{argmin}}|||h(f_{\theta }({\Omega }_y))-y|+\lambda .|{\hat{f}}_{\theta }(y)-y||{|}_2^2$$

转换一下变为损失函数的形式
$$\begin{array}{rl}\mathrm{T}(y)& =|||h(f_{\theta }({\Omega }_y))-y|+\lambda .|{\hat{f}}_{\theta }(y)-y||{|}_2^2\\ & =||h(f_{\theta }({\Omega }_y))-y|{|}_2^2+{\lambda }^2||{\hat{f}}_{\theta }(y)-y|{|}_2^2+2\lambda ||(h(f_{\theta }({\Omega }_y))-y).({\hat{f}}_{\theta }(y)-y)|{|}_1\end{array}$$

然后又根据一些推导分析，得到了 re-visible的最大似然形式（没太仔细推导）

$$\underset{\theta }{\mathrm{argmin}}{E}_y||h(f_{\theta }({\Omega }_y))+\lambda {\hat{f}}_{\theta }(y)-(\lambda +1)y|{|}_2^2$$

最后化的去噪结果是

$$\hat{x}=\frac{h(f_{\theta }^{\ast }({\Omega }_y))+\lambda {\hat{f}}_{\theta }^{\ast }(y)}{\lambda +1}$$

(3) 综合说明

具体说明：
将一个含有噪声的输入图片y分为两个分支进行处理

1. 上面一个分支

   • 上面的分支将y输入到 Global masker中，该模块将图像都划分为2*2的小块(示例)，然后在每个小块中分别mask 左上、左下、右上、右下的像素，形成4个盲点图像（即每张图片被mask掉25%的区域）
   • 将mask的图像输入到U-Net网络之中，预测被mask掉的区域
   • 经过Global mask mapper，把每张图被mask的25%区域的聚合形成一张去噪后的图像
   • 

2. 下面一个分支：

   • 直接将又噪声的数据输入到U-Net之中，用来弥补网络信息确实的问题。
   • 为了避免网络学到恒等映射，这个部分不进行梯度反传。

需要注意的是，存粹的re-visible损失只有一个变量，可以用来反传优化盲点项和visible项目，其优化过程非常不稳定，所以作者在实现的实现的时候加入了一个正则项约束这个过程。用损失函数来看就是下面着两个部分
$$\begin{array}{rl}L& =L_{rev}+\eta .L_{reg}\\ & =||h(f_{\theta }({\Omega }_y))+\lambda {\hat{f}}_{\theta }(y)-(\lambda +1)y|{|}_2^2+\eta .||h(f_{\theta }({\Omega }_y))-y|{|}_2^2\end{array}$$

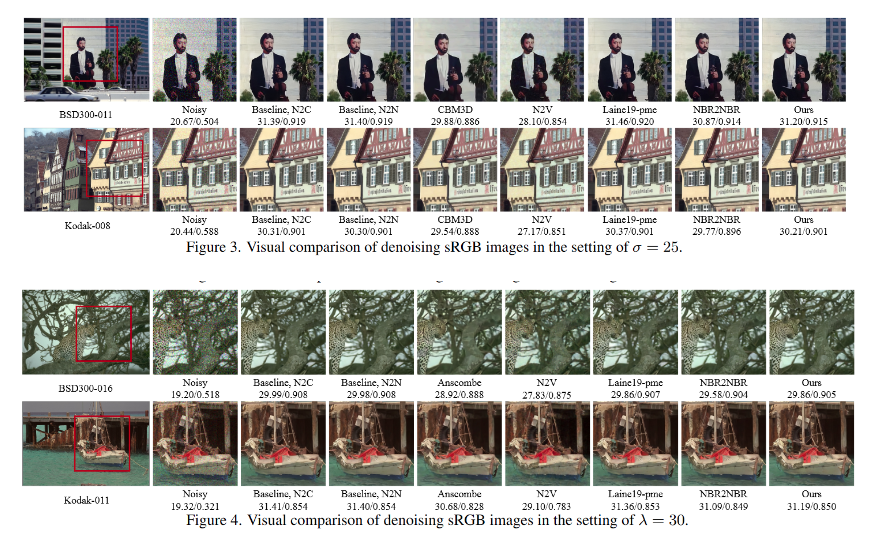
2. 效果

不同方法对比

3. 总结

1. 在Noise2Void 盲点网络的基础上实现了既要又要：既要盲点网络，又要被盲点位置上的原始信息
2. 零均值、噪声独立等假设仍然限制这一流派在实际噪声数据应用时的泛化性