算法竞赛入门【码蹄集进阶塔335题】(MT2126-2150)
文章目录
- 算法竞赛入门【码蹄集进阶塔335题】(MT2126-2150)
- 前言
- 为什么突然想学算法了?
- 为什么选择码蹄集作为刷题软件?
- 目录
- 1. MT2126 奇偶序列
- 2. MT2127 数组扦插
- 3. MT2128 sort
- 4. MT2129 NPU大赛
- 5. MT2130 逆序对
- 6. MT2131 随机排序
- 7. MT2132 不定区间排序
- 8. MT2133 栈的min
- 9. MT2134 括号家族
- 10. MT2135 五彩斑斓的世界
- 11. MT2136 栈间
- 12. MT2137 双端队列
- 13. MT2138 队列操作
- 14. MT2139 挑选
- 15. MT2140 合并货物
- 16. MT2141 合并石子
- 17. MT2142 第k小函数值
- 18. MT2143 大约
- 19. MT2144 事务处理
- 20. MT2145 前k小数
- 21. MT2146 前k小数(进阶)
- 22. MT2147 数列最大数
- 23. MT2148 一样的虫子
- 24. MT2149 完美数对
- 25. MT2150 AB数对
- 结语
前言

为什么突然想学算法了?
> 用较为“官方”的语言讲,是因为算法对计算机科学的所有分支都非常重要。 在绝大多数的计算机科学分支领域中,要想完成任何实质性的工作,理解算法的基础知识并掌握与算法密切相关的数据结构知识是必不可少的。
> 但从实际而言,是因为当下快到了考研和找工作的年纪(ಥ_ಥ),无论走哪一条路,都不免需要一些相对丰富的算法知识,是故,便产生了一个暑假速成算法的计划,可能对于像我这种算法竞赛小白而言,几乎很难,但我仍然还是想尝试一下,毕竟,梦想还是要有的,万一实现了呢?~( ̄▽ ̄~)~

为什么选择码蹄集作为刷题软件?
码蹄集,是在全国高等学校计算机教学与产业实践资源建设专家委员会(TIPCC) 指导下建设的,其依托全国各大名校计算机系和清华大学出版社等单位的强大资源,旨在为计算机学习爱好者提供全面和权威的计算机习题。
目录
1. MT2126 奇偶序列
(1)题目描述
给定n个数的数组,奇数和偶数分别排序(即所有奇数占的空位和偶数占的空位不变)
格式
输入格式:
输入一个正整数n
第二行输入n个数ai
.
输出格式: 输出排好序的数组。
样例1
输入:
5
3 4 1 5 2
.
输出: 1 2 3 5 4
备注:
其中: 1≤n ≤10000,1 ≤ai ≤100000
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100;
int a[N];
int ans[N];
vector<int> odd,even;
int main( )
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
ans[i]=a[i]&1;
if(ans[i]) odd.push_back(a[i]);
else even.push_back(a[i]);
}
sort(odd.begin(),odd.end());
sort(even.begin(),even.end());
int p1=0,p2=0;
for(int i=1;i<=n;i++){
if(ans[i]) cout<<odd[p1++]<<" ";
else cout<<even[p2++]<<" ";
}
cout<<endl;
return 0;
}
2. MT2127 数组扦插
(1)题目描述
给定n个数的数组,前半段升序排序记为a,后半段逆序排序b;,若为奇数中间那个数不动
然后将bi数组扞插到a中,形成交替结构,即:
ab1ap b2 agbR . … . … . … . … . … . … . … . … . … .c( c是中间那个数,如果数组长度是偶数,那么c不存在)
格式
输入格式:
输入一个正整数n
第二行输入n个数w;
.
输出格式:
输出排好序的数组。
样例1
输入:
5
1 2 3 4 5
.
输出: 1 5 2 4 3
备注:
其中: 1<n ≤10000,1 ≤ wi≤100000
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n, c = 0;
cin >> n;
vector<int>a(n/2);
for (int i = 0; i < n / 2; i++) {
cin >> a[i];
}
if (n % 2 != 0) {
cin >> c;
}
vector<int>b(n/2);
sort(a.begin(), a.end());
for (int i = 0; i < n / 2; i++) {
cin >> b[i];
}
sort(b.begin(), b.end(), greater<int>());
for (int i = 0; i < n / 2; i++) {
cout << a[i]<<" "<<b[i]<<" ";
}
if (n % 2 != 0) {
cout<< c;
}
}
3. MT2128 sort
(1)题目描述
或许在某个平行宇宙,会存在一种语言,使用的字母和英语一样,但字典序不一样。
给出一个字典序和一个字符串,将字符串按新字典序排序。
格式
输入格式:
第一行26个互不相同的小写字母,表示新型字典序。
第二行一个字符串,表示待排序字符串。
.
输出格式: 一个字符串代表答案。
样例1
输入:
qwertyuioplmnbcxzasdfghjkl
peace
.
输出: eepca
备注:
数据范围:
1≤字符串长度≤100000
字符串只包含小写字母
(2)参考代码
// 编写一个判断子串的函数
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
bool checkInclusion(string s1, string s2) {
if(s1.size()>s2.size())return false; //剪枝,如果s1.size()>s2.size(),直接返回false;
vector<int>a1(26,0),a2(26,0); //申请两个容器;
for(int i=0;i<s1.size();i++){
a1[s1[i]-'a']++;
a2[s2[i]-'a']++; //把s1和s2装入容器中;
}
if(a1==a2)return true; //如果相等,直接返回true;
for(int i=s1.size(),j=0;i<s2.size();i++,j++){ //滑动窗口部分。
a2[s2[j]-'a']--;
a2[s2[i]-'a']++;
if(a1==a2)return true;
}
return false;
}
int main(){
string s1,s2;
cin>>s1;
cin>>s2;
if(checkInclusion(s1,s2)) printf("true");
else printf("false");
return 0;
}
4. MT2129 NPU大赛
(1)题目描述
有n个人参加一场比赛,其中分数排名前k位的人将被选入下一轮(选入下一轮的人分数必须为正),特别的,如果几个人分数相同且刚好并列处于第k名(或是并列k-i名,但是全部算入后选入下一轮的人数超过k人),这几个人都将被选入下一轮,小码哥要求你输出进入下一轮的人数。
格式
输入格式:
输入一共2行:
第1行是两个数n,k,分别代表参加比赛的人数和预计将会进入下一轮的人数;1≤k ≤n ≤1e5
第2行有n个数,分别参加比赛的人的分数a1, a2,. . . , (n 。0≤a≤100
.
输出格式: 输出进入下一轮的人数。
样例1
输入:
8 5
7 5 10 7 9 8 7 5
.
输出: 6
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int nums[100003];
bool cmp(int a,int b){
return a>b;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,k,index=1,res=1;
cin>>n>>k;
for(int i=0;i<n;++i){
cin>>nums[i];
}
sort(nums,nums+n,cmp);
if(nums[0]==0) res=0;
for(int i=1;i<n;++i){
if(nums[i]==0) break;
if(nums[i]<nums[i-1]){
if(res>=k||index==k) break;
++index; //名次计数+1
}
++res; // 人数+1
}
cout<<res;
return 0;
}
5. MT2130 逆序对
(1)题目描述
给你一个长度为n的序列,有m次操作。每次翻转[l,r]的区间,每次操作后询问序列逆序对个数的奇偶性。
格式
输入格式:
第1行,有1个正整数,为原序列的长度n
第2行,有n个自然数,表示该序列的元素ai
第3 行,有1个正整数,为操作次数m
接下来m行,每行两个整数l, r,表示翻转的区间
.
输出格式: m行,每行表示每次问询的结果
样例1
输入:
3
1 2 3
2
1 2
2 3
.
输出:
odd
even
(2)参考代码
#include<iostream>
using namespace std;
int n,nums[10010],temp[10010],tree[10010];
int lowbit(int x){
return x&-x;
}
void add(int x,int t){
for(;x<=n;x+=lowbit(x)){
tree[x]+=t;
}
}
int get(int x){
int res=0;
for(;x>0;x-=lowbit(x)){
res+=tree[x];
}
return res;
}
void MergeSortArr(int arr[],int left,int mid,int right){//该函数同于将两个有序列合并成一个有序列,同时当两个有序列都为同一个元素是一样可以处理
int i = left,j = mid + 1;//两个索引用来遍历两个有序列
int k=0;//k用来遍历暂存数组temp
int temp[right-left+1];//开一个数组暂时存放
while(i <=mid && j <= right){//对两个有序列进行遍历排序,有一个序列遍历完成结束循环
if(arr[i] < arr[j])
temp[k++] = arr[i++];
else
temp[k++] = arr[j++];
}
while(i <= mid){//将另外一个没有遍历完全的有序列全部插入到temp中
temp[k++] = arr[i++];
}
while(j <= right){
temp[k++] = arr[j++];
}
//!!这里需要注意循环的条件里面不能使用left因为left的值在改变
for(i = 0;i < k;i++)//将排好序的序列更新到目标数组中
arr[left++] = temp[i];
}
//递归方法
void MergeSort(int arr[],int left,int right){
if(left == right)//如果两个划分为同一元素,递归结束
return ;
int mid = (left + right) / 2;//对本个划分再次进行划分
MergeSort(arr, left, mid);//对左边的序列进行划分此条命令结束代表左边的序列已经有序
MergeSort(arr, mid+1, right);//对右边的序列进行划分此条命令结束代表右边的序列已经有序
MergeSortArr(arr, left, mid, right);//和并两个序列
}
int main(){
cin>>n;
for(int i=1;i<=n;++i){
cin>>nums[i];
temp[i] = nums[i];
}
MergeSort(temp,1,n+1);
int cnt = 0;
for(int i=1;i<=n;i++){
int idx = lower_bound(temp+1, temp+n+1, nums[i])-temp;
add(idx,1);
cnt+= i-get(idx);
}
bool isOdd = cnt&1;
int q;
cin>>q;
while(q--){
int l,r;
cin>>l>>r;
cnt = (r-l)*(r-l+1)/2;
isOdd ^= cnt&1;
cout<<(isOdd ?"even":"odd")<<endl;
}
}
6. MT2131 随机排序
(1)题目描述
期末考试结束了,老师需要对繁多的学生按成绩进行排序来了解每个学生的学习情况,有些时候他需要将一些特定的学生放在一起进行排序,请你帮帮他。
每个学生将给出学号和总成绩,将给出的学生按照总成绩的降序排列,成绩相同按照学号升序排列。
格式
输入格式:
第一行输入一个正整数n,代表学生总个数。
接下来n行每行两个用空格隔开的正整数,分别代表学生的学号与其总成绩。
第n+2行输入一个正整数m,代表所询问的总次数。
接下来m行每行代表一次询问,每次询问有若干个正整数代表需要放在一起进行排列的学生的学号,以O作为结束标志。
.
输出格式: 依次对于每次询问输出一行用空格隔开的若干个正整数,代表按照要求进行排序的结果(只需输出学号)
样例1
输入:
2
1 360
2 361
1
1 2 0
.
输出: 2 1
(2)参考代码
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <string.h>
#include <algorithm>
#include <map>
#include <vector>
#include <algorithm>
#include <vector>
#include <set>
#include <queue>
#include <string>
#include <unordered_map>
#include <unordered_set>
using namespace std;
const int N = 100005;
int score[N];
struct node {
int idx, s;
bool operator < (const node& o) const {
if (s != o.s) return s > o.s;
return idx < o.idx;
}
};
int main(){
#ifdef TEST
freopen("/Users/grh/Programming/CLionProjects/AlgoCoding/input.txt","r", stdin);
#endif
int n; scanf("%d", &n);
int idx, s;
for (int i = 0; i < n; i++) {
scanf("%d %d", &idx, &s);
score[idx] = s;
}
int m; scanf("%d", &m);
vector<node> v; v.reserve(n);
for (int i = 0; i < m; i++) {
v.clear();
while (1) {
scanf("%d", &idx);
if (!idx) break;
v.push_back({idx, score[idx]});
}
sort(v.begin(), v.end());
for (auto& ins : v) {
printf("%d ", ins.idx);
}
printf("\n");
}
return 0;
}
7. MT2132 不定区间排序
(1)题目描述
又是一年年终,小码哥开始对手下员工的业绩进行考察。给出每个员工的编号与本年度他的表现评分,你需要帮助小码哥按部门对员工进行考核,每个部门员工的编号都在一个固定的区间内,由于部门之间的工作并不是独立的,有的员工会参加多个部门,所以区间可能会有重合。员工的编号保证唯一。
请将每个部门的员工按照表现评分的降序排列,评分相同按照编号的升序排列。
格式
输入格式:
第一行输入一个正整数n,代表员工总个数。
接下来n行每行两个用空格隔开的正整数,分别代表员工编号与其年度评分。
第n+2行输入一个正整数m,代表所询问的总次数(即部门数)。
接下来m行每行两个用空格隔开的正整数分别代表每个部门员工编号区间的左右端点,区间为闭区间。(即若有一行为100200,则100和200也为当前部门的员工)
.
输出格式: 依次对于每次询问输出一行用空格隔开的若干个正整数,代表按照要求进行排序的结果((只需输出员工编号)
样例1
输入:
2
100001 39
100002 486
1
100001 100002
.
输出: 100002 100001
备注:
员工编号从100001开始连续增加(即编号为100001、100002.100003…)
n≤1000001≤评分≤1000
每个部门人数不超过1000人,不超过1000个部门
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
struct employee{
int no;
int sc;
}emp[maxn];
bool cmpno(employee a,employee b){
return a.no<b.no;
}
bool cmp(employee a,employee b){
if(a.sc==b.sc)return a.no>b.no;
else return a.sc<b.sc;
}
int n,m;
void query(){
int l,r;
cin>>l>>r;
l-=1e5;
r-=1e5;
priority_queue<employee,vector<employee>,decltype(&cmp)>q(cmp);
for(int i=l;i<=r;i++){
assert(i+1e5==emp[i].no);
q.push(emp[i]);
}
while(!q.empty()){
cout<<q.top().no<<" ";
q.pop();
}
cout<<endl;
return;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>emp[i].no>>emp[i].sc;
}
sort(emp+1,emp+1+n,cmpno);
//for(int i=1;i<=n;i++)cout<<emp[i].no;
cin>>m;
while(m--){
query();
}
}
8. MT2133 栈的min
(1)题目描述
小码哥又被安排任务了,这次他需要要设计一个堆栈,他除了可以满足正常的栈的操作以外,还要可以输出栈内最小元素值。
o(n)的算法小码哥当然会,小码哥为了给上司一个惊喜决定设计一个o(1)就能输出的程序,自然这个任务就被丢给你了。
c(x)-将元素x插入栈中
y()-移除栈顶元素
s()-得到栈顶元素
g_m()-得到栈中最小元素
格式
输入格式:
第一行输入操作个数n(整数);
第2行到第n+1行输入一个整数t分别依次代表上述4种操作当t ==1时,会额外输入一个整数x;
.
输出格式: 当t ==3或t == 4时,输出相应数据,每一行输出一个数据
样例1
输入:
6
1 3
1 4
3
4
2
3
.
输出:
4
3
3
备注:
提示
(t≥1&& t≤4)
操作命令总数[0,100]
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int total;
int sk[1000010];
int main( )
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
int t;
scanf("%d",&t);
if(t==1){
int x;
scanf("%d",&x);
sk[++total] = x;
}else if(t==2){
if(total>=1) total--;
}else if(t==3){
printf("%d\n",sk[total]);
}else{
int ans = 1e9;
for(int i=1; i<=total;i++) ans = min(ans,sk[i]);
printf("%d\n",ans);
}
}
return 0;
}
9. MT2134 括号家族
(1)题目描述
小码哥在研究只由左括号和右括号组成的序列
给出一个括号序列,求出最长合法子串和它的数量。合法的定义:这个序列中左右括号匹配
例如:“(()”不合法,“)()(”也不合法,但“()()”和”(())”合法。
格式
输入格式: 输入一行只由左括号和右括号组成的序列(只包含小括号)
.
输出格式: 输出两个数字:最长子字符串的长度,以及此类子字符串的数量的等级。如果没有这样的子字符串,则输出“0 1”。
样例1
输入: ()()))()()(()
.
输出: 4 2
备注:
字符串长度小于等于10的6
(2)参考代码
#include <bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int N = 1e6 + 5;
const int mod = 1e9 + 7;
const double eps = 1e-8;
const double PI = acos(-1.0);
#define lowbit(x) (x & (-x))
int a[N];
int main()
{
std::ios::sync_with_stdio(false);
string s;
cin >> s;
stack<int> st;
int l = s.length();
for (int i = 0; i < l; i++)
{
if (s[i] == '(')
st.push(i);
else
{
if (st.size())
a[st.top()] = a[i] = 1, st.pop();
}
}
int mx = 0, cnt = 0;
map<int, int> mp;
for (int i = 0; i < l; i++)
{
if (a[i])
{
cnt++;
}
else
{
if (cnt >= mx)
{
mx = cnt;
mp[mx]++;
}
cnt = 0;
}
}
if (cnt >= mx)
mx = cnt, mp[mx]++;
if (mx == 0)
mp[mx] = 1;
cout << mx << " " << mp[mx] << endl;
return 0;
}
10. MT2135 五彩斑斓的世界
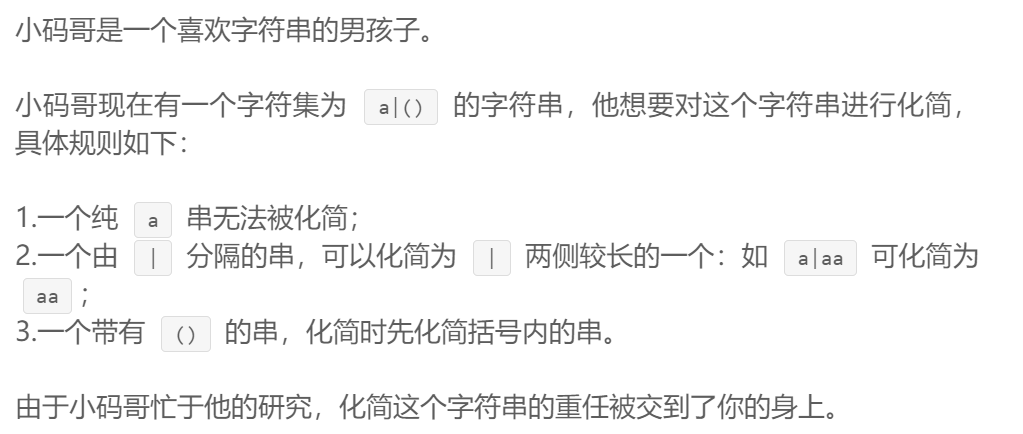
(1)题目描述
格式
输入格式: 输入一个字符集为al)的字符串,为你需要化简的字符串。
.
输出格式: 由于化简后的字符串字符集仅为a,你只需要输出化简后字符串的长度即可。
样例1
输入: aa(aa)|(aa|(a|aa))aa
.
输出: 4
备注:
测试数据保证括号匹配,且 | 两侧与括号内均不会出现空串。测试数据保证输入的字符串长度不超过105。
(2)参考代码
#include<iostream>
#include<cstdio>
#include<bits/stdc++.h>
#include<cstdio>
#include<algorithm>
using namespace std;
char ch;
int query()
{
int ans = 0, num = 0;
while (true)
{
ch = getchar();
if (ch == 'a') ++num;
else
if (ch == '(') num += query();
else
if (ch == ')') return ans = max(ans, num);
else
if (ch == '|') ans = max(ans, num), num = 0;
else
if (ch == EOF) return ans = max(ans, num);
}
}
int main()
{
cout<<query()<<endl;
return 0;
}
11. MT2136 栈间
(1)题目描述

格式
输入格式:
第一行输入一个整数n,表示操作个数。
接下来n行,每行输入一个操作,格式如题目描述中所示。
.
输出格式: 对于每个操作2和3,输出一行一个整数表示答案。
样例1
输入:
7
1 1
1 4
1 3
2
3 1
4
2
.
输出:
3
4
4
备注:
保证:对于100%的数据: 1≤n ≤5,000,000, 在int类型范围内,数列为空时只进行操作1,进行操作3时一定能访问到栈内元素。
(2)参考代码
#include <bits/stdc++.h>
#define ll long long
#define DEBUG 112412
using namespace std;
const int maxn = 5e6 + 55;
int a[maxn];
int main(){
#if DEBUG==1
freopen(“1”,”r”,stdin);freopen(“2”,”w”,stdout);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
int cnt = 0;
int n;
cin >> n;
for (int i = 1; i <= n; ++i){
int op;
cin >> op;
if (op == 1){
int x;
cin >> x;
a[++cnt] = x;
}
else if (op == 2){
cout << a[cnt] << '\n';
}
else if (op == 3){
int x;
cin >> x;
cout << a[x + 1] << '\n';
}
else{
cnt--;
}
}
}
12. MT2137 双端队列
(1)题目描述
小码哥想创建一个双端队列,即,两头都能进,两头都能访问,两头都能出。请你创建一个这样的双端队列并帮他实现以下操作:
1 x//将整数x增加到头部
2x//将整数x增加到尾部
3/访问头部的元素
4|/访问尾部的元素
5//弹出(删除)头部的元素
6//弹出(删除)尾部的元素
这个双端数列一开始是空的。
格式
输入格式:
第一行输入一个整数n,表示操作个数。
接下来n行,每行输入一个操作,格式如题目描述中所示。
.
输出格式: 对于每个操作3和4,输出一行一个整数表示答案。
样例1
输入:
11
1 3
1 6
2 9
3
4
5
2 7
2 8
6
3
4
.
输出:
6
9
3
7
备注:
保证:对于100%的数据: 1≤n ≤1,000,000, a在int类型范围内,数列为空时只进行操作1和2。
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int main( )
{int n,op,x,length;
deque<int> ideq;
cin >>n;
while(n--){
scanf("%d", &op);
if (op == 1) {
scanf("%d", &x);
ideq.push_front(x);
}
else if (op == 2) {
scanf("%d", &x);
ideq.push_back(x);
}
else if (op == 3) printf("%d\n", ideq.front());
else if (op == 4) {
length=ideq.size();
printf("%d\n", ideq.back());
}
else if (op == 5) ideq.pop_front();
else ideq.pop_back();
}
return 0;
}
13. MT2138 队列操作
(1)题目描述
给定n,m,q, u , v, t,6个值。
给定一个数组a[N],长度为n,你有m次操作机会,每一次可以取出数组中最大的值x,使其分为【px】,和x - 【px】两部分,加入数组当中。
p = u / v,【×】符号表示对x向下取整。
你每操作一次,数组中所有除了被你取出的最大值的数以外,都要加上q;
当你操作完成m次后,你需要知道,现在在数组中n+m个数的数值;并且知道每一次你操作的对象的值;
为了减少输出量,我们引入整数t,按照输出格式输出。
格式
输入格式:
第一行包含六个整数n,m,q,u, v, t, t将在输出格式中展示其意义,其余数已在上述题面中解释意义。
第二行包含n个非负整数,为a1, a2,…, an,即初始时数组中元素的值。
同一行中相邻的两个数之间,恰好用一个空格隔开。
.
输出格式:
第一行输出【m/t】个整数,按时间顺序,依次输出第t 次,第2t次,第3t次…操作对象的元素值。
第二行输出【 (n+m)/t】个整数,输出m次操作后数组中的元素;需要按从大到小的顺序,依次输出排名第t,第2t,第3t…的元素。
样例1
输入:
3 7 1 1 3 1
3 3 2
.
输出:
3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2
(2)参考代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,q,u,v,t;
int h1,h2,h3,t1,t2,t3;
int q1[8000001],q2[8000001],q3[8000001];
int cmp(int a,int b){
return a>b;
}
int pop1(int time){
int top1=-1,top2=-1,top3=-1;
if(h1<=t1){
top1=q1[h1]+(time-1)*q;
}
if(h2<=t2){
top2=q2[h2]+(time-h2-1)*q;
}
if(h3<=t3){
top3=q3[h3]+(time-h3-1)*q;
}
int k=1;
if(top1<top2){
k=2;
}
if(top3>max(top1,top2)){
k=3;
}
switch(k){
case 1:h1++;return top1;break;
case 2:h2++;return top2;break;
case 3:h3++;return top3;break;
}
}
void push1(int x){
int p1=1LL*x*u/v;
int p2=x-p1;
if(p1<p2){
swap(p1,p2);
}
q2[++t2]=p1;
q3[++t3]=p2;
}
int main(){
scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t);
for(int i=1;i<=n;i++){
scanf("%d",&q1[i]);
}
sort(q1+1,q1+n+1,cmp);
h1=1;
h2=1;
h3=1;
t1=n;
t2=0;
t3=0;
int top;
for(int i=1;i<=m;i++){
top=pop1(i);
if(i%t==0){
printf("%d ",top);
}
push1(top);
}
printf("\n");
for(int i=1;i<=n+m;i++){
top=pop1(m+1);
if(i%t==0){
printf("%d ",top);
}
}
return 0;
}
14. MT2139 挑选
(1)题目描述
小码哥这一阵子心情不太好,老是想着一些稀奇古怪的问题来刁难下属,今天派你去挑选甜品,甜品可以通过甜度来区分。总共有n个甜品,( n为奇数),他要求你初始拾取一个,之后每一次按顺序拿两个,每拿两个就把这些序列中的中位数的甜点标记出来,直到拿完。
请你挑出被标记过的甜点的甜度(按升序排列;相同的甜度不用重复输出)。按给出的数组顺序拾取,从1到n逐个拾取。
格式
输入格式:
第一行一个整数n
第二行n个整数,空格分隔,表示甜点的甜度
.
输出格式: 输出标记过的甜点的甜度,空格分隔,升序排列
样例1
输入:
5
1 2 3 4 5
.
输出: 2 3
备注:
提示:3≤n ≤1000000
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
class MedianFinder{
private:
priority_queue<double,vector<double>, greater<double>> big_heap;//大顶堆
priority_queue<double,vector<double>, greater<double>>small_heap;//小顶堆
public:
void addNum(int num) {
if (big_heap.empty()){
big_heap.push(num);
}else if(big_heap.size()==small_heap.size()){
if (num<big_heap.top()){
big_heap.push(num);
}else{
small_heap.push(num);
}
}else if(big_heap.size()>small_heap.size()){
if (num>big_heap.top()){
small_heap.push(num);
}else{
small_heap.push(big_heap.top());
big_heap.pop();
big_heap.push(num);
}
}else if(big_heap.size()<small_heap.size()){
if (num<small_heap.top()){
big_heap.push(num);
}else{
big_heap.push(small_heap.top());
small_heap.pop();
small_heap.push(num);
}
}
}
double findMedian() {
if (big_heap.size()==small_heap.size()){
return (big_heap.top() + small_heap.top()) / 2;
}else if(big_heap.size()>small_heap.size()){
return big_heap.top();
}
return small_heap.top();
}
};
int n,a;
set<int> s;
int main( ){
MedianFinder m;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a;
m.addNum(a);
if(i%2&&i!=1){
s.insert(m.findMedian());
}
}
for (auto it = s.cbegin(); it != s.cend(); it++){
printf("%d ",*it);
}
return 0;
}
15. MT2140 合并货物
(1)题目描述
小码哥又被派来合并货物了,最近公司接受了一大笔货物,现在已经按照不同的种类分成许多堆,相同种类的货物在同一堆,小码哥决定把他们合并来方便运输。
每一次合并,小码哥可以把两堆货物合并到一起,消耗的体力等于两堆货物的重量之和。可以看出,所有的货物经过n-1次合并之后,就只剩下一堆了。小码哥在合并货物时总共消耗的体力等于每次合并所耗体力之和。
因为小码哥不可以耗费太多的体力来干这种事情,所以小码哥在合并货物时要尽可能地节省体力。这些货物的重量都为一,并且小码哥知道货物的种类和数目,小码哥想知道他至少需要花费多少体力来解决这个问题。(小码哥可以合并任意两堆货物)
格式
输入格式:
输入包括两行,第一行是一个整数n,表示货物的种类数。
第二行包含n个整数,用空格分隔,第i个整数α是第i种货物的数目。
.
输出格式:
输出包括一行,这一行只包含一个整数,也就是最小的体力耗费值。
样例1
输入:
3
1 2 3
.
输出: 9
备注:
其中: 1≤n ≤1e4,1 < ai≤2e4
(2)参考代码
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;
#define ll long long
#define N 110000
ll c[N] ;
struct op{
ll v;
}s[N];
priority_queue<op> q;
bool operator < (const op &a , const op &b){
return a.v > b.v ;
}
int main(){
ll n;
cin >> n;
ll ans = 0 ,all = 0;
for (int i = 1; i <= n; i++){
cin >> c[i] ;
op f ;
f.v = c[i] ;
q.push(f) ;
}
while (q.size() != 1){
op f = q.top();
q.pop();
op g = q.top() ;
q.pop();
ans = ans + f.v + g.v ;
op h ;
h.v = f.v + g.v ;
q.push(h) ;
}
cout << ans ;
return 0;
}
16. MT2141 合并石子
(1)题目描述
地上有n堆石子,你每次可以合并任意两堆,每一次合并的代价为两堆石子的数量差值的绝对值,问如何合并才能拥有最小代价
以上问题小码哥当然知道你会,但是小码哥今天心情不错,他为了奖励你,将每一堆石子的初始数量变为了1,但是n的范围将会到达10的15次,即1≤n ≤10的15次
格式
输入格式:
多组数据
第一行输入一个w,表示共w组数据
每一组数据输入一个n
.
输出格式:
对于每一组数据输出一行,一个数字
样例1
输入:
4
5
16
3
12
.
输出:
2
0
1
4
备注:
提示:1≤n≤10的15次
(2)参考代码
#include<iostream>
#include<queue>
#include<vector>
#include<algorithm>
typedef unsigned long long llu;
using namespace std;
int main(){
priority_queue<llu,vector<llu>,greater<llu> >x;
//创建一个升序排序的优先队列,将greater改为less变为降序排序
int i=0,n,a;
cin >> n ;
while(i<n){
cin >> a ;
x.push(a);
i++;
}
llu s=0,y;
i=0;
while(i<n-1)
{
y=x.top();
x.pop();
y+=x.top();
x.pop();
x.push(y);
s+=y;
i++;
}
cout << s << endl ;
}
17. MT2142 第k小函数值
(1)题目描述
小码哥有n个函数,他们都可以写成二次函数的形式,即A沈Z+B*2+C;
对于不同的a 的值这些函数都可以产生许多函数值,小码哥想知道在产生的函数值中第k 小的值是什么。a属于正整数即[1,+无穷];
格式
输入格式:
第一行输入两个正整数n 和k。
以下n 行每行三个整数,其中第i行的三个数分别位A,Bi和C。
将这n个函数所有可以生成的函数值按非严格升序排序后的第个元素。
题目保证A一定为正
数据保证函数值不会超过longlong的数据范围。
.
输出格式: 输出第k个数
样例1
输入:
3 10
4 5 3
3 4 5
1 7 1
.
输出: 54
备注:
1<n≤20,1 <k ≤10000,1 < A; ≤10000,B;≤10000,C:≤10000
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct Node{
int a,b,c;
}node[30];
ll w[1000010];
ll p[1000010];
int total;
ll calc(int a,int b,int c,int x){
return (ll)a*x*x + (ll)b*x+c;
}
int main( )
{
int n,k;
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++){
scanf("%d%d%d",&node[i].a,&node[i].b,&node[i].c);
}
int x = 1;
int ans = 0;
bool f = 0;
while(true){
if(total>=k){
if(f){
memcpy(p,w,sizeof(ll)*(k+1));
sort(w+1,w+1+total);
bool flag = 1;
for(int i=1;i<=k;i++) if(w[i]!=p[i]){
flag = 0;
break;
}
if(flag){
ans = w[k];
break;
}
}else{
f = 1;
}
}
for(int i=1;i<=n;i++){
w[++total] = calc(node[i].a,node[i].b,node[i].c,x);
}
x++;
}
cout<<ans<<endl;
return 0;
}
18. MT2143 大约
(1)题目描述
给你一个相邻数差不超过1的序列,求最长子串的长度,满足子串中的最大值减最小值也不超过1。
格式
输入格式: 一个正整数n,然后是长度为n的整数序列
.
输出格式: 一个正整数表示答案
样例1
输入:
5
1 2 3 3 2
.
输出: 4
备注:
n≤100000,a[i]<=100000
(2)参考代码
#include<bits/stdc++.h>
#define oo 0x3f3f3f3f
#define OO 0x3f3f3f3f3f3f3f3f
#define LL long long
#define all(x) x.begin(),x.end()
#define close()ios::sync_with_stdio(0),cin.tie(nullptr),cout.tie(nullptr)
using namespace std;
const int N=1e5;
int main(){
int n,ans=0;
cin>>n;
vector<int> a(n) , f(N+1) ;
for(auto &x:a) cin>>x;//建议的读入写法
f[a[0]]=f[a[0]-1]=ans=1;//初始化
for(int i=1;i<n;++i){//主要部分
if(a[i-1]!=a[i]){
if(a[i-1]!=a[i]-1) f[a[i]-1]=0;
if(a[i-1]!=a[i]+1) f[a[i]]=0;
}
f[a[i]]+=1,f[a[i]-1]+=1;
ans=max(ans,max(f[a[i]],f[a[i]-1]));
}
cout<<ans<<'\n';
return 0;
}
19. MT2144 事务处理
(1)题目描述
小码哥被派去处理事情了,他有n个事情需要处理,每个事情有编号a,到来的时间t,需要占用的时间f,优先级vi ;
其中优先级用自然数表示,数字越大,则优先级越高。
如果一个事情到达的时候小码哥是空闲的,那么小码哥会一直做,直到做完这件事,除非在这个过程中,有一个比它优先级高的事情要干。在这种情况下,这个新的(优先级更高的)事情会被小码哥去处理,而老的只有等待。
如果一个进程到达时,小码哥正在处理一个比它优先级高或优先级相同的事情,则这个(新到达的)事情必须等待。一旦小码哥空闲,如果此时有事情在等待,则选择优先级最高的先处理。如果有多个优先级最高的事情,则选择到达时间最早的。
小码哥在第T秒收到了一个在所有待办事情中优先级最高的事情时,他最快只能在第T+1秒开始这个事情,无论小码哥在第T秒是否空闲。
格式
输入格式:
输入文件包含若干行,每一行有四个自然数(均不超过108) ,分别是编号ai,到达时间ti,执行时间f和优先级vi。不同事情有不同的编号,不会有两个相同优先级的事情同时到达。
输入数据已经按到达时间从小到大排序。输入数据保证在任何时候,等待队列中的进程不超过15000个。
.
输出格式: 按照事情结束的时间输出每个事情的进程号和结束时间
样例1
输入:
1 1 5 3
2 10 5 1
3 12 7 2
4 20 2 3
5 21 9 4
6 22 2 4
7 23 5 2
8 24 2 4
.
输出:
1 6
3 19
5 30
6 32
8 34
4 35
7 40
2 42
备注:
其中: n≤15000
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
struct Process{
int ai,ti,fi,vi;
bool operator < (const Process &b) const{
if(vi!=b.vi){
return vi<b.vi;
}
else{
return ti>b.ti;
}
}
bool read(){
return (scanf("%d%d%d%d",&ai,&ti,&fi,&vi)!=EOF);
}
}now,tp;
priority_queue<Process>q;
int main(){
int time,x;
while(now.read()){
x=now.ti-time;
while(!q.empty()){
tp=q.top();
q.pop();
if(tp.fi<=x){
x-=tp.fi;
time+=tp.fi;
cout<<tp.ai<<" "<<time<<endl;
}
else{
tp.fi-=x;
q.push(tp);
break;
}
}
time+=x;
q.push(now);
}
while(!q.empty()){
tp=q.top();
q.pop();
time+=tp.fi;
cout<<tp.ai<<" "<<time<<endl;
}
return 0;
}
20. MT2145 前k小数
(1)题目描述
小码哥现在手上有两个长度为n的数列a,b,(1≤i,j<=n)通过a+ b,可以构造出n* n个数,求构造出的数中前k小的数。
格式
输入格式:
第一行2个数n, k ;
第二行n个数,表示数列a
第三行n个数,表示数列b
.
输出格式: 从小到大输出前k小的数
样例1
输入:
3 3
2 6 6
1 4 8
.
输出: 3 6 7
备注:
提示1≤n ≤1e4,1 ≤k ≤n* n ≤1e41 ≤a,bj≤ le6
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
const int maxSize = 10100;
int a[maxSize];
int b[maxSize];
struct Node{
int sum,b;
Node(int sum,int b):sum(sum),b(b){}
bool operator < (const Node &b) const{
return sum>b.sum;
}
};
priority_queue<Node>minList;
int main(){
int n,k;
cin>>n>>k;
for(int i=0;i<n;i++){
cin>>a[i];
}
for(int i=0;i<n;i++){
cin>>b[i];
}
sort(a,a+n);
sort(b,b+n);
for(int i=0;i<n;i++){
minList.push(Node(a[i]+b[0],0));
}
for(int i=0;i<k;i++){
Node node=minList.top();
minList.pop();
cout<<node.sum<<" ";
int tempB = node.b;
if(tempB+1<n){
minList.push(Node(node.sum-b[tempB]+b[tempB+1],tempB+1));
}
}
return 0;
}
21. MT2146 前k小数(进阶)
(1)题目描述
给你n个长度为m的已知数列,你一次可以从每个数列中选出一个元素,共n个数,将这n个数的和,放入a数组中,穷举所有的选数可能,并且都放入a数组中。
问a数列中前k小数是多少。
格式
输入格式:
输入n , m, k;
接下来n行,每一行m个数,空格分隔,一行表示一个数列,共n行。
.
输出格式: 从小到大输出前k小的数
样例1
输入:
2 2 2
1 2
1 2
.
输出: 2 3
备注:
提示1<n ≤200,1 ≤k ≤m ≤200
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
const int N = 4e5 + 5;
int rec[400][400], n, m, k;
vector<int> a;
vector<int> u, v;
int main( )
{
cin >> n >> m >> k;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &rec[i][j]);
}
}
for (int i = 1; i <= m; i++) u.push_back(rec[1][i]);
for (int i = 2; i <= n; i++) {
sort(rec[i] + 1, rec[i] + 1 + m);
for (int j = 1; j <= k; j++) v.push_back(rec[i][j]);
for (int x: u) {
for (int y: v) {
a.push_back(x + y);
}
}
sort(a.begin(), a.end());
while (u.size() != 0) u.pop_back();
while (v.size() != 0) v.pop_back();
for (int i = 0; i < k; i++) u.push_back(a[i]);
while (a.size() != 0) a.pop_back();
}
for (int i = 0; i < k; i++) {
printf("%d ", u[i]);
}
return 0;
}
22. MT2147 数列最大数
(1)题目描述
小码哥想知道一个数列里最大的数,但这个数列会不断添加元素,每次都要重新快排的话太慢了,请你用一种足够快的方法帮他实现以下三种操作:
1 x//将整数x加入到数列中
2//输出数列中最大的数
3//删除数列中最大的数
对了,数列一开始是空的。
格式
输入格式:
第一行输入一个整数n,表示操作个数。
接下来n行,每行输入一个操作,格式如题目描述中所示。
.
输出格式: 对于每个操作2,输出一行一个整数表示答案。
样例1
输入:
5
1 1
1 4
2
3
2
.
输出:
4
1
备注:
保证:对于100%的数据: 1≤n ≤1,000, 000, 在int类型范围内,数列为空时只进行操作1。
(2)参考代码
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int n;
int h[N], sz;
void sift_up(int k) {
while (k > 1 && h[k] > h[k / 2]) {
swap(h[k], h[k / 2]);
k /= 2;
}
}
void sift_down(int k) {
while (k * 2 <= sz) {
int t = k;
if (h[k * 2] > h[t]) t = k * 2;
if (k * 2 + 1 <= sz && h[k * 2 + 1] > h[t]) t = k * 2 + 1;
if (t == k) return;
swap(h[k], h[t]);
k = t;
}
}
void push(int x) {
h[++sz] = x;
sift_up(sz);
}
void pop() {
h[1] = h[sz--];
sift_down(1);
}
int main() {
scanf("%d", &n);
while (n--) {
int op, x;
scanf("%d", &op);
if (op == 1) {
scanf("%d", &x);
push(x);
} else if (op == 2) printf("%d\n", h[1]);
else pop();
}
}
23. MT2148 一样的虫子
(1)题目描述
有N只虫子,每只虫子有6条腿,每条腿都有长度。
这些虫子的腿长得很奇怪,如图所示:
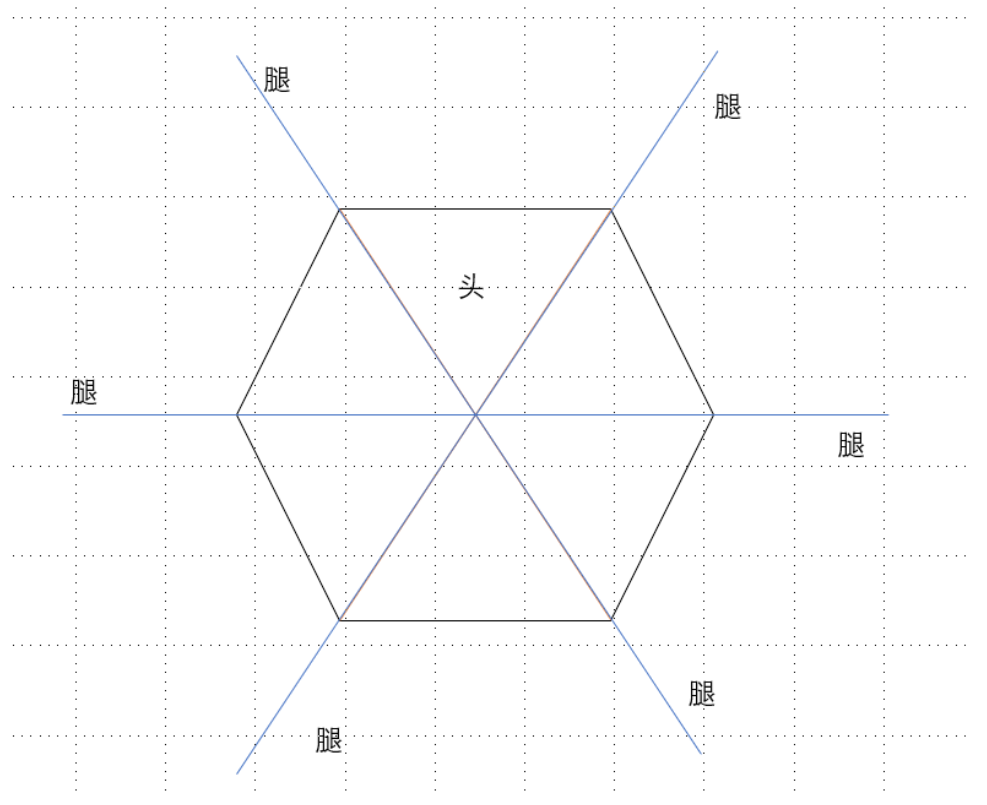

格式
输入格式:
输入的第一行将包含一个整数n,即要检查的虫子的数量。接下来是n行,每行描述一个虫子。每只虫子将由包含六个数
a1, a2, . . . , a6的行来描述,即虫子腿的长度。
.
输出格式:
如果所有的虫子都是不同的,你的程序应该打印消息:No
如果有两只虫子相同,你的程序应该打印消息:found.
样例1
输入:
2
1 2 3 4 5 6
4 3 2 1 6 5
.
输出: found.
备注:
其中:0<n ≤100000,0≤a1,… . , a6 ≤1000000
(2)参考代码
#include<algorithm>
#include<stdio.h>
#define ll unsigned long long
#define P 131
using namespace std;
ll ans[100001];
int t,n,a[7];
int main(){
scanf("%d",&n);
bool flag=false;
for(int i=1;i<=n;i++){
for(int j=1;j<=6;j++) scanf("%d",&a[j]);
ans[i]=0;
for(int k=1;k<=6;k++){
int k1=k+7,k2=k+7,o=6;
ll s1=0,s2=0;
while(o--){
if(k1%7==0) k1=1;
if(k2%7==0) k2=6;
s1=a[k1%7]+s1*P;
s2=a[k2%7]+s2*P;
k1++,k2--;
}
ans[i]=max(max(s1,s2),ans[i]);
}
}
sort(ans+1,ans+n+1);
for(int i=1;i<n;i++) if(ans[i]==ans[i+1]){
flag=true;
printf("found.\n");
break;
}
if(!flag) printf("No\n");
return 0;
}
24. MT2149 完美数对
(1)题目描述
定义完美数对:整数α和y,如果它们的差的绝对值等于k,即|c -引= k,那就称α和y是完美数对。
给定一个长度为n的整数数组α和一个整数k,请返回完美数对(ai, aj)的数目(i <j, (ai- a;= k)
格式
输入格式:
第一行两个整数n, k(1<=n<=105,1<= k<=104)
第二行有n个整数ai ( 1<= ai<=5* 104 )
.
输出格式: 一个整数,即完美数对的数目。
样例1:
输入:
4 1
1 2 2 1
.
输出:4
备注:
其中:1<=n<=10的5次, 1<=k<=10的4次 , 1<= ai<=5* 10的4次
(2)参考代码
#include<bits/stdc++.h>
using namespace std;
int nums[100005],counts[50005];
int n,k;
int count(){
for(int i=0;i<n;i++)
counts[nums[i]]++;
int res=0;
for(int i=1;i+k<50001;i++)
res+=counts[i]*counts[i+k];
return res;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++)
scanf("%d",&nums[i]);
printf("%d",count());
return 0;
}
25. MT2150 AB数对
(1)题目描述
题目是这样的:给出一串数以及一个数字C,要求计算出所有A-B=C的数对的个数
格式
输入格式:
输入共两行。
第一行,两个整数N,C (1<=N<=200000,1<=C<=30)。
第二行,N个整数(1~300),作为要求处理的那串数。
.
输出格式:一行,表示该串数中包含的满足A-B =C的数对的个数。
样例1
输入:
4 1
1 1 2 3
.
输出: 3
(2)参考代码
#include<bits/stdc++.h>
//2.AB数对
using namespace std;
int a[200200];
long long num[200100];
/*
思路:
我先记录所有数的出现次数
num[t] = m:代表数字 t 出现了 m次
之后有将b 从0-300遍历找出是否有符合的A = b+c
假设 num[5]=3 num[2]=2 c=3 那么符合条件的数对就有 3*2=6个
*/
int main( )
{
int n,c;
cin>>n>>c;
for(int i=0; i<n; i++){
int t;
cin>>t;
num[t]++;
}
long long ans=0;//注意用 long long ,int可能存不下 如 num[5]=100000 num[2]=100000 c=3 那么个数就有 10^10
for(int b=0; b<333; b++){
ans += num[b+c]*num[b];
}
cout<<ans<<endl;
return 0;
}
结语
感谢大家一直以来的不断支持与鼓励,码题集题库中的进阶塔350题正在逐步更新,之后会逐步跟进星耀,王者的题,尽请期待!!!
同时,也希望这些题能帮助到大家,一起进步,祝愿每一个算法道路上的“苦行僧”们,都能够历经磨难,终成正果,既然选择了这条路,走到了这里,中途放弃,岂不是太过可惜?
另附中国计算机学会的杰出会员、常务理事轩哥博士的B站视频讲解链接https://space.bilibili.com/518554541/?spm_id_from=333.999.0.0,供大家更好的进行学习与刷题~( ̄▽ ̄~)~
愿你的结局,配得上你一路的颠沛流离。




![[kerberos] kerberos 认证详解](https://img-blog.csdnimg.cn/095d22a62987493ea28bbf69f87b3d88.png)



![[DT框架使用教程01]如何在DT框架中创建插件](https://img-blog.csdnimg.cn/img_convert/63c663510ab76ce2d33768885e686f5d.png)