在 TensorFlow 2.0 及之后的版本中,默认采用 Eager Execution 的方式,不再使用 1.0 版本的 Session 创建会话。Eager Execution 使用更自然地方式组织代码,无需构建计算图,可以立即进行数学计算,简化了代码调试的过程。本文主要介绍 TensorFlow 的基本用法,通过构建一个简单损失函数,介绍 TensorFlow 优化损失函数的过程。
目录
1 tf.Tensor
2 tf.Variable
3 tf.GradientTape
TensorFlow 是一个用于机器学习的端到端平台。它支持以下内容:
- 基于多维数组的数值计算(类似于 NumPy)
- GPU 和分布式处理
- 自动微分
- 模型构建、训练和导出
1 tf.Tensor
TensorFlow 用 tf.Tensor 对象处理多维数组(或张量),以下是一个 2 维张量例子:
import tensorflow as tf
x = tf.constant([[1., 2., 3.],
[4., 5., 6.]])
print(x)tf.Tensor(
[[1. 2. 3.]
[4. 5. 6.]], shape=(2, 3), dtype=float32)
tf.Tensor 对象最重要的属性是 shape 与 dtype:
- Tensor.shape 返回张量每个维度的大小
- Tensor.dtype 返回张量中元素的数据类型
print(x.shape)(2, 3)
print(x.dtype)<dtype: 'float32'>
TensorFlow 实现了张量的标准数学运算,同时也包括为机器学习定制的运算。以下是一些示例:
x + x
5 * x
tf.transpose(x)
tf.nn.softmax(x, axis=-1)
tf.reduce_sum(x)2 tf.Variable
在 TensorFlow 中,模型的权重用 tf.Variable 对象存储,称为变量。
import tensorflow as tf
x = tf.Variable([0., 0., 0.])
x.assign([1, 2, 3])<tf.Variable 'UnreadVariable' shape=(3,) dtype=float32,
numpy=array([1., 2., 3.], dtype=float32)>
tf.Variable 对象的数值可以改变,在 TensorFlow 2.0 中,不再使用 Session 启动计算,变量可以直接算出结果。
x.assign_add([1, 1, 1,])<tf.Variable 'UnreadVariable' shape=(3,) dtype=float32,
numpy=array([2., 3., 4.], dtype=float32)>
x.assign_sub([1, 1, 1])<tf.Variable 'UnreadVariable' shape=(3,) dtype=float32,
numpy=array([1., 2., 3.], dtype=float32)>
3 tf.GradientTape
梯度下降法与相关算法是现在机器学习的基础。TensorFLow 实现了自动微分来计算梯度,通常用于计算机器学习模型的损失函数的梯度。
TensorFlow 2.0 提供了 tf.GradientTape 对象,可以理解为“梯度流”,顾名思义,tf.GradientTape 是用来计算梯度用的。
以下是一个简单的示例:
import tensorflow as tf
def f(x):
return x**2 + 2*x - 5
x = tf.Variable(1.0)
with tf.GradientTape() as tape:
y = f(x)
g_x = tape.gradient(y, x) # 计算 y 在 x = 1.0 处的梯度
print(g_x)4.0
最后,构建一个简单损失函数,并使用 TensorFlow 计算最小值。
import tensorflow as tf
def loss(x):
return x**2 - 10*x + 25
x = tf.Variable(1.0) # 随机初始值
losses = [] # 记录损失函数值
for i in range(100):
with tf.GradientTape() as tape:
one_loss = loss(x)
lossed.append(one_loss)
grad = tape.gradient(one_loss, x)
x.assign_sub(0.1 * grad) # 执行一次梯度下降法
print("The mininum of loss function is: ")
tf.print(x)The mininum of loss function is:
4.99999905
# 可视化优化过程
import matplotlib
from matplotlib import pyplot as plt
matplotlib.rcParams['figure.figsize'] = [8, 5]
plt.figure()
plt.plot(losses)
plt.title('Loss vs training iterations')
plt.xlabel('iterations')
plt.ylabel('loss')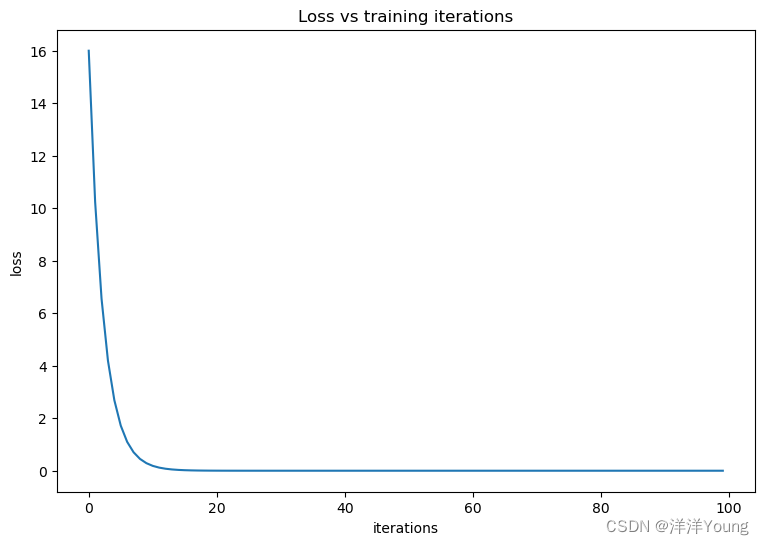








![[NOIP2007 普及组] 纪念品分组](https://img-blog.csdnimg.cn/4f8c98d0600d427aade5f3e49f2f4393.png)