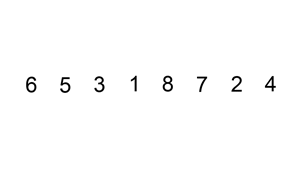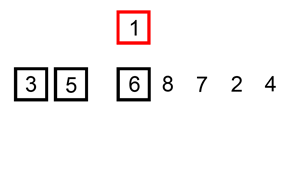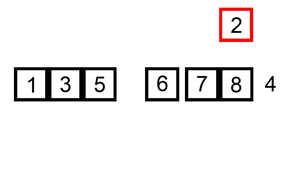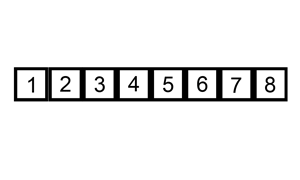文章目录
- 说明
- CNN卷积神经网络
- 1. 什么是CNN(CNN基础知识)
- 1. 基本概念
- 2.输入层
- 3.卷积层
- 3.1 图像
- 3.2 卷积核
- 3.3 偏置数
- 3.4 滑动窗口步长
- 3.5 特征图个数(特征图通道数或深度)
- 3.6 边缘填充
- 3.7 卷积过程例子
- 4. 激活函数
- 5. 池化层
- 6.全连接层
- 2. Day81 数据集读取与存储
- 2.1 Dataset 数据集
- 2.2 Size卷积尺寸类
- 2.3 枚举类(LayerTypeEnum)
- 3. Day82-83 数学操作
- 3.1 MathUtils 类各个方法理解
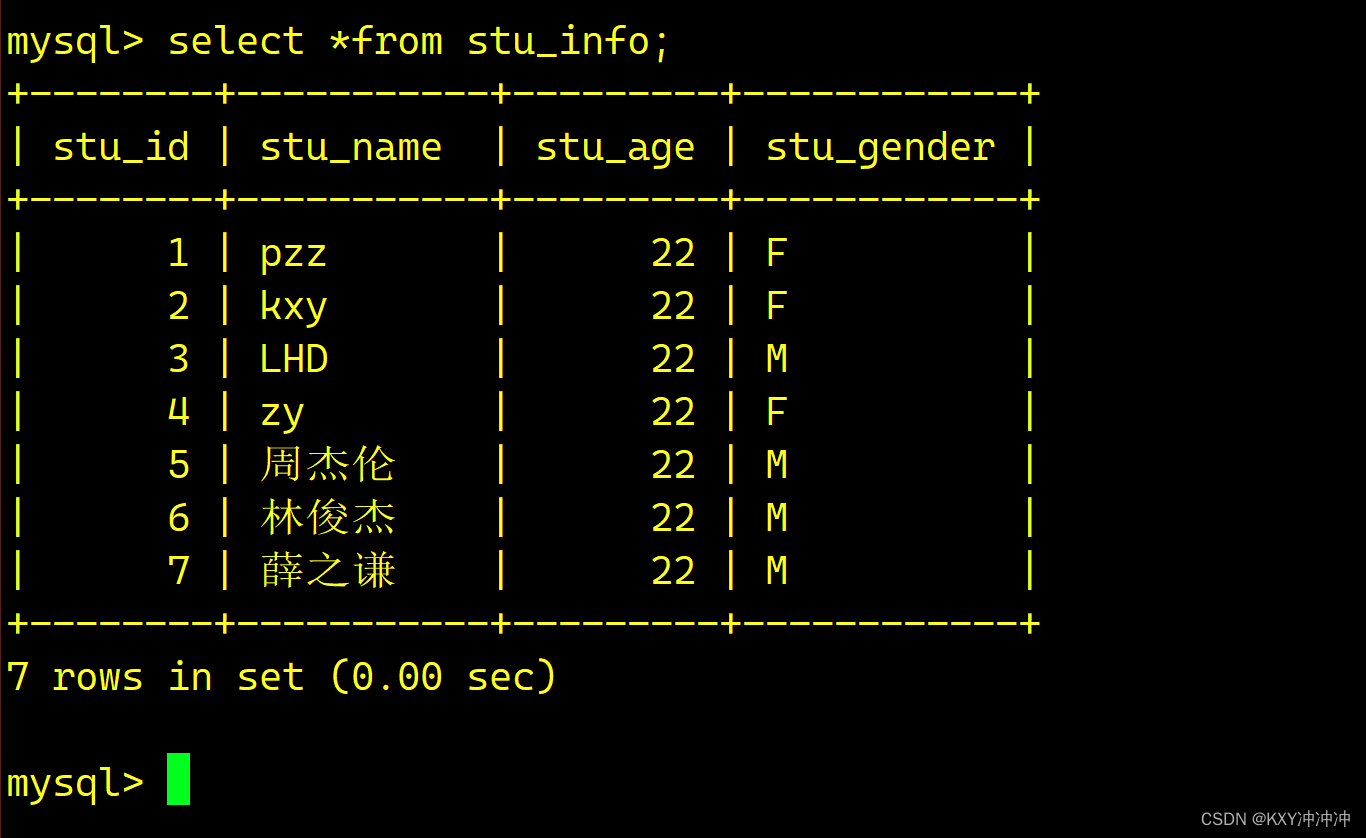
说明
闵老师的文章链接: 日撸 Java 三百行(总述)_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护:https://github.com/fulisha-ok/sampledata
CNN卷积神经网络
1. 什么是CNN(CNN基础知识)
1. 基本概念
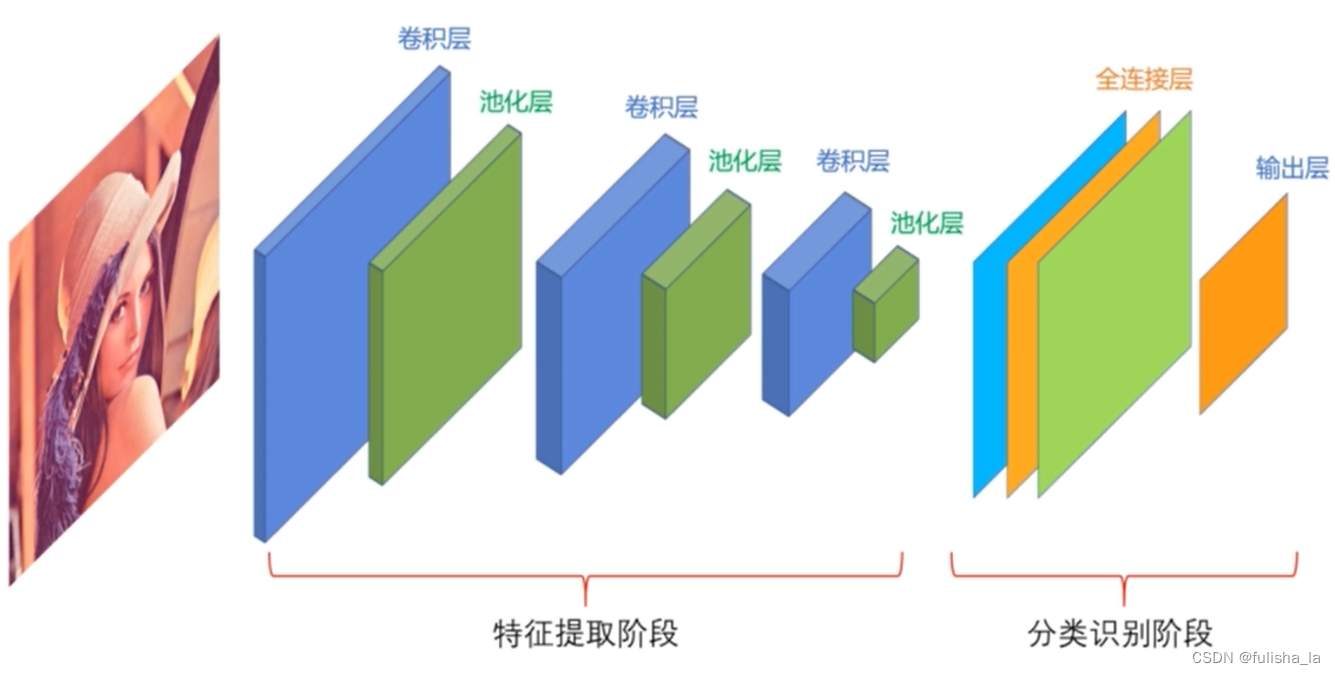
CNN(Convolutional Neural Network卷积神经网络),是一种深度学习算法,它的结构灵感来自人类视觉系统的工作方式。卷积神经网络的整体一个架构是:输入层–>卷积层–>激活函数–>池化层–>全连接层–>输出层
2.输入层
这是网络的输入,也就是原始图像数据。这个图像一般是三维数据(而我在之前学习的ANN它其实是一个向量数据)
3.卷积层
这一层是CNN的核心,它会包含多个卷积核(或滤波器)。卷积核通过在输入图像上进行卷积运算来提取特征,并生成对应的特征图。
3.1 图像
- 灰度图像:简单的理解就是灰度图像只有一个颜色通道
- 彩色图像:简单的理解就是彩色图像包含红、绿、蓝(RGB)三个颜色通道的信息

3.2 卷积核
对于灰度图像而言他的卷积核主要就是一个小的二维矩阵;对于彩色图形而言(简单的理解就是彩色图像包含红、绿、蓝(RGB)三个颜色通道的信息)他的卷积核主要就是一个小的三维张量。如下是一个彩色图像卷积核举例:
红色通道:
[
100
150
200
50
75
100
25
30
40
]
\left[\begin {array}{c} 100 & 150 & 200 \\ 50 & 75 & 100 \\ 25 & 30 & 40 \\ \end{array}\right]
1005025150753020010040
绿色通道:
[
200
180
160
140
120
100
80
60
40
]
\left[\begin {array}{c} 200 & 180 & 160 \\ 140 & 120& 100 \\ 80 & 60 & 40 \\ \end{array}\right]
200140801801206016010040
蓝色通道:
[
30
60
90
120
150
180
210
240
255
]
\left[\begin {array}{c} 30 & 60 & 90 \\ 120 & 150 & 180 \\ 210 & 240 & 255 \\ \end{array}\right]
301202106015024090180255
彩色图像的每个通道都是一个 3x3 的矩阵,表示图像在每个像素位置的对应颜色强度。我们把这三个通道的信息合并起来,就得到了一个三维张量,形状为 (3, 3, 3)。并列的样子如图下所示(这里只是举例,而不是如下图所示)
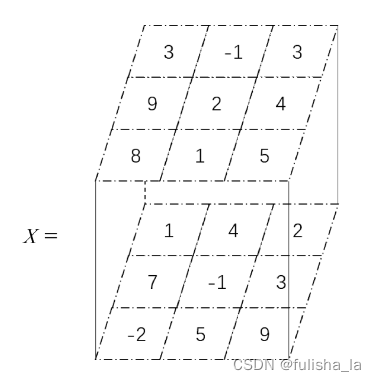
3.3 偏置数
每个卷积核都可以设置相应的偏置项。在ANN中正向传播函数中也回设置偏置参数。设置偏置参数目的就是为了更好的捕捉图像的特征。
3.4 滑动窗口步长
卷积核在输入数据上滑动的步长,它决定了输出特征图的尺寸
如下是步长为1的卷积:
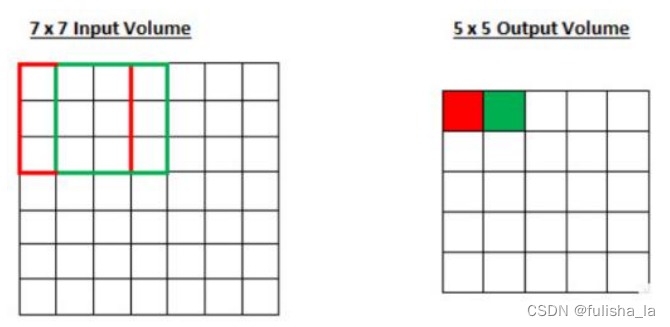
如下是步长为2的卷积:
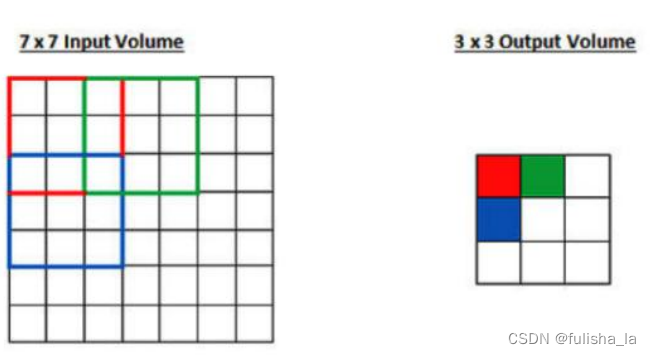
3.5 特征图个数(特征图通道数或深度)
特征图个数是由卷积层中使用的卷积核数量决定的。一个卷积层中使用了N个卷积核,那么这个卷积层就会生成N个输出特征图
如下图输入图像经过卷积层最后生成了6个特征图。
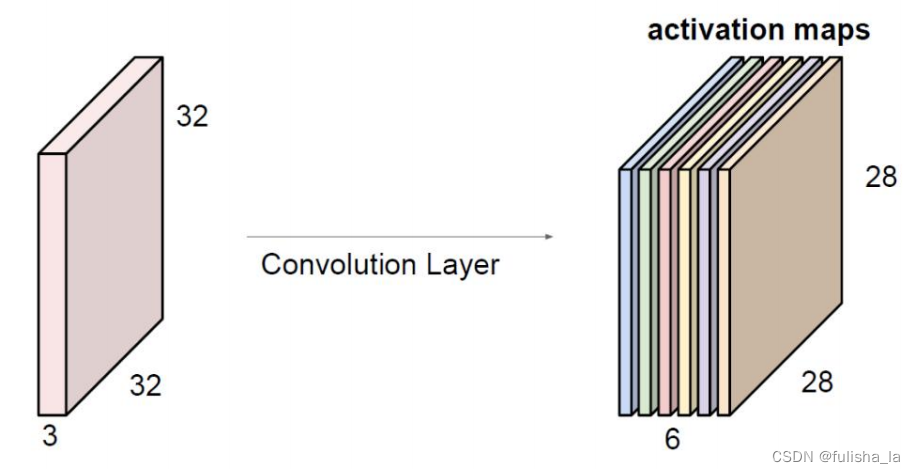
3.6 边缘填充
在进行卷积时,在输入数据的边界上添加额外的元素(一般是0,因为对原始数据基本没啥影响),以改变输出特征图的尺寸.一般边界的利用次数比较少,所以为了提高利用次数 就在外面加了一圈0,目的就是为了弥补边界缺失的信息。如下原始输入数据是5&5 但实际上矩阵的边界例如较少,所以在周围加上0就可以更好的通过原始数据捕捉特征。
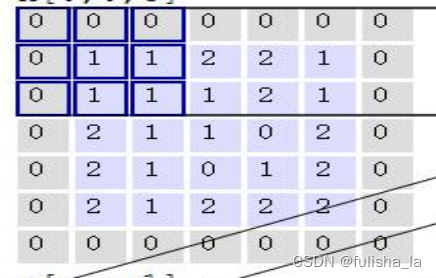
3.7 卷积过程例子
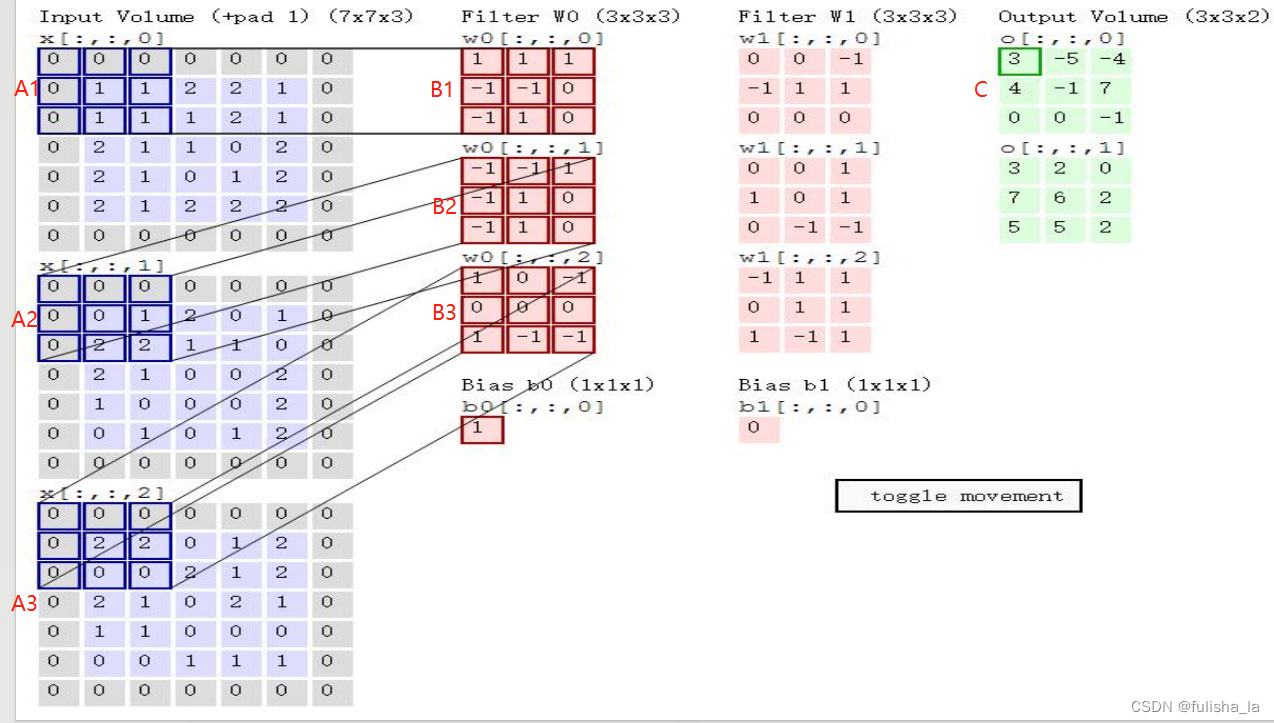
- 输入的数据( h e i g h t ∗ w i d t h ∗ d e p t h i m a g e , 如下三维图所示 height*width*depth image,如下三维图所示 height∗width∗depthimage,如下三维图所示)为 7 ∗ 7 ∗ 3 7*7*3 7∗7∗3: 其中图形是进行了边缘填充,输入的数据是一个二维图像 7 ∗ 7 7*7 7∗7,其中的depth=3代表图形的通道数
- 第一个卷积核为 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3:也和输入数据一样是一个三维张量,具有高度、宽度和深度维度
- 偏置数b0=1
- A1的 3 ∗ 3 3*3 3∗3矩阵 和卷积核B1 进行内积运算得值为:0;A2的 3 ∗ 3 3*3 3∗3矩阵 和卷积核B2 进行内积运算得值为:2; A3的 3 ∗ 3 3*3 3∗3矩阵 和卷积核B3 进行内积运算得值为:0;将三个相加0+2+0=2,再加上偏置1 即最后卷积的值为3,即C矩阵的第一个数。其他的计算都类似一样。矩阵移动步长为1
- 在图中可以知道,用了2个卷积核最后也会有2个特征图、
4. 激活函数
文章链接
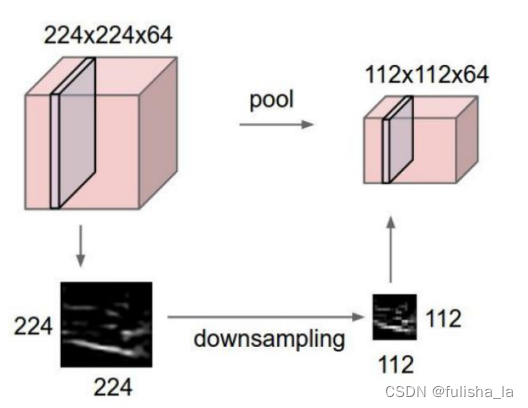
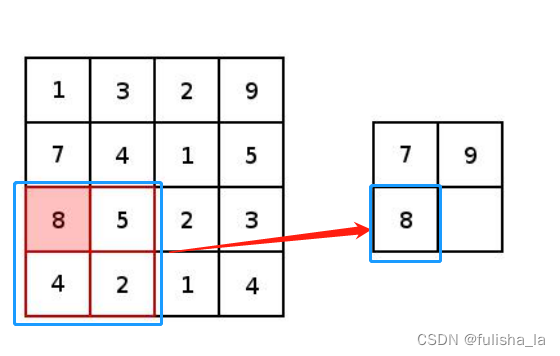
5. 池化层
对卷积后的特征图进行像下采样,以减小特征图的尺寸并保留重要的特征信息。类型有最大池化和平均池化。最大池化就是在窗口内选择最大的数值作为输出;平均池化就是在窗口内计算数值的平均值作为输出
6.全连接层
卷积层和池化层用于提取输入数据的局部特征;而全连接层将所有的特征数据映射到最终的输出类别上,用于分类、回归或其他任务。
2. Day81 数据集读取与存储
2.1 Dataset 数据集
这个是一个简单的数据集类,可用于表示和管理数据集中的数据实例。它通过读取文件中的数据并转换为 Instance 对象来初始化数据集。每个 Instance 对象包含属性数组和一个可选的标签值.
package machinelearing.cnn;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* @author: fulisha
* @date: 2023/7/29 13:47
* @description:
*/
public class Dataset {
/**
* All instances organized by a list.
*/
private List<Instance> instances;
/**
* The label index.
*/
private int labelIndex;
/**
* The max label (label start from 0).
*/
private double maxLabel = -1;
/**
* The first constructor.
*/
public Dataset() {
labelIndex = -1;
instances = new ArrayList<Instance>();
}
/**
* The second constructor.
* @param paraFilename The filename.
* @param paraSplitSign Often comma.
* @param paraLabelIndex Often the last column.
*/
public Dataset(String paraFilename, String paraSplitSign, int paraLabelIndex) {
instances = new ArrayList<Instance>();
labelIndex = paraLabelIndex;
File tempFile = new File(paraFilename);
try {
BufferedReader tempReader = new BufferedReader(new FileReader(tempFile));
String tempLine;
while ((tempLine = tempReader.readLine()) != null) {
String[] tempDatum = tempLine.split(paraSplitSign);
if (tempDatum.length == 0) {
continue;
} // Of if
double[] tempData = new double[tempDatum.length];
for (int i = 0; i < tempDatum.length; i++) {
tempData[i] = Double.parseDouble(tempDatum[i]);
}
Instance tempInstance = new Instance(tempData);
append(tempInstance);
} // Of while
tempReader.close();
} catch (IOException e) {
e.printStackTrace();
System.out.println("Unable to load " + paraFilename);
System.exit(0);
}//Of try
}// Of the second constructor
/**
* Append an instance.
* @param paraInstance The given record.
*/
public void append(Instance paraInstance) {
instances.add(paraInstance);
}
/**
* Append an instance specified by double values.
*/
public void append(double[] paraAttributes, Double paraLabel) {
instances.add(new Instance(paraAttributes, paraLabel));
}
/**
* Getter.
*/
public Instance getInstance(int paraIndex) {
return instances.get(paraIndex);
}
/**
* Getter.
*/
public int size() {
return instances.size();
}
/**
* Getter.
*/
public double[] getAttributes(int paraIndex) {
return instances.get(paraIndex).getAttributes();
}
/**
* Getter.
*/
public Double getLabel(int paraIndex) {
return instances.get(paraIndex).getLabel();
}
/**
* Unit test.
*/
public static void main(String args[]) {
Dataset tempData = new Dataset("D:/sampledata/sampledata/src/data/train.format", ",", 784);
Instance tempInstance = tempData.getInstance(0);
System.out.println("The first instance is: " + tempInstance);
}
/**
* An instance.
*/
public class Instance {
/**
* Conditional attributes.
*/
private double[] attributes;
/**
* Label.
*/
private Double label;
/**
* The first constructor.
*/
private Instance(double[] paraAttrs, Double paraLabel) {
attributes = paraAttrs;
label = paraLabel;
}
/**
* The second constructor.
*/
public Instance(double[] paraData) {
if (labelIndex == -1)
{
// No label
attributes = paraData;
} else {
label = paraData[labelIndex];
if (label > maxLabel) {
// It is a new label
maxLabel = label;
}
if (labelIndex == 0) {
// The first column is the label
attributes = Arrays.copyOfRange(paraData, 1, paraData.length);
} else {
// The last column is the label
attributes = Arrays.copyOfRange(paraData, 0, paraData.length - 1);
}
}
}
public double[] getAttributes() {
return attributes;
}
public Double getLabel() {
if (labelIndex == -1) {
return null;
}
return label;
}
public String toString(){
return Arrays.toString(attributes) + ", " + label;
}
}
}
输出结果:
The first instance is: [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], 0.0
- Instance 是 Dataset 类的内部类,表示数据集中的单个数据实例
- private List instances; 用于存储数据集中的所有数据实例
- labelIndex 表示标签在数据实例属性数组中的索引位置。如果为 -1,则表示数据实例没有标签
- maxLabel 记录数据集中出现的最大标签值
- tempReader.readLine() 读一行数据
- String 类的 split() 方法: 将字符串按照指定的分隔符拆分成一个字符串数组
2.2 Size卷积尺寸类
package machinelearing.cnn;
/**
* @author: fulisha
* @date: 2023/7/29 16:00
* @description:
*/
public class Size {
/**
* Cannot be changed after initialization.
*/
public final int width;
/**
* Cannot be changed after initialization.
*/
public final int height;
/**
* The first constructor.
* @param paraWidth The given width.
* @param paraHeight The given height.
*/
public Size(int paraWidth, int paraHeight) {
width = paraWidth;
height = paraHeight;
}
/**
* Divide a scale with another one. For example (4, 12) / (2, 3) = (2, 4).
* @param paraScaleSize The given scale size.
* @return The new size.
*/
public Size divide(Size paraScaleSize) {
int resultWidth = width / paraScaleSize.width;
int resultHeight = height / paraScaleSize.height;
if (resultWidth * paraScaleSize.width != width
|| resultHeight * paraScaleSize.height != height) {
throw new RuntimeException("Unable to divide " + this + " with " + paraScaleSize);
}
return new Size(resultWidth, resultHeight);
}
/**
* Subtract a scale with another one, and add a value. For example (4, 12) -
* (2, 3) + 1 = (3, 10).
* @param paraScaleSize The given scale size.
* @param paraAppend The appended size to both dimensions.
* @return The new size.
*/
public Size subtract(Size paraScaleSize, int paraAppend) {
int resultWidth = width - paraScaleSize.width + paraAppend;
int resultHeight = height - paraScaleSize.height + paraAppend;
return new Size(resultWidth, resultHeight);
}
public String toString() {
String resultString = "(" + width + ", " + height + ")";
return resultString;
}
public static void main(String[] args) {
Size tempSize1 = new Size(4, 6);
Size tempSize2 = new Size(2, 2);
System.out.println("" + tempSize1 + " divide " + tempSize2 + " = " + tempSize1.divide(tempSize2));
System.out.printf("a");
try {
System.out.println(
"" + tempSize2 + " divide " + tempSize1 + " = " + tempSize2.divide(tempSize1));
} catch (Exception ee) {
System.out.println(ee);
}
System.out.println(
"" + tempSize1 + " - " + tempSize2 + " + 1 = " + tempSize1.subtract(tempSize2, 1));
}
}
- divide方法(相除)
该方法将当前对象的宽度和高度分别除以 paraScaleSize 对象的宽度和高度,得到 resultWidth 和 resultHeight。然后,验证计算后的宽高度是不是整数倍,若否抛出 RuntimeException 异常。反之返回。 - subtract (相减)
该方法将当前对象的宽度和高度分别减去 paraScaleSize 对象的宽度和高度,并在每个维度上添加 paraAppend 的值,得到 resultWidth 和 resultHeight,然后返回。
2.3 枚举类(LayerTypeEnum)
package machinelearing.cnn;
/**
* @author: fulisha
* @date: 2023/7/29 16:00
* @description:
*/
public enum LayerTypeEnum {
INPUT, CONVOLUTION, SAMPLING, OUTPUT;
}
3. Day82-83 数学操作
3.1 MathUtils 类各个方法理解
MathUtils 类中定义了一系列数学操作和矩阵运算的静态方法
package machinelearing.cnn;
import java.io.Serializable;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Random;
import java.util.Set;
/**
* @author: fulisha
* @date: 2023/7/29 16:02
* @description:
*/
public class MathUtils {
/**
* An interface for different on-demand operators.
*/
public interface Operator extends Serializable {
public double process(double value);
}
/**
* The one-minus-the-value operator.
*/
public static final Operator one_value = new Operator() {
private static final long serialVersionUID = 3752139491940330714L;
public double process(double value) {
return 1 - value;
}
};
/**
* The sigmoid operator.
*/
public static final Operator sigmoid = new Operator() {
private static final long serialVersionUID = -1952718905019847589L;
public double process(double value) {
return 1 / (1 + Math.pow(Math.E, -value));
}
};
/**
* An interface for operations with two operators.
*/
interface OperatorOnTwo extends Serializable {
public double process(double a, double b);
}
/**
* Plus.
*/
public static final OperatorOnTwo plus = new OperatorOnTwo() {
private static final long serialVersionUID = -6298144029766839945L;
public double process(double a, double b) {
return a + b;
}
};
/**
* Multiply.
*/
public static OperatorOnTwo multiply = new OperatorOnTwo() {
private static final long serialVersionUID = -7053767821858820698L;
public double process(double a, double b) {
return a * b;
}
};
/**
* Minus.
*/
public static OperatorOnTwo minus = new OperatorOnTwo() {
private static final long serialVersionUID = 7346065545555093912L;
public double process(double a, double b) {
return a - b;
}
};
/**
* Print a matrix
*/
public static void printMatrix(double[][] matrix) {
for (int i = 0; i < matrix.length; i++) {
String line = Arrays.toString(matrix[i]);
line = line.replaceAll(", ", "\t");
System.out.println(line);
}
System.out.println();
}
/**
* Rotate the matrix 180 degrees.
*/
public static double[][] rot180(double[][] matrix) {
matrix = cloneMatrix(matrix);
int m = matrix.length;
int n = matrix[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n / 2; j++) {
double tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - 1 - j];
matrix[i][n - 1 - j] = tmp;
}
}
for (int j = 0; j < n; j++) {
for (int i = 0; i < m / 2; i++) {
double tmp = matrix[i][j];
matrix[i][j] = matrix[m - 1 - i][j];
matrix[m - 1 - i][j] = tmp;
}
}
return matrix;
}// Of rot180
private static Random myRandom = new Random(2);
/**
* Generate a random matrix with the given size. Each value takes value in
* [-0.005, 0.095].
*/
public static double[][] randomMatrix(int x, int y, boolean b) {
double[][] matrix = new double[x][y];
// int tag = 1;
for (int i = 0; i < x; i++) {
for (int j = 0; j < y; j++) {
matrix[i][j] = (myRandom.nextDouble() - 0.05) / 10;
}
}
return matrix;
}
/**
* Generate a random array with the given length. Each value takes value in
* [-0.005, 0.095].
*/
public static double[] randomArray(int len) {
double[] data = new double[len];
for (int i = 0; i < len; i++) {
//data[i] = myRandom.nextDouble() / 10 - 0.05;
data[i] = 0;
}
return data;
}
/**
* Generate a random perm with the batch size.
*/
public static int[] randomPerm(int size, int batchSize) {
Set<Integer> set = new HashSet<Integer>();
while (set.size() < batchSize) {
set.add(myRandom.nextInt(size));
}
int[] randPerm = new int[batchSize];
int i = 0;
for (Integer value : set) {
randPerm[i++] = value;
}
return randPerm;
}
/**
* Clone a matrix. Do not use it reference directly.
*/
public static double[][] cloneMatrix(final double[][] matrix) {
final int m = matrix.length;
int n = matrix[0].length;
final double[][] outMatrix = new double[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
outMatrix[i][j] = matrix[i][j];
}
}
return outMatrix;
}
/**
* Matrix operation with the given operator on single operand.
*/
public static double[][] matrixOp(final double[][] ma, Operator operator) {
final int m = ma.length;
int n = ma[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
ma[i][j] = operator.process(ma[i][j]);
} // Of for j
} // Of for i
return ma;
}// Of matrixOp
/**
* Matrix operation with the given operator on two operands.
*/
public static double[][] matrixOp(final double[][] ma, final double[][] mb,
final Operator operatorA, final Operator operatorB, OperatorOnTwo operator) {
final int m = ma.length;
int n = ma[0].length;
if (m != mb.length || n != mb[0].length) {
throw new RuntimeException("ma.length:" + ma.length + " mb.length:" + mb.length);
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
double a = ma[i][j];
if (operatorA != null) {
a = operatorA.process(a);
}
double b = mb[i][j];
if (operatorB != null) {
b = operatorB.process(b);
}
mb[i][j] = operator.process(a, b);
}
}
return mb;
}
/**
* Extend the matrix to a bigger one (a number of times).
*/
public static double[][] kronecker(final double[][] matrix, final Size scale) {
final int m = matrix.length;
int n = matrix[0].length;
final double[][] outMatrix = new double[m * scale.width][n * scale.height];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int ki = i * scale.width; ki < (i + 1) * scale.width; ki++) {
for (int kj = j * scale.height; kj < (j + 1) * scale.height; kj++) {
outMatrix[ki][kj] = matrix[i][j];
}
}
}
}
return outMatrix;
}
/**
* Scale the matrix.
*/
public static double[][] scaleMatrix(final double[][] matrix, final Size scale) {
int m = matrix.length;
int n = matrix[0].length;
final int sm = m / scale.width;
final int sn = n / scale.height;
final double[][] outMatrix = new double[sm][sn];
if (sm * scale.width != m || sn * scale.height != n) {
throw new RuntimeException("scale matrix");
}
final int size = scale.width * scale.height;
for (int i = 0; i < sm; i++) {
for (int j = 0; j < sn; j++) {
double sum = 0.0;
for (int si = i * scale.width; si < (i + 1) * scale.width; si++) {
for (int sj = j * scale.height; sj < (j + 1) * scale.height; sj++) {
sum += matrix[si][sj];
}
}
outMatrix[i][j] = sum / size;
}
}
return outMatrix;
}
/**
* Convolution full to obtain a bigger size. It is used in back-propagation.
*/
public static double[][] convnFull(double[][] matrix, final double[][] kernel) {
int m = matrix.length;
int n = matrix[0].length;
final int km = kernel.length;
final int kn = kernel[0].length;
final double[][] extendMatrix = new double[m + 2 * (km - 1)][n + 2 * (kn - 1)];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
extendMatrix[i + km - 1][j + kn - 1] = matrix[i][j];
}
}
return convnValid(extendMatrix, kernel);
}
/**
* Convolution operation, from a given matrix and a kernel, sliding and sum
* to obtain the result matrix. It is used in forward.
*/
public static double[][] convnValid(final double[][] matrix, double[][] kernel) {
// kernel = rot180(kernel);
int m = matrix.length;
int n = matrix[0].length;
final int km = kernel.length;
final int kn = kernel[0].length;
int kns = n - kn + 1;
final int kms = m - km + 1;
final double[][] outMatrix = new double[kms][kns];
for (int i = 0; i < kms; i++) {
for (int j = 0; j < kns; j++) {
double sum = 0.0;
for (int ki = 0; ki < km; ki++) {
for (int kj = 0; kj < kn; kj++) {
sum += matrix[i + ki][j + kj] * kernel[ki][kj];
}
}
outMatrix[i][j] = sum;
}
}
return outMatrix;
}
/**
* Convolution on a tensor.
*/
public static double[][] convnValid(final double[][][][] matrix, int mapNoX,
double[][][][] kernel, int mapNoY) {
int m = matrix.length;
int n = matrix[0][mapNoX].length;
int h = matrix[0][mapNoX][0].length;
int km = kernel.length;
int kn = kernel[0][mapNoY].length;
int kh = kernel[0][mapNoY][0].length;
int kms = m - km + 1;
int kns = n - kn + 1;
int khs = h - kh + 1;
if (matrix.length != kernel.length) {
throw new RuntimeException("length");
}
final double[][][] outMatrix = new double[kms][kns][khs];
for (int i = 0; i < kms; i++) {
for (int j = 0; j < kns; j++) {
for (int k = 0; k < khs; k++) {
double sum = 0.0;
for (int ki = 0; ki < km; ki++) {
for (int kj = 0; kj < kn; kj++) {
for (int kk = 0; kk < kh; kk++) {
sum += matrix[i + ki][mapNoX][j + kj][k + kk]
* kernel[ki][mapNoY][kj][kk];
}
}
}
outMatrix[i][j][k] = sum;
}
}
}
return outMatrix[0];
}
/**
* The sigmod operation.
*/
public static double sigmod(double x) {
return 1 / (1 + Math.pow(Math.E, -x));
}
/**
* Sum all values of a matrix.
*/
public static double sum(double[][] error) {
int m = error.length;
int n = error[0].length;
double sum = 0.0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sum += error[i][j];
}
}
return sum;
}
/**
* Ad hoc sum.
*/
public static double[][] sum(double[][][][] errors, int j) {
int m = errors[0][j].length;
int n = errors[0][j][0].length;
double[][] result = new double[m][n];
for (int mi = 0; mi < m; mi++) {
for (int nj = 0; nj < n; nj++) {
double sum = 0;
for (int i = 0; i < errors.length; i++)
sum += errors[i][j][mi][nj];
result[mi][nj] = sum;
}
}
return result;
}
/**
* Get the index of the maximal value for the final classification.
*/
public static int getMaxIndex(double[] out) {
double max = out[0];
int index = 0;
for (int i = 1; i < out.length; i++) {
if (out[i] > max) {
max = out[i];
index = i;
}
}
return index;
}
}
- Operator 接口
可以对单个值进行操作的操作符,接口中只有一个抽象方法 double process(double value) - one_value操作符
实现了 Operator 接口的匿名内部类,代表 “1 - value” 的操作符,它实现了 process 方法,用于返回 1 - value 的结果 - sigmoid操作符
实现了 Operator 接口的匿名内部类,代表 Sigmoid 函数的操作符,它实现了 process 方法,用于返回 Sigmoid 激活函数的结果 - OperatorOnTwo 接口
可以对两个值进行操作的操作符,接口中只有一个抽象方法 double process(double a, double b) - plus 操作符
实现了 OperatorOnTwo 接口的匿名内部类,代表加法操作符,它实现了 process 方法,用于返回 a + b 的结果 - multiply操作符
实现了 OperatorOnTwo 接口的匿名内部类,代表乘法操作符,它实现了 process 方法,用于返回 a * b 的结果 - minus 操作符
实现了 OperatorOnTwo 接口的匿名内部类,代表减法操作符,它实现了 process 方法,用于返回 a - b 的结果 - printMatrix(double[][] matrix)方法
打印一个二维矩阵 - rot180(double[][] matrix) 方法
将一个二维矩阵逆时针旋转180度 - randomMatrix(int x, int y, boolean b) 方法
生成一个指定大小的随机矩阵 - randomArray(int len)方法
生成一个指定长度的随机数组 - randomPerm(int size, int batchSize)方法
生成一个指定大小的随机排列(size 是排列的范围,batchSize 是排列的大小) - cloneMatrix方法
克隆矩阵 - matrixOp(final double[][] ma, Operator operator)方法
对单个操作数执行矩阵操作。matrixOp方法用于对输入矩阵ma中的每个元素应用给定的operator运算符,并返回执行后的结果 - matrixOp(final double[][] ma, final double[][] mb, final Operator operatorA, final Operator operatorB, OperatorOnTwo operator)
对两个操作数执行矩阵操作。使用两个指定的operatorA和operatorB对两个矩阵的元素执行操作、 - kronecker(final double[][] matrix, final Size scale)
扩展矩阵到更大的大小。对给定的矩阵 matrix 进行 Kronecker 乘积,并根据指定的 scale 尺寸进行缩放。
代码的一个举例过程:
m a t r i x = [ 1 2 3 4 ] matrix = \left[\begin {array}{c} 1 & 2 \\ 3 & 4 \\ \end{array}\right] matrix=[1324]
scale = Size(2, 3)
矩阵的大小: (4,6): m = 2 * 2 = 4,n = 2 * 3 = 6
matrix[0][0] = 1,对他进行填充:
[ 1 1 1 1 1 1 ] \left[\begin {array}{c} 1 & 1& 1 \\ 1 & 1& 1\\ \end{array}\right] [111111]
matrix[0][1] = 2 进行填充
[ 2 2 2 2 2 2 ] \left[\begin {array}{c} 2 & 2& 2 \\ 2 & 2& 2\\ \end{array}\right] [222222]
同理其他最后得到的矩阵:
[ 1 1 1 2 2 2 1 1 1 2 2 2 3 3 3 4 4 4 3 3 3 4 4 4 ] \left[\begin {array}{c} 1 & 1& 1 &2 & 2& 2 \\ 1 & 1& 1 &2 & 2& 2\\ 3 & 3& 3 &4 & 4& 4\\ 3 & 3& 3 &4 & 4& 4\\ \end{array}\right] 113311331133224422442244
kronecker积举例一个计算过程:
A矩阵:
[
a
11
a
12
a
21
a
22
]
\left[\begin {array}{c} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array}\right]
[a11a21a12a22]
B矩阵:
[
b
11
b
12
b
21
b
22
]
\left[\begin {array}{c} b_{11} & b_{12} \\ b_{21} & b_{22} \\ \end{array}\right]
[b11b21b12b22]
A
⊗
B
=
C
A ⊗ B=C
A⊗B=C的矩阵大小为 (m * p)x(n * q),其中m 和 n 是矩阵 A 的行数和列数,p 和 q 是矩阵 B 的行数和列数。故上面C矩阵是一个4x4的矩阵
其中
c
11
=
a
11
∗
B
=
[
a
11
∗
b
11
a
11
∗
b
12
a
11
∗
b
21
a
11
∗
b
22
]
c_{11}=a_{11}*B=\left[\begin {array}{c} a_{11}*b_{11}& a_{11}*b_{12} \\ a_{11}*b_{21} & a_{11}*b_{22} \\ \end{array}\right]
c11=a11∗B=[a11∗b11a11∗b21a11∗b12a11∗b22]
其中
c
12
=
a
12
∗
B
=
[
a
12
∗
b
11
a
12
∗
b
12
a
12
∗
b
21
a
12
∗
b
22
]
c_{12}=a_{12}*B=\left[\begin {array}{c} a_{12}*b_{11}& a_{12}*b_{12} \\ a_{12}*b_{21} & a_{12}*b_{22} \\ \end{array}\right]
c12=a12∗B=[a12∗b11a12∗b21a12∗b12a12∗b22]
以此类推,故最后的结果为:
C
=
[
a
11
∗
b
11
a
11
∗
b
12
a
12
∗
b
11
a
12
∗
b
12
a
11
∗
b
21
a
11
∗
b
22
a
12
∗
b
21
a
12
∗
b
22
a
21
∗
b
11
a
21
∗
b
12
a
22
∗
b
11
a
22
∗
b
12
a
21
∗
b
21
a
21
∗
b
22
a
22
∗
b
21
a
22
∗
b
22
]
C= \left[\begin {array}{c} a_{11}*b_{11}& a_{11}*b_{12} & a_{12}*b_{11}& a_{12}*b_{12} \\ a_{11}*b_{21} & a_{11}*b_{22} & a_{12}*b_{21} & a_{12}*b_{22} \\ a_{21}*b_{11}& a_{21}*b_{12} & a_{22}*b_{11}& a_{22}*b_{12} \\ a_{21}*b_{21} & a_{21}*b_{22} & a_{22}*b_{21} & a_{2 2}*b_{22} \\ \end{array}\right]
C=
a11∗b11a11∗b21a21∗b11a21∗b21a11∗b12a11∗b22a21∗b12a21∗b22a12∗b11a12∗b21a22∗b11a22∗b21a12∗b12a12∗b22a22∗b12a22∗b22
-
scaleMatrix(final double[][] matrix, final Size scale)
用于缩放矩阵的方法,即将原始矩阵按照指定的大小比例进行缩放。将原始矩阵缩小到一个更小的尺寸,通过将相邻元素的值进行平均来得到新的缩放后的矩阵
例如:
m a t r i x = [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ] matrix = \left[\begin {array}{c} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \\ \end{array}\right] matrix= 15913261014371115481216
设置的size: Size scale = new Size(2, 2);
经过scaleMatrix方法后,输出的矩阵大小为(2,2);为:- 对于第一行第一列的元素:计算原始矩阵中小区域 {(0, 0), (0, 1), (1, 0), (1, 1)} 内元素的平均值:(1 + 2 + 5 + 6) / 4 = 3.5,将其赋值给 scaledMatrix[0][0]。
- 最终的矩阵
[ 3.5 5.5 11.5 13.5 ] \left[\begin {array}{c} 3.5 & 5.5 \\ 11.5 & 13.5\\ \end{array}\right] [3.511.55.513.5]
-
convnFull(double[][] matrix, final double[][] kernel)
在原始矩阵的边缘进行零填充,再进行卷积操作。
举例:
原始矩阵matrix
m a t r i x = [ 1 2 3 4 5 6 7 8 9 10 11 12 ] matrix = \left[\begin {array}{c} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \\ \end{array}\right] matrix= 147102581136912
边缘进行零填充:
e x t e n d M a t r i x = [ 0 0 0 0 0 0 1 2 3 0 0 4 5 6 0 0 7 8 9 0 0 10 11 12 0 0 0 0 0 0 ] extendMatrix= \left[\begin {array}{c} 0 & 0 & 0 & 0& 0 & \\ 0 &1 & 2 & 3 & 0 \\ 0 & 4 & 5 & 6 & 0 \\ 0 & 7 & 8 & 9 & 0 \\ 0 & 10 & 11 & 12 & 0 \\ 0 & 0 & 0 & 0& 0 & \\ \end{array}\right] extendMatrix= 000000014710002581100369120000000
再调用convnValid进行卷积操作:
k e r n e l (卷积核) = [ 0 1 2 3 ] kernel(卷积核)= \left[\begin {array}{c} 0& 1 \\ 2 & 3 \\ \end{array}\right] kernel(卷积核)=[0213]
最后的结果为(内积):
o u t M a t r i x = [ 3 8 13 6 13 25 31 12 25 43 49 18 7 8 9 0 ] outMatrix= \left[\begin {array}{c} 3 & 8 & 13 & 6 \\ 13 & 25 & 31 & 12 \\ 25 & 43 & 49 & 18 \\ 7 & 8 & 9 & 0 \\ \end{array}\right] outMatrix= 3132578254381331499612180 -
convnValid(final double[][] matrix, double[][] kernel)
在二维矩阵matrix上进行卷积操作,卷积核为kernel,因此输出的矩阵大小会缩小。 -
convnValid(final double[][][][] matrix, int mapNoX,double[][][][] kernel, int mapNoY)
用于在四维张量上进行卷积操作,在这里,四维张量类似于多个特征图(Feature Map)的集合,这些特征图通常用于卷积神经网络中的不同层。

-
sum(double[][] error)
用于计算二维矩阵中所有元素的总和 -
sum(double[][][][] errors, int j)
这个方法通常用于在卷积层后、激活函数或池化层后,对多个特征图进行逐位置的求和操作,以得到更加丰富的特征表示。errors是一个四维数组,表示包含多个特征图(Feature Map)的集合(第一维表示特征图的深度或数量,第二维表示特征图的索引,第三维和第四维表示特征图的行和列) -
getMaxIndex
用于从给定数组中找到最大值,并返回最大值的索引位置