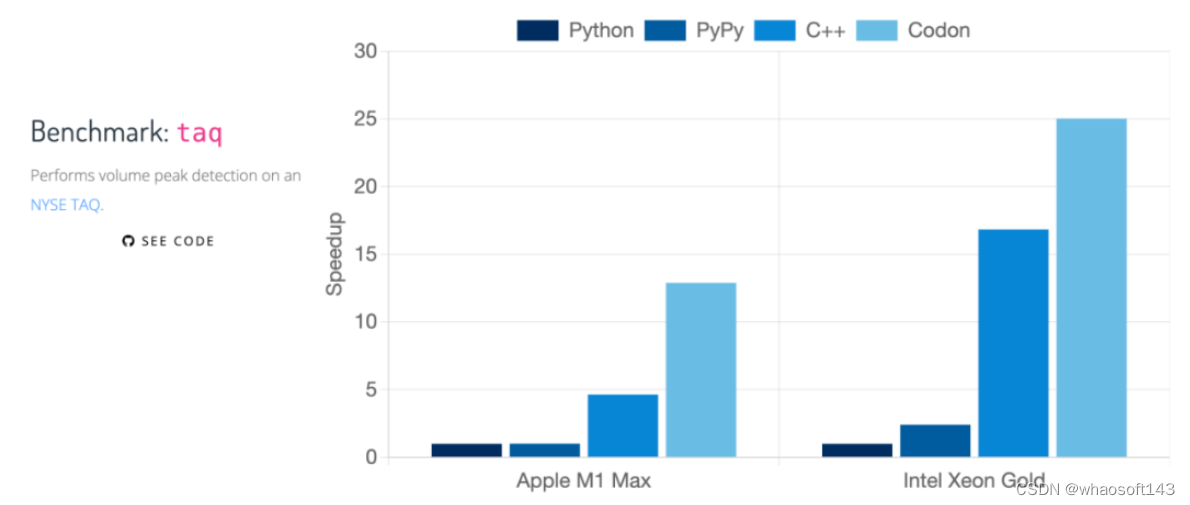
Python 已经成为世界上最流行的编程语言，尤其在深度学习、数据科学等领域占据主导地位。但是由于其解释执行的属性，Python 较低的性能很影响它在计算密集（比如多重 for 循环）的场景下发挥作用，实在让人又爱又恨。如果你是一名经常需要使用 Python 进行密集计算的开发者，我相信你肯定会有下面的类似经历：

• 我的 Python 程序里面有个很大的 for 循环，循环体里面全是密集的计算，跑起来好慢啊...

• 我的程序里面只有一小部分计算是性能瓶颈，虽然可以用 C++ 改写然后用 ctypes 绑定一下，但是那样会很麻烦，还会有在别的机器上编译不了的风险。我希望所有的工作都能在一个 Python 脚本中完成！

• 我之前是忠实的 C++/Fortran 用户，但是最近周围的同学用 Python 的越来越多，我也想试试 Python，但是无奈很多祖传代码用 Python 改写以后就会慢 100 多倍，我接受不了...

• 我的工作中需要处理大量图片数据，而需要的图像处理功能 OpenCV 又不提供，只能自己手写两重 for 循环，在 Python 里面这么搞真是太痛苦了 ...

如果你有类似的烦恼，那真的值得了解一下 Taichi。我来简单介绍一下：Taichi 是一个嵌入在 Python 中的领域特定语言，其一大功能就是加速 Python。Taichi 通过自己的编译器将被 @ti.kernel 修饰的函数编译到各种硬件上，包括 CPU 和 GPU，然后高性能执行。

（用户不用关心的）Taichi 运行原理：Python 代码被 Taichi 编译器编译到高性能二进制

由于 Taichi 开发者社区花了大量的精力优化 Taichi 在 Python 中的使用体验，所有的 Taichi 功能都可以在 import taichi as ti 以后使用，Taichi 本身也可以使用 pip 进行安装。当然，Taichi 也可以与常用的 Python 包（numpy、matplotlib、PyTorch 等）进行交互。

在这篇文章中，我们将通过三个计算例子来演示如何使用 Taichi 让你的 Python 轻松加速 > 50 倍。这三个例子是：1. 计算质数数目；2. 动态规划求解最长公共子序列；3. 求解反应-扩散方程。

🔗 https://github.com/taichi-dev/faster-python-with-taichi

计算素数个数

作为开胃小菜，我们先做一个小实验：计算小于给定正整数  的素数的个数。相信任何对 Python 有基础了解的人都不难写出类似下面这样的解法：

"""Count the number of primes in range [1, n].
"""

def is_prime(n: int):
    result = True
    for k in range(2, int(n ** 0.5) + 1):
        if n % k == 0:
            result = False
            break
    return result

def count_primes(n: int) -> int:
    count = 0
    for k in range(2, n):
        if is_prime(k):
            count += 1

    return count

print(count_primes(1000000))

这个方法的思路简单且粗暴：我们用一个函数 is_prime 来判断某个正整数  是不是素数，是素数则返回 1，不是则返回 0。这只要遍历检查从 2 到  之间是否有整数能够整除  即可。然后将小于  的全部整数依次代入此函数并统计结果。将上面的代码保存为 count_primes.py，在命令行运行：

time python count_primes.py

在我的电脑上输出的运行结果是：

78498

real        0m2.235s
user        0m2.235s
sys        0m0.000s

耗时 2.235 秒。也许代码中  设置成一百万对你的电脑来说太轻松了，要不要把  改成一千万试试？我打赌不管你的电脑多么高端，你起码都要等个半分钟才能看到结果。

好了下面是魔法时刻：我们不修改上面的函数体，只 import 一个“库”，然后给两个函数分别加一个装饰器：

"""Count the number of primes below a given bound.
"""
import taichi as ti
ti.init()

@ti.func
def is_prime(n: int):
    result = True
    for k in range(2, int(n ** 0.5) + 1):
        if n % k == 0:
            result = False
            break
    return result

@ti.kernel
def count_primes(n: int) -> int:
    count = 0
    for k in range(2, n):
        if is_prime(k):
            count += 1

    return count

print(count_primes(1000000))

仍然运行 time python count_primes.py 命令，输出的结果是：

78498

real        0m0.363s
user        0m0.546s
sys        0m0.179s

速度直接 x6! 而将  改成一千万的话，Taichi 的耗时只会增加到 0.8s 左右，而 Python 则需要大约 55 秒，Taichi 直接加速了 70 倍！不仅如此，我们还可以在 ti.init 中加上 ti.init(arch=ti.gpu) 参数，指定 Taichi 使用 GPU 来进行计算。在 GPU 上同样的计算 Taichi 只花了不到 0.45 秒，比 Python 足足快了 120 倍！你可以运行这里的代码亲身体会一下。

上面这个计算素数的例子使用的方法有点土，作为习题还可以，但在实际生产中就显得不那么实用了。我们接下来看一个实际中普遍使用的算法。

动态规划

动态规划（Dynamic Programming）是一类特别实用的算法，这类算法的哲学是以空间换时间，通过存储中间计算结果来减少重复计算量。我们这里选择一个求解最长公共子序列（Longest common subsequence, LCS）的例子 (算法导论的读者有木有)。

插播两个来自渊鸣的《算法导论》小故事：

1. 笔者小时候买过一本《算法导论》，书中提到四位作者都来自“麻雀理工学院”。当时还很好奇：怎么会有学校叫这么奇怪的名字... 过了一阵才意识到自己可能成了盗版书籍的受害者。

2. 10 年后，我还真的来到了麻省理工学院（MIT）读博士，一年后进行硕士论文答辩（MIT 叫做 Research Qualification Exam），我自然就带着 Taichi 的论文去了。答辩委员会里面有一位慈祥的教授，Charles E. Leiserson，嗯，就是《算法导论》的作者之一，“CLRS” 之中的 L。

言归正传。所谓子序列，就是一个序列的子集，但是保持它们在原序列中的顺序。比如说 [1, 2, 1] 是 [1, 2, 3, 1] 的子序列，而 [3, 2] 则不是。我们这里考虑对两条给定的序列，求出它们最长公共子序列的长度。最长公共子序列就是两个序列的所有公共子序列中最长的一条 (这个最长子序列未必唯一，但它的长度是唯一确定的)。

举个例子：

a = [0, 1, 0, 2, 4, 3, 1, 2, 1]

和

b = [4, 0, 1, 4, 5, 3, 1, 2]

的最长公共子序列是

LCS(a, b) = [0, 1, 4, 3, 1, 2]

最长公共子序列有很多应用。比如大家日常使用的 Linux diff 命令和 git 工具（比较两个文件之间的相似度），还有生物信息学中判断两段基因的相似度（把数字换成 ACGT 就行），其中的实现都用到了 LCS。

动态规划计算 LCS 的想法是我们依次求解序列 a 的前 i 个元素和序列 b 的前 j 个元素的最长公共子序列的长度，通过让 i 和 j 逐渐增加我们就逐步得出了最终的结果。我们用 f[i, j] 表示 LCS((prefix(a, i), prefix(b, j)，其中 prefix(a, i) 表示序列 a 的前 i 个元素，即 a[0], a[1], ..., a[i - 1]。这样我们就得到递推式：

f[i, j] = max(f[i - 1, j - 1] + (a[i - 1] == b[j - 1]),
              max(f[i - 1, j], f[i, j - 1]))

于是，一个 LCS 算法用 Python 可以很自然地书写为：

for i in range(1, len_a + 1):
    for j in range(1, len_b + 1):
        f[i, j] = max(f[i - 1, j - 1] + (a[i - 1] == b[j - 1]),
                      max(f[i - 1, j], f[i, j - 1]))

这里我们给出一个 Taichi 的加速实现：

import taichi as ti
import numpy as np

ti.init(arch=ti.cpu)

benchmark = True

N = 15000

f = ti.field(dtype=ti.i32, shape=(N + 1, N + 1))

if benchmark:
    a_numpy = np.random.randint(0, 100, N, dtype=np.int32)
    b_numpy = np.random.randint(0, 100, N, dtype=np.int32)
else:
    a_numpy = np.array([0, 1, 0, 2, 4, 3, 1, 2, 1], dtype=np.int32)
    b_numpy = np.array([4, 0, 1, 4, 5, 3, 1, 2], dtype=np.int32)


@ti.kernel
def compute_lcs(a: ti.types.ndarray(), b: ti.types.ndarray()) -> ti.i32:
    len_a, len_b = a.shape[0], b.shape[0]

    ti.loop_config(serialize=True) # 避免 Taichi 自动并行
    for i in range(1, len_a + 1):
        for j in range(1, len_b + 1):
            f[i, j] = max(f[i - 1, j - 1] + (a[i - 1] == b[j - 1]),
                          max(f[i - 1, j], f[i, j - 1]))

    return f[len_a, len_b]


print(compute_lcs(a_numpy, b_numpy))

将上面的代码保存为 lcs.py，然后在终端运行：

time python lcs.py

得到的结果为（具体结果每次未必一致）：

2721

real        0m1.409s
user        0m1.112s
sys        0m0.549s

我们在代码中同时提供了分别使用 Taichi 和 Numpy 计算的版本，在我的电脑上对两个长度是 N=15000 的随机序列进行计算 Taichi 版本大约需要 0.9 秒，而 Python 则需要 476s，足足差了 500 多倍！大家可以运行一下体会 Taichi 相对 Numpy 那种飞一样的感觉。

当然，Numpy 主要针对的场景是以数组为基本单位的运算，遇到这种需要在数组内更细粒度进行计算的情况就比较无力了。而这正是 Taichi 能够发挥作用的地方。

反应 - 扩散方程

在大自然中我们常常会在动植物的表面见到一些有趣的图案，比如斑马身上的条纹，猎豹身上的斑点，河豚表面的花纹等等。

这些图案看起来是不规则的，但是又有一定的规律，并不完全随机。从进化的观点，这些图案是生物在长期演进和自然选择中逐渐形成的，但到底是什么规则决定了它们的形状一直是个有趣的问题。阿兰 . 图灵 (正是图灵机的发明人) 是最早注意到这一现象并尝试给出模型描述的人。他在论文 "The Chemical Basis of Morphogenesis" 中提出可以用两种化学物质 U, V 之间的相互作用来模拟图案的形成过程，其中物质 U 的角色类似被捕食者 (prey)，物质 V 的角色类似捕食者 (predator)。它们之间的作用服从如下规则：

1. 初始时空间中随机地分布了一些 U, V。

2. 在每个时刻 1, 2, 3, ..., U, V 两种物质都向其邻域扩散。

3. 当 U, V 相遇时，一定比例的 U, V 会合并转化为更多的 V (捕食者在捕食后数量会增加)

4. 为了避免捕食者 V 的数量过多导致 U 的数量被消耗光，我们在每个时刻按照一定的比例 f 添加 U，同时按照一定的比例 k 移走 V。

于是整个过程可以用下面的反应 - 扩散方程描述：

这里关键的控制参数有四个，分别是 ， 分别控制 U, V 的扩散速度， 代表 feed，控制 U 的添加量，而  代表 kill，控制移走 V 的比例。

为了在 Taichi 中模拟这一过程，我们将空间划分为网格，每个网格中 U, V 的浓度值用一个 vec2 来表示。注意拉普拉斯算子  的数值计算是需要访问当前网格周围的网格的，为了避免一边修改一边读取这种操作的发生，我们需要开辟两个形状为  的网格，每次用其中一个网格的值作为旧值，将更新后的浓度值写入另一个网格中，然后交换两个网格的角色。所以我们需要的数据结构应该是：

W, H = 800, 600
uv = ti.Vector.field(2, float, shape=(2, W, H)) 

初始时，我们假定网格中 U 的浓度处处是 1，然后随机选择 50 个点撒上 V：

import numpy as np

uv_grid = np.zeros((2, W, H, 2), dtype=np.float32)
uv_grid[0, :, :, 0] = 1.0
rand_rows = np.random.choice(range(W), 50)
rand_cols = np.random.choice(range(H), 50)
uv_grid[0, rand_rows, rand_cols, 1] = 1.0
uv.from_numpy(uv_grid)

实际的计算代码非常之简短：

@ti.kernel
def compute(phase: int):
    for i, j in ti.ndrange(W, H):
        cen = uv[phase, i, j]
        lapl = uv[phase, i + 1, j] + uv[phase, i, j + 1] + uv[phase, i - 1, j] + uv[phase, i, j - 1] - 4.0 * cen
        du = Du * lapl[0] - cen[0] * cen[1] * cen[1] + feed * (1 - cen[0])
        dv = Dv * lapl[1] + cen[0] * cen[1] * cen[1] - (feed + kill) * cen[1]
        val = cen + 0.5 * tm.vec2(du, dv)
        uv[1 - phase, i, j] = val

这里我们使用了取值为 0 或 1 的整数 phase 来控制使用 uv 的哪一层来作为旧的网格，并将更新的值写入 1-phase 对应的层中。

根据 V 的浓度进行染色，我们得到了如下的动画效果:

，时长00:10

非常有趣的是，虽然 V 的初始浓度是随机设置的，但是最终得到的图案却具有相似性。

我们在代码中提供了基于 Taichi 和 Numba 的两份不同的实现，Taichi 的版本由于使用了 GPU 进行计算，计算的部分可以轻松达到 300+ fps，而 Numba 的版本计算部分虽然也是编译执行的，但由于是在 CPU 上计算的，只有大约 30fps 左右。大家可以亲自运行代码体会一下 Taichi 使用 GPU 加速的巨大优势。

总结

在这三个例子上 Taichi 都让程序有了大幅加速。主要的性能来自三点：

1. Taichi 是编译性的，而 Python 是解释性的

2. Taichi 能自动并行，而 Python 通常是单线程的

3. Taichi 能在 GPU 上运行，而 Python 本身是在 CPU 上运行的

当然，加速 Python 还有很多其他工具，这里我们分析一下他们和 Taichi 的优劣。

与 Numpy/JAX/PyTorch/TensorFlow 比较：这几类工具都高度基于数组运算。计算的最小单位是数组，在 Data Science、Deep Learning 等领域是有明显的优势的。但是在科学计算领域，这样做导致灵活性缺失：比如说前面那个计算质数的程序，就比较难使用数组运算表示出来。Taichi 的优势就在于其灵活性，能够直接操纵循环的每一次迭代，以一种更细颗粒度进行对于计算的描述，类似 C++ 和 CUDA。

与 Cython 比较：使用 Cython 编写程序实现加速也是一种常见的选择。在 Numpy 和 Scipy 的官方代码中有不少模块都是使用 Cython 编写然后编译的。但按照 Cython 的要求书写代码会比较麻烦，会牺牲一些可读性。Cython 支持一定程度的并行计算，但不支持直接调用 GPU 进行计算。

与 Numba 比较：Numba 顾名思义，是非常适合针对 Numpy 进行加速的方案。当你的函数是针对 Numpy 的数组向量化的操作时，使用 Numba 将其编译以后执行可以大大加速。Taichi 相比 Numba 的优势还有：1. Taichi 支持各种灵活的数据类型，比如 struct, dataclass, quant, sparse 等等，你可以任意指定它们的内存排布，当数据量庞大时这个优势会非常明显。而 Numba 只有在针对 Numpy 的稠密数组时效果最佳。2. Taichi 可以调用不同的 GPU 后端进行计算，所以写大规模并行程序（如粒子仿真、渲染器等）这种操作对 Taichi 来说是小菜一碟。但你很难想象可以用 Numba 写一个还过得去的 (哪怕离线) 渲染器。

与 Pypy 比较：Pypy 是一个 Python 的 JIT 编译器，这个工具 2007 年就有了，和 Taichi 的解决方案有些类似，都是通过编译的方式加速 Python。Pypy 最大优势在于 Python 代码完全不用改变，就能通过 Pypy 加速。但是这也是 Pypy 加速比率比 Taichi 低的原因：因为 Pypy 需要在编译的同时保持 Python 所有的语言特性，所以能够进行的优化比较有限。而 Taichi 有一套自己的语法，虽然和 Python 很像但是也有自己的一些假设，这使得 Taichi 能够实现更大的加速。

与 ctypes 比较：ctypes 可以让用户在 Python 中调用 C 函数。C++、CUDA 编写的程序也可以用过 C 接口暴露给 Python 使用。但是，ctypes 会让工具链复杂化：为了写一段比较快的程序，用户需要同时掌握 C、Python、CMake、CUDA 等等语言，和本文描述的完全在 Python 中解决问题的方案比起来还是麻烦了一些。

总而言之，在科学计算任务上，Taichi 还是有自己独特的优势的，大家可以根据自己的需求选择最合适的工具。如果你需要在 Python 中实现类似 C/C++ 语言的性能，Taichi 不失为一个理想的选择！

最后，我们希望 Taichi 能够为你带来价值，也希望能够听到你对 Taichi 的反馈，欢迎给我们提交 issues。如果想一键体验 Taichi，只需要执行👇🏻

pip install -U taichi

并执行👇🏻

ti gallery

就可以体验各种基于 Taichi 的高性能可视化 Demos，期待与大家相遇！