此前先后花了十元去做了乙级题，从最开始分别是70，35，43，33（途中做了RobpCom,只搞定了签到题），想着报今年的冬季赛，但是报名费有点高啊，加上做下来感觉不怎么样，后面在比赛结束后也是抽了3个小时去感受一下，满分是没想到的，不过可能因为考试环境比较轻松吧，下面为大家解析本人通关代码。

注：本人的方法或许不是最优，然后在做的过程也是比较烦心的，新题目，还得调整好心态，认真算下来两个小时不到就做完了，结束的时候还有半小时，当时反正是想要放弃的，觉得说也不难，就是实现不了，要么样例过了没全对，要么不知道错在哪，经此，心态真的很重要，原本才四五十分，搞着搞着就满分了

B-1 谣言检测仪

谣言有很多种，本题请你设计一种检测仪，专门针对一类吹牛话术进行验证。

有人喜欢吹牛，说自己做一场报告有 N 次掌声。现给定这个人的报告录音文字版，其中如果有掌声，记录中会出现 (zhangsheng) 字样。请你统计一下报告过程中到底出现了多少次掌声，并且与其说出的掌声次数做个比较，来判断这是不是谣言。

输入格式：

输入在第一行给出一个不超过 100 的正整数 N，即某人号称自己收获的掌声次数。

随后给出由英文字母、数字、标点符号（包括 ,、.、;、:、!）、空格、回车、以及 (zhangsheng) 组成的报告文本，为不超过 105 个字符的非空字符串，其中语音记录的文本以 # 结尾。

输出格式：

首先输出语音记录中真实的掌声次数。如果真实次数不小于 N，则随后空 1 格输出 True；否则输出 False。

输入样例 1：

3
Hello (zhangsheng).  Glad to meet everyone(zhangsheng).
See you (zhangsheng) next time.#

输出样例 1：

3 True

输入样例 2：

3
Hello (zhangsheng).  Glad to meet everyone(zhang
sheng). Let me hear your zhangsheng!
#

输出样例 2：

1 False

// 这道题就是字符串处理，15分的题没那么难，但是却是我提交最多的一个，注意细节吧，这里我犯了几个错误，第一最开始我用字符串的find函数去对"(zhangsheng)"作检测，然后统计，但是如果一个字符串里面有两个"(zhangsheng)"呢，毕竟，find函数只是判断存不存在，于是后面就用了比较笨的办法，直接挨个判断；第二题目是说真实次数不小于N，也就是大于或等于，而不是等于；第三在判断循环结束条件上，我此前是判断一条字符的最后一个是否是#，也就导致最后一分的样例始终没得到，最后想着再用find函数，有#我们就结束，然后就满分了

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,x=0;string s;
    cin>>n;
    getchar();
    while(cin>>s){
           if(s.find("#")!=-1)break;
        for(int i=0;i<s.size();i++)
if(s[i]=='('&&s[i+11]==')'&&s[i+5]=='g'&&s[i+1]=='z'&&s[i+2]=='h'&&s[i+3]=='a'&&s[i+4]=='n'&&s[i+6]=='s'&&s[i+7]=='h'&&s[i+8]=='e'&&s[i+9]=='n'&&s[i+10]=='g')
                x++;
    }
    if(x>=n)cout<<x<<" True";
    else cout<<x<<" False";
    return 0;
}

 

B-2 一道数学题

设整数 m 和 n 在给定闭区间 [a,b] 内，且满足等式 (n2−mn−m2)2=1。请你求出 m2+n2 的最大值。

输入格式：

输入给出两个正整数 a 和 b（1<a<b≤3×104），为闭区间的两个端点。

输出格式：

在一行中按照以下格式输出：

max( m^2 + n^2 ) = s

其中 s 是题面要求的 m2+n2 的最大值，m 和 n 分别对应能取到最大值的 m 和 n 的值。

输入样例：

10 100

输出样例：

max( 55^2 + 89^2 ) = 10946

//这道题真的就是数学题了，一次提交就过了，没啥好说的，就是根据题目，循环加判断 

#include<bits/stdc++.h>
using namespace std;
int main(){
    int a,b,i,j,k=0,x,y;
    cin>>a>>b;
    for(i=b;i>=a;i--){
       for(j=b;j>=a;j--){
           if((i*i-i*j-j*j)*(i*i-i*j-j*j)==1){k=1;x=i,y=j;break;}
       }
        if(k==1)break;
    }
    printf("max( %d^2 + %d^2 ) = %d",y,x,x*x+y*y);
    return 0;
}

 

 B-3 代号大本钟

在“一年一度喜剧大赛”上有一部作品《代号大本钟》，讲的是二战期间德国情报站里有一位英国间谍，代号“大本钟”。当最后情报站只剩下两个人的时候，站长坚信真正的间谍不是间谍，然后用了一下排除法，那就只有他自己是大本钟了……

现在假设情报站进行了 N 人次排查，最后请你用排除法来查一下，谁是那个“大本钟”？

输入格式：

输入第一行给出一个正整数 N（≤104）。随后 N 行，按照排查的时间先后顺序，每行给出一人次排查的结果，格式为：

代号 排查结果

其中 代号 是一个 4 位数字，为被排查的人的编号；排查结果 为 1 表示这人有间谍嫌疑，为 0 表示排除了这人的嫌疑。注意：同一个人可能被排查多次，但无论此前有多少次被列为嫌疑人，本次排查结果为 0 就排除了前面的所有怀疑。

输出格式：

根据排除法，在一行中列出所有被排查的人中有可能是“大本钟”的人的编号。编号按递增序给出，相邻编号间以 1 个空格分隔，行首尾不得有多余空格。

如果只有一个人有嫌疑，则在第二行输出 Da Ben Zhong is found!；如果有多个嫌疑，则输出 There are n suspects.，其中 n 是嫌疑人的个数。

题目保证至少有一个人是“大本钟”。

输入样例 1：

10
1234 1
2234 0
3234 1
1234 1
3234 1
2234 0
2234 1
3234 0
1234 0
1234 0

输出样例 1：

2234
Da Ben Zhong is found!

输入样例 2：

10
1234 1
2234 0
3234 1
1234 1
3234 1
2234 0
2234 1
3234 0
1234 0
1234 1

输出样例 2：

1234 2234
There are 2 suspects.

//这道题让我想起了帅到没朋友：题目详情 - L1-020 帅到没朋友 (pintia.cn)

题目比较简单，现在来看好像cmp函数有些多余了，也不用结构体，数组解决就可以，总的就是不管你这个数前面多少次0或者1，我只看最后一次，于是利用map函数，根据该数的判断结果，对这个数进行标记，这样的标记是实时更新的，保证最后的是最后的判断结果，然后再嫌疑人放进另一个数组进行排序，并判断是一个还是多个，到这里大家都能解决，但就是做不对，我此前用的是int定义这个数，后面换成string就对了，和之前做的帅到没朋友也是一样的道理，当时没想明白，可在写博客的时候想起了，如果用int定义这个数，当0000编号类出现，就是前导零的时候，如果输出上不加以控制，那么势必不会输出前导零。 

#include<bits/stdc++.h>
using namespace std;
struct xx{
    string x;
    int y;
}s[10005];
bool cmp(xx a,xx b){
return a.x<b.x;
    }
int main(){
    int n,i,j=0;
    string a[10005];
    map<string,int>p;
    cin>>n;
    for(i=0;i<n;i++){
        cin>>s[i].x>>s[i].y;
        if(s[i].y==1)p[s[i].x]=1;
       else if(s[i].y==0)p[s[i].x]=0;
    }
    for(i=0;i<n;i++){
        if(p[s[i].x]==1)a[j++]=s[i].x;
        p[s[i].x]=0;
    }
    sort(a,a+j);
    for(i=0;i<j;i++){
 if(i!=0)cout<<" ";
        cout<<a[i];
    }
    cout<<endl;
    if(j==1)cout<<"Da Ben Zhong is found!";
    else printf("There are %d suspects.",j);
    return 0;
}

 B-4 真分数的约分

真分数是指分子小于分母的分数。对分数进行约分，是指将分子分母共同的因子消去。

但还有一种另类的简单约分：直接将分子分母共有的一对数字消去。这种方法大多数情况下都得不到正确的结果，但有时候却也碰巧能对！例如 26/65 = 2/5 就是直接消去 6 的结果。

现给定一个真分数，你的任务是判断它是否能用简单约分方法得到正确结果。注意：如果有多种简单约分的可能，一定按从左到右的顺序约掉数字。

输入格式：

输入在一行中给出一个真分数的分子 a 和分母 b，其间以空格分隔。题目保证 0<a<b≤105。

输出格式：

在一行中先后输出这个真分数在简单约分前后的样子。如果两个分数相等，则在两者间加一个 = 号；否则加一个 != 号。格式为 a/b = c/d 或 a/b != c/d。

输入样例 1：

39 195

输出样例 1：

39/195 = 3/15

输入样例 2：

1234 23452

输出样例 2：

1234/23452 != 1/52

输入样例 3：

1234 5678

输出样例 3：

1234/5678 = 1234/5678

//这题就表示我做错的地方，直接解析。首先输入两个整数，为了方便转为字符串处理，对分子从左往右循环，k=0，然后对分母从左往右循环，如果分子的数，等于分母的数且保证这个分母的数的位置没被标记，那么我们就标记，k=1表示分子当前这个位置的数被删除了，p[j]=1表示分母上的这个位置的数被删除了，然后判断k值，如果没被标记，用x存起来，后面再循环判断没被标记的分母再用y存起来，最后判断输出，这里需要注意判断的精度问题，然后还有一个样例点，就是当x和y为0的时候，需要特判一下

#include<bits/stdc++.h>
using namespace std;
int main(){
  string a,b;  int i,x=0,y=0,j,a1,b1;
    cin>>a1>>b1;
    a=to_string(a1);b=to_string(b1);
    map<int,int>p;
    for(i=0;i<a.size();i++){
        int k=0;
        for(j=0;j<b.size();j++){
            if(a[i]==b[j]&&p[j]==0){k=1;p[j]=1;break;}
        }
        if(k==0)x=x*10+(a[i]-'0');
    }
    for(j=0;j<b.size();j++){
        if(p[j]==0) y=y*10+(b[j]-'0');
    }
     if(x==0&&y==0)printf("%d/%d != %d/%d",a1,b1,x,y);
    else 
    {if(a1*1.0/x==b1*1.0/y)printf("%d/%d = %d/%d",a1,b1,x,y);
    else printf("%d/%d != %d/%d",a1,b1,x,y);}
    return 0;
}

 

 B-5 取行李

一般机场里，航班到达后，旅客们会去到达区的行李传送带那里取自己的行李。

现假设有一座特别的机场，每条传送带只有一个取行李的窗口。旅客们必须排好队，逐一到窗口取自己的行李。但是当某人到窗口前，发现行李不是自己的，那人就只好走到队尾去等下一次机会。此时那件行李会一直等在窗口，直到它的主人把它取走。假设每一次认领需要 1 分钟，本题就要求你计算传送带清空需要的时间、以及旅客们的平均等待时间。

例如，假设行李 i 属于旅客 i。行李的到达顺序是 1、2、3，旅客的到达顺序是 2、1、3。则 1 号行李要等 2 分钟才能被主人 1 号旅客取走。这时行李队列中有 2、3，旅客队列中是 3、2。于是 2 号行李还要等 2 分钟才能被 2 号旅客取走，最后 3 号在第 5 分钟取走行李。旅客们的平均等待时间是 (2+4+5)/3≈3.7。

输入格式：

输入首先在第一行给出一个正整数 N（≤103）。下一行给出 N 个数字，是 [1,N] 区间内整数的一个重排列，表示旅客队列。这里我们假设行李队列是按 1、2、……、N 有序的，并且行李 i 属于旅客 i。一行中数字间以空格分隔。

输出格式：

在一行中输出传送带清空需要的时间、以及旅客们的平均等待时间（输出小数点后 1 位）。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

5
3 5 1 2 4

输出样例：

9 6.0

//这道题算是有点作弊吧，知道要有队列，先进先出，后进后出，后面新加的元素都会放在队尾，但是平时练stl类的题太少了，map用的很多，其他的有点陌生，上次还写了stl浅析的博客以此巩固基础知识， 不过做的时候还是忘掉了，最基本的queue，我给写成了queen，入队的push写成了pshu_back,现在也记不起是哪里的知识点了

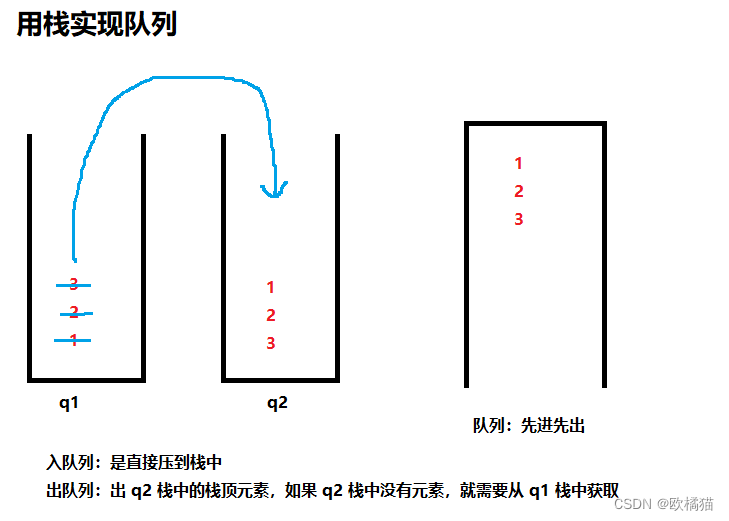
书归正转，我们用一数组存1-n的自然序列，也就是箱子顺序（不过现在看好像不用，直接和i变量对比就行），然后将题目的顾客顺序存进队列，之后循环，再循环判断，如果当前队头元素不等于当前箱子序号，那么就等一分钟，将队头元素放到队尾，等于之后，删掉这个队头，将时间存起来，后面就是时间的统计了，这里给个图形描述，还需要注意，因为如果当前队头就等于当前序号，就不进行第二个循环，但是这里都需要花费一分钟，所以x为1

代码还可以精简一点，不过当时只想着能做出来就好 

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,a[1005],i,c,x=0,z,d[1005],m=0,p=0; double y=0;
    queue<int>b;
    cin>>n;
    for(i=1;i<=n;i++)a[i]=i;
    for(i=1;i<=n;i++){
        cin>>c;
        b.push(c);
    }
    for(i=1;i<=n;i++){
        x=1;
       while(a[i]!=b.front()){
           x++;
           z=b.front();
           b.pop();
           b.push(z);
       }
        b.pop();
        d[i]=x;
    }
     for(i=1;i<=n;i++) m+=d[i];
     for(i=1;i<=n;i++){
         p=0;
         for(int j=1;j<=i;j++)
             p+=d[j];
         y+=p;
     }
    y=y*1.0/n;
    printf("%d %.1f",m,y);
    return 0;
}

 //下面分别附上我参加考试的同学当时他们的通关率和我后面花钱买习题的通关率，有些题看似难，但简单，而看起来简单的也确实简单，只是细节要处理到位，不要只盯着题目给的样例，要自己去找样例测试