比赛连接：传送门

密码：2023qsb

A.Zlz's problem(Easy Version)

题目描述：

This is the easy version of this problem. The only difference between the easy and hard versions is the constraints on n and m.

So I won't even take a glance

I would rather do my math

High on some calculus

I can forget about my past

Rather do my math - Robin Gan

Zlz has a bent for mathematics. He once participated in a high school math competition and got the first prize. Even now, he spends a lot of time thinking about mathematical problems. After enjoying the song Rather do my math, Zlz felt more enthusiastic about mathematics. Zlz was playing a card game. There were n cards numbered 1 to n. Each time he randomly selected m cards from these n cards. After that he took down the minimum number of the cards he selected and then put the cards back.

Suddenly, one mathematics problem occurred to him. He wanted to know the expectation of the number he took down. Could you please write a program to calculate the answer modulo 998244353.

输入描述：

Only one line contains two integers n,m -- the number of cards, the number of cards that Zlz will select.

It is guaranteed that for all test cases: 1≤n≤20 ;1≤m≤n.

输出描述：

Output an integer representing the answer modulo 998244353 in one line.

样例：

输入1：

3 2

输出1：

332748119

输入2：

5 3

输出2：

499122178

思路：

n很小，直接暴力二进制枚举n张卡片选和不选状态，只要状态中1的个数为m就算上贡献。

代码：

#include<bits/stdc++.h>
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=a;i>b;--i)
#define lowbit(x) ((x)&-(x))
using namespace std;
typedef long long LL;
const int MOD=998244353;
inline int Cnt(int x)
{
    int ct=0;
    while(x){
        ++ct;
        x-=lowbit(x);
    }
    return ct;
}
inline int Qp(int a,int b)
{
    int res=1;
    while(b){
        if(b&1) res=1ll*res*a%MOD;
        a=1ll*a*a%MOD;
        b>>=1;
    }
    return res%MOD;
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n,m;
    cin>>n>>m;
    int ans=0,cnt=0;
    rep(i,0,1<<n){
        if(Cnt(i)!=m) continue;
        ++cnt;
        rep(j,0,n) if(i>>j&1){
            ans=(ans+j+1)%MOD;
            break;
        }
    }
    ans=1ll*ans*Qp(cnt,MOD-2)%MOD;
    cout<<ans<<endl;
    return 0;
}

B.Tree Tree Tree

题目描述

HXT is a good student. He loves to clean the public health area on weekends.One day, while he was sweeping leaves, a question occurred to him. In front of him was a tree, consisting of n vertices. The vertices are numbered from 1 to n. The distance between two points on the tree is the number of sides contained in the shortest path between two points. HXT wants to know how many different pairs of points there are on the tree where the distance between the two points is exactly equal to k, which is a given number. Note: (u, v) and (v, u) are treated as the same point pair and the answer is calculated only once.

输入描述

The first line contains two integers, n and k(2≤n≤50000; 1≤k≤500).

输出描述

Next there are n-1 lines, each with two integers $a_{i}$ , $b_{i}$ , indicating that there is an edge between the node $a_{i}$ and $b_{i}$ .

样例

输入1：

输出1：

输入2：

输出2：

思路

用f[i][j]表示以i节点为根的子树中，与i的距离为j的个数。v为i的子节点，转移方程可以写为 $f[i][j]=\sum f[v][j-1]$

建好树后直接搜索一遍即可。对于节点u，他的一个子节点v，对答案的贡献就是 $\sum_{i=0}^{d-1} f[u][i] \cdot f[v][d-1-i]$ ，原来到u距离为i的方案数与到v距离为d-1-i方案数的乘积，表示距离为d的条数。注意一定要先更新答案，再用子节点更新f[u][i]。

代码

#include<bits/stdc++.h>
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=a;i>b;--i)
using namespace std;
typedef long long LL;
const int N=50010,M=510;
int h[N],ne[2*N],e[2*N],idx;
int n,k;
int f[N][M];
LL ans;
void Add(int a,int b)
{
    e[++idx]=b,ne[idx]=h[a],h[a]=idx;
}
void Dfs(int u,int fa)
{
    f[u][0]=1;
    for(int i=h[u];i;i=ne[i]){
        int j=e[i];
        if(j==fa) continue;
        Dfs(j,u);
        rep(d,0,k) ans+=1ll*f[u][d]*f[j][k-d-1];
        rep(d,1,k+1) f[u][d]+=f[j][d-1];
    }
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>k;
    rep(i,0,n-1){
        int a,b;
        cin>>a>>b;
        Add(a,b),Add(b,a);
    }
    Dfs(1,0);
    cout<<ans;
    return 0;
}

C.Lost stars

题目描述

And...God, tell us the reason youth is wasted on the young

It's hunting season and the lambs are on the run

Searching for meaning

But are we all lost stars trying to light up the dark?

lost stars - Maroon 5

Just as Wild_pointer was listening to lost stars, academician Zhou sent a ICPC training problem for him. "I had AC this problem, foolish Wild_pointer come to solve it." said academician Zhou ironically. Wild_pointer immediately wrote a brute force algorithm and submitted. Unfortunately he got TLE for he mistook the data scale. It's quite certain that his program is correct. What is needed is improvement of the time and space complexity of the algorithm. Wild_pointer is such a fool. But he is afraid of being laughed at by academician Zhou. As an excellent algorithm competition contestant, could you please help him?

Wild_pointer's code was written in Python:

n=int(input())
global g
g=0
fib=[0,1]
def Dfs(n,s,p):
    global g
    if n==0:
        g=(g+s)%p
        return
    for i in range(1,n+1):
        Dfs(n-i,s*fib[i]%p,p)
for i in range(2,n+1): fib.append(fib[i-1]+fib[i-2])
q=9614361054979589693
Dfs(n,1,q)
print(g)

Please write a program to ensure that he can get AC.

Note that for the same input, the answer output of your program must be consistent with Wild_pointer's program output, and your program must meet the limitations of this problem.

输入描述

Only one line contains an integer n. ( $1\le n \le 10^{100000}$ )

输出描述

Output an integer representing the answer in one line.

样例

输入1：

输出1：

输出2：

思路：

设 $a_{i}$ (i≥1)为n=i的时候对应的答案， $a_1=1,a_2=2$ ，打表找规律可以发现该数列的递推关系： $a_{n}=2a_{n-1}+a_{n-2}$

证明：

由代码中Dfs函数可知： $a_n=\sum_{i=1}^{n-1} a_{n-i}\cdot f_i=\sum_{i=1}^{n-1} a_{i}\cdot f_{n-i}$

$a_n-a_{n-1}=\sum_{i=1}^{n-1} a_{i}\cdot f_{n-i} -\sum_{i=1}^{n-2} a_{i}\cdot f_{n-i-1} \\ =a_{n-1} \cdot f_{1}+\sum_{i=1}^{n-2} a_{i}\cdot f_{n-i} -\sum_{i=1}^{n-2} a_{i}\cdot f_{n-i-1} \\ =a_{n-1}+\sum_{i=1}^{n-2}a_i \cdot (f_{n-i}-f_{n-i-1}) \\ =a_{n-1}+\sum_{i=1}^{n-2}a_i \cdot f_{n-i-2} \\ =a_{n-1}+a_{n-2}$

再把递推式写成矩阵的形式：

$\begin{bmatrix} a_{n}\\ a_{n-1} \end{bmatrix} =\begin{bmatrix} 2 & 1\\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_{n-1}\\ a_{n-2} \end{bmatrix} =\begin{bmatrix} 2 & 1\\ 1 & 0 \end{bmatrix}^{n-2} \cdot \begin{bmatrix} a_{2}\\ a_{1} \end{bmatrix}$

随后直接写矩阵快速幂即可，先用欧拉降幂公式更快，不用也能AC。

代码：

q=9614361054979589693
def Mul(a, b):
    c = [[0, 0], [0, 0]]
    for i in range(2):
        for j in range(2):
            for k in range(2):
                c[i][j] += a[i][k] * b[k][j]%q
                c[i][j]%=q
    return c
def Qp(n):
    if n <= 1: return max(n, 0)
    res = [[1, 0], [0, 1]]
    A = [[2, 1], [1, 0]]
    while n:
        if n & 1: res = Mul(res, A)
        A = Mul(A, A)
        n >>= 1
    return (res[0][0]*2+res[0][1])%q
n=int(input())
if n==1: print(1)
elif n==2: print(2)
elif n==3: print(5)
else: print(Qp(n-2))

D.Binary Problem

题目描述：

DHR is thinking about how to create a question. He is working out a problem with binary algorithms.

There are n quests. If you complete the i-th quest, you will gain aia_iai coins. You can only complete at most one quest per day. However, once you complete a quest, you cannot do the same quest again for k days. (For example, if k=2 and you do quest 1 on day 1, then you can not do it on day 2 or 3, but you can do it again on day 4.)

You are given two integers c and d. Find the maximum value of k such that you can gain at least c coins over d days. If no such k exists, output Impossible. If k can be arbitrarily large, output Infinity.

输入描述：

The first line contains three integers n,c,d (2≤n≤2e5;1≤c≤1e16;1≤d≤2e5) — the number of quests, the number of coins you need, and the number of days.

The second line contains n integers a1,a2,…,an(1≤ai≤1e9) — the rewards for the quests.

输出描述：

Output one of the following.

• If no such k exists, output Impossible.

• If k can be arbitrarily large, output Infinity.

• Otherwise, output a single integer — the maximum value of k such that you can gain at least c coins over d days.

样例：

输入1：

2 20 10
100 10

输出1：

Infinity

输入2：

3 100 3
7 2 6

输出2：

Impossible

输入3：

4 100000000000 2022
8217734 927368 26389746 627896974

输出3：

输入4：

2 20 4
5 1

输出4：

思路：

很常规的二分题。先将数组从大到小排序，对于不可能的情况，假设冷却时间为0，最优情况是d天都选最大的，如果仍达不到c说明不存在。对于任意大的情况，相当于每个数只能用一次，最优是选最大的d个数，如果大于等于c说明可以是任意大。

剩下的情况二分答案，假设一次最多完成x个任务（即k=x-1），贪心的选择最大的x个。可以证明最优选择是每一轮都选择最大的x个：前x天一定是选最大的x个，如果超过x天，第x+1天又可以选择第1个，第x+2天可以选择第2个...其他的选法都不会更优。

代码：

#include<bits/stdc++.h>
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=a;i>b;--i)
#define lowbit(x) ((x)&-(x))
using namespace std;
typedef long long LL;
const int MOD=998244353;
const int N=2e5+10;
int n,d,a[N];
LL c;
bool cmp(int x,int y)
{
    return x>y;
}
bool Che(int x)
{
    LL s=0;
    rep(i,0,min(x,n)) s+=a[i];
    int k=d/x,r=d%x;
    LL val=k*s;
    rep(i,0,min(r,n)) val+=a[i];
    return val>=c;
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>c>>d;
    rep(i,0,n) cin>>a[i];
    sort(a,a+n,cmp);
    if(1ll*a[0]*d<c){
        cout<<"Impossible";
        return 0;
    }
    LL s=0;
    rep(i,0,min(d,n)) s+=a[i];
    if(s>=c){
        cout<<"Infinity";
        return 0;
    }
    int l=1,r=2e5;
    while(l<r){
        int mid=l+r+1>>1;
        if(Che(mid)) l=mid;
        else r=mid-1;
    }
    cout<<l-1;
    return 0;
}

E.Zlz's problem(Hard Version)

输入描述：

Only one line contains two integers n,m -- the number of cards, the number of cards that Zlz will select.

For most test cases: 1≤n≤2000000;1≤m≤n. For some test cases: n=1e18,1≤m≤n.

输出描述：

Output an integer representing the answer modulo 998244353 in one line.

思路：

通过大部分数据，可以按照最小值分别计算概率。从1到n中选m个数，答案可以是1~n-m+1。选择的总方案数是C(n,m)，如果最小值为i，剩下的m-1个数一定比i大，故最小值为i的方案数为C(n-i,m-1)。

期望可以表示成： $\frac{\sum_{i=1}^{n-m+1} i\cdot C(n-i,m-1)}{C(n,m)}$

先预处理出阶乘及其逆元，枚举即可。

通过所有数据，只需要稍微化简一下分母，可以得到分母其实是 $C(n+1,m+1)$

$\sum_{i=1}^{n-m+1} i\cdot C(n-i,m-1)=C(n-1,m-1)+2C(n-2,m-1)+3C(n-3,m-1)+...+(n-m+1)C(m-1,m-1)\\=[C(n-1,m-1)+C(n-2,m-1)+...+C(m-1,m-1)] \\+[C(n-2,m-1)+C(n-3,m-1)+...+C(m-1,m-1)]\\+...+[C(m-1,m-1)]$

按照前面的思路，将C(n,m)按照选出的最小值划分，我们已经证明了：

$C(n,m)=\sum_{i=1}^{n-m+1} C(n-i,m-1)$

将中括号的运用上式合并，可以得到：

$C(n,m)+C(n-1,m)+...+C(m,m)=\sum_{i=0}^{n-m} C(n-i,m)=C(n+1,m+1)$

于是期望可以表示成 $\frac{n+1}{m+1}$

代码：

代码1（通过大部分数据）

#include<bits/stdc++.h>
#define endl '\n'
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=a;i>b;--i)
#define lowbit(x) ((x)&-(x))
using namespace std;
typedef long long LL;
const int MOD=998244353;
const int N=2e6+10;
int f[N],g[N];
int Qp(int a,int b)
{
        int res=1;
        while(b){
                if(b&1) res=1ll*res*a%MOD;
                b>>=1;
                a=1ll*a*a%MOD;
        }
        return res%MOD;
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n,m;
    cin>>n>>m;
    f[0]=g[0]=1;
    rep(i,1,n+1) f[i]=1ll*i*f[i-1]%MOD,g[i]=1ll*g[i-1]*Qp(i,MOD-2)%MOD;
    int ans=0,val=1ll*m*f[n-m]%MOD*g[n]%MOD;
    rep(i,1,n-m+2){
        ans=(ans+1ll*i*f[n-i]%MOD*g[n-i-m+1]%MOD*val%MOD)%MOD;
    }
    cout<<ans;
    return 0;
}

代码2（通过所有数据）

n,m=map(int,input().split())
q=998244353
print((n+1)%q*pow(m+1,q-2,q)%q)

F.Surveillance System

题目描述：

Oops my baby, you woke up in my bed

Oops we broke up, we're better off as friends

Now I accidentally need you

I don't know what to do

Oops baby I love you

Oops - Little Mix&Charlie Puth

Dhr had a date with his girlfriend. As the music player was playing Oops, Dhr felt that it was time to propose to his girlfriend. However, when he was looking for the ring he had bought, he found that it had been stolen. Dhr called the cops to find the thief. Unfortunately, the city had no surveillance system and can't find the trace of thieves.The local government attaches great importance to such theft cases and has decided to establish a secure surveillance system for the region.

To simplify this problem, a region can be seen as a square with side length n, where n is an even number.

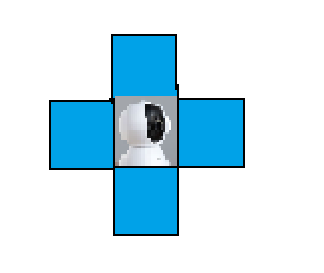
We can divide the region into n * n units, where 1 unit is a square with a side length of 1. The government has decided to choose certain units to install surveillance cameras. After installing a camera in a certain unit, it can monitor its adjacent 4 units(two units are adjacent if and only if they have a common edge.), as shown in the following figure.

Due to current financial constraints, the government wants to use as few surveillance cameras as possible to ensure that any unit in the region is monitored by at least one surveillance camera.

Note that the surveillance camera can not monitor its own unit, so you must ensure the adjacent unit has at least one surveillance camera to monitor it.

For example, when n=2, the answer is 2. One reasonable surveillance camera arrangement is shown in the following figure.

It can be seen that this arrangement ensures that each unit is monitored by at least one surveillance camera.

输入描述：

Each test contains multiple test cases. The first line contains the number of test cases t.The only line of each testcase contains one integer n, represents the length of the square region.It's guaranteed that n is even, 2≤n≤1000000000, and 1≤t≤100000.

输出描述：

Output an integer representing the answer in one line for each test.

样例：

输入1：

2
2
4

输出1：

2
6

思路：

本题猜结论容易，证明难。打表打出n=2,4,6,8,10对应的答案是2,6,12,20,30。~~如果你的数感足够好的话，可以看出规模n的最小点数为~~ $\frac{n(n+2)}{4}$

证明：

为了形象一点，我会举出n=2,4,6的例子。

设 $n=2k(k \in N^*)$ ，先将格子划分成黑蓝相间。

我们需要证明答案为 $\frac{n(n+2)}{4}$ ，即证明答案为 $k(k+1)$ 。我们考虑在蓝色方块上放上监视器，使得器任意黑色格子都至少有一个监视器，设满足这个条件需要放a个监视器。

考虑如下方法（图中黄点表示放置监视器）：

具体的方法，可以采用动态规划来理解。我们从对角线的方向来看图形，设f[k]是对于规模k的上三角形最小放置个数，考虑最底层的黑边，在上面一层的蓝色奇数位置放上监视器，可以发现这样下面两层黑边就满足了，状态转移到了f[k-2]。

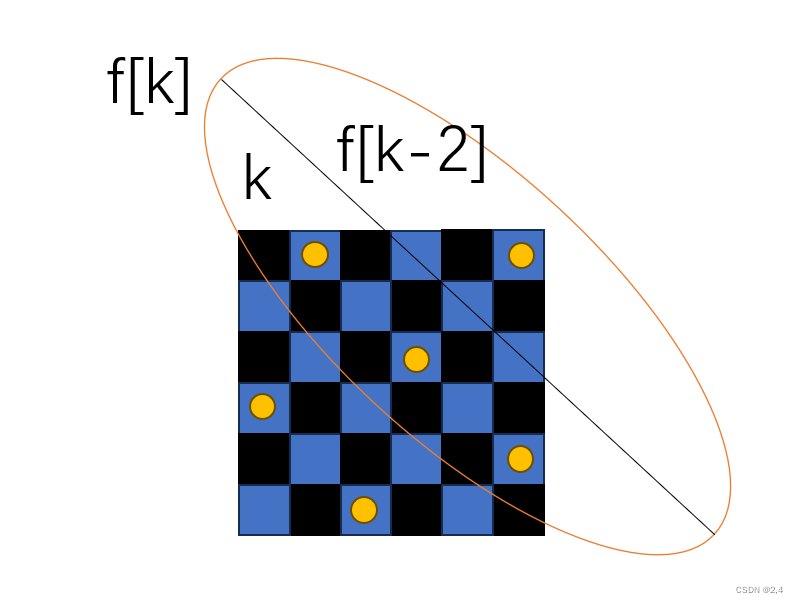
转移方程： $f[k]=k+f[k-2]$

对于正方形，放置的个数就是： $a=f[k]+f[k-1]$

然后结合转移方程化简一下：

$a=f[k]+f[k-1]=k+(k-1)+f[k-2]+f[k-3]=k+(k-1)+(k-2)+...+1=\frac{k(k+1)}{2}$

然后考虑在黑色方块上放上监视器，使得器任意蓝色格子都至少有一个监视器，设满足这个条件需要放b个监视器。其实因为图形是对称的，所以，这两个方面是对称的。话句话说，对于最优方案，有a=b。

非严谨的证明到这里已经结束啦！因为刚才在做动态规划的时候，可以基本确认这种方案摆出的 $\frac{k(k+1)}{2}$ 就是最小值，这样答案就是 $a+b=2a=k(k+1)$ ，命题得证。

如果要严谨的证明，我们前面其实是证明了 $a\ge\frac{k(k+1)}{2}$ ，现在我们试图证明 $a\le \frac{k(k+1)}{2}$ 。

现在从黑色这里入手，观察按照刚才在蓝色方块放了监视器的这些位置，你会发现它们所监视的黑色方格是没有重合的！要保证这些蓝色方格被监视到，至少需要放置 $\frac{k(k+1)}{2}$ ，于是有 $b\ge \frac{k(k+1)}{2}$

别忘了在取最小值时 $a=b$ ，则有 $a=b=\frac{k(k+1)}{2}$

综上，整个命题就证明完了。

代码：

#include<bits/stdc++.h>
#define endl '\n'
#define fi first
#define se second
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=a;i>b;--i)
typedef long long LL;
using namespace std;
const int N=1e6+10;
int main()
{
        ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
        int T,n;
        cin>>T;
        while(T--){
                cin>>n;
                cout<<1ll*n*(n+2)/4<<endl;
        }
        return 0;
}

G.Koyuki's problem

题目描述：

いつか好きになる気づいた

あと何回ねえ目が合えば

カウントダウン止まって

認めたら認めちゃったら

隠す声が震えちゃうんだ

今好きになる

今好きになる - HoneyWorks

One day Hina made up her mind to profess her love to Koyuki. Koyuki, as a senior, was going to prepare a simple problem to test her. Once upon a time, Gauss's teacher asked him to calculate the sum of 1 to 100. And Gauss came up with the summation formula. Koyuki also wanted Hina to calculate the sum of some numbers. To keep Hina away from the summation formula, Koyuki gave Hina some integers and operation symbols. There are only two types of operation symbols: addition and subtraction. The value was equal to zero from the beginning. Hina had to use all of the operation symbols and choose some integers Koyuki gave to maximize the value.

This problem was too computationally demanding for Hina. So she hopes you can write a program to help her calculate the answer within one second.

输入描述：

The first line contains three integers n,p,q -- the number of given integers, the number of given plus signs, the number of given minus signs.

The second line contains n integers $a_{1},a_{2},...,a_{n}$ -- the integers that Koyuki gave.

All the integers are separated by a blank space.

It is guaranteed that for all test cases:1≤n≤2000000;−1e9≤ai≤1e9;p+q≤n;p,q≥0

输出描述：

Output an integer representing the answer in one line.

思路：

将所有给出的数排序，所有正号给最大的，所有负号给最小的。

代码：

#include<bits/stdc++.h>
#define endl '\n'
#define fi first
#define se second
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=a;i>b;--i)
typedef long long LL;
using namespace std;
const int N=2e6+10;
int a[N];
int main()
{
        ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
        int n,p,q;
        cin>>n>>p>>q;
        rep(i,0,n) cin>>a[i];
        sort(a,a+n);
        LL ans=0;
        rep(i,0,q) ans-=a[i];
        per(i,n-1,n-p-1) ans+=a[i];
        cout<<ans<<endl;
        return 0;
}

H.GTA Ⅲ

题目描述

Tell me why, ain't nothin' but a heartache

Tell me why, ain't nothin' but a mistake

Tell me why, I never wanna hear you say

I want it that way

I Want It That Way - Backstreet Boys

Hxt was playing GTA Ⅲ. He felt he was racing on the streets of Liberty City while enjoying I Want It That Way. He had to pass a mission. His job, decoy, to distract the cops. Hxt decided to choose a starting point, and drive clockwise along the loop once and then return to this place. There are some tools along the way. When the vehicle encounters one tool, its durability will be increased by 1. The cops, however, placed roadblocks on the roundabout. When the vehicle encounters one roadblock, its durability will be decreased by 1. The vehicle will explode when its durability becomes 0. Unfortunately, the vehicle that Hxt drove had only one durability left due to being attacked by cops. He hope to find a place to start and ensure the safety of his vehicle.

To simplify the problem, Hxt will choose the starting place at one of the tool.

输入描述：

The first line contains one integer n--the number of tools and roadblocks.

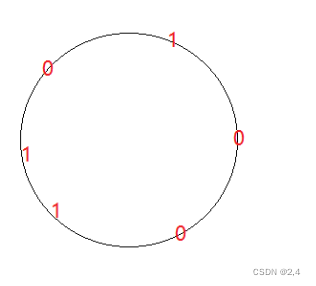
The second line contains a string of length n. The string only contains char '0' and '1'. '1' represents a tool and '0' represents a roadblock. The string represents starting from a certain point, the situation of various roadblock or tools in a clockwise direction.

For example, if the string is '100110', it can represent this case:

It is guaranteed that for all test cases: 1≤n≤5000000

输出描述：

Output the index of the starting place you find in the string. Output -1 if you can't find any. If there are multiple solutions, print the minimum of them.

Note that the index of the string starts from 1.

思路：

可以转换为从一个循环字符串中选择一个点，循环一次回到这个点的过程中，不能出现'0'比'1'多的情况。

暴力做法是枚举每个起始点，对每个起始点检查一遍。复杂度最坏是 $O(n^2)$ 。下面考虑前缀和思想，假设起始为0，'1'为+1，'0'为-1，对于某一个起点来说，任意一点从起点开始的前缀和大于等于0，如果出现小于等于0则不合法。

对于某个起点i，假设在第j个点不合法了，i到j中的点都不可能做为起点：假设起点为k(i＜k≤j)， $\sum_{p=k}^{j} a_p=\sum_{p=i}^{j} a_p -\sum_{p=i}^{k-1} a_p$ ，其中 $\sum_{p=i}^{j} a_p <0$ ， $\sum_{p=i}^{k-1} a_p \ge 0$ ，故 $\sum_{p=k}^{j} a_p < 0$

这样时间复杂度为 $O(n)$ 。

代码：

#include<bits/stdc++.h>
#define endl '\n'
#define fi first
#define se second
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=a;i>b;--i)
typedef long long LL;
using namespace std;
const int N=1e7+10;
char s[N];
int main()
{
        ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
        int n;
        cin>>n>>s+1;
        rep(i,1,n+1) s[i+n]=s[i];
        rep(i,1,n+1){
                if(s[i]=='0') continue;
                int ct=0;
                rep(j,i,i+n){
                        if(s[j]=='1') ++ct;
                        else --ct;
                        if(ct<0){
                                i=j;
                                break;
                        }
                }
                if(ct>=0){
                        cout<<i<<endl;
                        return 0;
                }
        }
        cout<<-1<<endl;
        return 0;
}

I.Card game

题目描述：

Some day

いつか辿り着ける

きっと君に寄り添うため

何度もすれ違い

それでも信じて

道の先、空の向こう - Rita

Sora is playing a card game with Haruka.

There are n piles of cards on the table. And there is a positive integer on each card. The players take turns and Sora takes the first turn. In Sora's turn she takes a card from the top of any non-empty pile, and in Haruka's turn he takes a card from the bottom of any non-empty pile. Each player wants to maximize the total sum of the cards he took. The game ends when all piles become empty.

Suppose Sora and Haruka play optimally, what is the score of the game?

输入描述：

The first line contain an integer n( 1<=n<=100). Each of the next n lines contains a description of the pile: the first integer in the line is $s_{i}$ ( $1<=s_{i}<=100$ ) — the number of cards in the i-th pile; then follow $s_{i}$ positive integers $c_1$ , $c_2$ , ..., $c_k$ , ..., $c_{s_i}$ ( $1<=c_{k}<=1000$ )— the sequence of the numbers on the cards listed from top of the current pile to bottom of the pile.

输出描述：

Print two integers: the sum of Sora's cards and the sum of Haruka's cards if they play optimally.

样例：

输入1：

2
1 100
2 1 10

输出1：

101 10

输入2：

1
9 2 8 6 5 9 4 7 1 3

输出2：

30 15

输入3：

输出3：

18 18

思路：

原问题传送门

原问题洛谷题解传送门

codeforces上的一个比较经典的博弈问题。最优策略是对于偶数堆先手总去顶上一半的卡牌，后手取后面一半的卡牌。对于奇数堆，除去了中间的卡牌，策略和偶数一样，将所有奇数堆的中间的卡牌存入大顶堆中，先手后手依次取出。

对于偶数的牌堆，可以假设先手（取牌顶的人）企图拿到一张在后面二分之一的牌，对于后手来说，他都可以在先手同一个牌堆拿牌，使得这张牌一定不被先手拿到，反之，后手想要拿到一个更大的前二分之一的牌也会被先手阻止，最后的结果就是先手取掉前面二分之一的牌，后手取掉后面二分之一的牌。

对于奇数的牌，由于其他的牌一定是对称被抽出，我们可以把奇数堆中间的牌拿出来。这样最优策略是先手抽出最大的一张，后手抽出次大的一张...以此类推。

代码：

#include<bits/stdc++.h>
#define endl '\n'
#define fi first
#define se second
#define rep(i,a,b) for(int i=a;i<b;++i)
#define per(i,a,b) for(int i=a;i>b;--i)
typedef long long LL;
using namespace std;
int a[110];
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n;
    cin>>n;
    int s=0,h=0;
    priority_queue<int>q;
    while(n--){
        int ct;
        cin>>ct;
        rep(i,1,ct+1) cin>>a[i];
        if(ct&1) q.push(a[ct/2+1]);
        rep(i,1,ct+1){
            int j=ct-i+1;
            if(j<=i) break;
            s+=a[i],h+=a[j];
        }
    }
    bool fl=1;
    while(q.size()){
        if(fl) s+=q.top();
        else h+=q.top();
        fl=!fl;q.pop();
    }
    cout<<s<<" "<<h;
    return 0;
}