opencv基础41-图像梯度-sobel算子详解cv2.Sobel()（边缘检测基础）

图像梯度是用于描述图像变化率的概念。在图像处理中，梯度指的是图像中每个像素的灰度值变化速率或方向。它常用于边缘检测和图像特征提取。

一维图像的梯度表示为函数 f(x) 的导数，而在二维图像中，梯度是一个向量，包含两个分量：水平方向和垂直方向的灰度变化率。这两个分量的大小和方向可以用来确定图像中的边缘和纹理信息。

在图像处理中，常用的算子如Sobel、Prewitt和Scharr等可以用于计算图像的梯度。梯度计算对于计算机视觉任务和图像处理中的特征提取非常有用。

图像梯度计算需要求导数，但是图像梯度一般通过计算像素值的差来得到梯度的近似值（近似导数值）。

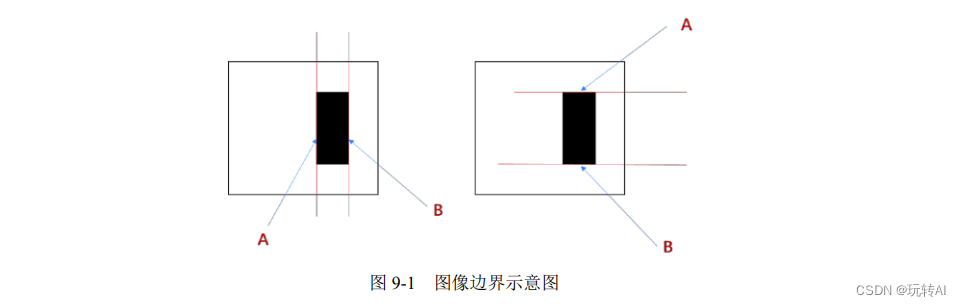
例如，图 9-1 中的左右两幅图分别描述了图像的水平边界和垂直边界。

针对左图，通过垂直方向的线条 A 和线条 B 的位置，可以计算图像水平方向的边界：

对于线条 A 和线条 B，其右侧像素值与左侧像素值的差值不为零，因此是边界。
对于其余列，其右侧像素值与左侧像素值的差值均为零，因此不是边界。

针对右图，通过水平方向的线条 A 和线条 B 的位置，可以计算图像垂直方向的边界：

对于线条 A 和线条 B，其下侧像素值与上侧像素值的差值不为零，因此是边界。
对于其余行，其下侧像素值与上侧像素值的差值均为零，因此不是边界。

在这里插入图片描述

将上述运算关系进一步优化，可以得到更复杂的边缘信息。

Sobel 理论基础

Sobel 算子是一种离散的微分算子，该算子结合了高斯平滑和微分求导运算。该算子利用局部差分寻找边缘，计算所得的是一个梯度的近似值。

Sobel 算子如图 9-2 所示。

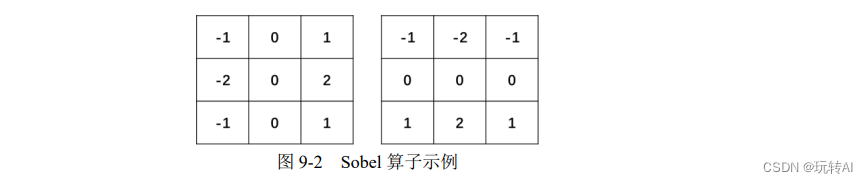
在这里插入图片描述
需要说明的是，滤波器通常是指由一幅图像根据像素点(x, y)临近的区域计算得到另外一幅新图像的算法。因此，滤波器是由邻域及预定义的操作构成的。滤波器规定了滤波时所采用的形状以及该区域内像素值的组成规律。滤波器也被称为“掩模”、“核”、“模板”、“窗口”、“算子”等。一般信号领域将其称为“滤波器”，数学领域将其称为“核”。

文中出现的滤波器多数为“线性滤波器”，也就是说，滤波的目标像素点的值等于原始像素值及其周围像素值的加权和。这种基于线性核的滤波，就是我们所熟悉的卷积。在文中，为了方便说明，直接使用“算子”来表示各种算子所使用的滤波器。例如，文中所说的“Sobel 算子”通常是指 Sobel滤波器。

假定有原始图像 src，下面对 Sobel 算子的计算进行讨论。

1. 计算水平方向偏导数的近似值

将 Sobel 算子与原始图像 src 进行卷积计算，可以计算水平方向上的像素值变化情况。
例如，当 Sobel 算子的大小为 3×3 时，水平方向偏导数 Gx的计算方式为：

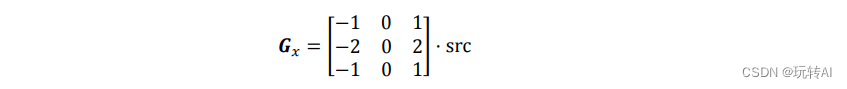
在这里插入图片描述
上式中，src 是原始图像，假设其中有 9 个像素点，如图 9-3 所示。

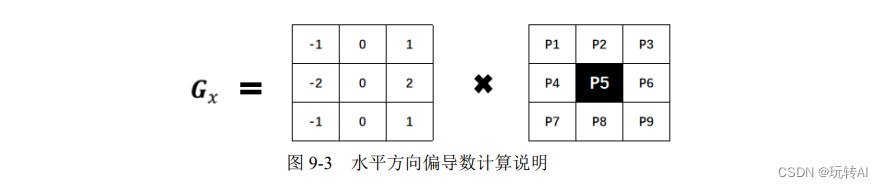
在这里插入图片描述
如果要计算像素点 P5 的水平方向偏导数 P5x，则需要利用 Sobel 算子及 P5 邻域点，所使用的公式为：

P5x = (P3-P1) + 2·(P6-P4) + (P9-P7)

即用像素点 P5 右侧像素点的像素值减去其左侧像素点的像素值。其中，中间像素点（P4 和 P6）距离像素点 P5 较近，其像素值差值的权重为 2；其余差值的权重为 1。

然后将这三个差值相加得到一个新的值，并将这个新的值赋给P5，即得到P5的像素值。

2. 计算垂直方向偏导数的近似值

将 Sobel 算子与原始图像 src 进行卷积计算，可以计算垂直方向上的变化情况。例如，当Sobel 算子的大小为 3×3 时，垂直方向偏导数 Gy的计算方式为：

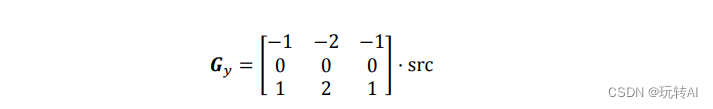
在这里插入图片描述

上式中，src 是原始图像，假设其中有 9 个像素点，如图 9-4 所示。

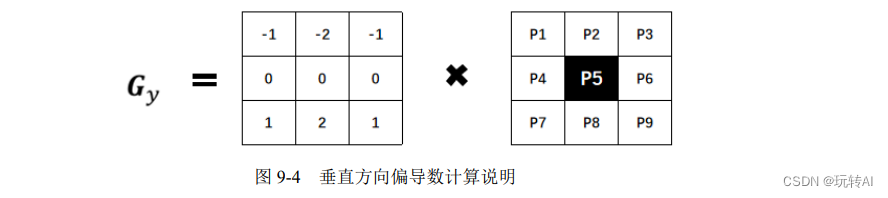
在这里插入图片描述
如果要计算像素点 P5 的垂直方向偏导数 P5y，则需要利用 Sobel 算子及 P5 邻域点，所使用的公式为：

P5y = (P7-P1) + 2·(P8-P2) + (P9-P3)

式中，使用像素点 P5 下一行像素点的像素值减去上一行像素点的像素值。其中，中间像素点（P2 和 P8）距离像素点 P5 较近，其像素值差值的权重为 2；其余差值的权重为 1。

Sobel 算子及函数使用

在 OpenCV 内，使用函数 cv2.Sobel()实现 Sobel 算子运算，其语法形式为：

dst = cv2.Sobel( src, ddepth, dx, dy[,ksize[, scale[, delta[, borderType]]]] )

式中：

dst 代表目标图像。
src 代表原始图像。
ddepth 代表输出图像的深度。其具体对应关系如表 9-1 所示。
dx 代表 x 方向上的求导阶数。
dy 代表 y 方向上的求导阶数。
ksize 代表 Sobel 核的大小。该值为-1 时，则会使用 Scharr 算子进行运算。
scale 代表计算导数值时所采用的缩放因子，默认情况下该值是 1，是没有缩放的。
delta 代表加在目标图像 dst 上的值，该值是可选的，默认为 0。
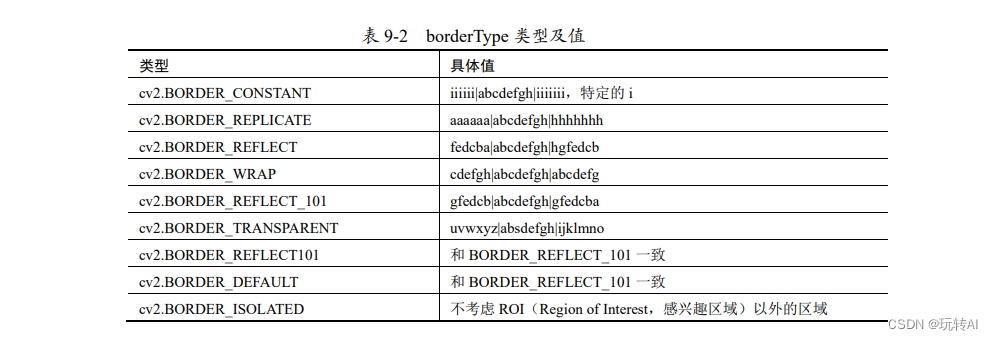
borderType 代表边界样式。该参数的具体类型及值如表 9-2 所示。

参数ddepth

在函数 cv2.Sobel()的语法中规定，可以将函数 cv2.Sobel()内 ddepth 参数的值设置为-1，让处理结果与原始图像保持一致。但是，如果直接将参数 ddepth 的值设置为-1，在计算时得到的结果可能是错误的。

在实际操作中，计算梯度值可能会出现负数。如果处理的图像是 8 位图类型，则在 ddepth的参数值为-1 时，意味着指定运算结果也是 8 位图类型，那么所有负数会自动截断为 0，发生信息丢失。为了避免信息丢失，在计算时要先使用更高的数据类型 cv2.CV_64F，再通过取绝对值将其映射为 cv2.CV_8U（8 位图）类型。所以，通常要将函数 cv2.Sobel()内参数 ddepth 的值设置为“cv2.CV_64F”。

下面对参数 ddepth 值的设定做一个简要的说明。

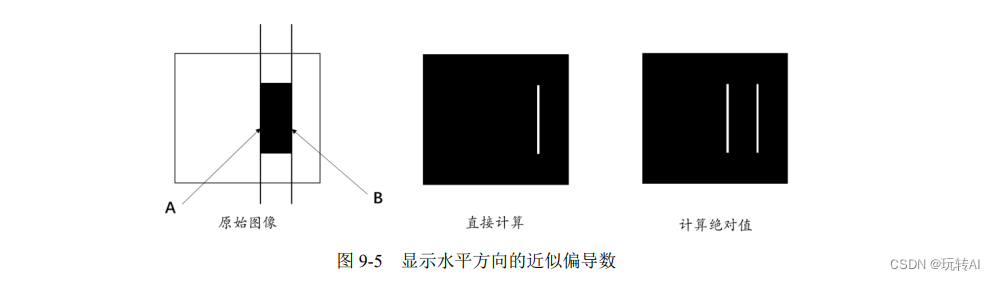
例如，图 9-5 中的原始图像（左图）是一幅二值图像，图中黑色部分的像素值为 0，白色部分的像素值为 1。在计算 A 线条所在位置和 B 线条所在位置的近似偏导数时：

针对 A 线条所在列，右侧像素值减去左侧像素值所得近似偏导数的值为-1。
针对 B 线条所在列，右侧像素值减去左侧像素值所得近似偏导数的值为 1。

针对上述偏导数结果进行不同方式的处理，可能会得到不同的结果，例如：

直接计算。此时，A 线条位置的值为负数，B 线条位置的值为正数。在显示时，由于上述负值不在 8 位图范围内，因此要做额外处理。将 A 线条处的负数偏导数处理为 0，B线条处的正数偏导数保持不变。在这种情况下，显示结果如图 9-5 中间的图所示。
计算绝对值。此时，A 线条处的负数偏导数被处理正数，B 线条处的正数偏导数保持不变。在显示时，由于上述值在 8 位图的表示范围内，因此不再对上述值进行处理，此时，
显示结果如图 9-5 中的右图所示。

在这里插入图片描述

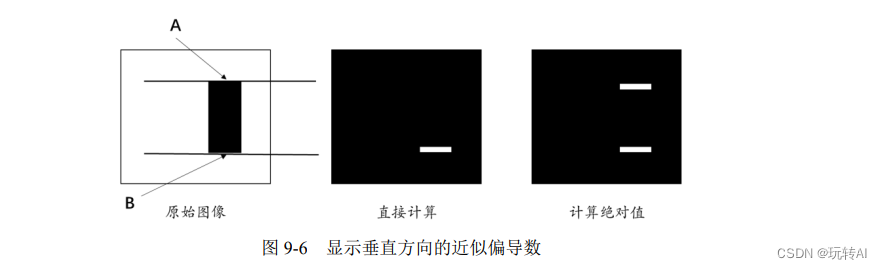
上述问题在计算垂直方向的近似偏导数时同样存在。例如，图 9-6 中的原始图像（左图）
是一幅二值图像，图中黑色部分的像素值为 0，白色部分的像素值为 1。计算 A 线条所在位置
和 B 线条所在位置的近似偏导数时：
 针对 A 线条所在行，下方像素值减去上方像素值所得近似偏导数为-1。
 针对 B 线条所在行，下方像素值减去上方像素值所得近似偏导数为 1。

针对上述偏导数结果进行不同方式的处理，可能会得到不同的结果，例如：

直接计算。此时，A 线条位置的值为负数，B 线条位置的值为正数。在显示时，上述值不在 8 位图的表示范围内，因此需要进行额外处理。将 A 线条处的负数偏导数处理为 0，
B 线条处的正数偏导数保持不变。此时，显示结果如图 9-6 中间的图所示。
计算绝对值。此时，A 线条处的负数偏导数被处理正数，B 线条处的正数偏导数保持不变。在显示时，由于上述值在 8 位图的表示范围内，因此不再对上述值进行处理，此时，
显示结果如图 9-6 中的右图所示。

经过上述分析可知，为了让偏导数正确地显示出来，需要将值为负数的近似偏导数转换为正数。即，要将偏导数取绝对值，以保证偏导数总能正确地显示出来。

例如，图 9-7 描述了如何计算偏导数。

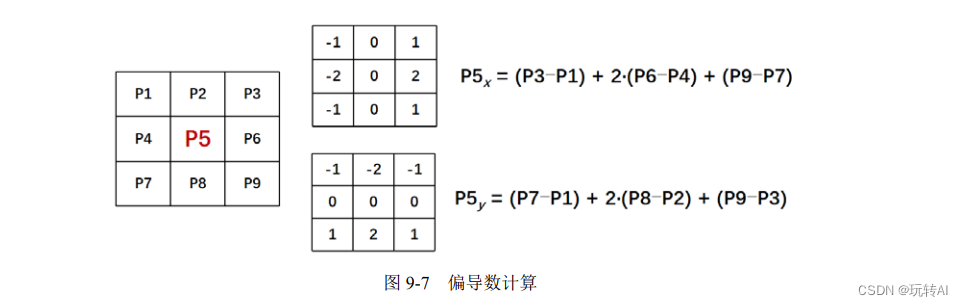
在这里插入图片描述
为了得到结果为正数的偏导数，需要对图 9-7 中计算的偏导数取绝对值，如下：

|P5x| = |(P3-P1) + 2·(P6-P4) + (P9-P7)|
|P5y| = |(P7-P1) + 2·(P8-P2) + (P9-P3)|

当然，在需要时，还可以进行如下处理：

P5Sobel = |P5x| + |P5y| = |(P3-P1) +2·(P6-P4) + (P9-P7)| + |(P7-P1) + 2·(P8-P2) + (P9-P3)|

经过以上分析，我们得知：在实际操作中，计算梯度值可能会出现负数。通常处理的图像是 8 位图类型，如果结果也是该类型，那么所有负数会自动截断为 0，发生信息丢失。所以，
为了避免信息丢失，我们在计算时使用更高的数据类型 cv2.CV_64F，再通过取绝对值将其映射为 cv2.CV_8U（8 位图）类型。

OpenCV 中，使用函数 cv2.convertScaleAbs()对参数取绝对值，该函数的语法格式为：

dst = cv2.convertScaleAbs( src [, alpha[, beta]] )

上式中：

dst 代表处理结果。
src 代表原始图像。
alpha 代表调节系数，该值是可选值，默认为 1。
beta 代表调节亮度值，该值是默认值，默认为 0。
这里，该函数的作用是将原始图像 src 转换为 256 色位图，其可以表示为：

dst=saturate(src*alpha+beta)

式中，saturate()表示计算结果的最大值是饱和值，例如当“src*alpha+beta”的值超过 255 时，其取值为 255。

代码示例：使用函数 cv2.convertScaleAbs()对一个随机数组取绝对值。

import cv2
import numpy as np
img=np.random.randint(-256,256,size=[4,5],dtype=np.int16)

rst=cv2.convertScaleAbs(img)
print("img=\n",img)
print("rst=\n",rst)

运行结果：

img=
 [[ -26 -176  -21 -125   70]
 [  54  156  -76   -8 -117]
 [ 226  -19  -21  114  132]
 [ 126  120   72 -256  137]]
rst=
 [[ 26 176  21 125  70]
 [ 54 156  76   8 117]
 [226  19  21 114 132]
 [126 120  72 255 137]]

从结果中看出原图中的负数都转变成了正数，并且转正大于255 的会改成255

cv2.Sobel() 方向参数 dx,dy

在函数 cv2.Sobel()中，参数 dx 表示 x 轴方向的求导阶数，参数 dy 表示 y 轴方向的求导阶数。参数 dx 和 dy 通常的值为 0 或者 1，最大值为 2。如果是 0，表示在该方向上没有求导。当然，参数 dx 和参数 dy 的值不能同时为 0。

参数 dx 和参数 dy 可以有多种形式的组合，主要包含：

计算 x 方向边缘（梯度）：dx=1, dy=0。
计算 y 方向边缘（梯度）：dx=0, dy=1。
参数 dx 与参数 dy 的值均为 1：dx=1, dy=1。
计算 x 方向和 y 方向的边缘叠加：通过组合方式实现。

下面分别对上述情况进行简要说明。

1. 计算x方向边缘（梯度）：dx=1,dy=0

如果想只计算 x 方向（水平方向）的边缘，需要将函数 cv2.Sobel()的参数 dx 和 dy 的值设置为“dx=1, dy=0”。当然，也可以设置为“dx=2, dy=0”。此时，会仅仅获取水平方向的边缘信息，此时的语法格式为：

dst = cv2.Sobel( src , ddepth , 1 , 0 )

使用该语句获取边缘图的示例如图 9-8 所示，其中左图为原始图像，右图为获取的边缘图。

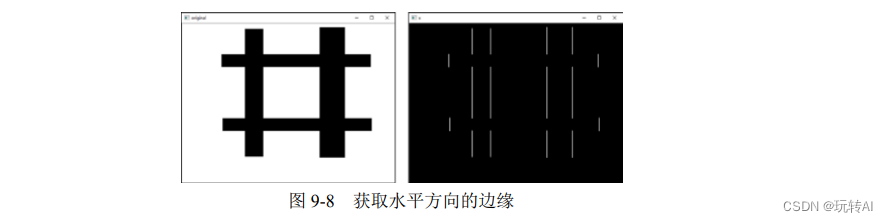
在这里插入图片描述

2. 计算y方向边缘（梯度）：dx=0,dy=1

如果想只计算 y 方向（垂直方向）的边缘，需要将函数 cv2.Sobel()的参数 dx 和 dy 的值设置为“dx=0, dy=1”。当然，也可以设置为“dx=0, dy=2”。此时，会仅仅获取垂直方向的边缘信
息，此时的语法格式为：

dst = cv2.Sobel( src , ddepth , 0 , 1 )

使用该语句获取边缘图的示例如图 9-9 所示，其中左图为原始图像，右图为获取的边缘图。

在这里插入图片描述

3. 参数dx与参数dy的值均为 1：dx=1,dy=1

可以将函数 cv2.Sobel()的参数 dx 和 dy 的值设置为“dx=1, dy=1”，也可以设置为“dx=2,dy=2”，或者两个参数都不为零的其他情况。此时，会获取两个方向的边缘信息，此时的语法格式为：

dst = cv2.Sobel( src , ddepth , 1 , 1 )

使用该语句获取边缘图的示例如图 9-10 所示，其中左图为原始图像，右图为获取的边缘图，仔细观察可以看到图中仅有若干个微小白点，每个点的大小为一个像素。

在这里插入图片描述

4. 计算x方向和y方向的边缘叠加

如果想获取 x 方向和 y 方向的边缘叠加，需要分别获取水平方向、垂直方向两个方向的边缘图，然后将二者相加。此时的语法格式为：

dx= cv2.Sobel( src , ddepth , 1 , 0 )
dy= cv2.Sobel( src , ddepth , 0 , 1 )
dst=cv2.addWeighted( src1 , alpha , src2 , beta , gamma ）

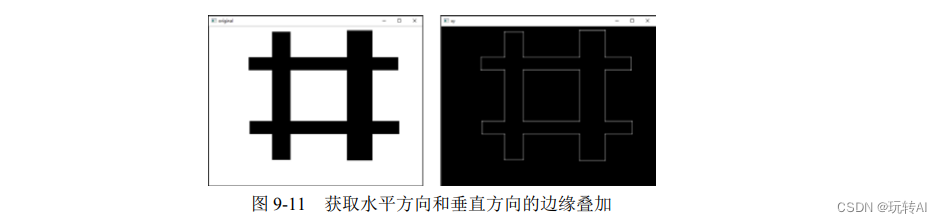
使用上述语句获取边缘图的示意图如图 9-11 所示，其中左图为原始图像，右图为获取的边缘图

在这里插入图片描述

代码示例：使用函数 cv2.Sobel()获取图像水平方向的边缘信息。

原图：
在这里插入图片描述

import cv2
o = cv2.imread('sobel4.bmp',cv2.IMREAD_GRAYSCALE)
Sobelx = cv2.Sobel(o,-1,1,0)
cv2.imshow("original",o)
cv2.imshow("x",Sobelx)
cv2.waitKey()
cv2.destroyAllWindows()

运行结果：

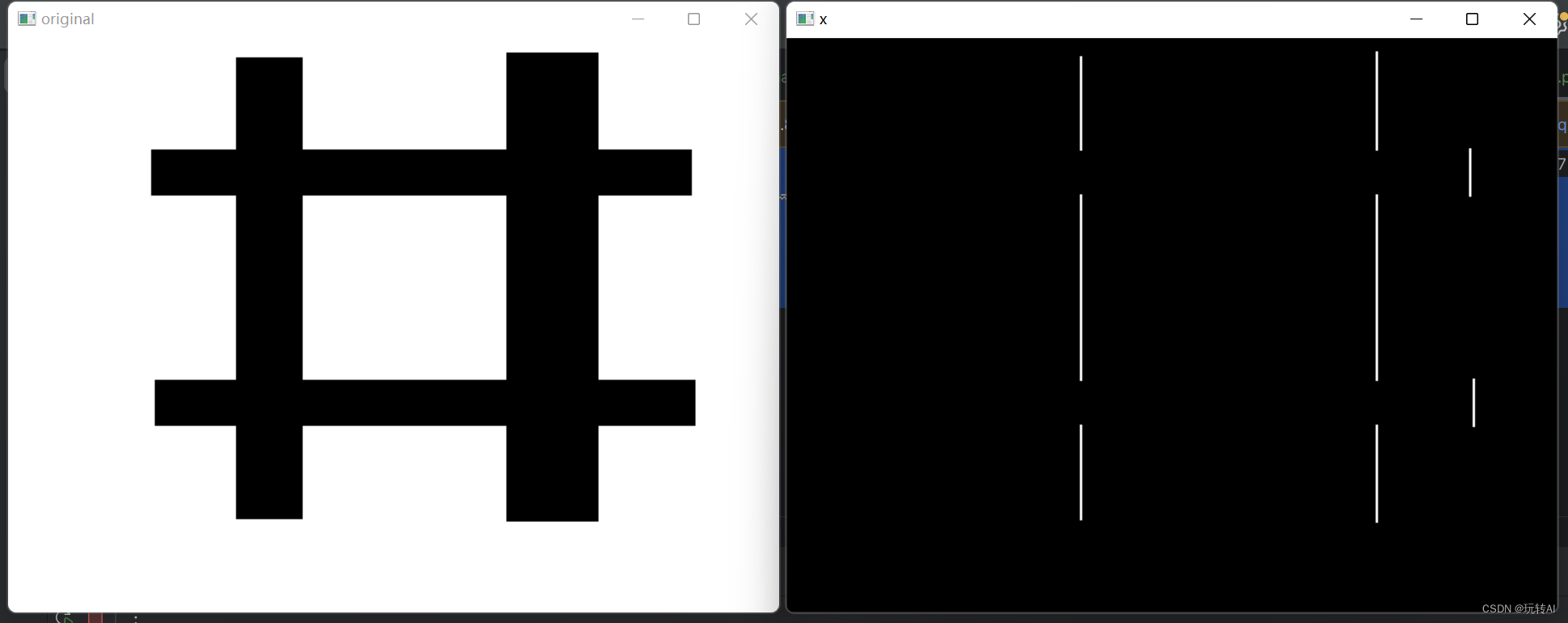
在这里插入图片描述
从程序可以看出，当参数 ddepth 的值为-1 时，只得到了图中黑色框的右边界。这是因为，左边界在运算时得到了负值，其在显示时被调整为 0，所以没有显示出来。要想获取左边界的值（将其显示出来），必须将参数 ddepth 的值设置为更大范围的数据结构类型，并将其映射到8 位图像内。

示例2：使用函数 cv2.Sobel()获取图像水平方向的完整边缘信息。

代码如下：

import cv2
o = cv2.imread('Sobel4.bmp',cv2.IMREAD_GRAYSCALE)
Sobelx = cv2.Sobel(o,cv2.CV_64F,1,0)
Sobelx = cv2.convertScaleAbs(Sobelx)
cv2.imshow("original",o)
cv2.imshow("x",Sobelx)
cv2.waitKey()
cv2.destroyAllWindows()

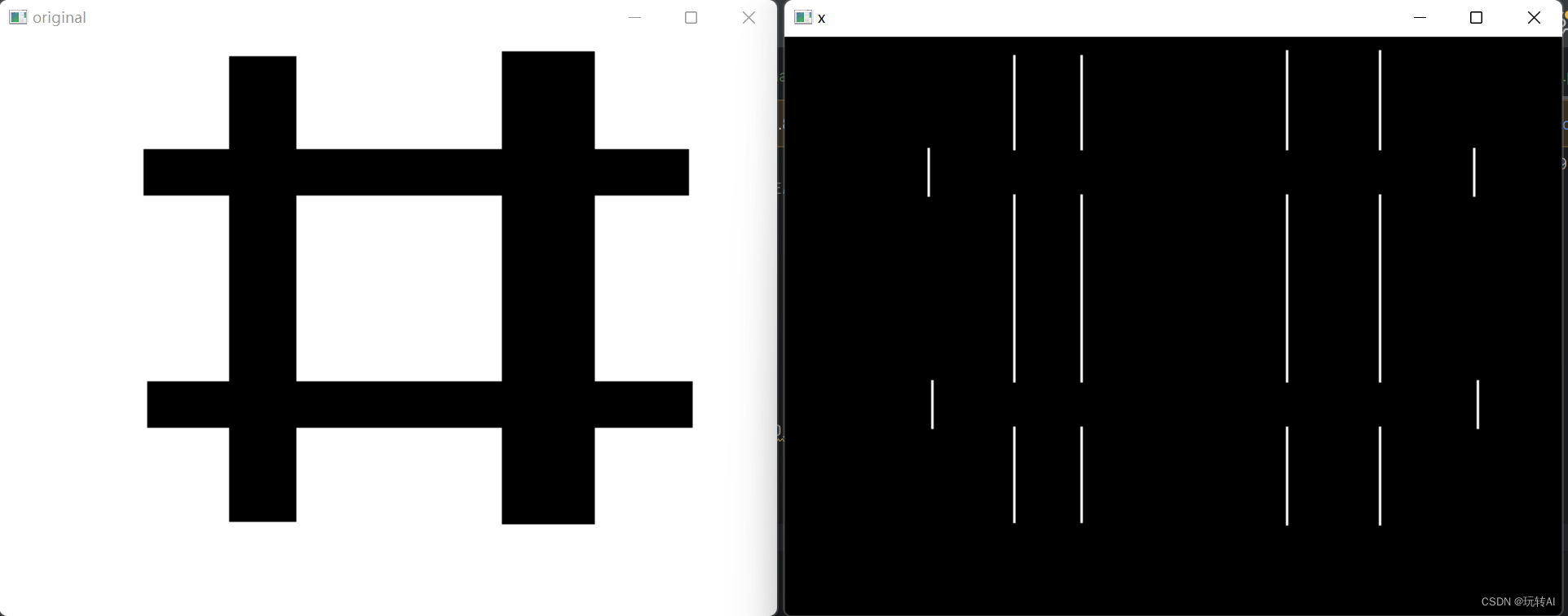
在这里插入图片描述

示例3：计算函数 cv2.Sobel()在水平、垂直两个方向叠加的边缘信息。

import cv2
o = cv2.imread('Sobel4.bmp',cv2.IMREAD_GRAYSCALE)
Sobelx = cv2.Sobel(o,cv2.CV_64F,1,0)
Sobely = cv2.Sobel(o,cv2.CV_64F,0,1)
Sobelx = cv2.convertScaleAbs(Sobelx)
Sobely = cv2.convertScaleAbs(Sobely)
Sobelxy = cv2.addWeighted(Sobelx,0.5,Sobely,0.5,0)
cv2.imshow("original",o)
cv2.imshow("xy",Sobelxy)
cv2.waitKey()
cv2.destroyAllWindows()

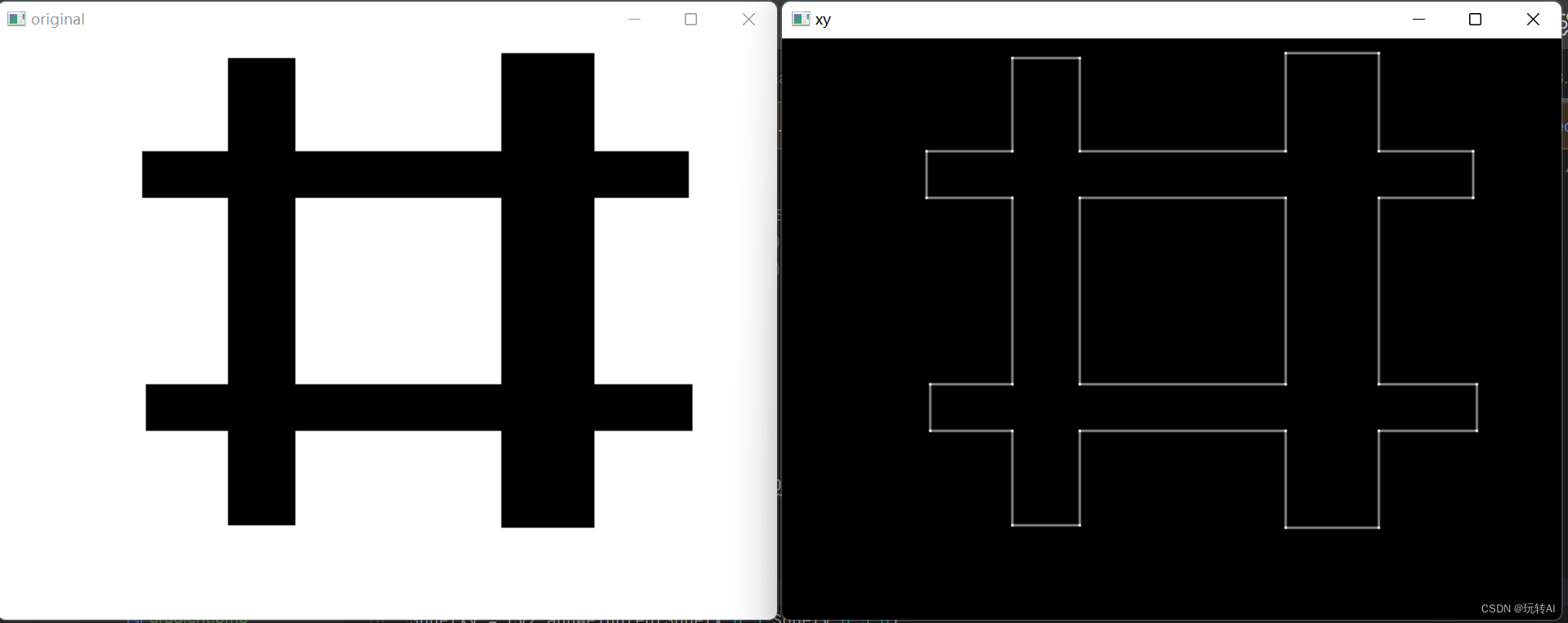
在这里插入图片描述
本例中首先分别计算 x 方向的边缘、y 方向的边缘，接下来使用函数
cv2.addWeighted()对两个方向的边缘进行叠加。在最终的叠加边缘结果中，同时显示两个方向的边缘信息。