第三章 图论 No.5最小生成树之虚拟源点，完全图与次小生成树

news2024/9/20 5:59:49

文章目录

      • 虚拟源点：1146. 新的开始
      • 贪心或kruskal性质：1145. 北极通讯网络
      • 最小生成树与完全图：346. 走廊泼水节
      • 次小生成树：1148. 秘密的牛奶运输

虚拟源点：1146. 新的开始

1146. 新的开始 - AcWing题库
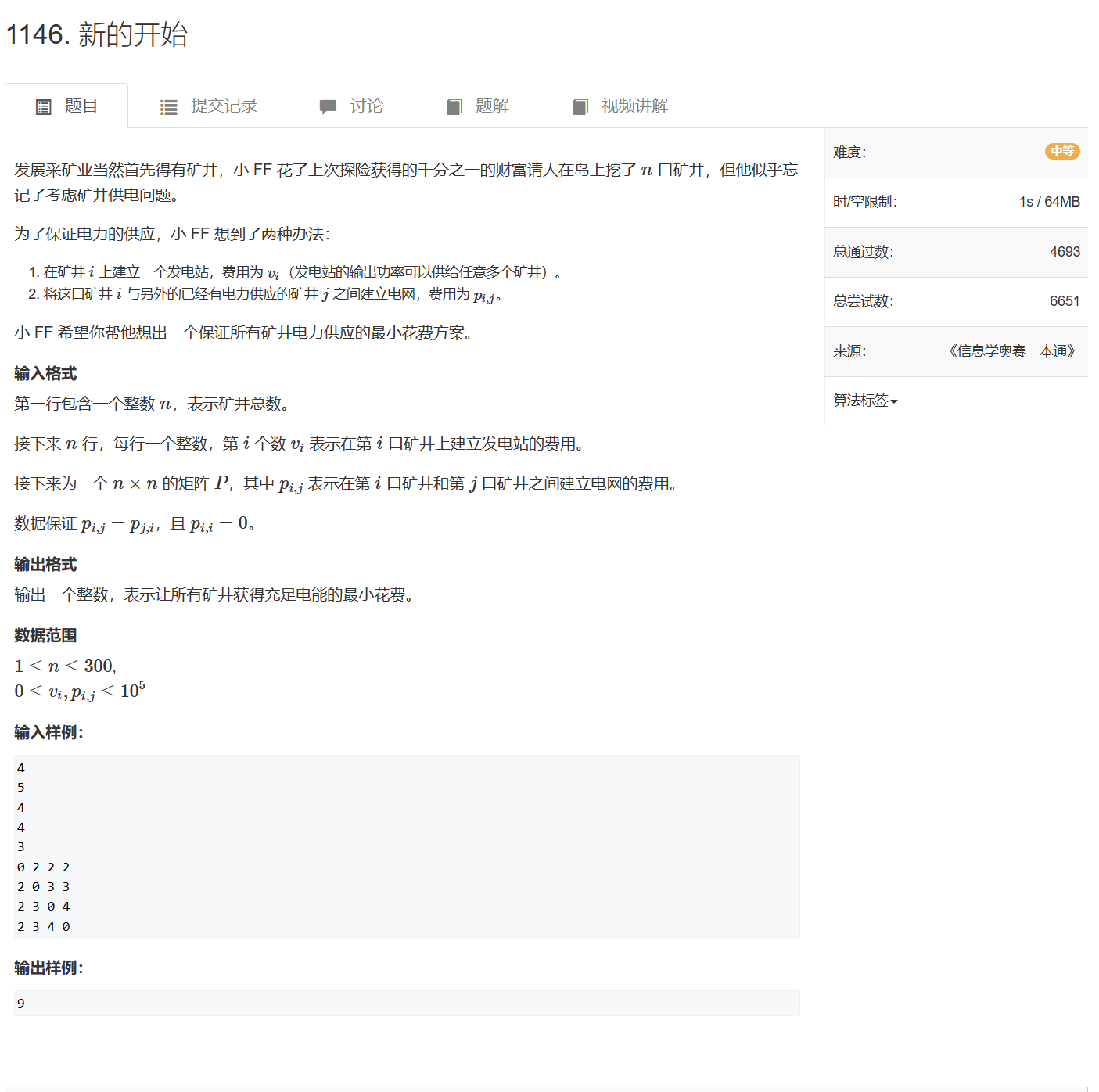
image.png

与一般的最小生成树问题不同，本题需要在建立电站的电井之间建立电网，在两个电站之间建立电网需要花费金额，可以看成一条具有权值的边
但是建立电网的前提是：其中一个电井需要建立电站，建立电站也需要费用
已经建立电站的两个电井之间无需建立电网，即一张电网中只需要存在一个建立电站的电井
可以将建立电站也看成具有权值的边，设置虚拟源点，在第i个电井建立电站可以转换成虚拟源点与i点之间的边，权值为建立电站的费用
此时跑个最小生成树即可

为什么不能直接跑最小生成树，再选择某个点建立一个最便宜的电站？只建立一个电站虽然能保证所有电井有电，但是两个电井建立电网的费用可能高于直接建立电站的费用
所以可能会建立多个电站，即最小生成“森林”，设置虚拟选点就是将每个森林连接，即最小生成树，此时需要跑最小生成树的算法即可

// 跑一遍最小生成树，记录其中点的最小值
#include <iostream>
#include <cstring>
using namespace std;

const int N = 310;
int g[N][N], dis[N];
bool st[N];
int n;

int prim()
{
    memset(dis, 0x3f, sizeof(dis));
    int res = 0;
    for (int i = 0; i <= n; ++ i )
    {
        int x = -1;
        for (int j = 0; j <= n; ++ j )
            if (!st[j] && (x == -1 || dis[x] > dis[j])) x = j;
        st[x] = true;
        if (i) res += dis[x];
        for (int y = 0; y <= n; ++ y )
            dis[y] = min(dis[y], g[x][y]);
    }
    return res;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i ) 
    {
        scanf("%d", &g[0][i]);
        g[i][0] = g[0][i];
    }
    for (int i = 1; i <= n; ++i )
        for (int j = 1; j <= n; ++ j )
            scanf("%d", &g[i][j]);
            
    printf("%d\n", prim());
    
    return 0;
}

贪心或kruskal性质：1145. 北极通讯网络

1145. 北极通讯网络 - AcWing题库
image.png

三种解法，第一种，一眼想到的就是贪心：
跑个最小生成树，升序记录所有边权
若有k个卫星，选择第k大的边即可，因为k个卫星使得k个村庄可以直接通信
k-1条最大边连接的村庄用卫星，其他用发电设备通信，此时d为最大的边权

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;

#define x first
#define y second
typedef pair<int, int> PII;
const int N = 510, INF = 0x3f3f3f3f;
double g[N][N], res[N];
double dis[N];
PII a[N];
bool st[N];
int n, k;

double get_dis(PII a, PII b)
{
    int x = a.x - b.x, y = a.y - b.y;
    return sqrt(x * x + y * y);
}

double prim()
{
    for (int i = 1; i <= n; ++ i ) dis[i] = INF;
    for (int i = 0; i < n; ++ i )
    {
        int x = -1;
        for (int j = 1; j <= n; ++ j )
            if (!st[j] && (x == -1 || dis[x] > dis[j])) x = j;
        st[x] = true;
        if (i) res[i] = dis[x];
        
        for (int y = 1; y <= n; ++ y )
            dis[y] = min(dis[y], g[x][y]);
    }
    sort(res + 1, res + n);
    return res[n - k]; // 1 ~ n-1 为最小生成树的边权升序排序
}

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; ++ i )
        scanf("%d%d", &a[i].x, &a[i].y);
    
    if (k >= n) puts("0.00");
    else
    {
        for (int i = 1; i <= n; ++ i )
            for (int j = i + 1; j <= n; ++ j )
                g[i][j] = g[j][i] = get_dis(a[i], a[j]);
                
        printf("%.2lf\n", prim());
    }
    
    return 0;
}

kurskal的性质：
每次kruskal选择当前最小边更新时，本质是在建立连通块，初始每个点各自为连通块，数量为n，每次更新连通块的数量-1，更新n-1次选择了n-1条边后，连通块的数量为1，此时最小生成树构建完成

转换题意，找到一个最小d值，删除所有大于等于d的边后，剩下的连通块数量不超过k，两个连通块中的村庄用卫星通信通信
利用kruskal的性质，更新t次后， n − t = k n-t = k n−t=k时，表示已经建立了k个连通块，这些连通块中的最大边权为答案

// 跑个最小生成树，升序记录所有边权
// 若有k个卫星，选择第k大的边即可，因为k个卫星使得k个村庄可以直接通信
// k-1个最大边连接的存在用卫星，其他用发电设备通信
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;

typedef pair<int, int> PII;
const int N = 510, M = N * N / 2;
int p[N];
PII a[N];
bool st[N];
int n, k, cnt;

struct Edge
{
    int x, y;
    double w;
    bool operator<(const Edge& e)
    {
        return w < e.w;
    }
}edges[M];

double get_dis(PII a, PII b)
{
    int x = a.first - b.first, y = a.second - b.second;
    return sqrt(x * x + y * y);
}

int find(int x)
{
    if (x != p[x]) p[x] = find(p[x]);
    return p[x];
}

double kruskal()
{
    double res;
    int u = 0;
    sort(edges, edges + cnt);
    for (int i = 1; i <= n; ++ i) p[i] = i;
    for (int i = 0; i < cnt; ++ i )
    {
        if (n - u == k) break;
        auto t = edges[i];
        int x = t.x, y = t.y;
        double w = t.w;
        x = find(x), y = find(y);
        if (x != y)
        {
            u ++ ;
            res = w;
            p[x] = y;
        }
    }
    return res;
}

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; ++ i )
        scanf("%d%d", &a[i].first, &a[i].second);
    
    if (k >= n) puts("0.00");
    
    else
    {
        for (int i = 1; i <= n; ++ i )
            for (int j = i + 1; j <= n; ++ j )
                edges[cnt ++ ] = { i, j, get_dis(a[i], a[j])};
                
        printf("%.2lf\n", kruskal());
    }
    
    return 0;
}

debug：Edge中的w要用double存

最小生成树与完全图：346. 走廊泼水节

346. 走廊泼水节 - AcWing题库
image.png

如何合并完全图？开始时图中的每个点各自为一个集合，用集合合并的方式，保证合并后的集合为一个完全图
若集合a有x个点，b有y个点，要使得两集合合并后是个完全图（合并前两集合分别是完全图），就要将属于不同集合的点之间建一条边，总共需要建立xy条边

现在的问题是，将两个集合合并成完全图的边权为多大才能满足题意？
将树的每条边从小到大排序，每次合并当前枚举的边连接的两个集合，保证合并后的集合是一个完全图
由于要保证完全图的最小生成树唯一，所以要保证用来建立完全图的边权大于原生成树的边权

即当前枚举第i条边，这条边连接两个点 x i , y i x_i, y_i xi​,yi​，将 x i , y i x_i, y_i xi​,yi​所属的两个集合合并成完全图，需要在两个集合中的每个点之间建立一条边，并且该边的权值需要大于 w i w_i wi​

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 6010;
struct Edge
{
    int x, y, w;
    bool operator<(const Edge& e) const 
    {
        return w < e.w;
    }
}edges[N];
int p[N], sz[N];

int find(int x)
{
    if (x != p[x]) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    int T;
    scanf("%d", &T);
    while (T -- )
    {
        int n;
        scanf("%d", &n);
        for (int i = 0; i < n - 1; ++ i )
            scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);
        
        sort(edges, edges + n - 1);
        long long res = 0;
        for (int i = 1; i <= n; ++ i ) p[i] = i, sz[i] = 1;
        for (int i = 0; i < n - 1; ++ i )
        {
            auto t = edges[i];
            int x = find(t.x), y = find(t.y), w = t.w;
            if (x != y)
            {
                int n1 = sz[x], n2 = sz[y];
                p[x] = y;
                sz[y] += sz[x];
                res += (n1 * n2 - 1) * (w + 1);
            }
        }
        printf("%lld\n", res);
    }
    
    return 0;
}

debug：edges忘记了排序

次小生成树：1148. 秘密的牛奶运输

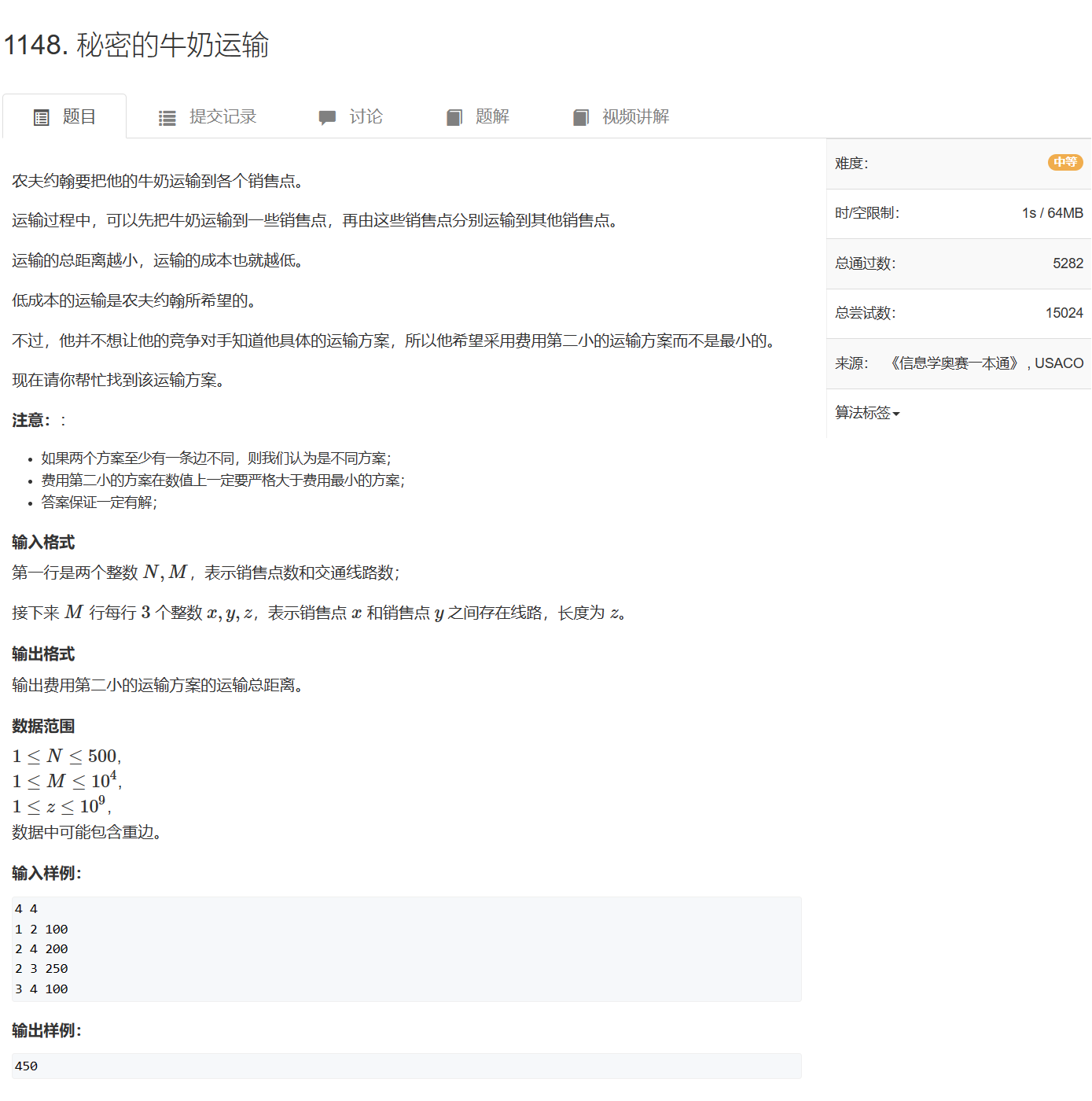
1148. 秘密的牛奶运输 - AcWing题库
image.png

次小生成树：
image.png

先求出最小生成树，删除最小生成树中的一条边
重复n-1次，得到的最小生成树就是次小生成树
注意：只能求出非严格次小生成树，即次小生成树的权值和可能等于最小生成树
时间复杂度 O ( m l n g m + n m ) O(mlngm + nm) O(mlngm+nm)

先求最小生成树，枚举不在树中的边，同时删除最小生成树（构成环）中的最大边，使得最终得到的图仍然是一颗树，次小生成树一定在这些树中

在生成树中任意添加一条边，必定构成环，此时需要在这个环路中删除一条边，使得该图再次成为一颗树，由于要保证权值和最小，所以要删除一条最大边
每次枚举非树边时，需要判断该边权值是否大于环的最大边，若大于则删除环中的最大值，此时能保证次小生成的权值和严格大于最小生成树
不过这种情况有一个特例，若非树边的权值等于最大边，当环中所有边的权值都等于最大边时，不更新次小生成树没有问题。若环中存在边权小于最大边的权值呢？此时可以删除这条次大的边，更新次小生成树。所以只通过判断非树边是否大于最大值将漏掉一些情况，导致少枚举次小生成树，最终导致答案的错误
因此，除了要维护两点间的最大边，还需要维护两点间的次大边，并且次大边需要严格小于最大边

若要生成非严格的次小生成树，只需要修改判断条件，在非树边的权值大于等于环的最大值时更新。多了权值相等的情况，所以删除的最大边可能和非树边权值相等，那么生成的次小生成树权值和就是相同的
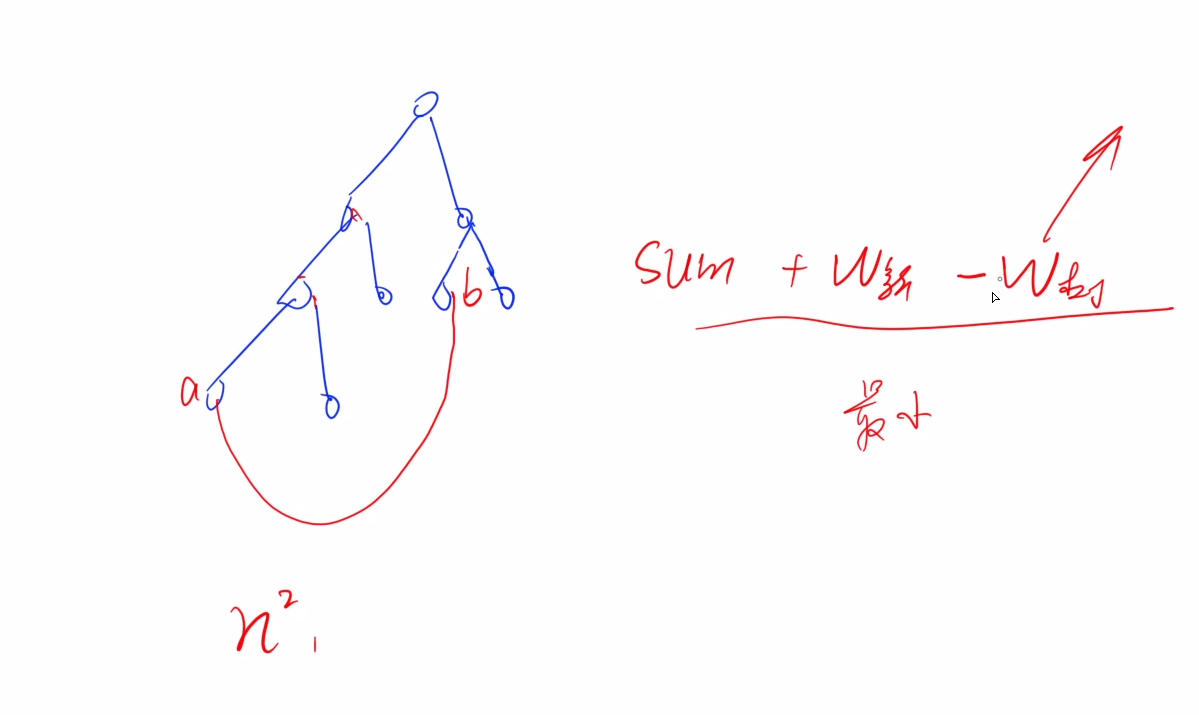
image.png

先预处理树中两点间的最大边，从根节点出发做一个dfs，每次都要 O ( n ) O(n) O(n)，时间复杂度是 O ( n 2 ) O(n^2) O(n2)
总的次小生成树的时间复杂度为 O ( m l n g m + n 2 + m ) O(mlngm + n^2 + m) O(mlngm+n2+m)

image.png
由于第二种求次小生成树的方式既可以求最小生成树也能求次小生成树，所以这里实现第二种
用两个二维数组表示最小生成树中任意两点的最大边与次大边

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

typedef long long LL;
const int N = 510, M = 1e4 + 10;
struct Edge
{
    int x, y, w;
    bool f;
    bool operator<(const Edge& e) const 
    {
        return w < e.w;
    }
}edges[M];

int p[N];
int h[N], e[M], ne[M], w[M], idx;
int dmax1[N][N], dmax2[N][N];
int n, m;

void add(int x, int y, int d)
{
    e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}

int find(int x)
{
    if (x != p[x]) p[x] = find(p[x]);
    return p[x];
}

// 走到x的最大边与次大边
void dfs(int x, int f, int d1, int d2, int xmax1[], int xmax2[])
{
    xmax1[x] = d1, xmax2[x] = d2;
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int y = e[i];
        if (y != f)
        {
            int t1 = d1, t2 = d2;
            if (w[i] > t1) t2 = t1, t1 = w[i];
            else if (w[i] < t1 && w[i] > t2) t2 = w[i];
            dfs(y, x, t1, t2, xmax1, xmax2);
        }
    }
}

LL kruskal()
{
    LL sum = 0;
    sort(edges, edges + m);
    for (int i = 1; i <= n; ++ i ) p[i] = i;
    for (int i = 0; i < m; ++ i )
    {
        auto t = edges[i];
        int x = t.x, y = t.y, w = t.w;
        int px = find(t.x), py = find(t.y);
        if (px != py)
        {
            sum += w;
            p[px] = py;
            add(x, y, w), add(y, x, w); // 存储最小生成树
            edges[i].f = true; // 树边
        }
    }
    return sum;
}

int main()
{
    memset(h, -1, sizeof(h));
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; ++ i ) scanf("%d%d%d", &edges[i].x, &edges[i].y, &edges[i].w);
    LL sum = kruskal();
    for (int i = 1; i <= n; ++ i ) dfs(i, -1, -1e9, -1e9, dmax1[i], dmax2[i]);
    LL res = 1e19;
    for (int i = 0; i < m; ++ i )
    {
        if (!edges[i].f)
        {
            int x = edges[i].x, y = edges[i].y, w = edges[i].w;
            if (w > dmax1[x][y]) res = min(res, sum - dmax1[x][y] + w);
            else if (w > dmax2[x][y]) res = min(res, sum - dmax2[x][y] + w);
        }
    }
    printf("%lld\n", res);
    return 0;
}

debug：构建最小生成树的同时，用邻接表存储最小生成树

auto t = edges[i];
int x = find(t.x), y = find(t.y), w = t.w;
if (x != y)
{
	sum += w;
	p[x] = y;
	add(x, y, w), add(y, x, w); // 存储最小生成树
	edges[i].f = true; // 树边
}

若这样写，构建的最小生成树是正确的，但是存储的最小生成树确实不正确的
因为x和y是边的两点所属的集合，不一定是边的两点，所以此时add无法正确保存最小生成树

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/841009.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

鸿蒙边缘计算网关正式开售

鸿蒙边缘计算网关正式开售

IDO-IPC3528鸿蒙边缘计算网关基于RK3568研发设计&#xff0c;采用22nm先进工艺制程&#xff0c;四核A55 CPU&#xff0c;主频高达2.0GHz&#xff0c;支持高达8GB高速LPDDR4&#xff0c;1T算力NPU&#xff0c;4K H.265/H264硬解码&#xff1b;视频输出接口HDMI2.0&#xff0c;双…
阅读更多...
JAVA SE -- 第十六天

JAVA SE -- 第十六天

&#xff08;全部来自“韩顺平教育”&#xff09; IO流 一、文件 是保存数据的地方 2、文件流 文件在程序中是以流的形式来操作 流&#xff1a;数据在数据源&#xff08;文件&#xff09;和程序&#xff08;内存&#xff09;之间经历的路径 输入流&#xff1a;数据从数据…
阅读更多...
UltraToolBars Crack,动画菜单和多种显示样式

UltraToolBars Crack,动画菜单和多种显示样式

UltraToolBars Crack,动画菜单和多种显示样式 创建模仿Microsoft Office 2000外观的健壮应用程序。 UltraToolBars包括11个用于创建可自定义工具栏的界面增强控件&#xff0c;包括&#xff1a;个性化菜单、弹出型工具栏、集成选项卡控件等。PictureRegion技术使表单和组件能够采…
阅读更多...
基于Java的新闻全文搜索引擎的设计与实现

基于Java的新闻全文搜索引擎的设计与实现

中文摘要 本文以学术研究为目的&#xff0c;针对新闻行业迫切需求和全文搜索引擎技术的优越性&#xff0c;设计并实现了一个针对新闻领域的全文搜索引擎。该搜索引擎通过Scrapy网络爬虫工具获取新闻页面&#xff0c;将新闻内容存储在分布式存储系统HBase中&#xff0c;并利用倒…
阅读更多...
Go 语言面试题（一）：基础语法

Go 语言面试题（一）：基础语法

文章目录 Q1 和 : 的区别&#xff1f;Q2 指针的作用&#xff1f;Q3 Go 允许多个返回值吗&#xff1f;Q4 Go 有异常类型吗&#xff1f;Q5 什么是协程&#xff08;Goroutine&#xff09;Q6 如何高效地拼接字符串Q7 什么是 rune 类型Q8 如何判断 map 中是否包含某个 key &#xf…
阅读更多...
STM32--GPIO

STM32--GPIO

文章目录 GPIO简介GPIO的基本结构GPIO位结构GPIO模式LED和蜂鸣器LED闪烁工程及程序原码代码&#xff1a; 蜂鸣器工程和程序原码代码 传感器光敏传感器控制蜂鸣器工程代码 GPIO简介 GPIO&#xff08;General Purpose Input Output&#xff09;是通用输入/输出口的简称。它是一种…
阅读更多...
利用el-button 画圆 ，通过border-radius ＞50% 就成圆形

利用el-button 画圆 ，通过border-radius ＞50% 就成圆形

<el-button type"danger" style"border-radius: 100%; height: 100px;width: 100px;" plain><span style"font-weight: bold;">工艺分析</span></el-button>通过border-radius >50% 就成圆形。 border-radius: 50% …
阅读更多...
STM32基础入门学习笔记：面包板 配件包扩展模块与编程

STM32基础入门学习笔记：面包板 配件包扩展模块与编程

文章目录&#xff1a; 一&#xff1a;阵列键盘 1.阵列键盘测试程序 KEYPAD4x4.h KEYPAD4x4.c main.c 2.键盘中断测试程序 NVIC.h NVIC.c main.c 二&#xff1a;舵机控制 1.延时函数驱动舵机程序 SG90.h SG90.c main.c 2.PWM(脉冲宽度调制 脉宽调制/占空比)驱动…
阅读更多...
极海APM32F003F6P6烧写问题解决记录

极海APM32F003F6P6烧写问题解决记录

工作中遇到的&#xff0c;折腾了好久&#xff0c;因为电脑重装过一遍系统&#xff0c;软件也都重新安装了&#xff0c;所以不知道之前的配置是什么&#xff0c;旧项目代码编译没问题&#xff0c;烧写时疯狂报错&#xff0c;用的是JLink。 keil版本v5.14 win10版本 JLink版本…
阅读更多...
PHP8的表达式-PHP8知识详解

PHP8的表达式-PHP8知识详解

表达式是 PHP 最重要的基石。在 PHP8中&#xff0c;几乎所写的任何东西都是一个表达式。简单但却最精确的定义一个表达式的方式就是"任何有值的东西"。 最基本的表达式形式是常量和变量。当键入"$a 5"&#xff0c;即将值"5"分配给变量 $a。&quo…
阅读更多...
RocketMQ Learning

RocketMQ Learning

一、RocketMQ RocketMQ的产品发展 MetaQ&#xff1a;2011年&#xff0c;阿里基于Kafka的设计使用Java完全重写并推出了MetaQ 1.0版本 。 2012年&#xff0c;阿里对MetaQ的存储进行了改进&#xff0c;推出MetaQ 2.0&#xff0c;同年阿里把Meta2.0从阿里内部开源出来&am…
阅读更多...
【Rust】Rust学习 第四章认识所有权

【Rust】Rust学习 第四章认识所有权

第四章认识所有权 所有权&#xff08;系统&#xff09;是 Rust 最为与众不同的特性&#xff0c;它让 Rust 无需垃圾回收&#xff08;garbage collector&#xff09;即可保障内存安全。因此&#xff0c;理解 Rust 中所有权如何工作是十分重要的。 4.1 所有权 所有运行的程序都…
阅读更多...
行业报告 | 大模型助力产业，持续推进人工智能科技创新

行业报告 | 大模型助力产业，持续推进人工智能科技创新

原创 | 文 BFT机器人 随着AI应用深入千行百业&#xff0c;大模型在多个产业领域发挥着积极的作用。英伟达、META、微软等多家公司纷纷宣布AI相关行业的合作和并购机会&#xff0c;加速研发各垂类领域AI大模型&#xff0c;算力需求有望持续向上。 英伟达&#xff1a;宣布5000万…
阅读更多...
[oeasy]python0081_[趣味拓展]ESC键进化历史_键盘演化过程_ANSI_控制序列_转义序列_CSI

[oeasy]python0081_[趣味拓展]ESC键进化历史_键盘演化过程_ANSI_控制序列_转义序列_CSI

光标位置 回忆上次内容 上次了解了 新的转义模式 \033 逃逸控制字符 escape 这个字符 让字符串 退出标准输出流进行控制信息的设置 可以设置 光标输出的位置 ASR33中的ALT MODE 是 今天的ESC键吗&#xff1f;&#xff1f;&#xff1f;&#xff1f;&#x1f914; 查询文档…
阅读更多...
2023-08-06 LeetCode每日一题（24. 两两交换链表中的节点）

2023-08-06 LeetCode每日一题（24. 两两交换链表中的节点）

2023-08-06每日一题 一、题目编号 24. 两两交换链表中的节点二、题目链接 点击跳转到题目位置 三、题目描述 给你一个链表&#xff0c;两两交换其中相邻的节点&#xff0c;并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题&#xff08;即&#xff0…
阅读更多...
MySQL索引原理以及SQL优化

MySQL索引原理以及SQL优化

文章目录 一、索引1.1 索引分类1.1.1 按数据结构分类1.1.2 按物理存储分类1.1.3 按列属性分类1.1.4 按列的个数索引 1.2 索引的代价1.3 索引的使用场景1.4 不使用索引的场景 二、索引的实现原理2.1 索引存储2.2 页2.3 InnoDB中的B树2.4 InnoDB的体系结构2.5 最左匹配原则2.6 覆…
阅读更多...
人工智能自然语言处理：抽取式文本分割（Text Segmentation）算法介绍总结，智能断句解决文本过长问题

人工智能自然语言处理：抽取式文本分割（Text Segmentation）算法介绍总结，智能断句解决文本过长问题

NLP专栏简介：数据增强、智能标注、意图识别算法|多分类算法、文本信息抽取、多模态信息抽取、可解释性分析、性能调优、模型压缩算法等 专栏详细介绍：NLP专栏简介：数据增强、智能标注、意图识别算法|多分类算法、文本信息抽取、多模态信息抽取、可解释性分析、性能调优、模型…
阅读更多...
快速修复应用程序中的问题的利器—— Android热修复

快速修复应用程序中的问题的利器—— Android热修复

热修复技术在Android开发中扮演着重要的角色&#xff0c;它可以帮助开发者在不需要重新发布应用程序的情况下修复已经上线的应用程序中的bug或者添加新的功能。 一、热修复是什么&#xff1f; 热修复&#xff08;HotFix&#xff09;是一种在运行时修复应用程序中的问题的技术…
阅读更多...
2023/08/05【网络课程总结】

2023/08/05【网络课程总结】

1. 查看git拉取记录 git reflog --dateiso|grep pull2. TCP/IP和OSI七层参考模型 3. DNS域名解析 4. 预检请求OPTIONS 5. 渲染进程的回流(reflow)和重绘(repaint) 6. V8解析JavaScript 7. CDN负载均衡的简单理解 8. 重学Ajax 重学Ajax满神 9. 对于XML的理解 大白话叙述XML是…
阅读更多...
图像 检测 - RetinaNet: Focal Loss for Dense Object Detection (arXiv 2018)

图像 检测 - RetinaNet: Focal Loss for Dense Object Detection (arXiv 2018)

图像 检测 - RetinaNet: Focal Loss for Dense Object Detection - 密集目标检测中的焦点损失&#xff08;arXiv 2018&#xff09; 摘要1. 引言2. 相关工作References 声明&#xff1a;此翻译仅为个人学习记录 文章信息 标题&#xff1a;RetinaNet: Focal Loss for Dense Obje…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023