FTP使用教程
目录
- 一.FTP简介
- 二.FTP搭建
- 三.FTP使用
一.FTP简介
FTP中文为文件传输协议,简称为文传协议。它也是一个应用程序,不同的操作系统有不同的FTP应用程序,这些应用程序都遵守同一种协议以传输文件。FTP主要的功能是“上传”和“下载”。端口号为21。
二.FTP搭建
详见搭建教程博客:https://danbaku.blog.csdn.net/article/details/131891480
三.FTP使用
- 在局域网内,客户机可以在文件路径栏里直接访问FTP服务器。鼠标拖拽其中文件,即可下载和上传。
命令:ftp://172.16.1.161:2121/

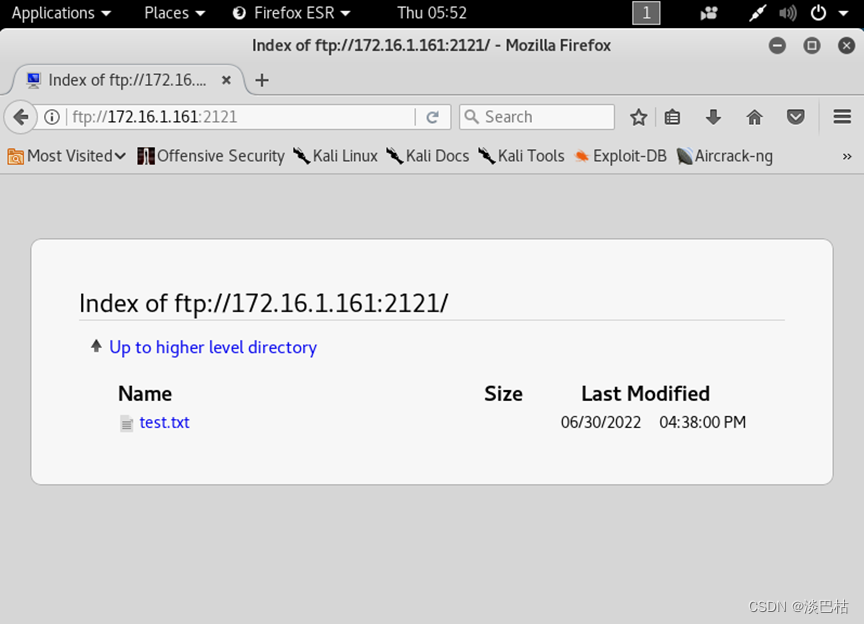
- 不同系统也可以访问FTP服务器。
命令:ftp://172.16.1.161:2121/
本篇博客为本人学习FTP时的详细笔记,如有错误之处,还望各位指正。
文章为原创,如要转载请注明出处