徐勇. 网络化多智能体系统的事件触发一致性研究[D].浙江大学,2020.DOI:10.27461/d.cnki.gzjdx.2020.001385.
文章目录
- 5 已知 DoS 攻击策略下多智能体系统的事件触发安全一致性分析
- 5.1 引言
- 5.2 数学模型与问题描述
- 5.3 控制器和事件触发条件的设计
- 5.5 数值仿真
- 程序 `Main.m`
- 程序 `Main_ET.m`
- 程序 `Main_ET_DoS.m`
- Ref
5 已知 DoS 攻击策略下多智能体系统的事件触发安全一致性分析
5.1 引言
5.2 数学模型与问题描述
在领航者-跟随者多智能体系统中,考虑跟随者智能体 i i i 的动态方程如下所示
x ˙ i ( t ) = A x i ( t ) + B u i ( t ) , i = 1 , ⋯ , N (5.1) \begin{aligned} \dot{x}_i(t) = A x_i(t) + B u_i(t), \quad i=1,\cdots,N \end{aligned} \tag{5.1} x˙i(t)=Axi(t)+Bui(t),i=1,⋯,N(5.1)
其中,
x
i
(
t
)
∈
R
n
\red{x_i(t)} \in \R^n
xi(t)∈Rn 表示状态,
u
i
(
t
)
∈
R
n
\red{u_i(t)} \in \R^n
ui(t)∈Rn 表示输入。
假设智能体 0 是领航者,其动态方程为
x ˙ 0 ( t ) = A x 0 ( t ) (5.2) \begin{aligned} \dot{x}_0(t) = A x_0(t) \end{aligned} \tag{5.2} x˙0(t)=Ax0(t)(5.2)
其中,
x
0
(
t
)
∈
R
n
\red{x_0(t)} \in \R^n
x0(t)∈Rn 表示状态。
x ˙ 01 = x 02 x ˙ 02 = 0.15 ∗ x 01 − x 02 (自己推) \begin{aligned} \dot{x}_{01} &= x_{02} \\ \dot{x}_{02} &= 0.15 * x_{01} - x_{02} \end{aligned} \tag{自己推} x˙01x˙02=x02=0.15∗x01−x02(自己推)
5.3 控制器和事件触发条件的设计
如下事件触发控制协议
u i ( t ) = γ K ( S i ( t k i ) + a i 0 Z i ( t k i ) ) , t ∈ [ t k i , t k + 1 i ) (5.3) \begin{aligned} u_i(t) = \gamma K( S_i(t^i_k)+a_{i0} Z_i(t^i_k) ), \quad t \in [t^i_k, t^i_{k+1}) \end{aligned} \tag{5.3} ui(t)=γK(Si(tki)+ai0Zi(tki)),t∈[tki,tk+1i)(5.3)
其中,
γ
>
0
\red{\gamma} > 0
γ>0,
S i ( t ) = ∑ j ∈ N i a i j ( x j ( t ) − x i ( t ) ) Z i ( t ) = x 0 ( t ) − x i ( t ) (5.4) \begin{aligned} S_i(t) &= \sum_{j \in N_i} a_{ij} (x_j(t) - x_i(t)) \\ Z_i(t) &= x_0(t) - x_i(t) \end{aligned} \tag{5.4} Si(t)Zi(t)=j∈Ni∑aij(xj(t)−xi(t))=x0(t)−xi(t)(5.4)
t k i \red{t^i_k} tki 表示智能体 i i i 的触发时刻并且属于触发时刻集合 { t 0 i , t 1 i , ⋯ , ∞ } \{t^i_0, t^i_1, \cdots, \infty\} {t0i,t1i,⋯,∞}。在触发时刻,智能体 i i i 需要采集它的状态和它邻居的状态去更新控制输入。
定义两个状态测量误差 e i ( t ) \red{e_i(t)} ei(t) 和 e i 0 ( t ) \red{e_{i0}(t)} ei0(t) 如下所示
e i ( t ) = S i ( t k i ) − S i ( t ) e i 0 ( t ) = Z i ( t k i ) − Z i ( t ) (5.5) \begin{aligned} e_i(t) &= S_i(t^i_k) - S_i(t) \\ e_{i0}(t) &= Z_i(t^i_k) - Z_i(t) \end{aligned} \tag{5.5} ei(t)ei0(t)=Si(tki)−Si(t)=Zi(tki)−Zi(t)(5.5)
根据状态测量误差 (5.5) 设计事件触发函数 f ( e i ( t ) , e i 0 ( t ) , t ) f(e_i(t), e_{i0}(t), t) f(ei(t),ei0(t),t) 如下所示
t k + 1 i = inf { t k i ∣ f ( e i ( t ) , e i 0 ( t ) , t ) = ∥ e i ( t ) ∥ 2 + a i 0 2 ∥ e i 0 ( t ) ∥ 2 ≤ ϑ i 2 Θ i 2 ( t ) } (5.7) \begin{aligned} t^i_{k+1} = \inf \{ t^i_k | f(e_i(t), e_{i0}(t), t) = \|e_i(t)\|^2 + a_{i0}^2 \|e_{i0}(t)\|^2 \le \vartheta^2_i \Theta^2_i(t) \} \end{aligned} \tag{5.7} tk+1i=inf{tki∣f(ei(t),ei0(t),t)=∥ei(t)∥2+ai02∥ei0(t)∥2≤ϑi2Θi2(t)}(5.7)
其中
Θ
i
(
t
)
=
∥
S
i
(
t
)
∥
+
a
i
0
∥
Z
i
(
t
)
∥
\red{\Theta_i(t)} = \|S_i(t)\| + a_{i0} \|Z_i(t)\|
Θi(t)=∥Si(t)∥+ai0∥Zi(t)∥,
β
>
2
∥
Q
B
B
T
Q
∥
\red{\beta} > 2\|QBB^\text{T} Q\|
β>2∥QBBTQ∥,
σ
i
∈
(
0
,
1
)
\red{\sigma_i} \in (0,1)
σi∈(0,1) 和选取足够大的参数
δ
\red{\delta}
δ 使得
ϑ i = σ i β − 2 ∥ Q B B T Q ∥ γ δ − 1 ( 4 ∣ N i ∣ 2 + 2 a i 0 2 ) ∥ Q B B T Q ∥ > 0 \vartheta_i = \sqrt{\sigma_i \frac{\beta - 2\|QBB^\text{T} Q\| \gamma \delta^{-1} }{(4|N_i|^2+2a_{i0}^2)\|QBB^\text{T} Q\|}} > 0 ϑi=σi(4∣Ni∣2+2ai02)∥QBBTQ∥β−2∥QBBTQ∥γδ−1>0
成立。
5.5 数值仿真

程序 Main.m
文中给的参数我做不出来和论文一样的效果,
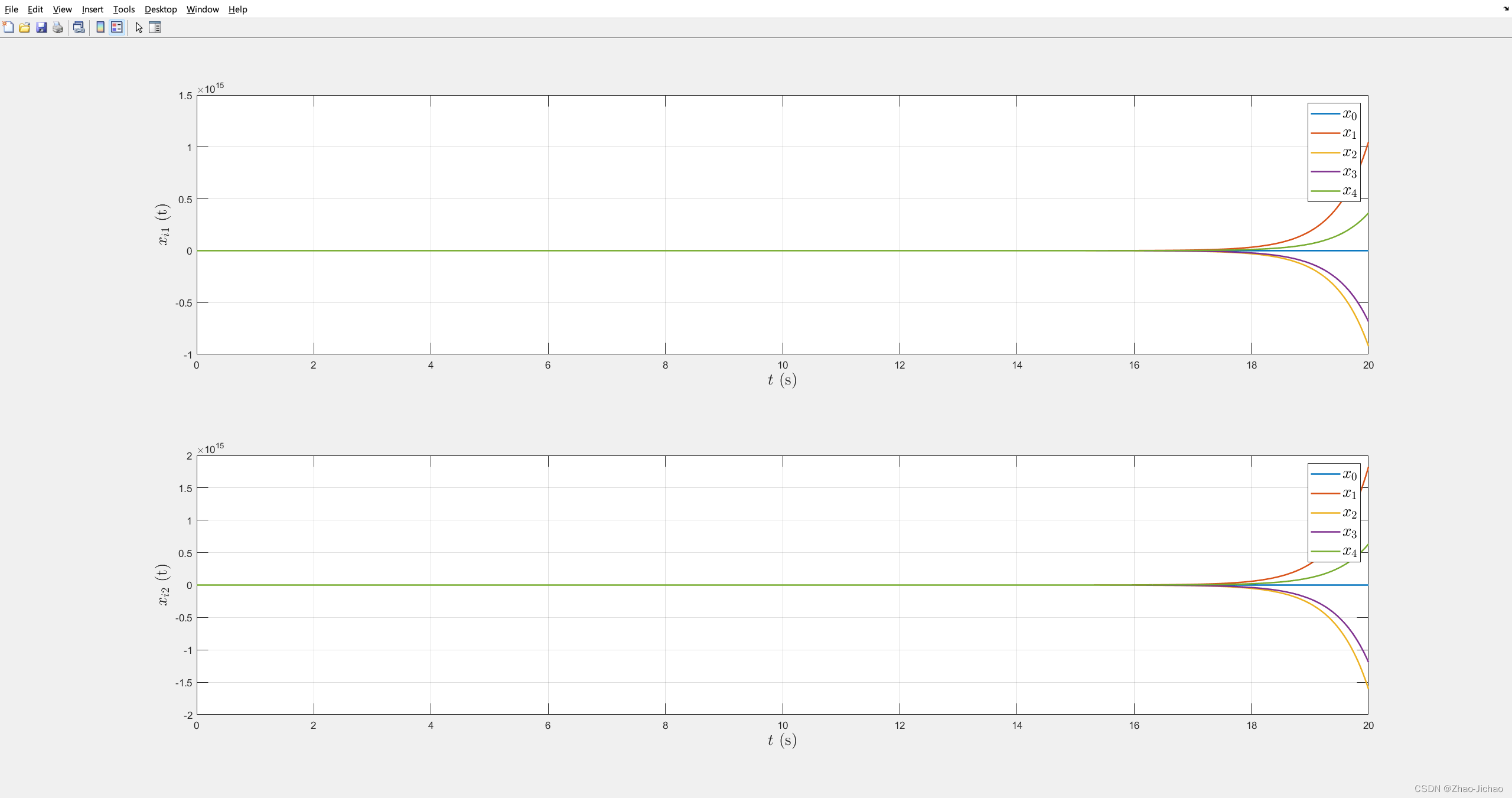
调整后才有效果:
- 调整了 A A A 矩阵
- 调整了参数 γ \gamma γ
得到了类似的效果,然后就按照这个效果往下继续走了。
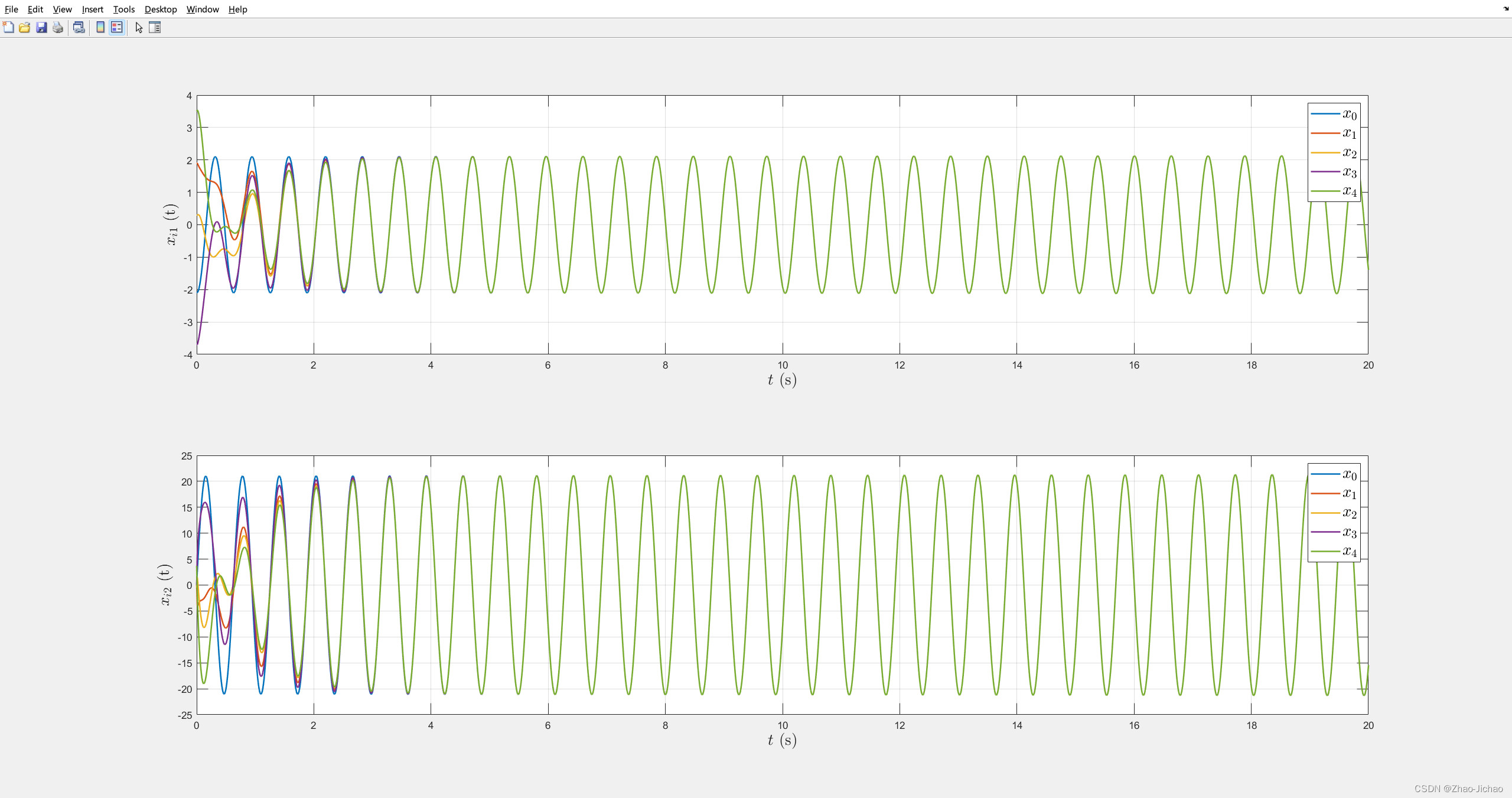
程序 Main_ET.m
然后加入事件触发机制,效果如下:
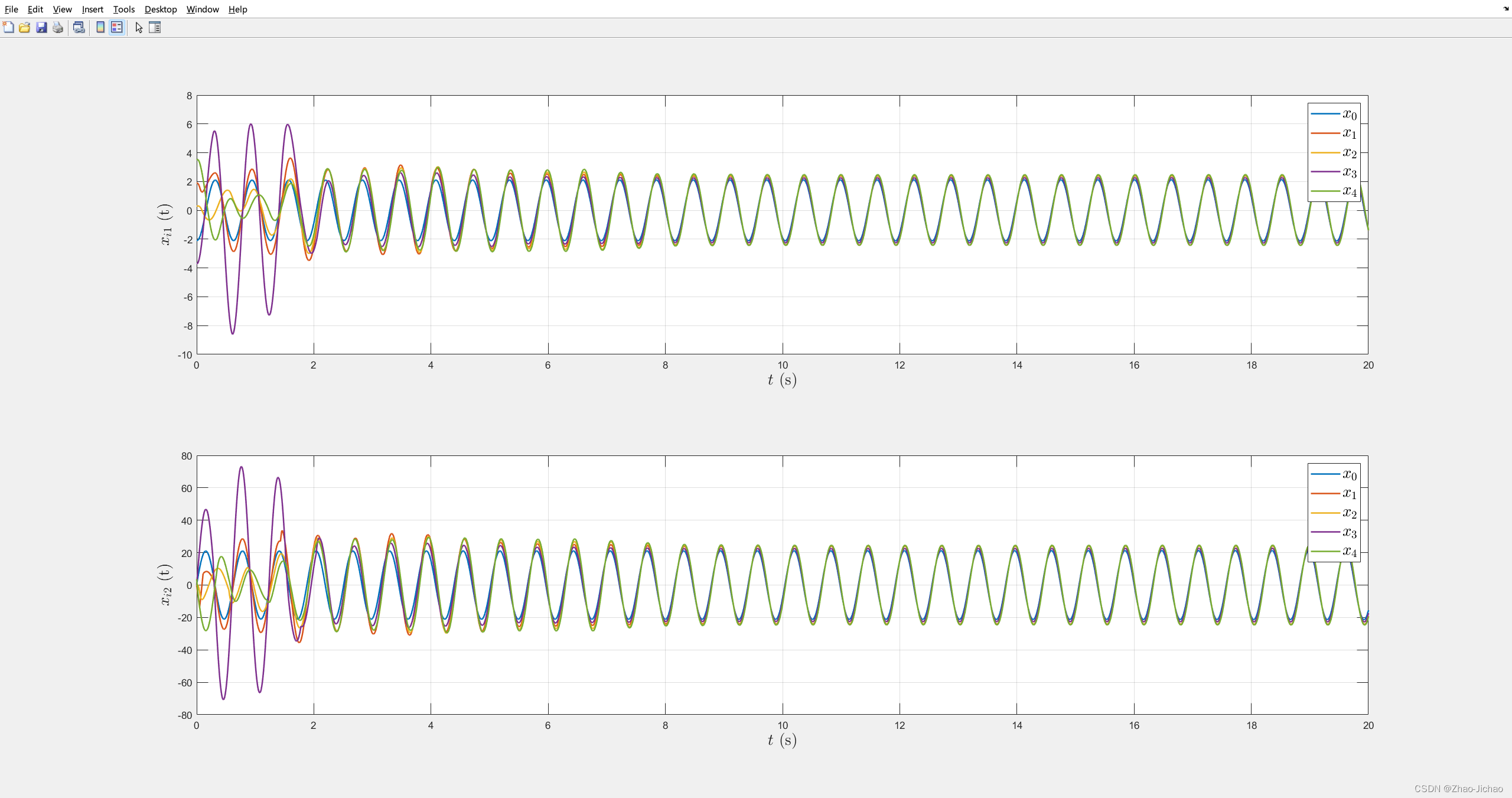
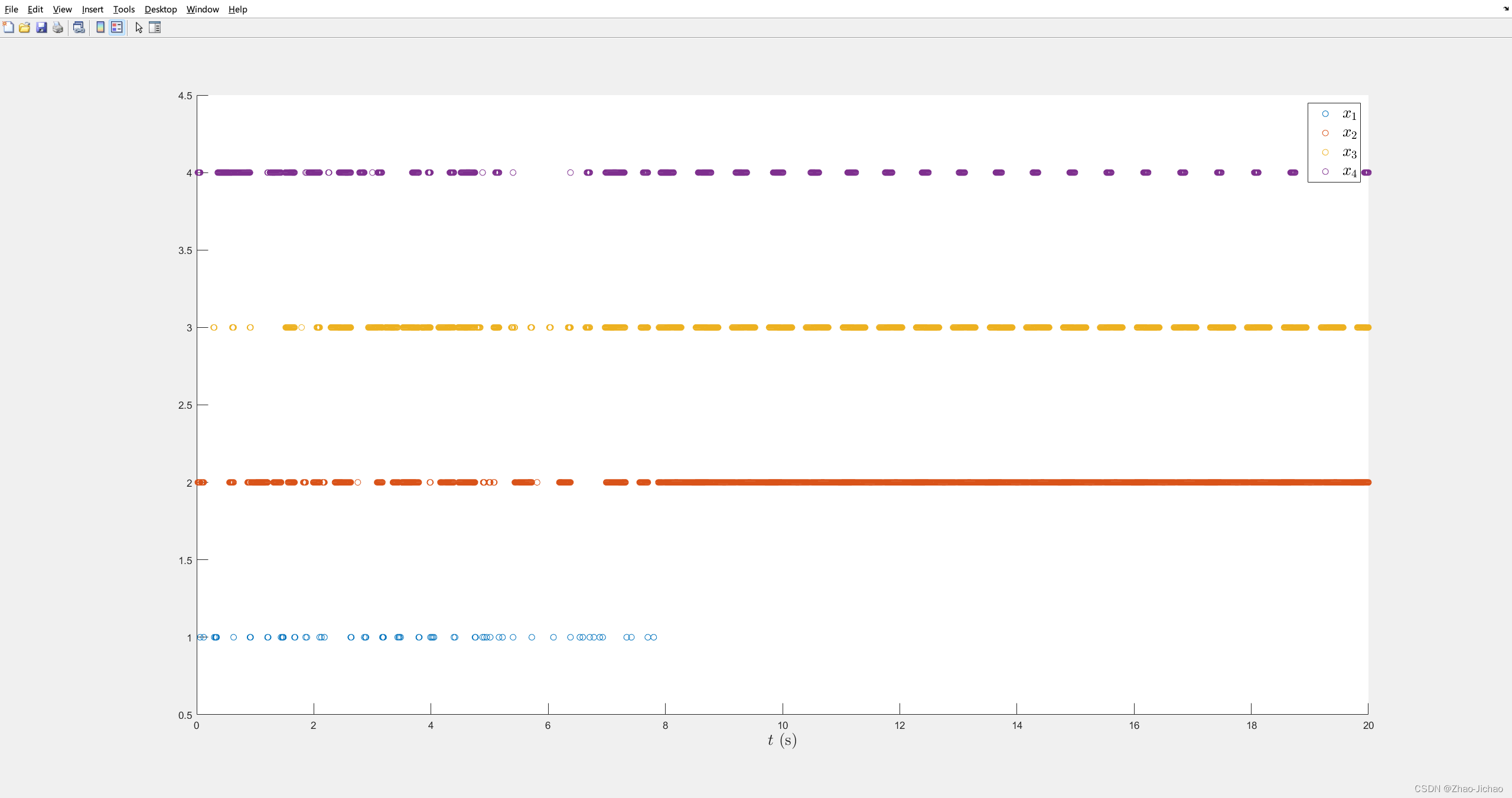
程序 Main_ET_DoS.m
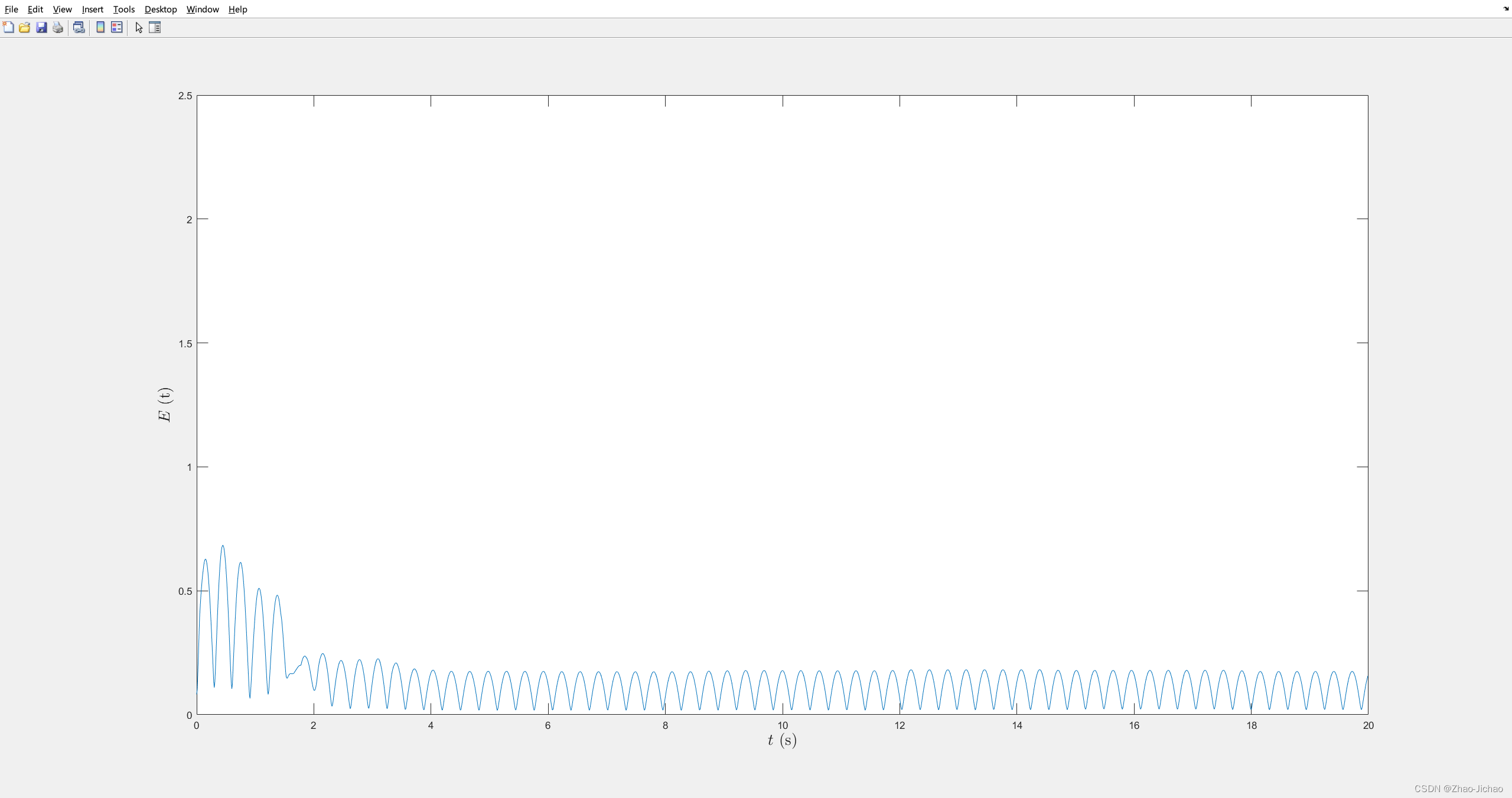
然后加入 DoS 攻击机制,效果如下:

虽然事件触发效果有点问题,但是我反复核对了 DoS 攻击,实现的机制是没错的。并且由于之前这个文章的参数就不对,所以再调试下去也没太大意义了。
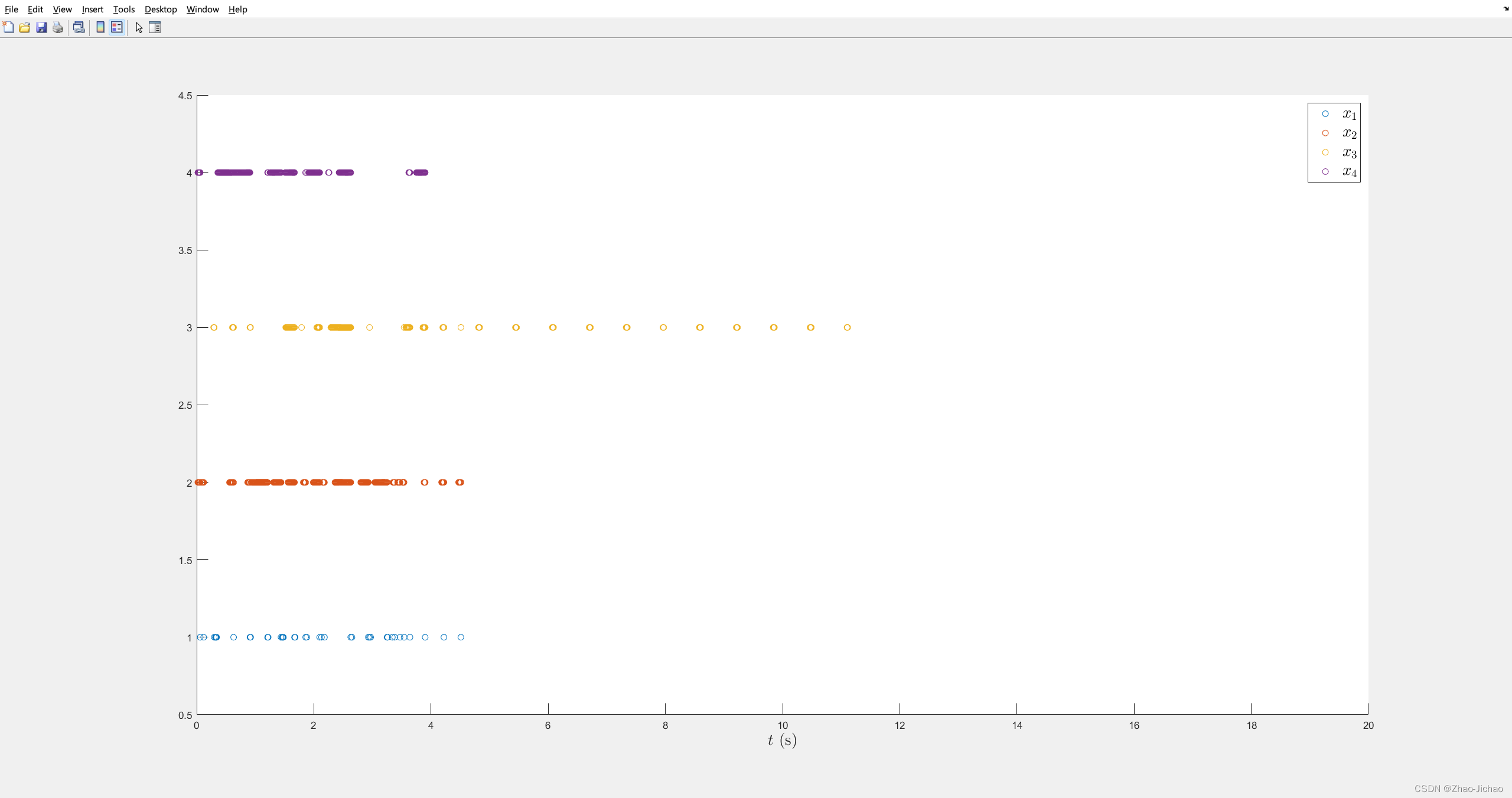

包括误差也是,我反复确认了程序,使用的方法是和论文一致的,虽然效果一般,但是和理论上是说的过去的。因为状态效果就是一个一直在跟随领航者,所以误差最后也是一个振荡的,这是合理的。