2023牛客暑期多校训练营6-A Tree

https://ac.nowcoder.com/acm/contest/57360/A

题意

解题思路

最大价值和这个数据范围，一眼$dp$。

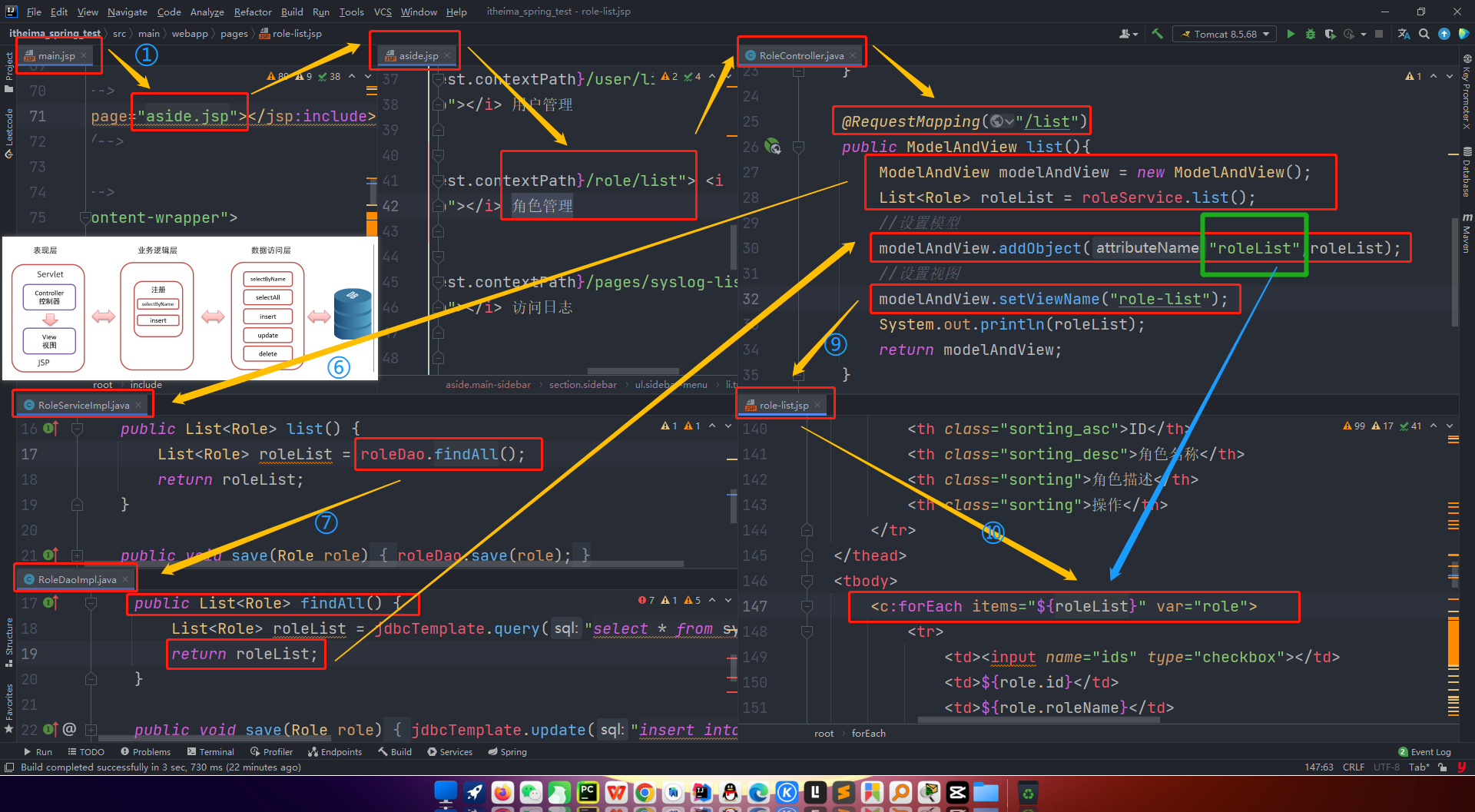
直接在树上并不好处理，问题是如何有效转化、处理$x,y$之间的最短路径上的最大边权值。这里用到了$kruskal重构树$，$kruskal算法$是一种贪心地求最小生成树的算法，本题所用算法参照了该算法的思路，将一张无向图的边按边权排序，一次取用，不同的是，我们将每条边转化为带有点权的虚点，任意两点由虚点连接，而原图上的点均为叶子结点，如图：

一条边的两个端点将祖先连在一起，可以用并查集实现。

根据这种树的特殊性质，其虚点的权值自上而下减少，原图上两个点之间的最短路径上的最大权值即为该图上两点最近公共祖先的点权。此时可以进行树形$dp$了！

设$d{p}_{x,b}$表示以$x$为根的字数内黑点个数为$b$的贡献最大值，对于原图上任意边，其贡献值为
$(W_1\times B_2+W_2\times B_1)\times k$，推理得：
$$\begin{gathered} d{p}_{x,b}=Ma{x}_{b-s{z}_r\le b_1\le min(b,s{z}_l)}(d{p}_{l,b_1}+d{p}_{r,b-b_1}+ \\ {k}_x\times (b_1(左子树黑点个数)\times (s{z}_r-b+b_1)(右子树白点个数)+ \\ (s{z}_l-b_1)(左子树白点个数)\times (b-b_1)(右子树黑点个数))) \end{gathered}$$
对于叶子结点$leaf$：
$$\begin{gathered} d{p}_{leaf,a[leaf]\oplus 1}=-cos{t}_{leaf} \\ d{p}_{leaf,a[leaf]}=0 \end{gathered}$$

注意内存与结果大小，$dp$数组可以用$vector<longlong>$。

代码

#include<bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N=6005;
int n,a[N],c[N],f[N],m,sz[N],b[N];
pair<int,int>e[N];
struct node{
	int u,v,w;
}p[N];
vector<ll> dp[N];
bool cmp(node a,node b){
	return a.w<b.w;
}
int sf(int x){
	if(f[x]==x)return x;
	return f[x]=sf(f[x]);
}
void dfs(int u){
	
	if(u<=n){
        dp[u][a[u]^1]=-c[u];
		dp[u][a[u]]=0;
		sz[u]=1;
		return;
	}
	int l=e[u].first,r=e[u].second;
	dfs(l),dfs(r);
	sz[u]=sz[l]+sz[r];
	dp[u]=vector<ll>(sz[u]+1,-0x3f3f3f3f3f3f);
	if(sz[l]>sz[r])swap(l,r);
	for(int x=0;x<=sz[u];x++)
	for(int i=max(0,x-sz[r]);i<=min(sz[l],x);i++){
		dp[u][x]=max(dp[u][x],dp[l][i]+dp[r][x-i]+b[u]*(i*(sz[r]-x+i)+(sz[l]-i)*(x-i)));
	}
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i],dp[i].resize(2);
	for(int i=1;i<=2*n;i++)f[i]=i;
	for(int i=1;i<=n;i++)cin>>c[i];
	for(int i=1;i<n;i++){
		int u,v,w;
		cin>>u>>v>>w;
		p[i].u=u,p[i].v=v,p[i].w=w;
	}
	sort(p+1,p+n,cmp);
	m=n;
	for(int i=1;i<n;i++){
		int u=p[i].u,v=p[i].v,w=p[i].w;
		if(sf(u)==sf(v))continue;
		++m;
		b[m]=w;
		e[m].first=sf(u),e[m].second=sf(v);
		f[sf(u)]=f[sf(v)]=m;
	}
	dfs(sf(1));
	ll ans=0;
	for(int i=0;i<=n;i++){
		ans=max(ans,dp[sf(1)][i]);
	}
	cout<<ans;
}