前言

删除字符串中的所有相邻重复项
逆波兰表达式求值
滑动窗口最大值
前 K 个高频元素
数组中的第K个最大元素

一、删除字符串中的所有相邻重复项（力扣047）

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
在这里插入图片描述
解题思路：
利用栈，首先将第一个元素放入栈中，然后遍历下一个元素时，判断是否和栈顶元素相同，相同则将栈顶元素弹出，不同则将该元素入栈即可。

class Solution {
    public String removeDuplicates(String s) {
        ArrayDeque<Character> deque = new ArrayDeque<>();
        char[] chars = s.toCharArray();
        if(chars.length==0){
            return "";
        }
        for(int i = 0;i<chars.length;i++){
            char ch = chars[i];
            if(deque.isEmpty()||ch!=deque.peek()){
                deque.push(ch);
            }else{
                deque.pop();
            } 
        }
        String str="";
        while(!deque.isEmpty()){
            str = deque.pop()+str;
        }
    return str;
    }
}

在这里插入图片描述

二、逆波兰表达式求值（力扣150）

根据逆波兰表示法，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

注意两个整数之间的除法只保留整数部分。

可以保证给定的逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。
在这里插入图片描述
思路：
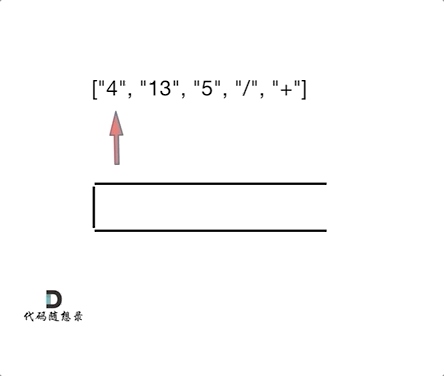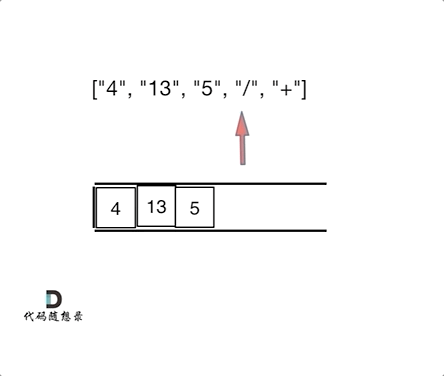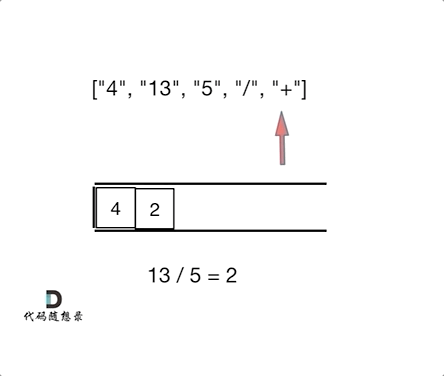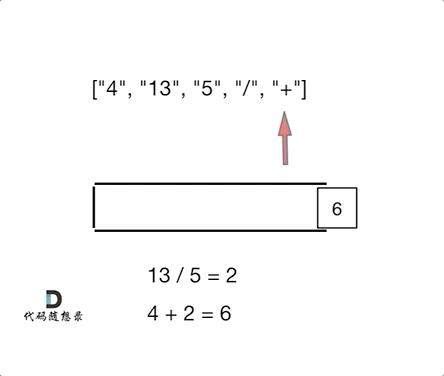
后缀表达式请添加图片描述

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> deque = new LinkedList<>();
        for(String s:tokens){
            if("+".equals(s)){
                deque.push(deque.pop()+deque.pop());
            }else if("-".equals(s)){
                deque.push(-deque.pop()+deque.pop());
            }else if("*".equals(s)){
                deque.push(deque.pop()*deque.pop());
            }else if("/".equals(s)){
                int temp1 = deque.pop();
                int temp2 = deque.pop();
                deque.push(temp2/temp1);
            }else{
                deque.push(Integer.valueOf(s));
            }
        }
        return deque.pop();
    }
}

在这里插入图片描述

三、滑动窗口最大值（力扣239）

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。
在这里插入图片描述
请添加图片描述

//自定义数组
class MyQueue{
    Deque<Integer> deque = new LinkedList<>();
    void poll(int val){
        if(!deque.isEmpty() && val == deque.peek()){
            deque.poll();
        }
    }
    //deque.getLast()入口处的元素
    void add(int val){
        while(!deque.isEmpty() && val>deque.getLast()){
            deque.removeLast();
        }
        deque.add(val);
    }
    //队列队顶元素始终为最大值 
    int peek() {
        return deque.peek();
    }
}
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length==1){
            return nums;
        }
        int len = nums.length - k + 1;
        //存放结果的数组
        int[] res = new int[len];
        int num=0;
        MyQueue myQueue = new MyQueue();
        for(int i=0;i<k;i++){
            myQueue.add(nums[i]);
        }
        res[num++] = myQueue.peek();
        for(int i = k;i<nums.length;i++){
            myQueue.poll(nums[i-k]);
            myQueue.add(nums[i]);
            res[num++]=myQueue.peek();
        }
        return res;
    }
}

在这里插入图片描述

四、前 K 个高频元素（力扣347）

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按任意顺序返回答案。
在这里插入图片描述
思路：
利用map记录每一个数出现的次数只取前k个频率最大的，利用堆排解决即可。注意：用的一定是小顶堆（优先级队列）这个堆只维护k个元素，如果是大顶堆则需要对所有元素进行排序依次从队头弹出k个,就是出现频率前k高的元素

//出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)
PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2)->pair1[1]-pair2[1]);
//出现次数按从队头到队尾的顺序是从大到小排,出现次数最多的在队头(相当于大顶堆)
PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2)->pair2[1]-pair1[1]);

小顶堆：

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int num:nums){
            map.put(num,map.getOrDefault(num,0)+1);
        }
        //小顶堆实现：
        //出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2)->pair1[1]-pair2[1]);
        //小顶堆只需要维持k个元素有序即可
        for(Map.Entry<Integer,Integer> entry:map.entrySet()){
            if(pq.size()<k){
                pq.add(new int[]{entry.getKey(),entry.getValue()});
            }else{
                if(entry.getValue()>pq.peek()[1]){//当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)
                    pq.poll();
                    pq.add(new int[]{entry.getKey(),entry.getValue()});
                }
            }
        }
        int[] ans = new int[k];
        for(int i=k-1;i>=0;i--){
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
}

大顶堆：

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int num:nums){
            map.put(num,map.getOrDefault(num,0)+1);
        }
        //小顶堆实现：
        //出现次数按从队头到队尾的顺序是从大到小排,出现次数最高的在队头(相当于大顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2)->pair2[1]-pair1[1]);
        //大顶堆需要对所有元素进行排序
        for(Map.Entry<Integer,Integer> entry:map.entrySet()){
            pq.add(new int[]{entry.getKey(),entry.getValue()});
        }
        int[] ans = new int[k];
        for(int i=0;i<k;i++){
            ans[i] = pq.poll()[0];//依次从队头弹出k个,就是出现频率前k高的元素
        }
        return ans;
    }
}

在这里插入图片描述

五、数组中的第K个最大元素（力扣215）

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
在这里插入图片描述
大顶堆

class Solution {
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> pq = new PriorityQueue<>((pair1,pair2)->pair2-pair1);
        for(int num:nums){
            pq.add(num);
        }
        int[] res = new int[k];
        for(int i=0;i<k;i++){
            res[i] = pq.poll();
        }
        return res[k-1];
    }
}