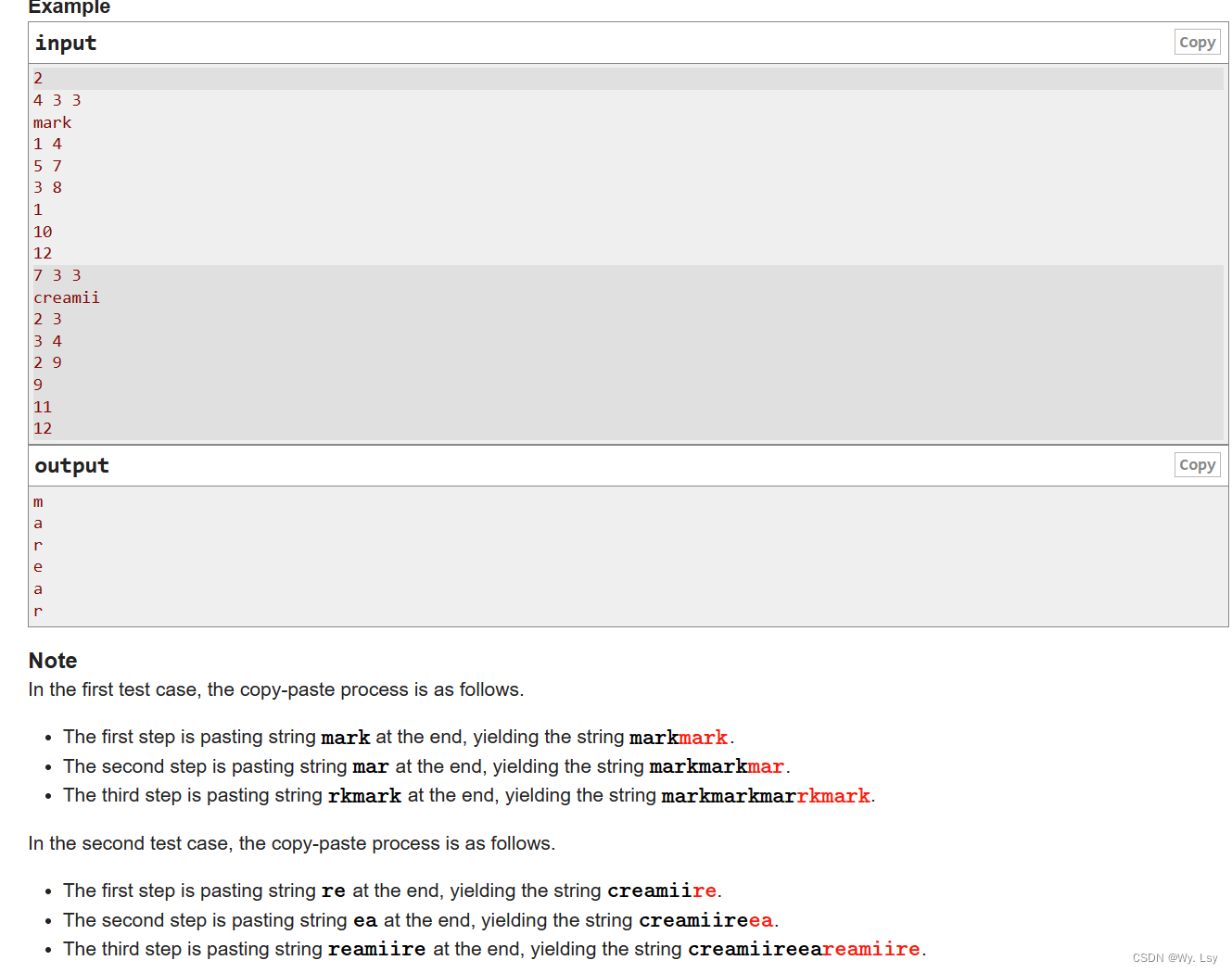
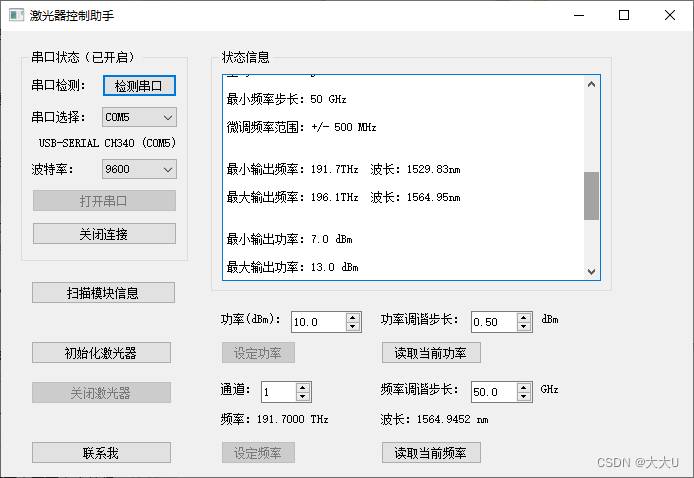
题目描述：
继续更新
再更问题三
继续更新第一问、第四问
1.2 问题重述
在制定电动车调度方案时，必须考虑充、换电池的时间成本，从而提出了新
的车辆运输选址及调度问题。
1） 已知自动驾驶电动物料车在取料点 P 和卸货点 D 之间往复运送物料，
通过建立数学规划模型，在 P 点和 D 点之间确定一个换电站选址及调
度方案，以满足资源约束与电池运行方式为约束条件，实现极大化制
定时间段内运送物料量的目标。基于附录中的数据求解规划模型得到
换电站的位置，并求得 1000 小时内所运输的物料量，所使用车辆、
电池组数量和车辆及其电池组的具体调度方案。
2） 在基于问题 1 其他条件与任务不变的情况下，将建站条件更改为“在
P 点与 D 点之间每个方向分别确定一个换电站位置”。
3） 在考虑峰谷电价、购置电池组、建设充、换电站等成本的基础上，制
定被整每日最低运输量、3 年结算周期投资运行成本最低的建站及电
池组调度方案。根据附录所给的数据（缺考的数据自行补充），给出
具体算例。
4） 对多个取料点、单个卸货点，研究上述换电站选址及车辆-电池组调
度问题。
二、 问题分析
基于动态规划的电动物料车换电站选址及调度方案
摘要
5.1.1
在温室效应逐年加剧的状态下，环保的自动驾驶电动车是发展趋势。本文
通过建立数学规划模型，分析了自动驾驶物料电动车在取料点与卸货点之间循环
往复运送物料耗电情况，并在极大化指定时间段内运送物料量的情况下给出换电
站的选址及调度方案。该问题的研究对电动汽车的推广具有重要意义，并能有效
节省时间与资源，提高运输物料的效率。
本文首先对附录数据进行分析，可知车道上最多可跑 98 辆车，每隔 12 秒发
一次车，在看周期的情况下，载货状态跑一趟消耗 5%电量，空载状态跑一趟大
约消耗 3.33%电量。往返 9 次消耗 75%的电量。运输车换电均需花费 2 分钟，与
完成一次装卸货时间相同，换电站内900组电池组共可满足150辆车的换电需求。
针对问题一，首先将极大化制定时间段内运送物料量问题转化为保持路上拥
有在约束条件下最大的车辆数，尽可能减少因换电和装卸货所浪费的时间，即使
得到达 D 点的次数最多。因此，以换电站与 P 点之间的距离
𝑋?
为决策变量，以
资源约束与电池运行方式为约束条件，建立以指定时间段内到达 D 点次数最多为
目标的目标函数。通过 Python 使用模拟退火算法，求得最优解 X 的值为 5.5。
得出换电站距离为5.5KM时后面的问题就迎刃而解，
1： 所使用的车辆数应该为118辆（实际根据你的假设可能略有出入），
原因是第一辆车经过程 1，换电过程花费的 2 分
钟中，A 处继续派出了 10 辆车。第一辆车经过程 2 最后到达 A 点处时，为了节
省时间，继续在 A 处派出 10 辆车，并开始循环，
2： 所使用的电池组数为
108 × 6 = 648
组，原因是第一辆车与第 98 辆车经过
程 1 到达 B 点处换电需要 98 辆车所要的电池组数，而有上述分析知，第一辆车
经过程 2 之后，第 99 辆车已经过程 1 开始在 B 点处充电了，之前新增的 10 辆车
也需充电，因此共需要为 108 辆车提供换电池组，
5.1.2 模型建立
这是一个规划类问题，可用线性规划模型来进行求解。规划模型的要素：决
策变量，目标函数，约束条件。
本题的决策变量是换电站的位置，假设换电站位置距离 P 点
𝑋?
，则它到 D
点的距离为
𝑋?
。我们还需要一系列的调度方案。根据文中的信息，实际上，我
们还需要根据的取值范围来进一步确定我们的规划模型。
运输车的路程情况如下图：
图
1
双向同址下换电站运输车的路程情况
由于该换电站是一个双向同址，沿 D 到 P 方向时，记该换电站为 A；沿 P 到
D 方向时，记该换电站为 B。
已知一辆车从发货地满电量出发，最后到换电站换电也是满电的，之后的每
一次满电状态均是从换电站出发的，于是我们可以假设运输车辆都是从换电站出
发的。
满足约束的方程组如下：
83.3% + 5?6 % ≤ 90%
83.3% + 56 10 − ? % ≤ 90%
0 ≤ ? ≤ 10
220 + 2? = 2 + 220 + 2(10 − ?)
?表示X变量显示不出来
要具体了解可以 关注后 私信我
下面是第一问部分源码
import random #
导⼊模块
import pandas as pd
import numpy as np import matplotlib.pyplot as plt from datetime import datetime From sympy import symbols,solve,linsolve
x=symbols('x')
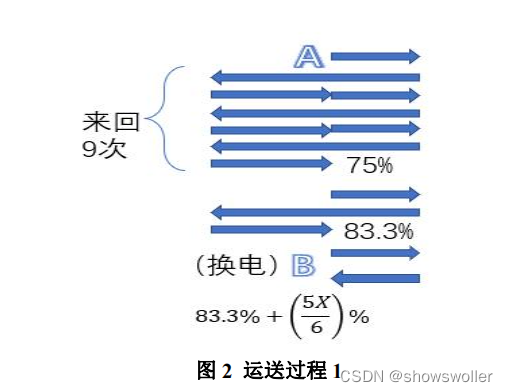
f1=(5/6)*x*0.01+0.833-0.90
print(solve([f1<=0,f2<=0]))
f3=4*x+200-222 #求解等式
print(solve(4*x+200-222,x)) #
⼦程序：定义优化问题的⽬标函数 def cal_Energy(X, nVar, mk): #
m(k)：惩罚因⼦，随迭代次数 k 逐渐增 ⼤
p1 = (max(0, 6*X[0]+5*X[1]-60))**2
p2 = (max(0, 10*X[0]+20*X[1]-150))**2 fx = -(10*X[0]+9*X[1]) return fx+mk*(p1+p2) # ⼦程序：模拟退⽕算法的参数设置
def ParameterSetting(): cName = "funcOpt" #
定义问题名称 YouCans, XUPT nVar = 2 # 给定⾃变量数量，
y=f(x1,..xn) xMin = [0, 0] xMax = [8, 8] tInitial = 100.0 tFinal = 1 13
alfa = 0.98 meanMarkov = 100 #
Markov 链长度，也即内循环运⾏次数 scale = 0.5 #
定义搜索步长，可以设为固定值或逐渐缩⼩ return cName, nVar, xMin, xMax, tInitial, tFinal, alfa, meanMarkov, scale# 模拟退⽕算法
def OptimizationSSA(nVar,xMin,xMax,tInitial,tFinal,alfa,meanMarkov,scale) :
# ====== 初始化随机数发⽣器 ====== randseed = random.randint(1, 100) random.seed(randseed) # 随机数发⽣器设置种⼦，也可以设为指定整数 # ====== 随机产⽣优化问题的初始解 ====== xInitial = np.zeros((nVar)) # 初始化，
创建数组
for v in range(nVar): # xInitial[v] = random.uniform(xMin[v], xMax[v]) #
产⽣ [xMin, xMax] 范围的随机实数 xInitial[v] = random.randint(xMin[v], xMax[v]) #
产⽣ [xMin, xMax] 范围的随机整数 #
调⽤⼦函数 cal_Energy 计算当前解的⽬标函数值 fxInitial = cal_Energy(xInitial, nVar, 1)
# m(k)：惩罚因⼦，初值为 1
# ====== 模拟退⽕算法初始化 ====== xNew = np.zeros((nVar)) #
初始化，创建数组 xNow = np.zeros((nVar)) # 初
始化，创建数组 xBest = np.zeros((nVar)) #
初始化，创建数组 xNow[:] = xInitial[:] #
初始化当前解，将初始解置为当前解 xBest[:] = xInitial[:] # 初始化最优解，将当前解置为最优解 fxNow = fxInitial # 将初始解的⽬标函数置为当前值误差因子检验部分代码如下：
误差因子分析：
load ('text.mat');
X=data;
z=zscore(X)
%数据标准化
M=cov(z)
[V,D]=eig(M); d=diag(D); ）
eig1=sort(d,'descend')
v=fliplr(V)
S=0; i=0;
while S/sum(eig1)<0.85 i=i+1;
S=S+eig1(i); end
NEW=z*v(:,1:i)
18 W=100*eig1/sum(eig1) figure(1) pareto(W);
title('贡献率直方图');
L =(v') * diag(sqrt(eig1)); %方差贡献
Var = sum((L.^2)); %排序
Temp = [Var;1:length(Var)];
VarTemp = flipud(sortrows(Temp',1));
L = L(:,VarTemp(:,2));
Var = VarTemp(:,1);
j = 0; Sum = 0;
while Sum/sum(Var) <0.85 j= j +1;
Sum = Sum + Var(j);
end L_main = L(:,1:j);
H = sum((L_main.^2),2);
VarContr = 100 * Var/sum(Var);
figure(2) pareto(VarContr);
title('因子旋转前方差贡献度'); [L_New,psi,T,stats,F]=factoran(z,j,'rotate','varimax','scores','T homson');
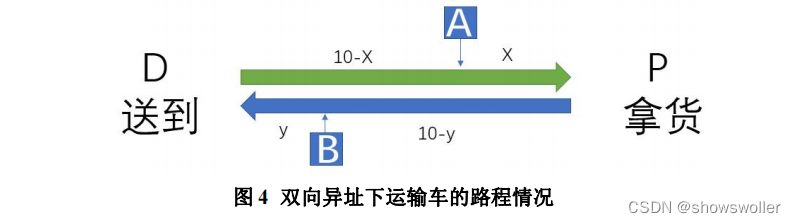
19 %新的共同度 H = sum((L_New.^2),2); 2：第二小问类似 但是不是换电站地址不同 需要设两个变量
83.3% + ?3 + 12 (10 − ?) % ≤ 90% 83.3% + ?2 + 1
3 (10 − ?) % ≤ 90%
0 ≤ ?, ? ≤ 10
2 + ? + 10 − ? + 220 = ? + 10 − ? + 220
求解代码如下
想具体了解可以关注后私信
from sympy import symbols,solve,linsolve
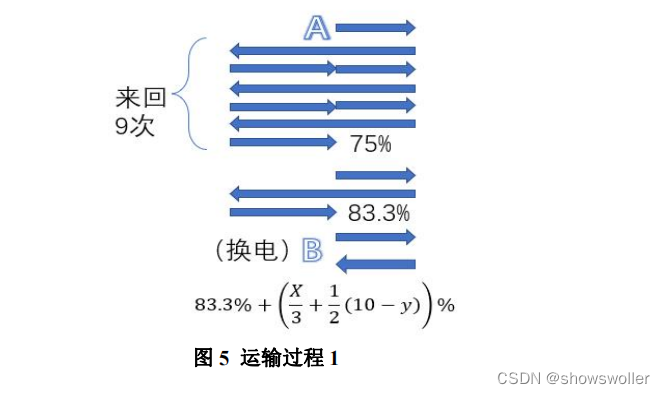
x,y=symbols('x y')
f1=0.833-0.9+0.01*x*(1/3)+0.05-0.01*y*0.5
print(solve([f1,f2]))
print(linsolve([f1,f2],(x,y)))3：第三问要自己去查一下相关材料的价格进行调度安排，以下是部分成本的价格
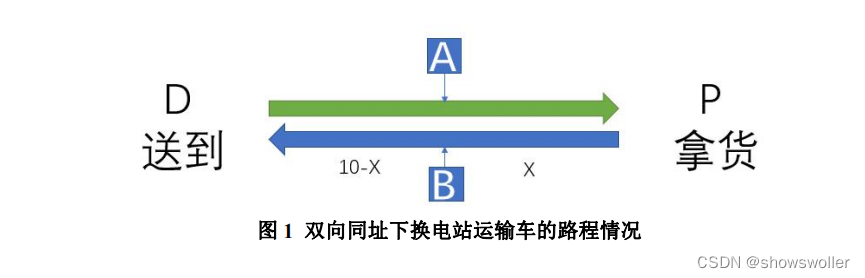
且该运输车的行驶情况与问题1类似。通过网上查询资料可知，一辆电动运输车的均价为约为9万元，则在118辆车所构成的一个循环中，所需要的车辆成本为1062万元。
经查询深圳电价统计局以及深圳市新能源电动汽车网，我们可发现该换电站选址处所使用的电为10千伏高供高计，且每个充电桩的功率7kw，而一个电池组充电时间约为3小时，则每个电池组的容量约为21kw.h，则一个循环所使用的电量为13608kw h
那么最后最低成本问题可以化简为电价最低，因为其他几项成本基本上可以固定，不会有太大的变化
考虑峰谷电价的影响，需知一单位千瓦时各阶段时的成本，即高峰时的价格，低谷时的价格。经中国南方电网查询，得
| 用电类别（每月） | 10千伏高供高计 | |||
| 峰 | 平 | 谷 | ||
| 大量工商业及其他用电 | 250KW H及以下 | 1.02756875 | 0.67506875 | 0.23105875 |
| 250KW H及以上 | 1.00758875 | 0.65506875 | 0.21106875 | |
再者，还需知峰谷电价各个阶段的时间，参考深圳市居民生活电价表里的峰谷电价阶段的各个时段：
表2 电价阶段时间表
| 电价阶段 | 时间 |
| 峰期 | 10:00-12:00,14:00-19:00 |
| 平期 | 8:00-10:00,12:00-14:00,19:00-24:00 |
| 谷期 | 0:00-8:00 |
为了保证3年结算周期投资运行成本最低，即应保证换电站的个数尽可能少，则我们可以选择建立一个类似问题一的双向同址的换电站，经查询，一个充换电站成本约为260万元。
第三问部分代码如下
from sympy import symbols,solve
totalElectricity=648*21
max=1.0075
average=0.655
min=0.211
averagecost=9*60/464*13608*average
print("低谷电价为",c3,"单位为万元")
print("车辆成本为",c4,"单位为万元")
print("换电设备成本为",c5,"单位为万元")
print("3年内总最低成本为",totalcost,"单位为万元")想具体了解可 关注后 私信我
4：第四问与第一问类似 但是要考虑多个拿货点 稍微复杂一点 要设多个未知量来表示多个拿货点到换电站之间的距离，但大题思路和第一问类似，以下以两个拿货点为例
对X1的情况进行讨论
当有多个拿货点的时候与此类似，当然两个拿货点之间最好至少要有一个换电站。
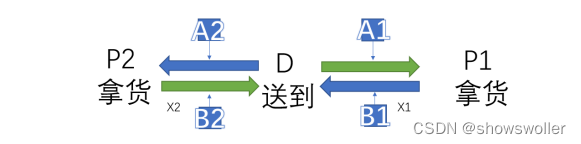
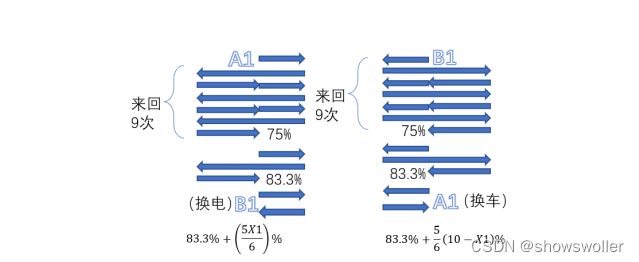
第四问部分代码如下
From sympy import symbols,solve,linsolve
X1=symbols('x1')
f1=(5/6)*x1*0.01+0.833-0.90
print(solve([f1<=0,f2<=0]))
想具体了解可以关注后私信
如想了解更多可以点赞关注收藏然后私信，这样系统提醒比较及时
